Henini M. Handbook of Self Assembled Semiconductor Nanostructures for Novel devices in Photonics and Electronics

Подождите немного. Документ загружается.

Cavity Quantum Electrodynamics with Semiconductor Quantum Dots 139

interface, while conﬁ nement in the vertical direction is provided by Bragg reﬂ ection. These cavi-

ties, obtained by etching a planar microcavity bounded by two Bragg reﬂ ectors, offer small cavity

volume and relatively high Q . Quality factors as high as 165 000 have been reported for 4 μ m

diameter III–V semiconductor pillars, which sustain modes with modal volume of the order of a

few tens of ( λ / n )

[31] . The main advantage of micropillars compared with other types of micro-

cavities is that light escapes very efﬁ ciently in the direction parallel to the pillar axis in a single-

lobe Gaussian-like pattern, which is well suited for light collection and coupling to optical ﬁ bres,

for example [32] .

Another example is the 2D photonic crystal cavity in a slab waveguide, consisting of a 2D

array of holes perforated through a thin membrane (see Fig. 4.2 right) [33] . In these cavities, the

photonic-band gap effect is used for strong light conﬁ nement in the transverse directions, and

total internal reﬂ ection at the air–slab interface ensures light conﬁ nement in the longitudinal

direction. The main advantage of such resonators is their relative ease of fabrication (since only

a thin slab of a few hundred nm thickness has to be pierced) associated with the wide variety

of possible 2D photonic crystal patterns (due to the inherent ﬂ exibility in hole shape, size, and

pattern). While many 2D photonic patterns (square lattice of holes, quasi-crystal-based arrange-

ment of holes, etc.) have been proposed and sometimes demonstrated, by far the most widely

studied arrangement is the hexagonal one. It has reasonably good band gaps for accessible values

of the index contrast and ﬁ lling factor. In these structures, the cavity is formed by the introduc-

tion of a point defect in the 2D photonic crystal: the in-plane photonic band gap, added to the

vertical waveguiding effect, leads to efﬁ cient 3D photon conﬁ nement even though no omnidirec-

tional band gap for photon propagation exists.

Different cavity geometries have been investigated, aimed at increasing Q factors while keep-

ing the modal volume as small as possible. The simplest geometry consists of removing a ﬁ nite

number of holes in a perfect array of holes. For instance, the Ln cavities are formed by a line of

n missing holes in a triangular array of holes. The so-called Hn cavities are formed by unperfo-

rated hexagons in a regular triangular photonic crystal with Γ M -type boundaries; these resona-

tors are described by the size n of their side in units of crystal period. Recently, several numerical

and experimental studies have shown that these microcavities are highly valuable candidates for

achieving high-quality factors with wavelength-sized modal volumes. By ﬁ nely tuning the holes’

position and/or radius at the cavity termination, it is possible to enhance the Q factor of these

resonators. This stronger light conﬁ nement results from the progressive increase of the reﬂ ec-

tivity at the cavity boundaries and the progressive decrease of the mode group velocity while

ﬁ nely tuning the arrangement of holes [34] . For instance, Q factors of 45 000 with ultra-small

volumes close to ( λ / n )

have been measured in an L3 microcavity etched in a Si membrane, by

slightly shifting the position of the holes surrounding the defect region [35] .

Figure 4.2 Images of different semiconductor cavity geometries, such as (left) micron-diameter GaAs microdisks,

(centre) AlGaAs/GaAs micropillars and (right) photonic crystal cavities etched on a 180 nm thick GaAs membrane

(Source: CNRS-LPN).

2 μm

1 μm

CH004-I046325.indd 139CH004-I046325.indd 139 7/1/2008 10:50:20 AM7/1/2008 10:50:20 AM

140 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

Another approach is the so-called double heterostructure cavity. The cavity is composed of a

line defect structure whose geometry (width, longitudinal periodicity, etc.) is locally changed, so

that a mode gap is created at the location of the geometry modulation: the band-edge frequency

of the fundamental line defect mode is lowered at the location of the geometry modulation,

which forms a well that can trap photons at appropriate frequencies. For instance, by changing

locally the width of a line defect, cavities with Q factors reaching 8  10

and a modal volume

of the order of (λ / n )

have been fabricated on Si-slab membranes [36] . Similarly, by changing

locally the longitudinal period of a line defect, cavities with Q factors reaching 10

and a modal

volume of the order of ( λ / n )

have been demonstrated on silicon slab waveguides [37, 38] . Such

resonators made of III–V semiconductor materials exhibit Q factors exceeding 10

[39, 40] .

4.3.2 The emitter: a single semiconductor quantum dot

In 1994, the emission of electron–hole pairs trapped in single quantum dots was experimentally

evidenced [41, 42] . These observations were almost simultaneously reported in two different sys-

tems. Marzin and co-workers reported on the micro-photoluminescence on single InAs quantum

dots. InAs quantum dots are formed during the epitaxial growth of an InAs quantum well in GaAs

barriers: because of the lattice parameter mismatch between the two materials, after the growth of

1.7 monolayers of InAs, strength relaxation leads to formation of 3D InAs islands with lateral size

around 20 nm and height around 3 nm [43] . After encapsulating the quantum dots with GaAs,

the InAs island forms an energy trap for electron–hole pairs in all directions. The gap difference

between InAs (0.41 eV) and GaAs (1.51 eV) is so large that the Coulomb interaction between the

electron and the hole is a perturbation as compared to the quantum conﬁ nement of the carrier

(around 10 meV as compared to a few 100 meV). To describe the ﬁ rst excited state of the quantum

dot, the term “ electron–hole pair ” is therefore more appropriate than the term “ exciton ” .

The other ﬁ rst demonstration of single quantum dot emission is observed in a very different

conﬁ nement regime [42] . The sample consists of a thin (10 monolayers) GaAs quantum well in

AlGaAs barriers. Even though molecular beam epitaxy is known to produce atomically smooth

interfaces, atomic roughness persists at the quantum–well interface. With standard growth con-

ditions, the roughness takes place on a small length scale, around 1–10 nm: an inhomogeneous

broadening of the 2D exciton line is observed both in micro- and macro-photoluminescence meas-

urements [44] . However, when performing growth interruption at the quantum–well interface

during the growth process, the roughness can take place on a larger length scale: between 10 and

200 nm [26, 42] . The lateral size of the defect is then larger than the Bohr radius of the 2D exci-

ton conﬁ ned in the quantum well so that a quasi 2D-exciton can be weakly localized in the inter-

face defect. These interface ﬂ uctuation quantum dots, often referred to as natural quantum dots,

present 0D density of states for the excitons, despited a small binding energy, around 15 meV [26] .

Both quantum dot types are promising emitters for solid-state quantum electrodynamics. The

discrete density of states, commonly leading to the “ macro-atom ” image, has been demonstrated

by observing single photon emission from both InAs [27, 28] and GaAs quantum dots [29] .

To demonstrate the Purcell effect, both InAs and GaAs quantum dots are equally interesting:

the typical emission linewidth (around a few tens of μ eV) and their small size as compared to

the emission wavelength make them ideal candidates to demonstrate the Purcell effect in a small

effective volume microcavity.

However, to reach an exciton–photon strong coupling regime, one needs to maximize the exci-

ton oscillator strength f . As discussed now, the oscillator strength of the exciton conﬁ ned in the

quantum dot can be much larger for natural quantum dots than for self-assembled single quan-

tum dots. For an interband transition, omitting numerical coefﬁ cients, the oscillator strenth is

given by [30] :

f u r u r r dr dr

cv Xeheh

∝

∫



Ψ (, )

(4.17)

where u

and u

are the rapidly varying part of the Bloch function for the electron and the hole

and

Xeh

rr(, )



is the excitonic envelope function.

CH004-I046325.indd 140CH004-I046325.indd 140 7/1/2008 10:50:21 AM7/1/2008 10:50:21 AM

Cavity Quantum Electrodynamics with Semiconductor Quantum Dots 141

For self-assembled InAs single quantum dots, the lateral conﬁ nement resulting from the quan-

tum conﬁ nement is of the order of or smaller than the 2D exciton Bohr radius of the exciton in

the wetting layer. In this case, one should consider independent quantization of electron and hole

in the plane rather than exciton conﬁ nement as a whole particle. The electron–hole pair wave

function then reads [12]:

Xeh e e h h e e h h

rr z z(, ) ( ) ( ) ( ) ( )



∝ ϕρϕρξ ξ

(4.18)

where



(resp.



) describes the in-plane wave function for the electron (resp. hole). The oscilla-

tor strength of the optical transition is then given by the overlap between the electron and hole

wave functions in all three direction of space:

fdzzdz

eh eh

∝

∫∫∫

ϕρϕρ ρ ξ ξ() () () ()



(4.19)

Equation 4.19 indicates that the oscillator strength of self-assembled InAs quantum dots hardly

depends on the precise geometry of the quantum dot. Indeed, the size dispersion among self-

assembled quantum dots is small as compared to the exciton Bohr radius, so that the electron–

hole overlap is very similar for various quantum dots. The typical calculated oscillator strength

for self-assembled InAs quantum dots emitting around 1.3 eV is around f  1 0 .

Consider now natural GaAs quantum dots. For quantum dots whose lateral size exceeds the

2D exciton Borh radius, one can conveniently separate the exciton centre of mass motion and

the electron–hole relative motion. The exciton wave function reads:

Xeh CM S ee h h

rr g R f z z(, ) ( ) () ( ) ( )





∝

loc 1

ρξ ξ

where

()



represents the in-plane relative motion and

CMloc

()



the localized centre of mass

movement. In GaAs natural quantum dots, the monolayer ﬂ uctuation at the quantum–well inter-

face localizes the exciton centre of mass on a scale roughly propotional to the lateral quantum dot

size (an experimental evidence of this phenomenon can be found in [9] ). As a result, for large GaAs

quantum dots, the oscillator strength is proportional to the area of the interface defect.

Different theoretical models demonstrated this dependence of the oscillator strength on the

quantum dot size in 1994 [12] . In 1999, Andreani and co-workers revisited this theoretical pre-

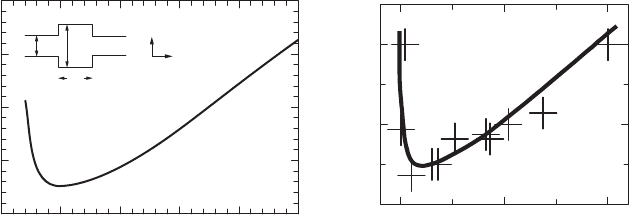
diction in the context of a cavity–quantum dot strong coupling regime. Figure 4.3 presents the

calculated oscillator strength for natural quantum dots formed at the interface of a 5 nm wide

GaAs quantum well with AlAs barriers. The calculated oscillator strength presents a minimum

value around the exciton 2D Bohr radius. This minimum is around f  5 0 , ﬁ ve times large than

for self-assembled InAs quantum dots. Most interesting is the calculated oscillator strength for

Figure 4.3 Left : Calculated oscillator strength for an exciton trapped in a monolayer ﬂ uctuation in a 4 nm wide

GaAs/AlAs quantum well as a function of the quantum dot radius from [10] . Right : Experimental measurement of

the oscillator strength for an exciton trapped in a monolayer ﬂ uctuation in a 3 nm wide GaAs/Al

0.3

0.7

As quantum

well [11] .

AlAs

GaAs

400

300

200

100

0 100 200 300 400 500

Oscillator strength

Defect radius (Å)

Oscillator strength

QD radius (A)

100

150

CH004-I046325.indd 141CH004-I046325.indd 141 7/1/2008 10:50:21 AM7/1/2008 10:50:21 AM

142 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

large quantum dot radius: it can reach values as large as f  300. These theoretical predictions

are quite promising: if one can ﬁ nd appropriate growth conditions, one can control the oscillator

strength of the quantum dot excitonic transition.

Experimental estimation of the strength of the optical transition of quantum dots has ﬁ rst been

obtained through time resolved photoluminescence measurements on quantum dot ensembles.

Provided that the capture time into the quantum dot is short [13] and non-radiative processes are

negligible, the decay time of the photoluminescence under non-resonant excitation gives a measure

of the exciton radiative lifetime. Measurements on InAs quantum dots demonstrate a radiative decay

time around 0.8–1.5 ns [14–16] corresponding to an oscillator strength between 9 and 15. Time

resolved PL on single InGaAs quantum dots demonstrated radiative decay time around 600–1300

ps [17, 18] . More recently, the absorption of a single quantum dot exciton line has been meas-

ured, giving access to both the homogeneous linewidth of the exciton transition and its oscillator

strength. To extract the small absorption contribution to the overall signal, Karrai et al. introduced

modulation of the excitonic transition through the Stark effect by applying a periodic electric ﬁ eld.

An oscillator strength of f  12 was also deduced from this technique. Measurement of GaAs natu-

ral quantum dots oscillator strength has also been obtained through differential absorption tech-

niques [19] . Oscillator strengths between 45 and 180 were reported using this technique. To prove

the dependence of the oscillator strength with the quantum dot lateral size, time resolved photo-

luminescence on single GaAs quantum dots was performed. The radiative decay time appeared to

vary from dot to dot between 100 ps and 230 ps corresponding to f  35–75. For each measure-

ment, the quantum dot lateral size was estimated through excitation of the photoluminescence

technique [20] . Doing so, the non-monotonous dependence of the oscillator strength with the

quantum dot radius was experimentally demonstrated (right part of Fig. 4.3 ) for quantum dot sizes

below 30 nm. Detailed analysis of the exciton and bi-exciton power dependence gives an estimation

of the capture time of carriers into the quantum dot (around 100 ps) [21] . For larger quantum dot

size, the expected radiative lifetime gets shorter than the capture time into the quantum dot so that

time resolved photoluminescence no longer gives access to the radiative decay of the transition.

However, when optimizing growth conditions, GaAs quantum dots as large as 100–200 nm can be

obtained [22] , for which oscillator strength around a few hundred are expected.

As we will discuss in Section 4.5, natural InGaAs quantum dots have also been used to demon-

strate the strong coupling regime. [23, 24] show that the quantum dot size strongly depends on

the In content of the quantum dot layer. For In content around 30%, large elongated quantum

dots are formed, with typical sizes of 30  100 nm. The oscillator strength for these quantum

dots is estimated to be around 50. Finally, another option could be explored to develop fast radia-

tive quantum dots as demonstrated in [25] . Large InAs self-assembled quantum dots emitting

around 0.95 eV (1.3 μ m) are grown by molecular beam epitaxy. A large quantum dot size leads

to f  30. To increase further the oscillator strengh, rapid thermal annealing at high temperature

is used: In/Ga interdiffusion blue shifts the quantum dot emission and increases the quantum dot

size in all directions. Oscillator strengths around f  100 could be obtained with this technique.

In the present section, we have discussed the need to insert large oscillator strength quantum

dots in ultimate nanocavities to demonstrate a strong coupling regime. Note that fast radiative

quantum dots are also of great interest for the generation of indistinguishable photons as well

as entangled photon pairs. Section 4.7.1 reports on the demonstration of indistinguishable pho-

tons using the Purcell effect to limit the dephasing processes during the quantum dot emission.

Natural, fast, radiative quantum dots could also be promising candidates for such applications.

4.4 The weak coupling regime

4.4.1 Spontaneous emission inhibition

The conditions for observing spontaneous emission suppression are quite stringent. In order to

determine the requirements for implementing such an effect, let’s turn again to equation 4.11.

The ﬁ rst term, related to emission into the cavity mode, vanishes as the quantum dot fundamental

transition line is far detuned from the cavity resonance or if the quantum dot is located at a node

CH004-I046325.indd 142CH004-I046325.indd 142 7/1/2008 10:50:22 AM7/1/2008 10:50:22 AM

Cavity Quantum Electrodynamics with Semiconductor Quantum Dots 143

of the cavity ﬁ eld. The second term Γ

leak

/ Γ

describes the possible decay due to emission into

residual modes. Generally, this latter contribution to spontaneous emission decay precludes the

implementation of spontaneous emission suppression: the conﬁ ned optical modes in most reso-

nators are superimposed on a quasi-continuum of “ leaky ” photon modes along the cavity, so that

the off-resonance emission is little changed from its value in a homogeneous medium. However,

it becomes possible to reduce or even suppress the contribution of this residual decay channel by

use of 3D photonic crystal [54] . In these structures, the local density of optical states in the phot-

onic crystal for emission inside the photonic band gap is reduced or even vanishes, removing also

any additional decay channel within this spectral range. Therefore, for quantum dots emitting

within the photonic band gap, suppression of spontaneous emission is made possible. However,

as mentioned above, the fabrication of photonic crystals with full three-dimensional band gap is

quite severe, even if the recent progress in the ﬁ eld is spectacular.

Hopefully, partial inhibition of spontaneous emission can be observed by use of 2D hexagonal

photonic crystals etched on a suspended membrane, due to their “ partial ” TE band gap. For struc-

tures with adjusted geometries (whose parameters are the membrane thickness, holes radius and

lattice spacing), such photonic crystal membranes exhibit a wide band gap for TE guided modes

(i.e. modes with an electric ﬁ eld in the central plane of the slab pointing along the membrane),

but no gap for TM modes (i.e. modes with an electric ﬁ eld pointing along the holes axis) [33] .

Consider now a single dipole located vertically in the middle of the membrane. For dipoles ori-

entated perpendicular to the membrane and therefore only coupled to TM modes, no gap in the

emission rate can be observed but only a weak dependence on frequency, as expected from the

absence of a 2D band gap for the TM-guided modes of the membrane. Conversely, for dipole ori-

entations in the plane of the membrane and therefore only coupled to TE modes, a deep inhibition

in the spontaneous emission rate should occur for emission in the photonic band gap. This latter

effect has been demonstrated by incorporating single self-assembled InAs/GaAs quantum dots in

H1 and L3 photonic crystal slab cavities etched on a GaAs suspended membrane [70–73] . The

dipole orientation of the fundamental transition of these emitters is perpendicular to the holes ’

axis [74] , so that the emitter couples only to the TE modes of the photonic crystal: The exciton

“ feels ” the TE band gap but does not “ see ” the absence of TM band gap, enabling therefore the

implementation of spontaneous emission suppression. Indeed, time resolved photoluminescence

experiments on off-resonant quantum dots in such cavities indicate up to ﬁ ve-fold rate quenching

due to the reduction of the local photon density of states in the photonic band gap [70] .

4.4.2 Spontaneous emission acceleration

The quantum analysis of spontaneous emission based on Fermi’s golden rule asserts that the

largest enhancement of spontaneous emission rate of an emitting dipole is achieved if the dipole

is on resonance spatially and spectrally with a high- Q / V single cavity mode and is pointing along

the cavity electric ﬁ eld (see Eq. 4.11). The amplitude of this acceleration will be strongly depend-

ent on the dipole orientation and the spatial and spectral matching of the emitter dipole with

respect to the cavity ﬁ eld.

As mentioned above, progress in micro fabrication techniques has allowed a three-dimen-

sional engineering of the refractive index on the wavelength scale and a rich diversiﬁ cation of

the microcavity designs. For instance, micropost resonators, photonic disks and 2D photonic

band gap slab microcavities sustain a discrete set of resonant modes with high- Q / V factors and

have the potential to display a signiﬁ cant Purcell effect, provided a convenient emitter is used.

Self-assembled InAs quantum dots constitute an appealing class of light emitters in this respect.

Owing to their discrete density of electronic states, individual quantum dots exhibit a single, very

narrow emission line under weak excitation conditions, which allows implementing signiﬁ cant

CQED effects in high- F

microcavities. However, the random nucleation position and size (and

consequently emission wavelength) of such nano-emitters present a challenge to the efﬁ cient

spectral and spatial coupling of the dot to the cavity mode. It should be repeated that the spon-

taneous emission rate of a given quantum dot into a cavity mode depends on its location and

emission wavelength, which govern, respectively, the amplitude of the electric ﬁ eld it feels and

the density of modes to which it is coupled.

CH004-I046325.indd 143CH004-I046325.indd 143 7/1/2008 10:50:22 AM7/1/2008 10:50:22 AM

144 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

In their pioneering work [7] , J.-M. Gérard et al. used ensembles of InAs/GaAs self-assembled

quantum dots embedded in GaAs/AlGaAs micropost cavities. A spontaneous emission rate

enhancement by a factor of up to 5 was selectively observed for the quantum dots which were

on resonance with one-cavity mode. The discrepancy between the expected Purcell factor (  30)

and the observed enhancement results from a statistical averaging of the effect over all resonant

dots of random spatial and spectral distributions with respect to the cavity mode. More recently,

similar experiments have been carried out using only one self-assembled InAs/GaAs quantum

dot. In this context, it should be possible to fully beneﬁ t from the Purcell effect, providing exact

resonance energy and location of the dot with respect to the cavity mode.

The condition of spatial resonance is a real challenge, even if recent progress is quite promising

in this ﬁ eld (through localization of the dot nucleation site or localization of the cavity around

the randomly located dot, for instance – see paragraph 4.6.1). Therefore, most experiments per-

formed up to now rely on a random spatial overlap between the individual quantum dot and the

cavity mode and the spatial resonance condition is partially statistically fulﬁ lled while scanning

a large number of processed cavities embedding dilute arrays of dots.

The spectral resonance condition can be more easily satisﬁ ed. Two strategies can be used: tun-

ing the cavity mode resonance to the energy of the fundamental transition of the dot or tuning

the energy of the fundamental transition of the dot to the cavity mode resonance. This ﬁ rst

approach can easily be implemented in some cavity geometries, mainly photonic crystal slab cav-

ities whose resonance is tuned through successive cycles of oxidation and wet etching of the slab

membrane [75, 76] . Another technique consists of varying, on the same sample, the cavities ’

geometry (for example, the diameters for micropost resonators) in order to shift spectrally the

resonance conditions from one cavity to another on the same sample and cover a large spectral

range. The second approach, consisting of spectral tuning of the dot transition to the cavity mode,

exploits either the spectral dispersion of the dots by using dots of different sizes or the spectral

tuning of the fundamental transition wavelength of the quantum dot as a function of tempera-

ture: when increasing the temperature from 5 to 50 K, the dot exciton wavelength red shifts by

about 2 nm while the resonant wavelength of the mode red shifts by only less than 1 nm.The two

can then be brought into resonance at a precise temperature (see Fig. 4.4 left). This effect has been

successfully implemented in many different cavity geometries: microdisk [77] , micropillar [78] ,

and 2D photonic crystal slab cavity [73] .



5.0

Spontaneous emission

enhancement F

Cavity detuning (in Å)

2.5

0.0

2.5

5.0

Quantum dot exciton

Cavity mode

919.5

920.0

920.5

921.0

921.5

Wavelength (nm)

Temperature (K)

0 1020304050

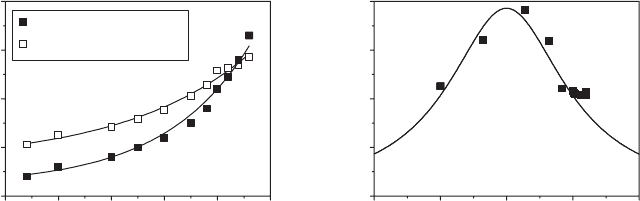
Figure 4.4 Left : Spectral resonance matching of a single InAs quantum dot exciton to a micropillar cavity mode via

temperature tuning, for an InAs/GaAs dot embedded in a 400 nm diameter GaAs/AlGaAs micropost with Q factor of

1600. Right: Amplitude of the spontaneous emission enhancement F as a function of spectral detuning, ﬁ tted by a

Lorentzian.

While combining these different strategies to couple a single dot to a cavity mode, signiﬁ cant

Purcell effects on single dot have been recently observed at low temperature (  50 K). Direct

measurements of spontaneous emission decay on resonant single quantum dots indicate an

enhancement of the spontaneous emission dynamics of the order of a few units either in micro-

disks ( F  6 [77] ), micropillars ( F  10 [79] ) or photonic crystal slab resonators ( F  10 [70,

CH004-I046325.indd 144CH004-I046325.indd 144 7/1/2008 10:50:22 AM7/1/2008 10:50:22 AM

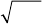
Cavity Quantum Electrodynamics with Semiconductor Quantum Dots 145

73] ). The resonant character of this effect can be highlighted when tuning the dot wavelength

with respect to the cavity resonance through sample temperature increase, for example: when

the exciton wavelength is slightly detuned from the cavity spectral resonance, the amplitude of

the spontaneous emission rate enhancement decreases (see Fig. 4.4 right).

4.5 The strong coupling regime

To reach a strong coupling regime, one needs not only to develop cavities with high quality factor

and small effective volume: one needs to maximize the quantity

QfV/

(see Eq. 4.16). In

2001, Gérard estimated the possibility of reaching a strong coupling regime using one of the

state of the art existing microcavities using self-assembled InAs quantum dots [80] . The authors

calculated that the limit between weak and strong coupling regime could be reached using either

microdisk microcavities or photonic crystal microcavities. To achieve light–matter entanglement,

one needed either to improve the cavity performances or to use larger oscillator strength quan-

tum dots. Three years later, the strong coupling regime was demonstrated in three groups, with

different strategies both concerning the quantum dot and the cavity system [81, 82, 22] . In these

three demonstrations, the same experimental techniques were used to demonstrate the strong

coupling regime. In the following, we detail the demonstration of the strong coupling regime we

obtained using GaAs quantum dots inserted in microdisk microcavities, which sustain whispering

gallery modes (WGM). We then present the other demonstrations and discuss the ﬁ gure of merit

for the three systems.

4.5. 1 First demonstrations of strong coupling regime

A way to demonstrate a strong coupling regime is to bring an exciton transition in resonance

with the cavity mode transition. At resonance, anticrossing between the two lines is a signature

of light–matter entanglement. Micro-photoluminescence is an efﬁ cient tool to monitor an exci-

tonic transition energy. However, one could wonder if it is also an efﬁ cient tool to monitor the

energy of an optical resonance. Indeed, optical mode energies are usually identiﬁ ed by insert-

ing a large density of quantum dots providing a broadband emission source inside the microcav-

ity. The quantum dot emission is then ﬁ ltered by the cavity so that optical mode energies appear

as well as identiﬁ ed lines on the photoluminescence spectrum [83, 84] . When only a few dots

are embedded inside the microcavity, one might wonder how to identify the mode resonance.

For high-quality factor microcavities ( Q  10–20 000), micro-photoluminescence experiments

show that most of the time an emission line is observed at the energy of the optical mode. The

origin of this line has not been fully understood up to now. The emission is referred to as a “ back-

ground signal ” ﬁ ltered by the cavity mode. Yet, some recent experimental studies indicate that

the emission ﬁ ltered by the cavity mode is correlated to emission from single dots even though

cavity mode exciton detuning is large [85, 86] .

For a typical quality factor of 15 000, the photon mode linewidth is around 100 μ eV. When

studying the emission from a single microcavity, one needs to ﬁ nd a way to identify the exciton

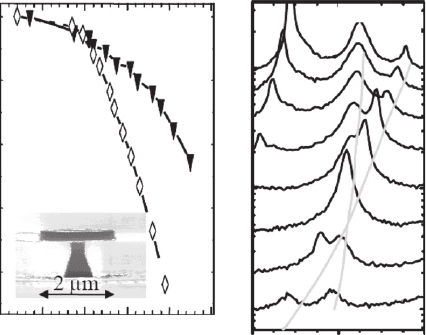
lines and the “ photon ” lines. Figure 4.5 shows typical spectra observed on a single microdisk

embedding GaAs natural quantum dots. Several lines are observed on the spectrum with simi-

lar linewidths. To identify the origin of the lines, temperature is increased. Figure 4.5a presents

the absolute spectral shifts for a quantum dot exciton (quantum dot X) and a whispering gallery

mode (WGM) resonance. When increasing temperature, both the exciton and the WGM energy

decrease. The ﬁ rst one varies like the gap of bulk GaAs. The second decreases due to increase

of the AlGaAs refractive index with temperature. These characteristic spectral behaviours are

observed for every optical mode and quantum dot exciton on every microdisk so that varying

temperature allows identifying exciton or optical mode origin of the emission lines. Finally, tem-

perature tuning can be used to bring an exciton resonance into the cavity mode resonance.

Considering the spectral shift with temperature for each line observed in Fig. 4.5b , one can

attribute the two highest energy lines to the emission of a small background within a whisper-

ing gallery mode and to the radiative recombination of a quantum dot exciton (quantum dot X).

CH004-I046325.indd 145CH004-I046325.indd 145 7/1/2008 10:50:22 AM7/1/2008 10:50:22 AM

146 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

When increasing temperature, a crossing of the two lines is observed at 37 K: the system is in

the weak coupling regime. However, for a 2 μ m diameter microdisk the mode effective volume

is around V  0 . 0 7 μ m

. Considering a quantum dot with an excitonic oscillator strength of

f  100 placed at an antinode, the system is expected to be in the strong coupling regime, with

a Rabi splitting of 400 μ eV. The observation of weak coupling regime is the signature that this

quantum dot is most probably not positioned at a maximum of the electromagnetic ﬁ eld, which

is the last condition required to observe a strong coupling regime.

To ﬁ nd a quantum dot exciton in both spectral and spatial resonance with the optical mode,

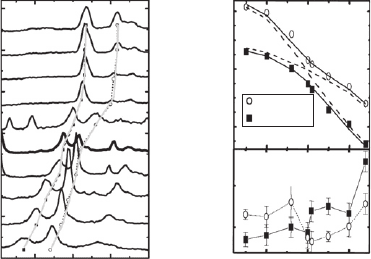
many individual microcavities are studied. Figure 4.6a presents similar measurements per-

formed on another 2 μ m microdisk. Mainly, two lines are observed at each temperature. When

increasing temperature from 4 K up to 30 K, the upper line shifts more than the lower line. This

shows that the upper line can be assigned to a quantum dot exciton emission, and the lower line

to an emission within a WGM. Yet, when increasing further temperature, the observed spectral

shifts differ both from the one of an exciton and an optical mode: we observe an anti-crossing

between the two lines, spectral signature of the strong coupling regime. The eigenstates of the

system are not the exciton and photon states any more, but two exciton–photon mixed states,

whose mixing depends on temperature. Figure 4.6 presents the emission energy of the upper and

lower lines as a function of temperature. The dashed line indicates the spectral shift of weakly

coupled exciton and WGM lines. The anti-crossing takes place at 30 K, where the energy separa-

tion between the upper and lower line reaches the minimum value of 400 μ eV. The solid lines

present the calculated coupled mode energy, considering the energy of the uncoupled WGM and

quantum dot exciton mode and a Rabi splitting of 400 μ eV. From the experimental Rabi splitting,

with an effective volume of V  0 . 0 7 μ m

, an exciton oscillator strength of f  100 is deduced.

This value is a minimum value since there is probably a spatial mismatch between the quantum

dot and the optical mode antinode.

500

1000

1500

2000

Spectral shift (μeV)

01020304050

Temperature (K)

1660 1662 1664

Energy (meV)

QDX

WGM

(a) (b)

49 K

43 K

37 K

33 K

29 K

25 K

20 K

5 K

PL intensity (arb. u.)

Figure 4.5 (a) Absolute spectral shift of the quantum dot exciton emission energy (diamonds) and of the WGM

energy (triangles) as a function of temperature. Inset : SEM image of a 2 μ m microdisk. (b) Photoluminescence

spectra under non-resonant continuous excitation for a particular microdisk of sample 2, for various temperatures.

Figure 4.6c summarizes the measured linewidths of the upper and lower lines as a function of

temperature. At low temperature (5–25 K), the minimum value of the photon-like (lower line)

linewidth is 140 μ eV ( Q  12000). The emission linewidth of the exciton-like upper line below

resonance is around 280 μ eV. At resonance, because of the half-exciton/half-photon nature of

the eigenstates, their emission lines present the same linewidth (180 μ eV), close to the expected

average of 210 μ eV.

CH004-I046325.indd 146CH004-I046325.indd 146 7/1/2008 10:50:22 AM7/1/2008 10:50:22 AM

Cavity Quantum Electrodynamics with Semiconductor Quantum Dots 147

The same procedure based on spectral tuning through temperature has been used for the ﬁ rst

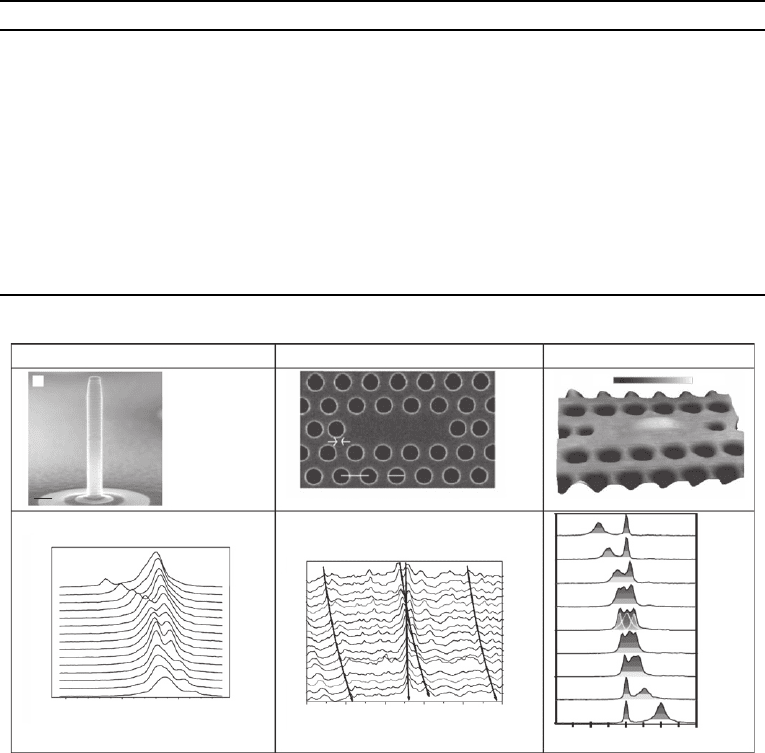
demonstrations of the strong coupling regime ( Fig. 4.7 ). Reithmaier and co-workers have cho-

sen to insert “ natural ” InGaAs quantum dots in micropillar microcavities [81] . The success of

this demonstration relies on two remarkable achievements. On the one hand, whereas the quality

factor of micropillar microcavities is known to decrease strongly for diameters below 2 μ m [23] ,

Reithmaier has succeeded in increasing signiﬁ cantly this quality factor both by achieving quality

factors over 100 000 for the planar cavity and improving the etching process [31] . On the

other hand, a new type of quantum dot was developed leading to oscillator strength around 50.

Poloczek and co-workers [24] have studied the inﬂ uence of In content and strength on the growth

of InGaAs quantum dots. For an indium content around 36%, large highly anisotropic quantum

dots appear with a typical size of 100 nm  20 nm presenting f  50. The strong coupling regime

was ﬁ rst reported in this system using a 1.5 μ m diameter with Q  8000 and effective volume of

V  0 . 3 μ m

. This relatively large effective volume is compensated by the large oscillator strength of

the quantum dot so that a Rabi splitting at a resonance of 170 μ eV was observed.

Finally, the strong coupling regime was demonstrated using photonic crystal microcavities.

The strong coupling regime has been evidenced twice by inserting InAs self-assembled quantum

dots in modiﬁ ed L3-type optical microcavities [82, 87] . Despite the small oscillator strength of

InAs quantum dots, the strong coupling regime is reached due to the small effective volume of

these cavities V  0.04 μ m

Note that in the demonstration reported by Henessy and co-workers [87] , a third line is

observed together with the Rabi doublet. The appearance of this line is most probably due to spec-

tral wandering of the quantum dot emission. The quantum dot emission can exhibit both exciton

and charged exciton line, indicating that the capture of carrier into the quantum dot can be inde-

pendent of electrons and holes. If the exciton–photon system is in the strong coupling regime,

the charged exciton is detuned so that when charged excitons are trapped in the quantum dot,

the energy of the optical mode is hardly modiﬁ ed.

Finally, we would like to mention another demonstration of strong coupling regime using a

solid-state emitter, namely, CdSe nanorods inserted at the surface of a silicon microsphere.

Despite the large effective volume of the cavity, a strong coupling regime is reached using large

oscillator strength nanorods. The tuning between the cavity mode and the exciton emission is

observed through spectral wandering of the line, as dominant effect for nanocrystals [88] .

The ﬁ gure of merit for the strong coupling regime is the Rabi splitting over linewidth ratio at

resonance

4g

/( )γγ

. Indeed, this ratio is a measure of the number of Rabi oscillations the

system can undergo before the photon escapes outside the cavity or the exciton is scattered to

a higher energy state. A summary of the four strong coupling realizations is presented below.

A maximum ﬁ gure of merit of 2 has been demonstrated up to now as compared to 5 for single

atoms trapped in an optical microcavity [89] .

1668

1666 1667 1668 1669

1667

1666

400

200

20 30 40

Temperature (K)

PL intensity (arb. u.)

Ener

y (meV)

FWHM ( eV) Energy ( eV)

WGM

QDX

4 K

10 K

15 K

20 K

26 K

30 K

31 K

35 K

40 K

44 K

(a)

(b)

Upperline

Lowerline

Figure 4.6 (a) Photoluminescence spectra under non-resonant continuous excitation for a particular microdisk for

various temperatures. (b): Symbols: emission energy of the upper and lower lines as a function of temperature. Line:

spectral shift of a quantum dot X and WGM. Continuous: calculated energy of the two coupled states. (c) Emission

linewidth of the lower (circles) and upper (squares) lines as a function of temperature.

CH004-I046325.indd 147CH004-I046325.indd 147 7/1/2008 10:50:23 AM7/1/2008 10:50:23 AM

148 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

[81] [82] [22] [87]

Cavity Micropillar Photonic crystal

slab

Microdisk Photonic crystal

slab

Energy (eV) 1.32 1.05 1.66 1.32

Q 7350 6000 12 000 13 300

V ( μ m

)

0.3 0.04 0.07

 0.04

Quantum dot In

0.3

0.7

As InAs GaAs InAs

Size

30  100 nm

 2 5 n m  4 4 n m

–

f 50 10 100

 10

140 μ eV 140 μ eV 180 μ eV 35 μ eV

Rabi splitting

2 g

140 μ eV 170 μ eV 410 μ eV 150 μ eV

2g/

1 1.3 2.2 2

4.5.2 Some perspectives

We shall discuss below some quantum information processes based on the strongly coupled dot–

cavity system (section 4.7.5) as well as the technological challenges that need to be addressed

(section 4.6). Naturally, the physics of a strong coupling regime in a solid-state system has yet to

be explored, as it has been investigated in atom-based systems.

One signature of the light–matter entanglement should be observed by performing crossed

correlation measurement on the Rabi doublet. To perform such an experiment, the Rabi dou-

blet over linewidth ratio will have to be signiﬁ cantly increased. However, recently, photon cross-

correlation measurement on an exciton line and a photon line far from resonance show clear

antibunching [87] . This ﬁ rst experimental study of the physics of a strong coupling regime

reports interesting yet little understood correlation measurements.

Because of the fermionic nature of the electron–hole pairs trapped in a quantum dot, the

Jaynes–Cumming ladder should be observed when more than one photon is introduced in the

cavity. Such observations have been reported for a small number of photons in an atom–cavity

system [90] and could be implemented with quantum dots.

(81) (82) (87)

1μm

a 0

7 nm

0.23 nm

0.14 nm

0.07 nm

0.01 nm

0.03 nm

0.07 nm

0.15 nm

0.30 nm

0.3

0.3 0.601

0.02 nm

  

(nm)

PL intensity (arbitarary units)

1,180 1,181 1,182 1,183 1,184 1,185

Wavelength (nm)

Energy (meV)

1322.5 1323.0 1323.5

5 K

21 K

30 K

Intensity (arbitrary units)

Figure 4.7 Three demonstrations of strong coupling regime. Top : SEM images (left and middle) and AFM image of

the cavity system. Bottom : experimentally measured anti-crossing between the exciton and photon lines.

CH004-I046325.indd 148CH004-I046325.indd 148 7/1/2008 10:50:23 AM7/1/2008 10:50:23 AM