Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

10 PFG NMR Studies of Anomalous Diﬀusion 425

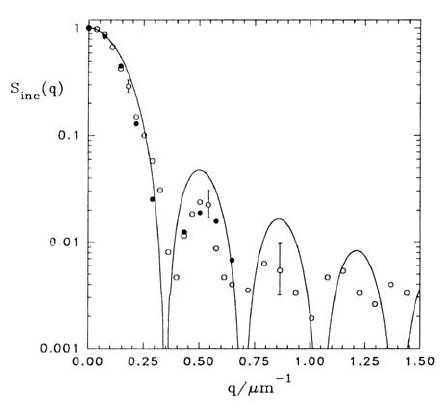
Fig. 10.2. Spin-echo attenuation of n-heptane diﬀusing in the space between par-

allel glass plates with the normal parallel to the direction of the ﬁeld gradient. The

curve is the diﬀraction pattern of a single slit of 18 µm width [26].

where we have used P (z

, ∞)=p(z

). Equation (10.19) corresponds to

the elastic incoherent structure factor (EISF) of QENS ((3.18) of Chap. 3).

F (q) is the Fourier transform of the conﬁning geometry p(z). The expression

in the last line of (10.19) is known as the form factor in scattering theory. It

describes the diﬀraction pattern of the scattering geometry p(z). This analogy

of PFG NMR with a scattering experiment was nicely demonstrated in [26],

cf. Fig. 10.2, where the echo attenuation of n-heptane diﬀusing in the space

between parallel glass plates was compared with the diﬀraction pattern of

the slit.

10.3.4 Experimental Conditions

The measurement of the spin-echo attenuation Ψ as a function of the ﬁeld gra-

dient pulse programme clearly implies the existence of a measurable NMR

signal. Therefore, the molecules under study must contain “NMR active”

atoms, i.e. nuclei with a non-vanishing magnetogyric ratio, which have to

occur with a suﬃciently large density. For hydrogen, e.g., which oﬀers the

best measuring conditions with respect to both the minimum number of dif-

fusants and minimum displacements, typical minimum concentrations are of

the order of one hydrogen nucleus per 10 nm

which corresponds to about 0.1

moles per litre. Hence, PFG NMR is not very appropriate for studying the

diﬀusivities of species, which are only present in minor concentration. In prin-

426 J¨org K¨arger and Frank Stallmach

ciple, clearly, with a suﬃciently large number of acquisitions, even at much

smaller concentrations NMR signals may be generated. For the measurement

of small diﬀusivities, however, such a procedure is far more subjected to the

risk that signal attenuation is due to a mismatch between the ﬁeld gradient

pulses or mechanical instabilities rather than to diﬀusion. Diﬀusivity data

determined under such conditions may dramatically exceed the real values.

We shall return to this point at the end of this section.

The measuring conditions are furthermore determined by the nuclear

magnetic relaxation times (cf. Sect. 9.3 in Chap. 9). In the above introduced

primary or Hahn-echo experiment (

– τ – π – τ – echo), the observation time

is essentially limited by the transverse relaxation time T

. If the longitudinal

relaxation time T

is notably larger than T

, the observation time may be

further enhanced by applying the stimulated echo (

– τ

–

– τ

–

– τ

–

echo) where the ﬁeld gradient pulses are applied during the two time intervals

of duration τ

. As in the case of the primary echo, signal attenuation during

these two time intervals occurs with the time constant T

, while during the

time interval τ

signal attenuation is governed by T

. Typical values of T

and T

and hence of the observation times in diﬀusion studies by PFG NMR

are of the order of milliseconds to seconds.

In deriving (10.14, 10.15) and (10.18) we have presumed that during the

ﬁeld gradient pulses the spins assume well-deﬁned positions. Such an as-

sumption is clearly only acceptable if molecular displacements during the

ﬁeld gradient pulses are negligibly small in comparison with those between

the pulses. In the case of normal diﬀusion it may be shown [6–9] that these

relations may be maintained also for ﬁeld gradient pulses of ﬁnite duration

by simply replacing the quantitiy ∆ by an “eﬀective” observation time ∆−

The PFG NMR method works under the supposition that the values of

δg for the ﬁrst and second ﬁeld gradient pulses are identical. Any diﬀerence

has the same eﬀect as translational motion of the molecules under study,

leading to a signal attenuation. The correct application of PFG NMR there-

fore necessitates extremely stable gradient currents, which generate the ﬁeld

gradient pulses within suitably structured ﬁeld gradient coils [5–8]. Likewise

high mechanical stability of both the ﬁeld gradient coils and the sample must

be ensured, since any movement of the sample with respect to the coils would

also lead to diﬀerences in the local ﬁeld at the instants of the ﬁrst and second

ﬁeld gradient pulses and to an additional attenuation of the spin echo.

Intrinsic diﬀerences in the magnetic susceptibility of heterogeneous sam-

ples give rise to internal ﬁeld gradients, which are superimposed upon the ex-

ternally applied ones. While under the inﬂuence of the modest external mag-

netic ﬁelds produced by iron magnets, for a number of important adsorbate-

adsorbent systems such as zeolites these superpositions could be shown to be

of no disturbing inﬂuence if only suﬃciently large pulse gradient intensities

are applied [27], in PFG NMR diﬀusion measurements with superconducting

magnets such disturbing inﬂuences have to be considered. As a most eﬀec-

10 PFG NMR Studies of Anomalous Diﬀusion 427

tive possibility to circumvent such diﬃculties, the application of pairs of ﬁeld

gradient pulses with alternating signs (±g) separated by appropriate rf (viz.

π) pulses has been suggested [28,29].

Methodical development in PFG NMR is focussed on the generation of

extremely large ﬁeld gradient pulses [21–25]. The diﬃculties due to the re-

quirement of perfect matching between the two ﬁeld gradient pulses may be

circumvented by applying the stimulated spin echo under the inﬂuence of a

strong constant ﬁeld gradient [8, 30–32], which is provided by the stray ﬁeld

of the superconducting magnet (“stray ﬁeld gradient” (SFG) NMR). The in-

tensity of the stimulated echo is inﬂuenced by the ﬁeld gradient only during

the two time intervals of duration τ

. These are exactly those time intervals

during which – as we have seen above – also the pulsed ﬁeld gradients are

applied. Therefore, signal attenuation is described by the same equations as

in the case of PFG NMR with the pulse width δ replaced by τ

and the

observation time ∆ being equal to τ

+ τ

. By this technique, presently the

largest ﬁeld gradient “amplitudes” (up to 185 T/m) may be achieved [33].

In comparison with PFG NMR, however, the signal-to-noise ratio is dramat-

ically reduced since only a slice of the sample of thickness of the order of

0.1 mm is at resonance, so that much larger acquisition times are inevitable.

These are, however, much easier to be accomplished since the requirement

of identical ﬁeld gradient “pulses” is automatically fulﬁlled in this technique.

A severe disadvantage of SFG NMR is the fact that the large constant mag-

netic ﬁeld gradient excludes the possibility of Fourier transform PFG NMR

for multicomponent diﬀusion studies [34, 35]. SFG NMR measurements are

additionally complicated by the fact that by varying the “width” of the ﬁeld

gradient “pulses” the signal is aﬀected by both diﬀusion and transverse nu-

clear magnetic relaxation.

10.4 PFG NMR Diﬀusion Studies in Regular Pore

Networks

At a ﬁrst glance, regular pore networks do not seem to be a suitable system

for studying anomalous diﬀusion. There are, however, a number of reasons,

which justify the inclusion of this section in the present chapter. Regular

pore networks of rather diverse nature are provided by the zeolites [3,36,37].

Originally, zeolites have only been known as minerals. They are microporous,

crystalline aluminosilicates. Starting in the ﬁfties of the last century, how-

ever, also artiﬁcial zeolites have been synthesized. As an example, Fig. 23.5

of Chap. 23 shows the structure of a zeolite of type LTA – in short – an A-type

zeolite. The last few years have been characterized by an explosion of new

zeolite structure types [37]. Most of them have no natural counterpart. The

great interest in zeolites results from their potential as selective adsorbents,

catalysts and cation exchangers, leading to proﬁts of the order of hundreds

of billions of dollars worldwide attained per year by their production and

428 J¨org K¨arger and Frank Stallmach

application. However, zeolites have also become an attractive object of fun-

damental research. Owing to their well-deﬁned structure and the diversity of

their nature, zeolites have proved to be ideal model systems, in particular

for studying the interaction of molecules with solid surfaces as exempliﬁed in

Pfeifer’s classical survey [38]. Thus, zeolites have also become a most attrac-

tive host system for studying molecular diﬀusion [3]. They have in particular

turned out to be an ideal system for demonstrating the versatility of PFG

NMR. This possibility and the numerous correlations with Chap. 23 moti-

vated us to include this section into a chapter about anomalous diﬀusion.

Moreover, we shall also learn that under certain conditions even a regular

zeolite pore system may give rise to anomalous diﬀusion.

10.4.1 The Diﬀerent Regimes of Diﬀusion Measurement

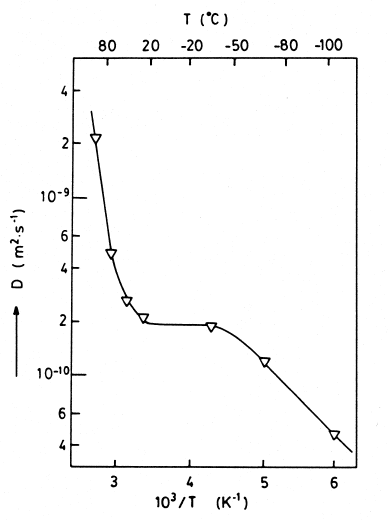
As an example, Fig. 10.3 shows an Arrhenius plot of the eﬀective diﬀusivity

(cf. (10.9)) as determined by PFG NMR for n-hexane in a sample of NaX

zeolite crystallites of mean diameter 4 µm for an observation time of 4 ms. One

may clearly distinguish between three diﬀerent regimes. For temperatures

below about 220 K, the diﬀusion paths are suﬃciently small in comparison

with the crystallite diameters, so that the eﬀective diﬀusivity is exclusively

Fig. 10.3. Temperature de-

pendence of the eﬀective self-

diﬀusivity for n-hexane in a

sample of NaX zeolite crystals

of mean diameter 4 µmatasor-

bate concentration of 20 mg/g

and observation time 4 ms [3].

10 PFG NMR Studies of Anomalous Diﬀusion 429

determined by intracrystalline diﬀusion. The situation is the same as in the

propagator representation of Fig. 10.1 (a) at 153 K. This is the regime of PFG

NMR measurements which shall be exclusively considered in the subsequent

Sects. 10.4.2 to 10.4.5. In the subsequent temperature range up to about

290 K, the diﬀusion paths are limited by the extensions of the crystallites

(situation as in Fig. 10.1 (b) at 153 K). Under the assumption that (i) the

conﬁnement is perfect and that (ii) the observation time is much larger than

the mean diﬀusion time over a distance of the order of the crystallite radius,

the signal attenuation obeys (10.19), being the equivalent of the EISF of

QENS. By assuming that the crystallites may be approximated by spheres

with mean square radius R

, (10.19) approaches [6–9]

∞

(γδg)=exp



−



(10.20)

corresponding to an eﬀective diﬀusivity

eﬀ

5∆

. (10.21)

The root mean square radius obtained via (10.21) with the experimental

value of D

eﬀ

(2 ·10

−10

−1

) does in fact coincide with the microscopically

determined mean crystallite radius of 2 µm. Finally, for temperatures above

290 K, the thermal energy of the molecules is high enough so that a suﬃciently

large number of molecules is able to leave the individual crystallites during

the observation time. Molecular transport is now determined by long-range

diﬀusion (situation in Fig. 10.1 (b) at 223 K and 293 K).

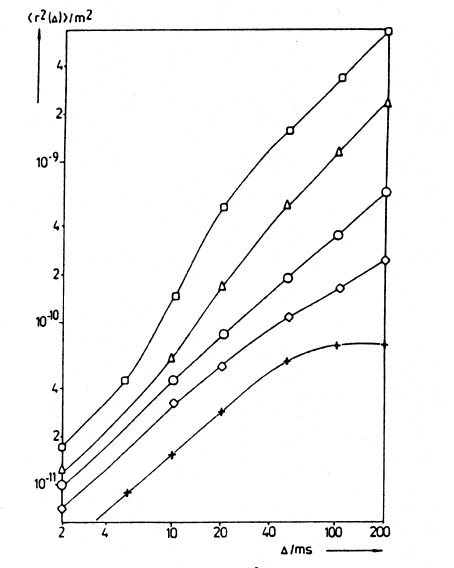
Deviations from normal diﬀusion become immediately visible by repre-

senting the mean square displacement as a function of the observation time.

As an example, Fig. 10.4 shows the mean square displacement of n-butane

in a bed of zeolite crystallites of type NaX with a mean diameter of 16 µm.

As expected, for displacements either much smaller or much larger than the

crystallite diameter, the mean square displacement is found to increase in

proportion with the observation time. This corresponds to the limiting cases

of intracrystalline and long-range diﬀusion. The trend of the deviations from

straight lines for displacements in the vicinity of the crystallite diameters may

be easily rationalized on the basis of (10.1). In contrast to normal diﬀusion,

the cross terms are not negligible anymore. At low temperatures, molecules

encountering the crystallite surface are more likely reversed in the direction of

propagation. This leads to negative cross terms and hence to deviations of the

mean square displacement to lower values. At high temperatures, molecules

encountering the surface may easily escape into the intercrystalline space and

proﬁt by the high intercrystalline mobility. Subsequent steps are therefore

more likely to be oriented into the same direction, leading to an enhance-

ment in the mean square displacements in comparison with linearity in time.

430 J¨org K¨arger and Frank Stallmach

Fig. 10.4. Mean square displacements r

(∆) of n-butane on zeolite NaX with

a mean crystallite diameter of 16 µm at a sorbate concentration of 80 mg/gat

183 K(+), 223 K(3), 243 K (

), 258 K(), and 273 K(2), respectively, in depen-

dence on the observation time ∆ [39].

10.4.2 Intracrystalline Self-Diﬀusion

The MD simulations presented in this textbook (Chap. 23, Sect. 23.4) are

exclusively devoted to the regime of intracrystalline zeolitic diﬀusion. A sur-

vey of the diﬀerent patterns of concentration dependence so far obtained

experimentally is displayed in Fig. 10.5. Depending on the nature of the sys-

tem under study, the self-diﬀusivity may vary with varying concentration in

quite diﬀerent ways. A decrease of molecular mobility with increasing con-

centration (patterns 1 and 2) may intuitively be understood by the increasing

mutual hindrance of the molecules, while any other dependence indicates the

dominating inﬂuence of the interaction between the diﬀusants and the zeolite

pore network. This tendency is demonstrated quantitatively in Sect. 23.4 of

Chap. 23 (Fig. 23.11, right), where the diﬀusivity is found to decrease with

increasing loading for large diameters of the “windows” between adjacent

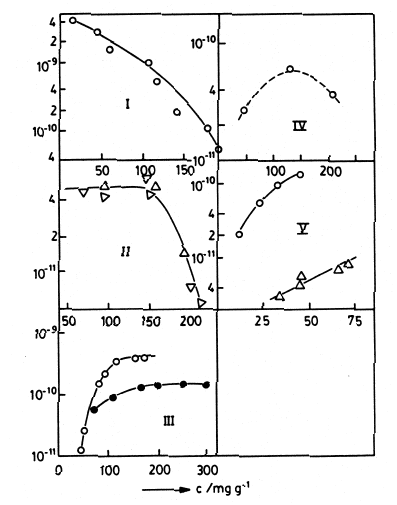
10 PFG NMR Studies of Anomalous Diﬀusion 431

D/m s

2-1

Fig. 10.5. Patterns of concentration dependence of intracrystalline self-diﬀusivities

as determined from PFG NMR measurements. (I) n-hexane in NaX at 358 K; (II)

ortho (), meta () and para () xylenes in NaX at 293 K; (III) ammonia (

)

and water (•) in NaX at 298 K; (IV) acetonitrile in NaX at 393 K; (V) ethane (

)

at 173 K and propane () at 413 K in NaCaA [3].

pores (dominating interaction between the diﬀusants) while it increases for

small windows (dominating inﬂuence of the pore system) [12].

10.4.3 Correlated Diﬀusion Anisotropy

The fact that zeolitic diﬀusion has to proceed in a well-deﬁned network of

pores and channels gives rise to a special type of correlation in the path of

molecular propagation. While the correlation eﬀect in solids (see Sects. 1.6.1

in Chap. 1 and 18.4.3 in Chap. 18) refers to the orientation of subsequent

steps, correlation in zeolitic diﬀusion eﬀects that propagation in diﬀerent

directions may not be independent from each other. As an example, Fig. 10.6

schematically represents the channel network of zeolite ZSM-5 by showing the

axes of the so-called straight channels (in y-direction) and of the sinusoidal

ones (in x-direction). Obviously, molecular propagation in z-direction implies

alternating displacements in x-andy-directions, so that the diﬀusivities in

these three directions (the principal elements of the diﬀusion tensor – see

(1.2) of Chap. 1) are correlated with each other. Under the assumption that

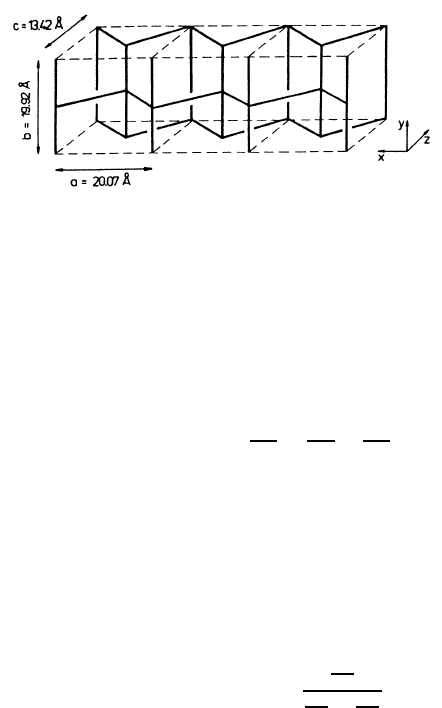
432 J¨org K¨arger and Frank Stallmach

Fig. 10.6. Outline of the channel network of ZSM-5 type zeolites over three ad-

jacent unit cells. The straight and zig-zag channels are oriented along the y and x

directions, respectively.

molecular displacements between the intersections of the channel network

are independent from each other, the correlation rule of zeolitic diﬀusion in

ZSM-5 may be shown to read [40]

, (10.22)

where a, b and c denote the dimensions of the unit cell as indicated in

Fig. 10.6. It has been conﬁrmed by MD simulations [41] that (10.22) provides

an excellent ﬁrst-order estimate of diﬀusion anisotropy in zeolites ZSM-5 and

silicalite-1, and may thus serve as a reasonable starting point for PFG NMR

measurements of diﬀusion anisotropy in ZSM-5 by PFG NMR [42].

Deviations from (10.22) have been quantitatively accounted for in [43] by

introducing a memory parameter β via the equation

β =

(10.23)

Comparison with (10.22) yields β = 1 for the no-memory case. Since

molecular propagation in z-direction can only occur in consequence of particle

exchange between diﬀerent types of channel segments, β>1 (i.e. a diminished

value of D

) indicates that molecular propagation tends to proceed within one

and the same type of channel, while β<1 refers to enhanced exchange rates.

These diﬀerences may be easily taken account of by allowing for a particle

memory, which permits the particles to choose their further migration path

depending on the channel segment along which they have got to a given

channel intersection [44,45] .

10.4.4 Transport Diﬀusion Versus Self-Diﬀusion

From a practical point of view, molecular transport under the inﬂuence of

concentration gradients is of much greater relevance than self-diﬀusion, since

10 PFG NMR Studies of Anomalous Diﬀusion 433

transport diﬀusion may be the rate limiting step for a number of applications.

The coeﬃcients of transport diﬀusion (D

, in the terminology of QENS – see

Sect. 3.11 in Chap. 3 – generally referred to as the coeﬃcient of chemical

or collective diﬀusion) is usually related to the self-diﬀusivity by the Darken

relation (see Chap. 14, Sect. 14.3 and [3], p. 13)

= D

dµ

= D

dlnp

dlnc

, (10.24)

where µ is the chemical potential of the diﬀusing species and p denotes the

equilibrium pressure necessary to maintain the sorbate at concentration c.

The “thermodynamic factor” d ln p/dlnc may be easily determined from the

adsorption isotherm c(p). The notation of (10.24) is correct under the as-

sumption of an ideal gas phase. Otherwise, the thermodynamic factor has to

be used in the more rigorous form

dµ/dlnc. This is the notation used,

e.g., in Sect. 3.12 of Chap. 3. Equation (10.24) implies in particular the quite

general result that in the limit of small concentrations (i.e. for c ∝ p)theco-

eﬃcients of transport diﬀusion and self-diﬀusion coincide. Exactly the same

message is provided by diﬀusion studies with liquid mixtures, where at trace

concentration of a component the self-diﬀusion coeﬃcient of this component

approaches the mutual diﬀusion coeﬃcient (Chap. 14, Sect. 14.3).

In contrast to these theoretical predictions, the comparison between the

transport diﬀusivities deduced from uptake experiments and the PFG NMR

self-diﬀusivity data yielded remarkable discrepancies [38, 46]. A critical re-

consideration of the uptake experiments has revealed that in many cases

molecular uptake was controlled by processes diﬀerent from intracrystalline

diﬀusion. The message of PFG NMR about diﬀusion in zeolites has thus

revolutionized the up to this time generally accepted picture, leading to sub-

stantially larger diﬀusivities [3]. However, even now the data on transport

diﬀusion and self-diﬀusion are not entirely compatible. It is interesting to

note that systems showing satisfactory agreement follow the concentration

patterns (iii) to (v) of self-diﬀusion (see Fig. 10.5) while in the case of con-

centration patterns (i) and (ii) the self-diﬀusivities are often found to be up

to two orders of magnitude larger than expected on the basis of the trans-

port diﬀusivities resulting from uptake experiments. In complete agreement

with this ﬁnding, MD simulations with methane in zeolite NaCaA (pattern

(v)) reveal satisfactory agreement between the transport and self-diﬀusivities

(see Fig. 23.20 right, of Chap. 23). As a possible explanation of this ﬁnding

one should have in mind that (10.24) is not strictly correct. On the basis of

the linear response theory (see Sects. 14.5 and 14.6 in Chap. 14 and 23.2.2 in

Chap. 23) the self-diﬀusivity (cf. (14.28) in Chap. 14 and (23.15) in Chap. 23)

is found to be

D =



∞



v

(0)v

(t)dt (10.25)

and the transport diﬀusivity (cf. (14.32) in Chap. 14)

434 J¨org K¨arger and Frank Stallmach



i,j

∞



v

(0)v

(t)dt · dlnp/dlnc (10.26)

with N and v

(t) denoting the number of diﬀusants and the velocity of the

i-th diﬀusant at time t, respectively. Obviously, the Darken relation (10.24)

is an immediate consequence of (10.25) and (10.26) for negligible cross terms

v

(0)v

(t) between the velocities of diﬀerent particles. One may speculate

that such a situation can in particular occur for dominating interaction be-

tween the diﬀusants and the zeolite lattice. From this point of view, the

agreement of transport and self-diﬀusivity data with (10.24) for systems fol-

lowing the concentration patterns (iii) to (v) is not unexpected. Similarly,

the mutual interaction between the diﬀusants for concentration patterns (i)

and (ii) should lead to deviations from (10.24). Since, however, the largest

discrepancies are observed for the smallest concentrations, where the mutual

interaction must be expected to vanish, the proposed explanation is still far

from exhaustive [47].

10.4.5 Single-File Diﬀusion

Molecular motion in one-dimensional channels is subject to a special pat-

tern of propagation if mutual passages of the molecules are excluded. This

is the famous case of single-ﬁle diﬀusion considered in detail in Chap. 18,

Sect. 18.4.4. As a consequence of the conﬁnement by the other diﬀusants,

the propagation of an arbitrarily selected molecule, albeit proceeding in a

completely regular pore network, is subjected to anomalous diﬀusion. Any

displacement in a certain direction is only possible if the molecules in front of

the diﬀusant under study are shifted into the same direction. This would lead

to an enhanced particle concentration just in front and to a smaller concentra-

tion behind the diﬀusant under consideration. Subsequent displacements are

therefore more likely to proceed into the opposite direction, tending to equi-

librate concentration. In contrast to diﬀusion in solids (Chap. 1, Sect. 1.6.1

and Chap. 18, Sect. 18.4.3), the signiﬁcance of this correlation increases with

increasing displacements. The larger the displacements in one direction are,

the larger is the probability that they are followed by displacements in the

opposite direction. As a consequence, the cross term in (10.1) becomes in-

creasingly important, leading to an exponent κ smaller than one in the time

law for the mean square displacement. As the rigorous result ((18.107) of

Chap. 18) one obtains

z

(t) =2F

√

t (10.27)

with

F = λ

1 − θ

√

2πτ

, (10.28)

where in analogy to the Einstein relation (cf. (10.8)) the mobility factor F

has been introduced [48]. Equations (10.27) and (10.28) are derived under