Хант Р.В.Г. Цветовоспроизведение

Подождите немного. Документ загружается.

ПРИЛОЖЕНИЯ

П1 КОЛОРИМЕТРИЧЕСКИЕ

МАТРИЦЫ

П1.1 ОБЩИЕ ПРИНЦИПЫ

атричная алгебра весьма подходит к разного рода колориметрическим расче

там, выполняемым, например, при маскировании, сканировании, теоретиче

ских построениях и пр. В данном Приложении мы сделаем краткий экскурс к основам

матричной алгебры и дадим ряд примеров ее применения в базовой колориметрии (ко

лориметрии цветовых воздействий. — Прим. пер.).

Итак, матрица — это массив цифр или символов. К примеру, обе записи:

271 18

671 12

или

xxx

123

456

789

являются матрицами.

Если две матрицы равны друг другу, каждый показатель первой матрицы равен со

ответствующему показателю второй матрицы, например, уравнение:

xxb

ycy

61 3

12 6

представляет собой вариант записи четырех уравнений:

xxbde

yc y f

61 3

12 6

=+=+

+= =

Когда система уравнений записывается в матричной форме, то систему эту можно

упростить путем разложения на множители, к примеру, система из двух уравнений:

ax a y a

ax ay a

12 5

34 6

в матричной форме записывается как:

ax a y

ax ay

а после разложения на множители:

853

Таким образом, в матричной алгебре действует т.н. правило умножения, и в данном

случае элементы первого ряда первой матрицы последовательно умножаются на эле

менты колонки второй матрицы, а результат суммируется, давая элементы первого

ряда матричного произведения. Элементы второго ряда матричного произведения по

лучаются аналогичным образом из элементов второго ряда первой матрицы.

Итак, в общем виде правило умножения звучит так:

Элемент, находящийся в mряду и nколонке матричного произведения, являет

ся суммой последовательных умножений элементов mряда первой матрицы на

элементы nколонки второй матрицы.

Таким образом:

ab ab ab ab

11 2 2 13 2

31 42 33 44

ab ab ab ab++

В матричной форме математические преобразования выглядят компактно и про

сто. Если, к примеру:

ax a y a

ax ay a

bx b y x

bx by y

12 5

34 6

то в матричном представлении эта система будет записана так:

и следовательно:

Правомочность такой замены легко проверить перемножением матриц и сравнени

ем с двумя уравнениями, полученными обычным способом. Стоит отметить, однако,

что последовательность матриц критична и не должна меняться, к примеру: если две

исходных матрицы обозначить как А и В, то

AB BA×¹×

Матричная алгебра очень удобна в решении систем уравнений, часто встречаю

щихся при колориметрических вычислениях. С целью упрощения вычислений ис

пользуются две вторичных матрицы:

транспозиция Аматрицы, получаемая записью рядов как колонок и колонок

как рядов;

adj. А =

дополнительная (сопряженная)кАматрице, получаемая путем замены ка

ждого элемента исходной матрицы на определитель этой же матрицы, но с вычеркну



тыми рядом и колонкой данного элемента и с последующим транспонированием ре



854

ПРИЛОЖЕНИЕ 1 КОЛОРИМЕТРИЧЕСКИЕ МАТРИЦЫ

зультата такой замены; нечетные элементы вписываются в новую матрицу со знаком

«минус», к примеру, если:

aaa

123

456

789

то

aaa

147

258

369

adj. A

AA A

AAA

14 7

258

369

где

Aaaaa

15968

24967

ит.д.

Обратная, или реципрокальная, матрица A

–1

— это матрица, которая выражает ре

шение системы уравнений, например:

если

, то

С помощью простой алгебры легко показать, что обратная матрица рассчитывается

как:

adj.

где

— это определитель, соответствующий Аматрице. Следовательно, если:

aaa

123

456

789

aaa

123

456

789

то

A a aa aa a aa aa a aa aa=---+-

159 68 249 67 348 57

()()()

П1.2 ПРИМЕНЕНИЕ МАТРИЦ В КОЛОРИМЕТРИИ

Типичной колориметрической задачей является следующая: в некоем треугольни

ке цветностей, скажем XYZ, даны позиции трех кардинальных (воспроизводящих)

стимулов (R, G и B) некоей трихроматической цветовоспроизводящей системы. Требу

ется найти уравнения преобразования, позволяющие перенести в этот треугольник ре



855

ПРИЛОЖЕНИЕ 1 КОЛОРИМЕТРИЧЕСКИЕ МАТРИЦЫ

зультаты, полученные с использованием этой системы, при условии, что равновели



кие колориметрические количества кардинальных RGBстимулов воспроизводят не

кий белый стимул W. Следовательно, в общем виде ситуация будет выглядеть так:

() () () ()

() ( ) () ()

() (

RXYZ

GXYZ

µ++

aaa

123

456

)()()

() () () ()

() () ()

µ++

hhh

123

WXYZ

WXYj

()Z

где сумма коэффициентов в каждом из уравнений равна единице (к примеру:

aaa

123

1++=

Весьма удобно ввести постоянные k

, k

и k

, так как сие позволяет уйти от знака

пропорциональности, заменив его знаком эквивалентности:

kaaa

1123

2456

() () () ()

() ( ) () ()

(

RXYZ

GXYZ

º++

)()()()º++aaa

789

XYZ

а также постоянную k

, позволяющую переписать уравнения по W:

kHHH

kJJJ

4123

() () () ()

WXYZ

º++

где H

, H

и H

пропорциональны соответственно h

, h

и h

, но представляют фактиче

ские количества кардинальных RGBстимулов, необходимые уравниванию (т.е. вос

произведению) белого стимула W, и где J

, J

и J

пропорциональны соответственно j

и j

— это коэффициент фотометрической яркости стимула W).

Теперь нам нужно определить величины k

, k

и k

. Чтобы выполнить сие, необхо

димо решить приведенные выше уравнения по (X), (Y) и (Z).

Самый удобный способ решения — матричный. При этом потребуется найти матри

цу, обратную

aaa

123

456

789

Если последнюю обозначить как А, то:

aa aa aa aa aa aa

aa aa a

--- -

59 68 49 67 48 57

29 38 1

()

()aaa aaaa

aa aa aa aa aa aa

937 1827

26 35 16 34 15 24

---

--- -

()

123

456

789

bbb

258

369

bbb

Когда

aaa aaa aaa

123 456 7 89

1++=++=++=

(типичный случай), то:

856

ПРИЛОЖЕНИЕ 1 КОЛОРИМЕТРИЧЕСКИЕ МАТРИЦЫ

Abbb bbb bbb=++=++ =++

147 25 8 369

Поскольку решение последнего выражения предельно просто, то сие позволяет

проверить каждый элемент матрицы.

Разделив каждый элемент матрицы на

, получим:

ccc

123

456

789

В качестве финальной проверки выражение

ccc ccc ccc

123 456 7 89

1++=++=++=

должно быть истинным.

Теперь мы можем написать:

11 2 2 33

41 52

.()()()()

.( ) ( ) (

XRGB

º++

º+

ck ck ck

ck ck GB

ZRGB

)()

.()()()()

º++

ck ck ck

71 82 93

а заменяя (X), (Y) и (Z) в уравнении

kJJJ

4123

() () () ()WXYZ=++

и сравнивая результат с уравнением

kHHH

4123

() () () ()WRGB=++

мы получим:

k H Jc Jc Jc

kHJ

11112437

22122538

331

=++

()

(

cJcJc

32639

++)

Итак, коэффициенты k

, k

и k

вычислены и уравнения преобразования выглядят

следующим образом:

11 2 1 3 1

. ( ) ( )( ) ( )( ) ( )( )

.( ) ( )(

RXYZ

º++

ak ak ak

XYZ

RXY

)( )()( )()

. ( ) ( )( ) ( )( ) (

º++

ak ak

52 62

73 83

10 ak

)( )Z

Уравнения обратного преобразования запишутся так:

11 2 2 33

41 52

.()()()()

.( ) ( ) (

XRGB

º++

º+

ck ck ck

ck ck GB

ZRGB

)()

.()()()()

º++

ck ck ck

71 82 93

857

ПРИЛОЖЕНИЕ 1 КОЛОРИМЕТРИЧЕСКИЕ МАТРИЦЫ

Отметим, что обычно сумма коэффициентов в данных уравнениях не равна единице.

Довольно часто бывает удобным переписать приведенные выше уравнения в виде

зависимостей между трехстимульными значениями (см. раздел 8.4):

XakRakGakB

YakRakGakB

=++

()()()

()()( )

11 4 2 73

21 52 83

ZakRakGakB=++()()()

31 62 93

R ckX ckY ckZ

G ckX ckY ckZ

BckXck

=++

11 41 71

22 52 82

33 63

YckZ+

Вновь отметим, что обычно сумма коэффициентов в данных уравнениях не равна

единице.

Если

HHH

123

JJJ

123

, то в правой части приведенных выше уравнений

суммы коэффициентов по (R), (G) и (B) всегда равны H/J. То же относится к коэффи

циентам по X, Y и Z. Сумма коэффициентов по (X), (Y) и (Z) всегда равна J/H, и то же

относится к коэффициентам по R, G и B. Если J = H, то понятно, что сумма коэффици

ентов равна единице.

ПРИЛОЖЕНИЕ 1 КОЛОРИМЕТРИЧЕСКИЕ МАТРИЦЫ

П2 КОЛОРИМЕТРИЧЕСКИЕ

ТАБЛИЦЫ

П2.1 ВЫЧИСЛЕНИЕ КОЛОРИМЕТРИЧЕСКИХ ВЕЛИЧИН

данном приложении рассматривается методика расчета колориметрических

показателей

из спектрофотометрических данных.

Спектрофотометрические

данные можно представить в двух вариантах: либо в виде количеств света (фотометри

ческие единицы) по каждой из длин волн видимого спектра, либо в виде количеств

энергии (радиометрические единицы) по каждой из длин волн.

П2.1.1 Колориметрическое вычисление

из фотометрических величин

В данном случае расчеты выполняются с применением закона центра тяжести сме

си стимулов (см. разделы 7.6, 8.5 и 8.6). Если количества света по длинам волн l

, l

и т.д. равны L

, L

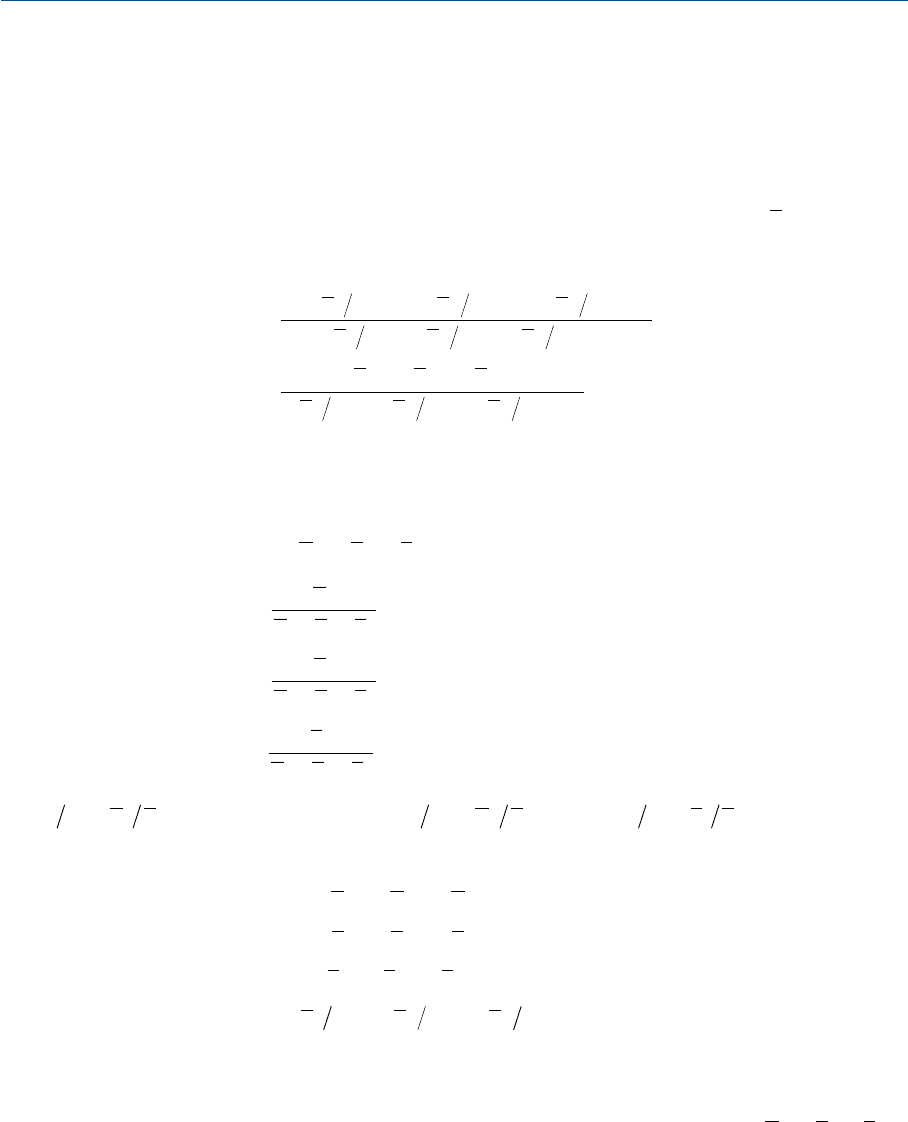
и т.д., то цветность результирующей смеси определяется вычис

лением центра тяжести весов:

на

и т.д.

где x

, x

и т.д. — координаты цветности (в системе XYZ) монохроматических

стимулов с длинами волн соответственно l

, l

и т.д. Координаты цветности центра

тяжести (x

) такой системы рассчитываются по уравнениям:

xL y xL y xL y

Ly Ly Ly

+++

11 1 22 2 33 3

11 22 3 3

...

Ly yLy yLy

Ly Ly Ly

LLL

11 222 333

11 22 3 3

123

+++

...

Ly Ly Ly

11 22 3 3

+++

в которые можно подставить значения из таблиц раздела П2.2: величины x и y в этих

таблицах даны по монохроматам диапазона от 380 до 780 нм (шаг 10 нм).

859

Т.е. показателей цветовых воздействий стимулов на зрительную систему наблюдателя. —

Прим. пер.

Т.е. физических характеристик стимулов. — Прим. пер.

П2.1.2 Колориметрическое вычисление

из радиометрических величин

В данном случае вычисления выполняются из величин мощности (энергии) стиму

ла по каждой из длин волн — e(l). Понятно, что величины эти вначале следует конвер

тировать в величины фотометрические умножением каждого значения e(l) на соответ

ствующее значение функции спектральной фотопической световой эффективности

V(l) — см. раздел 8.5. Ординаты функции V(l) принято обозначаь как

y()l

, поэтому

уравнения расчета выглядят следующим образом:

xeyy xeyy xeyy

ey y ey y ey

+++

11 1 1 22 2 2 33 3 3

11 1 22 2 3

...

11 22 33

11 1 22 2 33 3

ey ey ey

ey y ey y ey y

+++

...

Однако поскольку координаты цветностей x, y, z монохроматических

(т.е. спектральночистых) стимулов, которые, напомним, являются слагаемыми сти

мула исследуемого (закон аддитивности) соотносятся с трихроматическими кривыми

Стандартного наблюдателя

x()l

y()l

z()l

по выражениям:

xyz

111

то

xy xy

11 11

и т.д., и аналогично

xy xy

22 22

и т.д.,

zy zy

11 11

и т.д. Следова

тельно, суммирование упрощается до:

S x ex ex ex X

S y ey ey ey

mm m

=+++=

11 22 33

...

S z ez ez ez Z

Seyyeyyeyy

mm m

=+++=

=++

11 2 2 3 3

11 1 2 2 2 33

...

Итак, мы видим, что предпочтительнее, когда физические параметры стимула

представлены в радиометрических единицах (нежели в фотометрических) поскольку

тогда появляется возможность использовать табулированные величины

x()l

y()l

z()l

то есть прописанные в уже упомянутых таблицах раздела П2.2 (2° Стандартный на

блюдатель, диапазон от 380 до 780 нм, шаг — 10 нм).

Когда X

, Y

, Z

и S

вычислены, можно рассчитать величины x

, y

, z

. Проверить

же вычисление можно просуммировав полученные данные: в сумме должна получить

ся единица (разумеется, можно выполнить и индивидуальные проверки просумми

ровав X, Y и Z каждого монохромата:

XYZ S

111 1

++=

и т.д.).

860

ПРИЛОЖЕНИЕ 2 КОЛОРИМЕТРИЧЕСКИЕ ТАБЛИЦЫ