Hahn Th. (ed.) International tables for crystallography. Vol. A. Space-group symmetry
Подождите немного. Документ загружается.

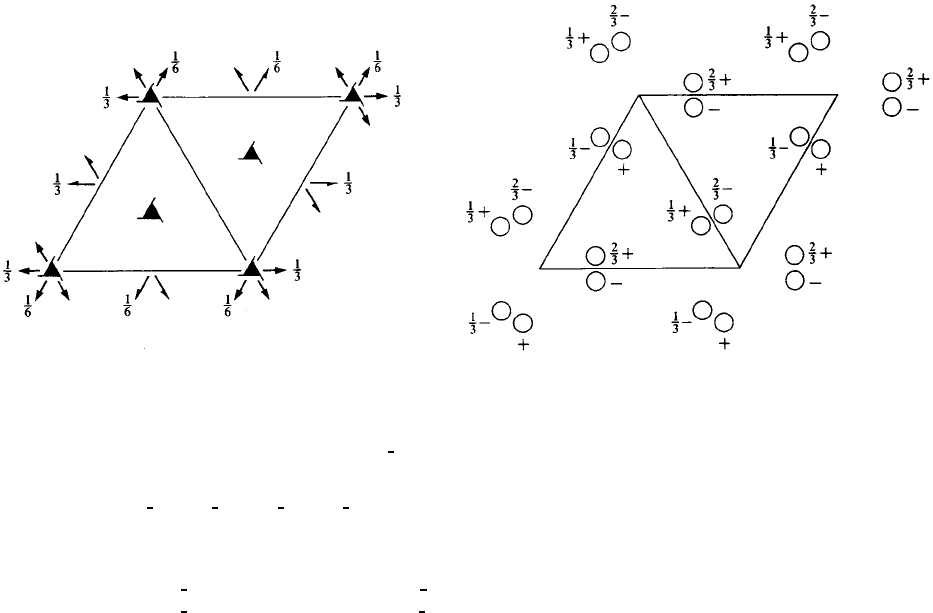
P3
2
21 D
6
3
321 Trigonal
No. 154 P3
2
21 Patterson symmetry P
¯
3m1
Origin on 2[110] at 3
2
(1,1, 2)1
Asymmetric unit 0 ≤ x ≤ 1; 0 ≤ y ≤ 1; 0 ≤ z ≤
1
6
Vertices 0,0, 01,0, 01,1,00,1, 0
0,0,
1
6
1,0,
1
6
1,1,
1
6
0,1,
1
6
Symmetry operations
(1) 1 (2) 3
+
(0,0,
2
3
) 0,0,z (3) 3
−
(0,0,
1
3
) 0,0,z
(4) 2 x,x,0(5)2x,0,
1
6
(6) 2 0, y,
1
3
514
International Tables for Crystallography (2006). Vol. A, Space group 154, pp. 514–515.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 154 P3
2
21
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (4)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
6 c 1(1)x,y,z (2) ¯y,x − y,z +
2
3
(3) ¯x+ y, ¯x,z +
1
3
(4) y,x, ¯z (5) x − y, ¯y, ¯z +
1
3
(6) ¯x, ¯x + y, ¯z+
2
3
000l : l = 3n
Special: no extra conditions
3 b . 2 . x,0,
1
6
0,x,
5
6
¯x, ¯x,
1
2
3 a . 2 . x,0,
2
3
0,x,
1
3
¯x, ¯x, 0
Symmetry of special projections
Along [001] p31m
a
= ab
= b
Origin at 0,0,z
Along [100] p2
a
=
1
2
(a + 2b) b
= c
Origin at x,0,
1
6
Along [210] p11m
a
=
1
2
bb
= c
Origin at x,
1
2
x,
1
3
Maximal non-isomorphic subgroups
I
[2] P3
2
11(P3
2
, 145) 1; 2; 3
[3] P121 (C2, 5) 1; 4
[3] P121 (C2, 5) 1; 5
[3] P121 (C2, 5) 1; 6
IIa none
IIb [3] H 3
2
21(a
= 3a,b
= 3b)(P3
2
12, 153)
Maximal isomorphic subgroups of lowest index
IIc
[2] P3
1
21(c
= 2c) (152); [4] P3
2
21(a
= 2a,b
= 2b) (154); [7] P3
2
21(c
= 7c) (154)
Minimal non-isomorphic supergroups
I
[2] P6
5
22 (179); [2] P6
2
22 (180)
II [3] H 3
2
21(P3
2
12, 153); [3] R32 (obverse) (155); [3] R32 (reverse) (155); [3] P321(c
=
1
3
c) (150)
515
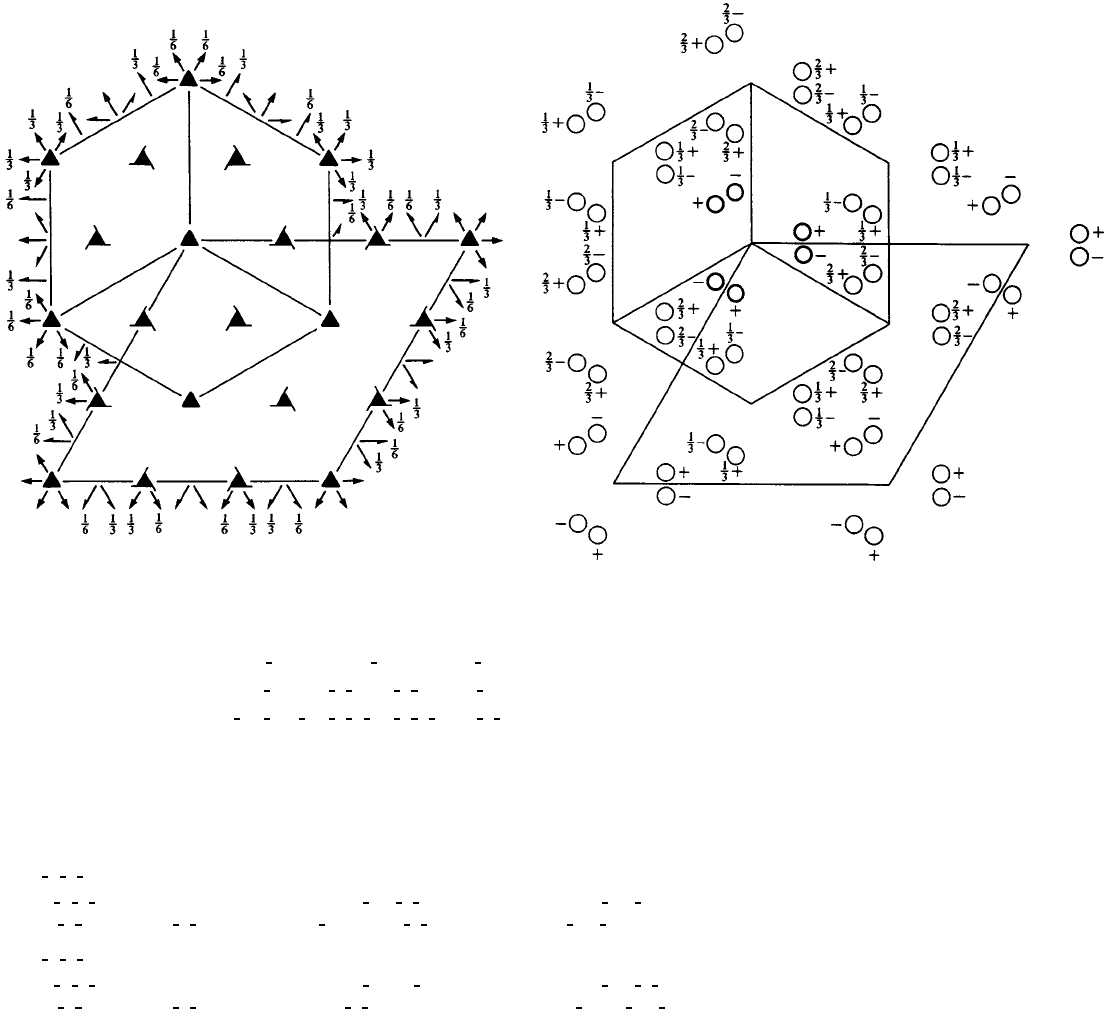
R32 D
7
3
32 Trigonal
No. 155 R32
Patterson symmetry R
¯
3m
HEXAGONAL AXES
Origin at 32
Asymmetric unit 0 ≤ x ≤
2
3
;0≤ y ≤
2
3
;0≤ z ≤
1
6
; x ≤ (1 + y)/2; y ≤ min(1 − x,(1 + x)/2)
Vertices 0,0, 0
1
2
,0, 0
2
3
,
1
3
,0
1
3
,
2
3
,00,
1
2
,0
0,0,
1
6
1
2
,0,
1
6
2
3
,
1
3
,
1
6
1
3
,
2
3
,
1
6
0,
1
2
,
1
6
Symmetry operations
For (0,0,0)+ set
(1) 1 (2) 3
+
0,0,z (3) 3
−
0,0,z
(4) 2 x,x,0(5)2x, 0,0(6)20,y,0
For (
2
3
,
1
3
,
1
3
)+ set
(1) t(
2
3
,
1
3
,
1
3
) (2) 3
+
(0,0,
1
3
)
1
3
,
1
3
,z (3) 3
−
(0,0,
1
3
)
1
3
,0, z
(4) 2(
1
2
,
1
2
,0) x, x −
1
6
,
1
6
(5) 2(
1
2
,0, 0) x,
1
6
,
1
6
(6) 2
1
3
,y,
1
6
For (
1
3
,
2
3
,
2
3
)+ set
(1) t(
1
3
,
2
3
,
2
3
) (2) 3
+
(0,0,
2
3
) 0,
1
3
,z (3) 3
−
(0,0,
2
3
)
1
3
,
1
3
,z
(4) 2(
1
2
,
1
2
,0) x, x +
1
6
,
1
3
(5) 2 x,
1
3
,
1
3
(6) 2(0,
1
2
,0)
1
6
,y,
1
3
516
International Tables for Crystallography (2006). Vol. A, Space group 155, pp. 516–519.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 155 R32
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); t(
2
3
,
1
3
,
1
3
); (2); (4)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates
(0,0, 0)+ (
2
3
,
1
3
,
1
3
)+ (
1
3
,
2
3
,
2
3
)+
Reflection conditions
General:
18 f 1(1)x,y,z (2) ¯y,x − y,z (3) ¯x + y, ¯x,z
(4) y,x, ¯z (5) x − y, ¯y, ¯z (6) ¯x, ¯x + y, ¯z
hkil : −h + k + l = 3n
hki0:−h + k = 3n
hh
2hl : l = 3n
h
¯
h0l : h + l = 3n
000l : l = 3n
h
¯
h00 : h = 3n
Special: no extra conditions
9 e . 2 x , 0,
1
2
0,x,
1
2
¯x, ¯x,
1
2
9 d . 2 x,0,00,x,0¯x, ¯x, 0
6 c 3 . 0,0,z 0,0, ¯z
3 b 32 0,0,
1
2
3 a 32 0,0,0
Symmetry of special projections
Along [001] p3m1
a
=
1
3
(2a + b) b
=
1
3
(−a + b)
Origin at 0,0,z
Along [100] p2
a
=
1
2
(a + 2b) b
=
1
3
(−a − 2b + c)
Origin at x,0,0
Along [210] p11m
a
=
1
2
bb
=
1
3
c
Origin at x,
1
2
x,0
Maximal non-isomorphic subgroups
I
[2] R31 (R3, 146) (1; 2; 3)+
[3] R12 (C2, 5) (1; 4)+
[3] R12 (C2, 5) (1; 5)+
[3] R12 (C2, 5) (1; 6)+
IIa
[3] P3
2
21 (154) 1; 4; (2; 6)+(
1
3
,
2
3
,
2
3
); (3; 5)+(
2
3
,
1
3
,
1
3
)
[3] P3
2
21 (154) 1; 5; (2; 4)+(
1
3
,
2
3
,
2
3
); (3; 6)+(
2
3
,
1
3
,
1
3
)
[3] P3
2
21 (154) 1; 6; (2; 5)+(
1
3
,
2
3
,
2
3
); (3; 4)+(
2
3
,
1
3
,
1
3
)
[3] P3
1
21 (152) 1; 4; (2; 6)+(
2
3
,
1
3
,
1
3
); (3; 5)+(
1
3
,
2
3
,
2
3
)
[3] P3
1
21 (152) 1; 5; (2; 4)+(
2
3
,
1
3
,
1
3
); (3; 6)+(
1
3
,
2
3
,
2
3
)
[3] P3
1
21 (152) 1; 6; (2; 5)+(
2
3
,
1
3
,
1
3
); (3; 4)+(
1
3
,
2
3
,
2
3
)
[3] P321 (150) 1; 2; 3; 4; 5; 6
[3] P321 (150) 1; 2; 3; (4; 5; 6)+(
1
3
,
2
3
,
2
3
)
[3] P321 (150) 1; 2; 3; (4; 5; 6)+(
2
3
,
1
3
,
1
3
)
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[2] R32 (a
= −a,b
= −b,c
= 2c) (155); [4] R32 (a
= −2a, b
= −2b) (155)
Minimal non-isomorphic supergroups
I
[2] R
¯
3m (166); [2] R
¯
3c (167); [4] P432 (207); [4] P4
2
32 (208); [4] F 432 (209); [4] F 4
1
32 (210); [4] I 432 (211);
[4] P4
3
32 (212); [4] P4
1
32 (213); [4] I 4
1
32 (214)
II [3] P312(a
=
1
3
(2a + b),b
=
1
3
(−a + b),c
=
1
3
c) (149)
517
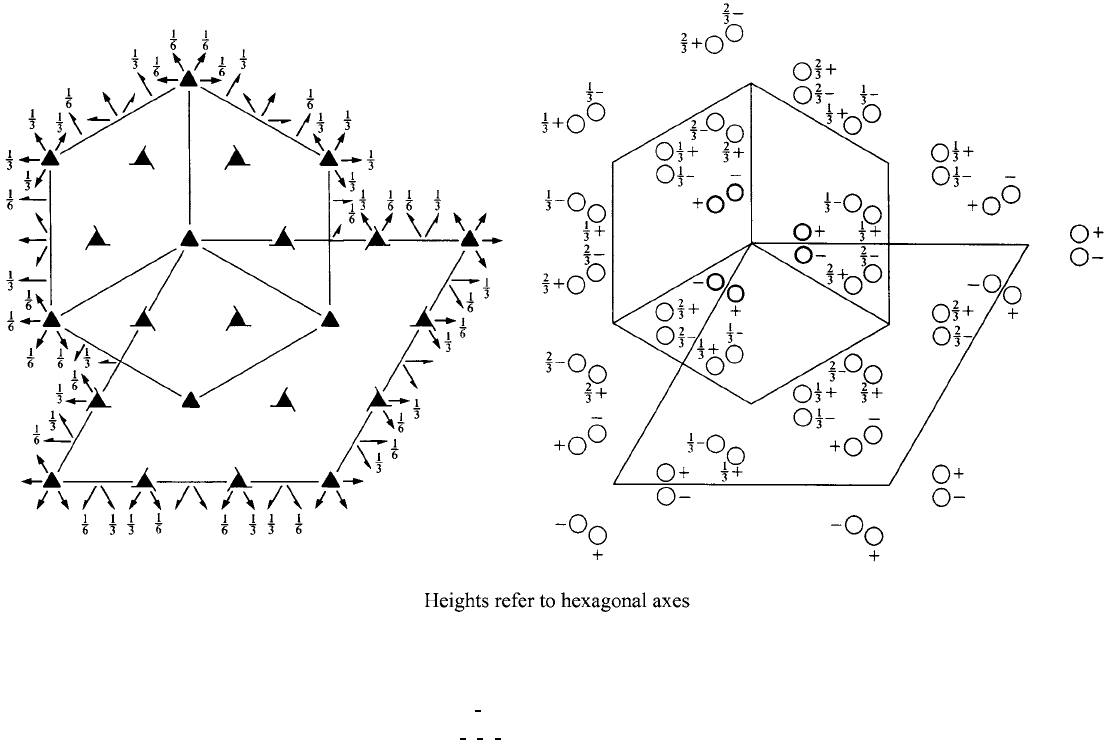
R32 D
7
3
32 Trigonal
No. 155 R32
Patterson symmetry R
¯
3m
RHOMBOHEDRAL AXES
Origin at 32
Asymmetric unit 0 ≤ x ≤ 1; 0 ≤ y ≤ 1; 0 ≤ z ≤
1
2
; z ≤ min(x,y,1 − x, 1 − y)
Vertices 0,0, 01,0, 01,1,00,1, 0
1
2
,
1
2
,
1
2
Symmetry operations
(1) 1 (2) 3
+
x,x, x (3) 3
−
x,x, x
(4) 2 ¯x,0,x (5) 2 x, ¯x,0(6)20,y, ¯y
518

CONTINUED No. 155 R32
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (4)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
6 f 1(1)x,y,z (2) z,x,y (3) y,z,x
(4) ¯z, ¯y, ¯x (5) ¯y, ¯x, ¯z (6) ¯x, ¯z, ¯y
no conditions
Special: no extra conditions
3 e . 2
1
2
,y, ¯y ¯y,
1
2
,yy, ¯y,
1
2
3 d . 20, y, ¯y ¯y,0,yy, ¯y,0
2 c 3 . x,x, x ¯x, ¯x, ¯x
1 b 32
1
2
,
1
2
,
1
2
1 a 32 0, 0,0
Symmetry of special projections
Along [111] p3m1
a
=
1
3
(2a − b− c) b
=
1
3
(−a + 2b − c)
Origin at x,x, x
Along [1
¯
10] p2
a
=
1
2
(a + b − 2c ) b
= c
Origin at x, ¯x,0
Along [2
¯
1
¯
1] p11m
a
=
1
2
(b− c) b
=
1
3
(a + b + c)
Origin at 2x, ¯x, ¯x
Maximal non-isomorphic subgroups
I
[2] R31 (R3, 146) 1; 2; 3
[3] R12 (C2, 5) 1; 4
[3] R12 (C2, 5) 1; 5
[3] R12 (C2, 5) 1; 6
IIa none
IIb [3] P321 (a
= a − b,b
= b − c,c
= a + b + c) (150); [3] P3
1
21(a
= a − b,b
= b − c,c
= a + b + c) (152);
[3] P3
2
21(a
= a − b,b
= b − c,c
= a + b + c) (154)
Maximal isomorphic subgroups of lowest index
IIc
[2] R32 (a
= b + c,b
= a + c,c
= a + b) (155); [4] R32(a
= −a + b + c,b
= a − b + c,c
= a + b − c) (155)
Minimal non-isomorphic supergroups
I
[2] R
¯
3m (166); [2] R
¯
3c (167); [4] P432 (207); [4] P4
2
32 (208); [4] F 432 (209); [4] F 4
1
32 (210); [4] I 432 (211);
[4] P4
3
32 (212); [4] P4
1
32 (213); [4] I 4
1
32 (214)
II [3] P312(a
=
1
3
(2a − b− c), b
=
1
3
(−a + 2b − c),c
=
1
3
(a + b + c)) (149)
519
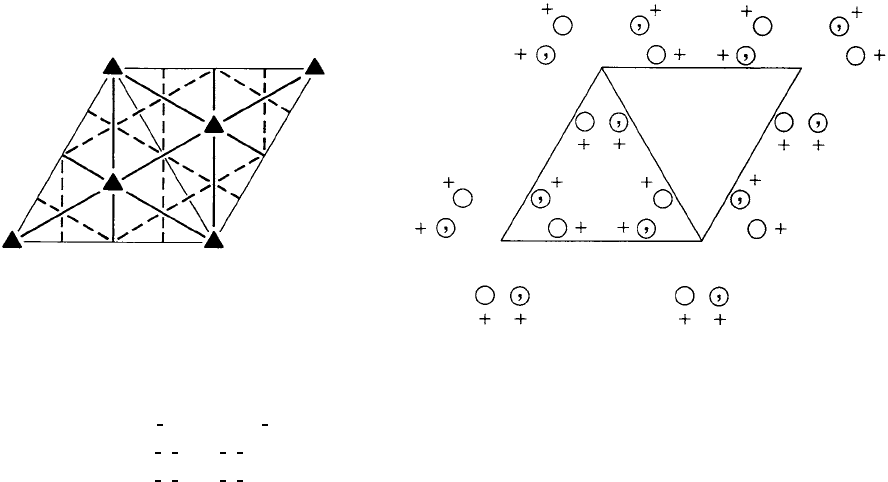
P3m1 C
1
3v
3m1 Trigonal
No. 156 P3m1
Patterson symmetry P
¯
3m1
Origin on 3m1
Asymmetric unit 0 ≤ x ≤
2
3
;0≤ y ≤
2
3
;0≤ z ≤ 1; x ≤ 2y; y ≤ min(1 − x,2x)
Vertices 0,0, 0
2
3
,
1
3
,0
1
3
,
2
3
,0
0,0,1
2
3
,
1
3
,1
1
3
,
2
3
,1
Symmetry operations
(1) 1 (2) 3
+
0,0,z (3) 3
−
0,0,z
(4) mx, ¯x, z (5) mx,2x,z (6) m 2x, x,z
520
International Tables for Crystallography (2006). Vol. A, Space group 156, pp. 520–521.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 156 P3m1
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (4)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
6 e 1(1)x,y,z (2) ¯y,x − y,z (3) ¯x + y, ¯x,z
(4) ¯y, ¯x,z (5) ¯x+ y,y, z (6) x,x − y,z
no conditions
Special: no extra conditions
3 d . m . x, ¯x,zx, 2x, z 2¯x, ¯x,z
1 c 3 m .
2
3
,
1
3
,z
1 b 3 m .
1
3
,
2
3
,z
1 a 3 m . 0,0,z
Symmetry of special projections
Along [001] p3m1
a
= ab
= b
Origin at 0,0,z
Along [100] p1
a
=
1
2
(a + 2b) b
= c
Origin at x,0,0
Along [210] p1m1
a
=
1
2
bb
= c
Origin at x,
1
2
x,0
Maximal non-isomorphic subgroups
I
[2] P311 (P3, 143) 1; 2; 3
[3] P1m1(Cm,8) 1; 4
[3] P1m1(Cm,8) 1; 5
[3] P1m1(Cm,8) 1; 6
IIa none
IIb [2] P3c1(c
= 2c) (158); [3] H 3m1(a
= 3a,b
= 3b)(P31m, 157)
Maximal isomorphic subgroups of lowest index
IIc
[2] P3m1(c
= 2c) (156); [4] P3m1(a
= 2a,b
= 2b) (156)
Minimal non-isomorphic supergroups
I
[2] P
¯
3m1 (164); [2] P6mm (183); [2] P6
3
mc(186); [2] P
¯
6m2 (187)
II [3] H 3m1(P31m, 157); [3] R3m (obverse) (160); [3] R3m (reverse) (160)
521
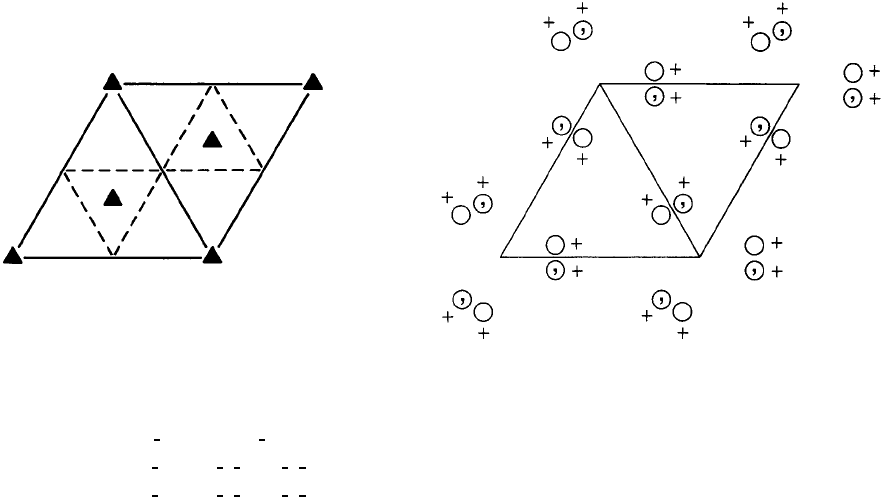
P31mC
2
3v
31m Trigonal
No. 157 P31m
Patterson symmetry P
¯
31m
Origin on 31m
Asymmetric unit 0 ≤ x ≤
2
3
;0≤ y ≤
1
2
;0≤ z ≤ 1; x ≤ (y + 1)/2; y ≤ min(1 − x,x)
Vertices 0,0, 0
1
2
,0, 0
2
3
,
1
3
,0
1
2
,
1
2
,0
0,0,1
1
2
,0, 1
2
3
,
1
3
,1
1
2
,
1
2
,1
Symmetry operations
(1) 1 (2) 3
+
0,0,z (3) 3
−
0,0,z
(4) mx,x,z (5) mx,0, z (6) m 0, y,z
522
International Tables for Crystallography (2006). Vol. A, Space group 157, pp. 522–523.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 157 P31m
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (4)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
6 d 1(1)x,y,z (2) ¯y,x − y,z (3) ¯x + y, ¯x,z
(4) y,x,z (5) x − y, ¯y,z (6) ¯x, ¯x+ y,z
no conditions
Special: no extra conditions
3 c ..mx, 0,z 0,x,z ¯x, ¯x,z
2 b 3 ..
1
3
,
2
3
,z
2
3
,
1
3
,z
1 a 3 . m 0,0,z
Symmetry of special projections
Along [001] p31m
a
= ab
= b
Origin at 0,0,z
Along [100] p1m1
a
=
1
2
(a + 2b) b
= c
Origin at x,0,0
Along [210] p1
a
=
1
2
bb
= c
Origin at x,
1
2
x,0
Maximal non-isomorphic subgroups
I
[2] P311 (P3, 143) 1; 2; 3
[3] P11m (Cm,8) 1; 4
[3] P11m (Cm,8) 1; 5
[3] P11m (Cm,8) 1; 6
IIa none
IIb [2] P31c (c
= 2c) (159); [3] H 31m (a
= 3a,b
= 3b)(P3m1, 156); [3] R3m (a
= a − b,b
= a + 2b,c
= 3c) (160);
[3] R3m (a
= 2a + b,b
= −a + b,c
= 3c) (160)
Maximal isomorphic subgroups of lowest index
IIc
[2] P31m (c
= 2c) (157); [4] P31m (a
= 2a,b
= 2b) (157)
Minimal non-isomorphic supergroups
I
[2] P
¯
31m (162); [2] P6mm (183); [2] P6
3
cm(185); [2] P
¯
62m (189)
II [3] H 31m (P3m1, 156)
523
