Hahn Th. (ed.) International tables for crystallography. Vol. A. Space-group symmetry
Подождите немного. Документ загружается.

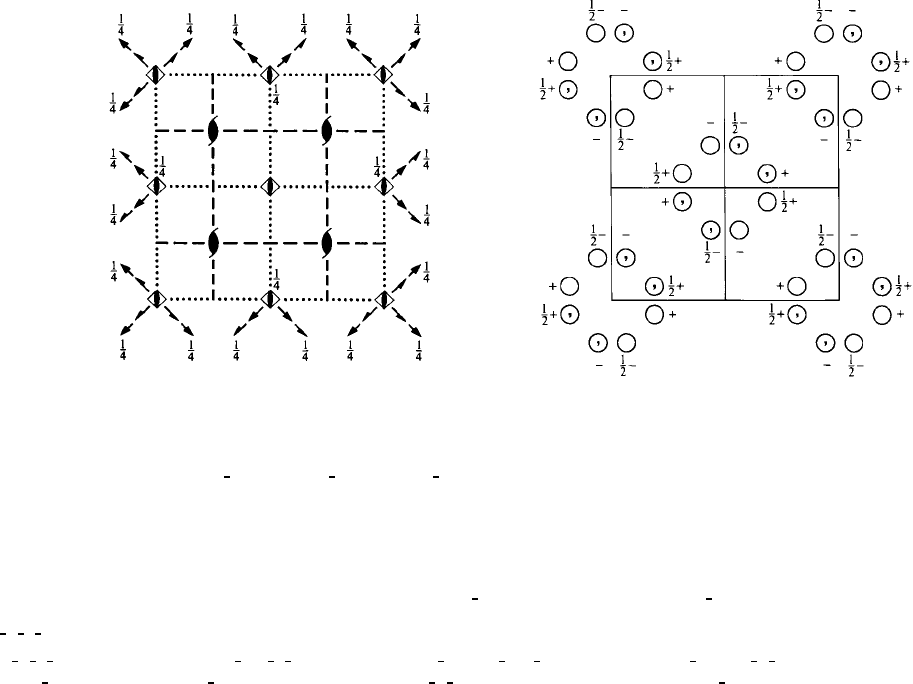
I
¯
4c2 D
10
2d
¯
4m2 Tetragonal
No. 120 I
¯
4c2
Patterson symmetry I 4/mmm
Origin at
¯
4c2
1
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
;0≤ z ≤
1
4
Symmetry operations
For (0,0,0)+ set
(1) 1 (2) 2 0,0, z (3)
¯
4
+
0,0,z;0,0, 0(4)
¯
4
−
0,0,z;0,0,0
(5) cx,0,z (6) c 0,y,z (7) 2 x,x,
1
4
(8) 2 x , ¯x,
1
4
For (
1
2
,
1
2
,
1
2
)+ set
(1) t(
1
2
,
1
2
,
1
2
) (2) 2(0,0,
1
2
)
1
4
,
1
4
,z (3)
¯
4
+
1
2
,0, z;
1
2
,0,
1
4
(4)
¯
4
−
0,
1
2
,z;0,
1
2
,
1
4
(5) ax,
1
4
,z (6) b
1
4
,y,z (7) 2(
1
2
,
1
2
,0) x, x,0(8)2x, ¯x +
1
2
,0
424
International Tables for Crystallography (2006). Vol. A, Space group 120, pp. 424–425.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 120 I
¯
4c2
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); t(
1
2
,
1
2
,
1
2
); (2); (3); (5)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates
(0,0, 0)+ (
1
2
,
1
2
,
1
2
)+
Reflection conditions
General:
16 i 1(1)x,y,z (2) ¯x, ¯y,z (3) y, ¯x, ¯z (4) ¯y,x, ¯z
(5) x, ¯y,z +
1
2
(6) ¯x,y, z +
1
2
(7) y,x, ¯z +
1
2
(8) ¯y, ¯x, ¯z +
1
2
hkl : h + k + l = 2n
hk0: h + k = 2n
0kl : k,l = 2n
hhl : l = 2n
00l : l = 2n
h00 : h = 2n
Special: as above, plus
8 h ..2 x,x +
1
2
,0¯x, ¯x+
1
2
,0 x +
1
2
, ¯x, 0¯x+
1
2
,x,0 no extra conditions
8 g 2 .. 0,
1
2
,z
1
2
,0, ¯z 0,
1
2
,z +
1
2
1
2
,0, ¯z +
1
2
hkl : l = 2n
8 f 2 .. 0,0,z 0,0, ¯z 0,0,z +
1
2
0,0, ¯z +
1
2
hkl : l = 2n
8 e ..2 x,x,
1
4
¯x, ¯x,
1
4
x, ¯x,
3
4
¯x,x,
3
4
no extra conditions
4 d 2 . 22 0,
1
2
,0
1
2
,0, 0 hkl : l = 2n
4 c
¯
4 .. 0 ,
1
2
,
1
4
0,
1
2
,
3
4
hkl : l = 2n
4 b
¯
4 .. 0 , 0,00, 0,
1
2
hkl : l = 2n
4 a 2 . 22 0,0,
1
4
0,0,
3
4
hkl : l = 2n
Symmetry of special projections
Along [001] p4mm
a
=
1
2
(a − b) b
=
1
2
(a + b)
Origin at 0,0,z
Along [100] p1m1
a
=
1
2
bb
=
1
2
c
Origin at x,0,0
Along [110] p2mm
a
=
1
2
(−a + b) b
=
1
2
c
Origin at x,x , 0
Maximal non-isomorphic subgroups
I
[2] I
¯
411(I
¯
4, 82) (1; 2; 3; 4)+
[2] I 2c1(Iba2, 45) (1; 2; 5; 6)+
[2] I 212(F 222, 22) (1; 2; 7; 8)+
IIa [2] P
¯
4b2 (117) 1; 2; 3; 4; (5; 6; 7; 8)+(
1
2
,
1
2
,
1
2
)
[2] P
¯
4b2 (117) 1; 2; 7; 8; (3; 4; 5; 6)+(
1
2
,
1
2
,
1
2
)
[2] P
¯
4c2 (116) 1; 2; 3; 4; 5; 6; 7; 8
[2] P
¯
4c2 (116) 1; 2; 5; 6; (3; 4; 7; 8)+(
1
2
,
1
2
,
1
2
)
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[3] I
¯
4c2(c
= 3c) (120); [9] I
¯
4c2(a
= 3a,b
= 3b) (120)
Minimal non-isomorphic supergroups
I
[2] I 4/mcm(140); [2] I 4
1
/acd (142); [3] F
¯
43c (219)
II [2] C
¯
4m2(c
=
1
2
c)(P
¯
42m, 111)
425
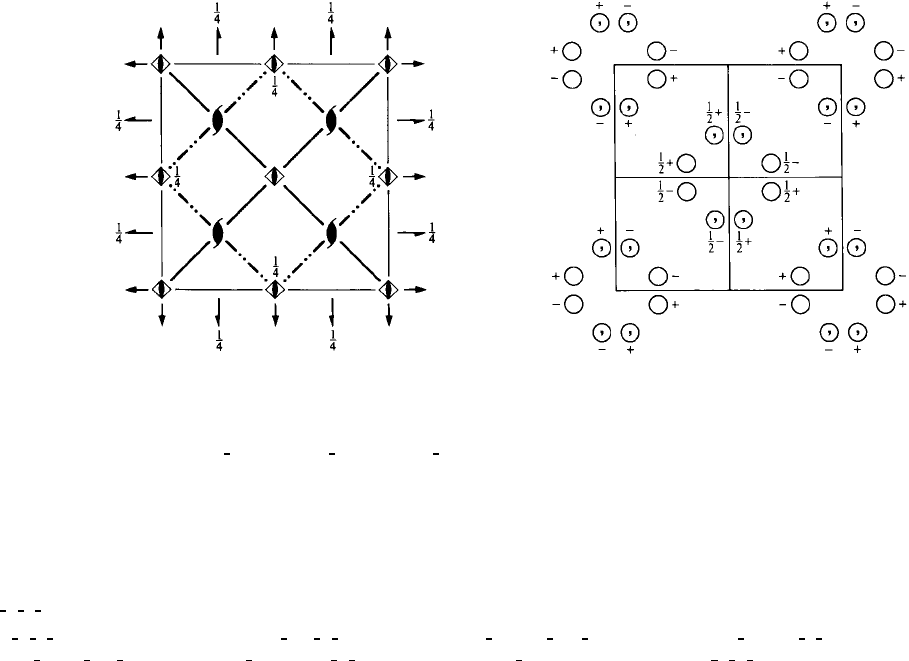
I
¯
42mD
11
2d
¯
42m Tetragonal
No. 121 I
¯
42m
Patterson symmetry I 4/mmm
Origin at
¯
42m
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
;0≤ z ≤
1
2
; x ≤ y
Symmetry operations
For (0,0,0)+ set
(1) 1 (2) 2 0,0,z (3)
¯
4
+
0,0,z;0,0,0(4)
¯
4
−
0,0,z;0,0, 0
(5) 2 0,y, 0(6)2x,0,0(7)mx, ¯x,z (8) mx,x,z
For (
1
2
,
1
2
,
1
2
)+ set
(1) t(
1
2
,
1
2
,
1
2
) (2) 2(0,0,
1
2
)
1
4
,
1
4
,z (3)
¯
4
+
1
2
,0, z;
1
2
,0,
1
4
(4)
¯
4
−
0,
1
2
,z;0,
1
2
,
1
4
(5) 2(0,
1
2
,0)
1
4
,y,
1
4
(6) 2(
1
2
,0, 0) x,
1
4
,
1
4
(7) cx+
1
2
, ¯x,z (8) n(
1
2
,
1
2
,
1
2
) x,x,z
426
International Tables for Crystallography (2006). Vol. A, Space group 121, pp. 426–427.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 121 I
¯
42m
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); t(
1
2
,
1
2
,
1
2
); (2); (3); (5)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates
(0,0, 0)+ (
1
2
,
1
2
,
1
2
)+
Reflection conditions
General:
16 j 1(1)x,y,z (2) ¯x, ¯y,z (3) y, ¯x, ¯z (4) ¯y,x, ¯z
(5) ¯x, y, ¯z (6) x, ¯y, ¯z (7) ¯y, ¯x,z (8) y,x,z
hkl : h + k + l = 2n
hk0: h + k = 2n
0kl : k + l = 2n
hhl : l = 2n
00l : l = 2
n
h00 : h = 2n
Special: as above, plus
8 i ..mx,x,z ¯x, ¯x,zx, ¯x, ¯z ¯x, x, ¯z no extra conditions
8 h 2 .. 0,
1
2
,z
1
2
,0, ¯z 0,
1
2
, ¯z
1
2
,0, zhkl: l = 2n
8 g . 2 . x,0,
1
2
¯x,0,
1
2
0, ¯x,
1
2
0,x,
1
2
no extra conditions
8 f . 2 . x,0, 0¯x,0, 00, ¯x, 00,x,0 no extra conditions
4 e 2 . mm 0, 0,z 0,0, ¯z no extra conditions
4 d
¯
4 .. 0,
1
2
,
1
4
0,
1
2
,
3
4
hkl : l = 2n
4 c 222. 0,
1
2
,0
1
2
,0, 0 hkl : l = 2n
2 b
¯
42m 0,0,
1
2
no extra conditions
2 a
¯
42m 0,0,0 no extra conditions
Symmetry of special projections
Along [001] p4mm
a
=
1
2
(a − b) b
=
1
2
(a + b)
Origin at 0,0,z
Along [100] c2mm
a
= bb
= c
Origin at x,0,0
Along [110] p1m1
a
=
1
2
(−a + b) b
=
1
2
c
Origin at x,x , 0
Maximal non-isomorphic subgroups
I
[2] I
¯
411(I
¯
4, 82) (1; 2; 3; 4)+
[2] I 21m (Fmm2, 42) (1; 2; 7; 8)+
[2] I 221(I 222, 23) (1; 2; 5; 6)+
IIa [2] P
¯
42
1
c (114) 1; 2; 3; 4; (5; 6; 7; 8)+(
1
2
,
1
2
,
1
2
)
[2] P
¯
42
1
m (113) 1; 2; 7; 8; (3; 4; 5; 6)+(
1
2
,
1
2
,
1
2
)
[2] P
¯
42c (112) 1; 2; 5; 6; (3; 4; 7; 8)+(
1
2
,
1
2
,
1
2
)
[2] P
¯
42m (111) 1; 2; 3; 4; 5; 6; 7; 8
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[3] I
¯
42m (c
= 3c) (121); [9] I
¯
42m (a
= 3a,b
= 3b) (121)
Minimal non-isomorphic supergroups
I
[2] I 4/mmm(139); [2] I 4/mcm(140); [3] I
¯
43m (217)
II [2] C
¯
42m (c
=
1
2
c)(P
¯
4m2, 115)
427
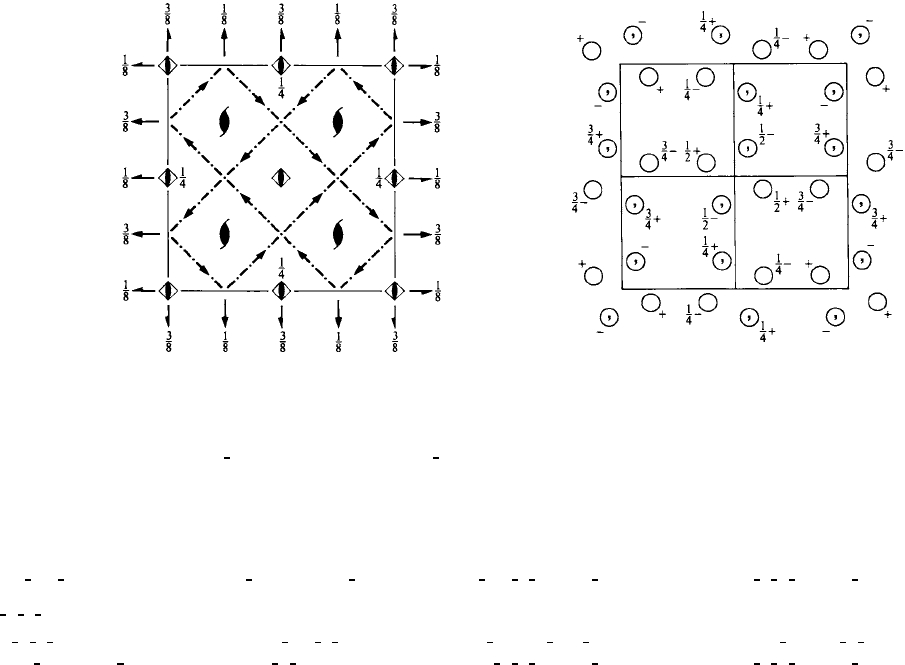
I
¯
42dD
12
2d
¯
42m Tetragonal
No. 122 I
¯
42d
Patterson symmetry I 4/mmm
Origin at
¯
4
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤ 1; 0 ≤ z ≤
1
8
Symmetry operations
For (0,0,0)+ set
(1) 1 (2) 2 0,0,z (3)
¯
4
+
0,0,z;0,0,0(4)
¯
4
−
0,0,z;0,0, 0
(5) 2
1
4
,y,
3
8
(6) 2(
1
2
,0, 0) x,0,
3
8
(7) d(
1
4
,−
1
4
,
3
4
) x +
1
4
, ¯x, z (8) d(
1
4
,
1
4
,
3
4
) x +
1
4
,x,z
For (
1
2
,
1
2
,
1
2
)+ set
(1) t(
1
2
,
1
2
,
1
2
) (2) 2(0,0,
1
2
)
1
4
,
1
4
,z (3)
¯
4
+
1
2
,0, z;
1
2
,0,
1
4
(4)
¯
4
−
0,
1
2
,z;0,
1
2
,
1
4
(5) 2(0,
1
2
,0) 0,y,
1
8
(6) 2 x,
1
4
,
1
8
(7) d(−
1
4
,
1
4
,
1
4
) x +
1
4
, ¯x, z (8) d(
1
4
,
1
4
,
1
4
) x −
1
4
,x,z
428
International Tables for Crystallography (2006). Vol. A, Space group 122, pp. 428–429.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 122 I
¯
42d
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); t(
1
2
,
1
2
,
1
2
); (2); (3); (5)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates
(0,0, 0)+ (
1
2
,
1
2
,
1
2
)+
Reflection conditions
General:
16 e 1(1)x,y,z (2) ¯x, ¯y, z (3) y, ¯x, ¯z (4) ¯y,x, ¯z
(5) ¯x+
1
2
,y, ¯z +
3
4
(6) x +
1
2
, ¯y, ¯z +
3
4
(7) ¯y+
1
2
, ¯x, z +
3
4
(8) y +
1
2
,x,z +
3
4
hkl : h + k + l = 2n
hk0: h + k = 2n
0kl : k + l = 2 n
hhl :2h + l = 4n
00l : l = 4n
h00 : h = 2n
h
¯
h0: h = 2n
Special: as above, plus
8 d . 2 . x,
1
4
,
1
8
¯x,
3
4
,
1
8
1
4
, ¯x,
7
8
3
4
,x,
7
8
no extra conditions
8 c 2 .. 0,0,z 0,0, ¯z
1
2
,0, ¯z +
3
4
1
2
,0, z +
3
4
hkl : l = 2n + 1
or 2h + l = 4n
4 b
¯
4 .. 0,0,
1
2
1
2
,0,
1
4
hkl : l = 2n + 1
or 2h + l = 4n
4 a
¯
4 .. 0,0,0
1
2
,0,
3
4
hkl : l = 2n + 1
or 2h + l = 4n
Symmetry of special projections
Along [001] p4gm
a
=
1
2
(a − b) b
=
1
2
(a + b)
Origin at 0,0,z
Along [100] c2mm
a
= bb
= c
Origin at x,0,
3
8
Along [110] c1m1
a
=
1
2
(−a + b) b
=
1
2
c
Origin at x,x , 0
Maximal non-isomorphic subgroups
I
[2] I
¯
411(I
¯
4, 82) (1; 2; 3; 4)+
[2] I 21d (Fdd2, 43) (1; 2; 7; 8)+
[2] I 221(I 2
1
2
1
2
1
, 24) (1; 2; 5; 6)+
IIa none
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[3] I
¯
42d (c
= 3c) (122); [9] I
¯
42d (a
= 3a,b
= 3b) (122)
Minimal non-isomorphic supergroups
I
[2] I 4
1
/amd (141); [2] I 4
1
/acd (142); [3] I
¯
43d (220)
II [2] C
¯
42d (c
=
1
2
c)(P
¯
4n2, 118)
429
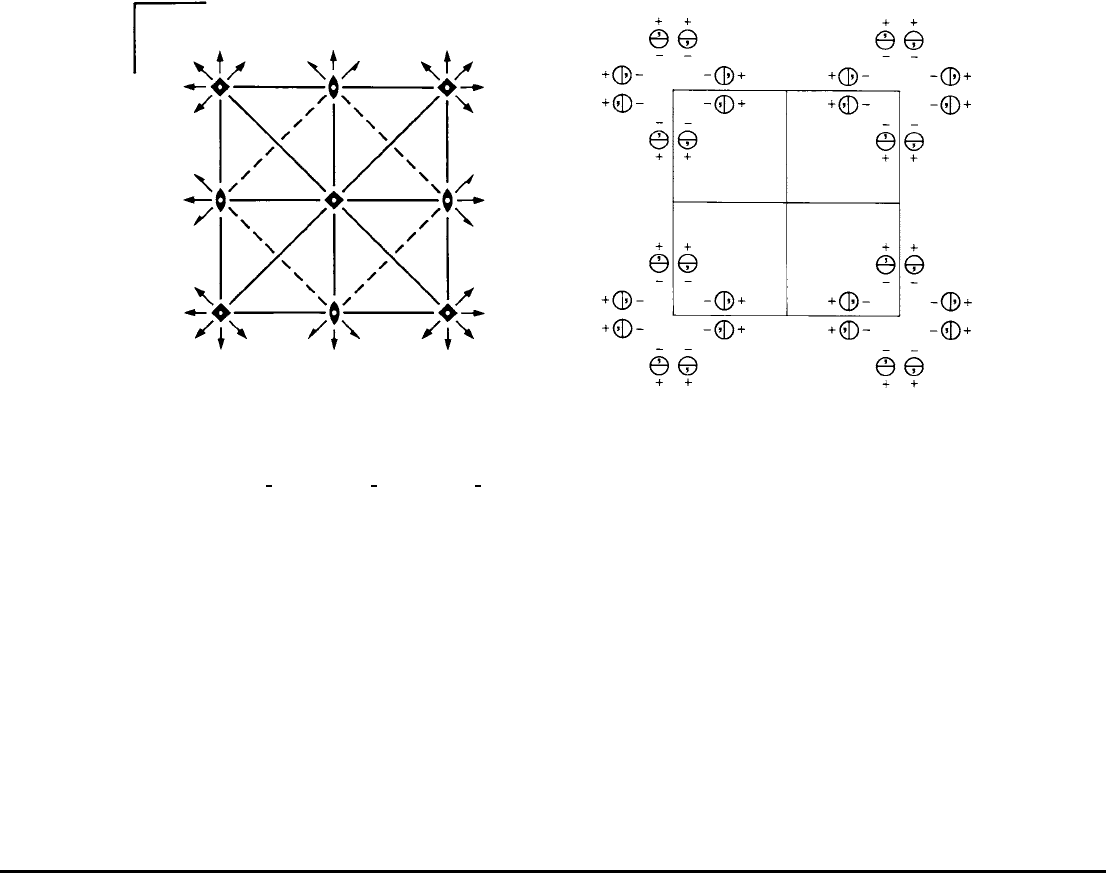
P4/mmm D
1
4h
4/mmm Tetragonal
No. 123 P 4/m 2/m 2/m
Patterson symmetry P4/mmm
Origin at centre (4/mmm)
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
;0≤ z ≤
1
2
; x ≤ y
Symmetry operations
(1) 1 (2) 2 0,0, z (3) 4
+
0,0,z (4) 4
−
0,0,z
(5) 2 0,y, 0(6)2x, 0,0(7)2x, x,0(8)2x, ¯x,0
(9)
¯
10, 0,0 (10) mx, y,0 (11)
¯
4
+
0,0,z;0,0,0 (12)
¯
4
−
0,0,z;0,0, 0
(13) mx,0,z (14) m 0,y,z (15) mx, ¯x,z (16) mx,x, z
Maximal non-isomorphic subgroups
I
[2] P
¯
4m2 (115) 1; 2; 7; 8; 11; 12; 13; 14
[2] P
¯
42m (111) 1; 2; 5; 6; 11; 12; 15; 16
[2] P4mm (99) 1; 2; 3; 4; 13; 14; 15; 16
[2] P422 (89) 1; 2; 3; 4; 5; 6; 7; 8
[2] P4/m11(P4/m, 83) 1; 2; 3; 4; 9; 10; 11; 12
[2] P2/m12/m (Cmmm, 65) 1; 2; 7; 8; 9; 10; 15; 16
[2] P2/m2/m1(Pmmm, 47) 1; 2; 5; 6; 9; 10; 13; 14
IIa none
IIb [2] P4
2
/mcm (c
= 2c) (132); [2] P4
2
/mmc (c
= 2c) (131); [2] P4/mcc(c
= 2c) (124);
[2] C 4/emm (a
= 2a,b
= 2b)(P4/nmm, 129); [2] C4/mmd (a
= 2a,b
= 2b)(P4/mbm, 127);
[2] C 4/emd (a
= 2a,b
= 2b)(P4/nbm, 125); [2] F 4/mmc(a
= 2a,b
= 2b,c
= 2c)(I 4/mcm, 140);
[2] F 4/mmm(a
= 2a,b
= 2b,c
= 2c)(I 4/mmm, 139)
Maximal isomorphic subgroups of lowest index
IIc
[2] P4/mmm(c
= 2c) (123); [2] C4/mmm (a
= 2a,b
= 2b)(P4/mmm, 123)
Minimal non-isomorphic supergroups
I
[3] Pm
¯
3m (221)
II [2] I 4/mmm(139)
430
International Tables for Crystallography (2006). Vol. A, Space group 123, pp. 430–431.
Copyright © 2006 International Union of Crystallography
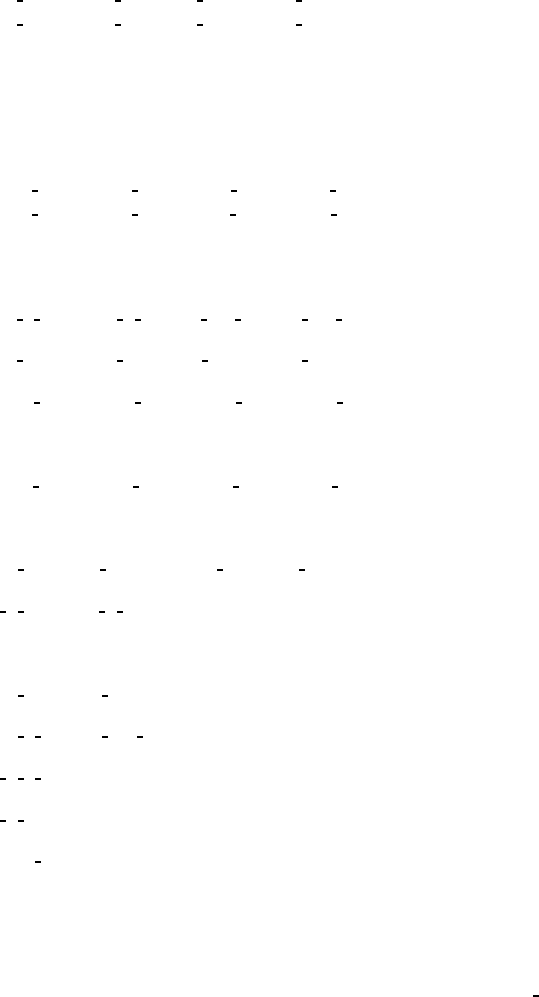
CONTINUED No. 123 P4/mmm
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3); (5); (9)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
16 u 1(1)x,y, z (2) ¯x, ¯y,z (3) ¯y,x,z (4) y, ¯x,z
(5) ¯x,y, ¯z (6) x, ¯y, ¯z (7) y, x, ¯z (8) ¯y, ¯x, ¯z
(9) ¯x, ¯y, ¯z (10) x, y, ¯z (11) y, ¯x, ¯z (12) ¯y,x, ¯z
(13) x, ¯y,z (14) ¯x,y
,z (15) ¯y, ¯x,z (16) y,x,z
no conditions
Special:
8 t . m . x,
1
2
,z ¯x,
1
2
,z
1
2
,x,z
1
2
, ¯x, z
¯x,
1
2
, ¯zx,
1
2
, ¯z
1
2
,x, ¯z
1
2
, ¯x, ¯z
no extra conditions
8 s . m . x,0 , z ¯x,0,z 0,x,z 0, ¯x,z
¯x,0, ¯zx,0, ¯z 0,x, ¯z 0, ¯x, ¯z
no extra conditions
8 r ..mx,x, z ¯x, ¯x,z ¯x,x, zx, ¯x, z
¯x,x, ¯zx, ¯x, ¯zx, x
, ¯z ¯x, ¯x, ¯z
no extra conditions
8 qm.. x,y,
1
2
¯x, ¯y,
1
2
¯y,x,
1
2
y, ¯x,
1
2
¯x,y,
1
2
x, ¯y,
1
2
y, x,
1
2
¯y, ¯x,
1
2
no extra conditions
8 pm.. x,y,0¯x, ¯y, 0¯y,x, 0 y, ¯x,0
¯x,y,0 x , ¯y, 0 y,x,0¯y, ¯x,0
no extra conditions
4 om2 m. x,
1
2
,
1
2
¯x,
1
2
,
1
2
1
2
,x,
1
2
1
2
, ¯x,
1
2
no extra conditions
4 nm2 m. x,
1
2
,0¯x,
1
2
,0
1
2
,x,0
1
2
, ¯x, 0 no extra conditions
4 mm2 m. x,0,
1
2
¯x,0,
1
2
0,x,
1
2
0, ¯x,
1
2
no extra conditions
4 lm2 m. x,0, 0¯x,0,00,x,00, ¯x,0 no extra conditions
4 km. 2mx,x,
1
2
¯x, ¯x,
1
2
¯x,x,
1
2
x, ¯x,
1
2
no extra conditions
4 jm. 2mx,x,0¯x, ¯x,0¯x, x,0 x, ¯x,0 no extra conditions
4 i 2 mm. 0,
1
2
,z
1
2
,0, z 0,
1
2
, ¯z
1
2
,0, ¯zhkl: h + k = 2n
2 h 4 mm
1
2
,
1
2
,z
1
2
,
1
2
, ¯z no extra conditions
2 g 4 mm 0,0,z 0,0, ¯z no extra conditions
2 fmmm. 0,
1
2
,0
1
2
,0, 0 hkl : h + k = 2n
2 emmm. 0,
1
2
,
1
2
1
2
,0,
1
2
hkl : h + k = 2n
1 d 4/mmm
1
2
,
1
2
,
1
2
no extra conditions
1 c 4/mmm
1
2
,
1
2
,0 no extra conditions
1 b 4/ mmm 0,0,
1
2
no extra conditions
1 a 4/ mmm 0,0,0 no extra conditions
Symmetry of special projections
Along [001] p4mm
a
= ab
= b
Origin at 0,0,z
Along [100] p2mm
a
= bb
= c
Origin at x,0,0
Along [110] p2mm
a
=
1
2
(−a + b) b
= c
Origin at x,x , 0
(Continued on preceding page)
431
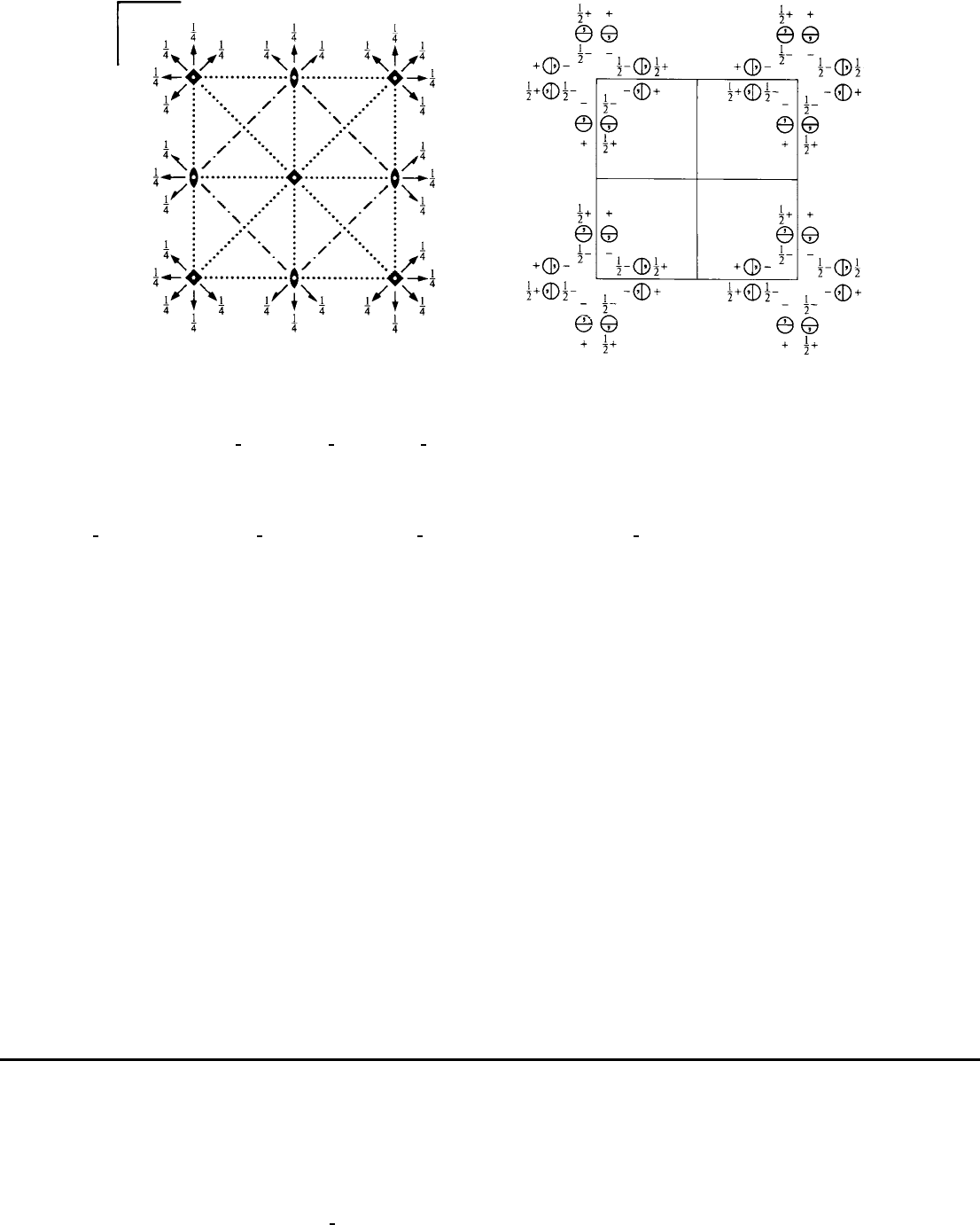
P4/mcc D
2
4h
4/mmm Tetragonal
No. 124 P 4/m 2/c 2/c
Patterson symmetry P4/mmm
Origin at centre (4/m) at 4/mcc
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
;0≤ z ≤
1
4
Symmetry operations
(1) 1 (2) 2 0,0, z (3) 4
+
0,0,z (4) 4
−
0,0,z
(5) 2 0,y,
1
4
(6) 2 x,0,
1
4
(7) 2 x,x,
1
4
(8) 2 x, ¯x,
1
4
(9)
¯
10, 0,0 (10) mx, y,0 (11)
¯
4
+
0,0,z;0,0,0 (12)
¯
4
−
0,0,z;0,0, 0
(13) cx,0,z (14) c 0, y,z (15) cx, ¯x,z (16) cx,x,z
Maximal isomorphic subgroups of lowest index
IIc
[2] C 4/mcc (a
= 2a,b
= 2b)(P4/mcc, 124); [3] P4/mcc(c
= 3c) (124)
Minimal non-isomorphic supergroups
I
none
II [2] I 4/mcm(140); [2] P4/mmm (c
=
1
2
c) (123)
432
International Tables for Crystallography (2006). Vol. A, Space group 124, pp. 432–433.
Copyright © 2006 International Union of Crystallography
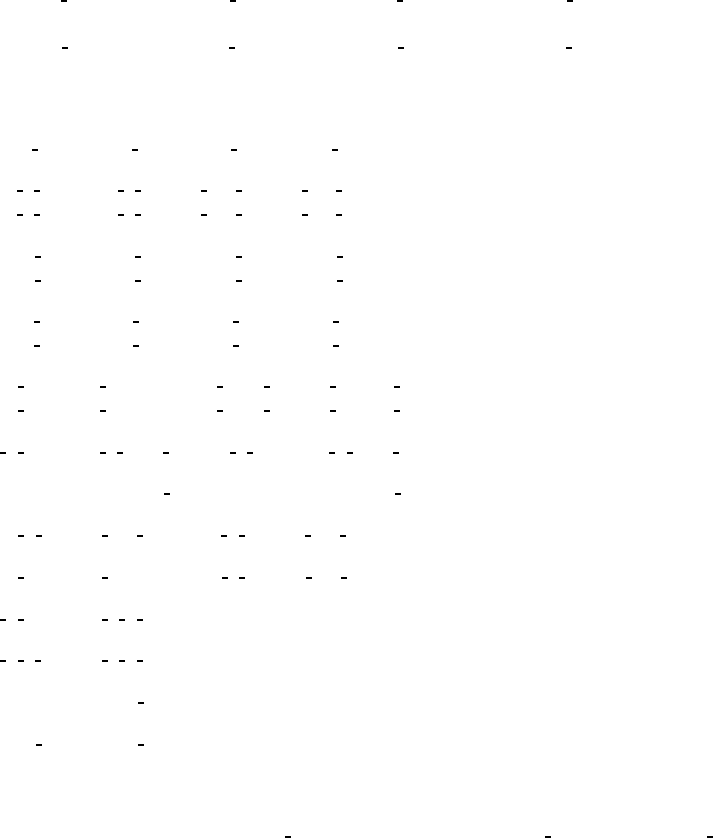
CONTINUED No. 124 P4/mcc
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3); (5); (9)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
16 n 1(1)x,y, z (2) ¯x, ¯y,z (3) ¯y,x, z (4) y, ¯x, z
(5) ¯x,y, ¯z +
1
2
(6) x, ¯y, ¯z +
1
2
(7) y,x, ¯z +
1
2
(8) ¯y, ¯x, ¯z +
1
2
(9) ¯x, ¯y, ¯z (10) x,y, ¯z (11) y, ¯x, ¯z (12) ¯y,x, ¯z
(13) x, ¯y,z +
1
2
(14) ¯x,y, z +
1
2
(15) ¯y, ¯x,z +
1
2
(16) y,x , z +
1
2
0kl : l = 2n
hhl : l = 2n
00l : l = 2n
Special: as above, plus
8 mm.. x,y, 0¯x, ¯y,0¯y,x,0 y, ¯x,0
¯x,y,
1
2
x, ¯y,
1
2
y, x,
1
2
¯y, ¯x,
1
2
no extra conditions
8 l . 2 . x,
1
2
,
1
4
¯x,
1
2
,
1
4
1
2
,x,
1
4
1
2
, ¯x,
1
4
¯x,
1
2
,
3
4
x,
1
2
,
3
4
1
2
, ¯x,
3
4
1
2
,x,
3
4
hkl : l = 2n
8 k . 2 . x,0,
1
4
¯x,0,
1
4
0,x,
1
4
0, ¯x,
1
4
¯x,0,
3
4
x,0,
3
4
0, ¯x,
3
4
0,x,
3
4
hkl : l = 2n
8 j ..2 x,x,
1
4
¯x, ¯x,
1
4
¯x,x,
1
4
x, ¯x,
1
4
¯x, ¯x,
3
4
x,x,
3
4
x, ¯x,
3
4
¯x,x,
3
4
hkl : l = 2n
8 i 2 .. 0,
1
2
,z
1
2
,0, z 0,
1
2
, ¯z +
1
2
1
2
,0, ¯z +
1
2
0,
1
2
, ¯z
1
2
,0, ¯z 0,
1
2
,z +
1
2
1
2
,0, z +
1
2
hkl : h + k,l = 2n
4 h 4 ..
1
2
,
1
2
,z
1
2
,
1
2
, ¯z +
1
2
1
2
,
1
2
, ¯z
1
2
,
1
2
,z +
1
2
hkl : l = 2n
4 g 4 .. 0,0,z 0,0, ¯z+
1
2
0,0, ¯z 0,0 , z +
1
2
hkl : l = 2n
4 f 222. 0,
1
2
,
1
4
1
2
,0,
1
4
0,
1
2
,
3
4
1
2
,0,
3
4
hkl : h + k,l = 2n
4 e 2/m .. 0,
1
2
,0
1
2
,0, 00,
1
2
,
1
2
1
2
,0,
1
2
hkl : h + k,l = 2n
2 d 4/m ..
1
2
,
1
2
,0
1
2
,
1
2
,
1
2
hkl : l = 2n
2 c 422
1
2
,
1
2
,
1
4
1
2
,
1
2
,
3
4
hkl : l = 2n
2 b 4/ m .. 0, 0,00, 0,
1
2
hkl : l = 2n
2 a 422 0,0,
1
4
0,0,
3
4
hkl : l = 2n
Symmetry of special projections
Along [001] p4mm
a
= ab
= b
Origin at 0,0,z
Along [100] p2mm
a
= bb
=
1
2
c
Origin at x,0,0
Along [110] p2mm
a
=
1
2
(−a + b) b
=
1
2
c
Origin at x,x , 0
Maximal non-isomorphic subgroups
I
[2] P
¯
4c2 (116) 1; 2; 7; 8; 11; 12; 13; 14
[2] P
¯
42c (112) 1; 2; 5; 6; 11; 12; 15; 16
[2] P4cc (103) 1; 2; 3; 4; 13; 14; 15; 16
[2] P422 (89) 1; 2; 3; 4; 5; 6; 7; 8
[2] P4/m11(P4/m, 83) 1; 2; 3; 4; 9; 10; 11; 12
[2] P2/m12/c (Cccm, 66) 1; 2; 7; 8; 9; 10; 15; 16
[2] P2/m2/c1(Pccm, 49) 1; 2; 5; 6; 9; 10; 13; 14
IIa none
IIb [2] C 4/ecc (a
= 2a,b
= 2b)(P4/ncc, 130); [2]C4/mcd (a
= 2a,b
= 2b)(P4/mnc, 128);
[2] C 4/ecd (a
= 2a,b
= 2b)(P4/nnc, 126)
(Continued on preceding page)
433
