Hahn Th. (ed.) International tables for crystallography. Vol. A. Space-group symmetry
Подождите немного. Документ загружается.

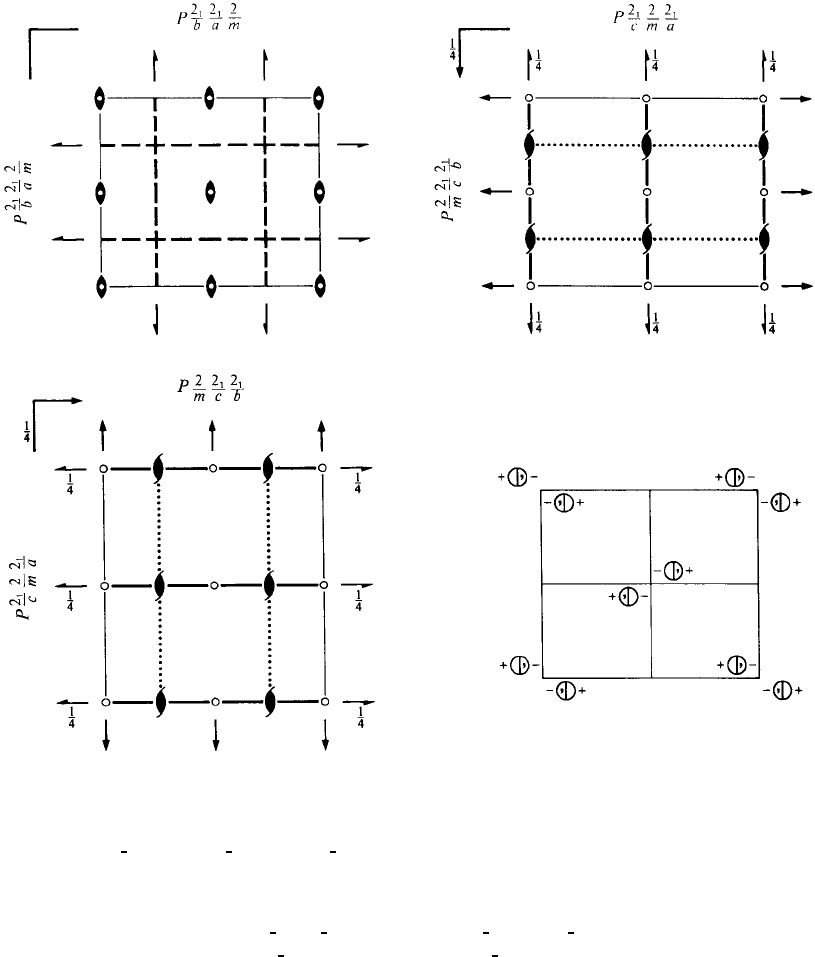
Pbam D
9
2h
mmm Orthorhombic
No. 55 P 2
1
/b 2
1
/a 2/m Patterson symmetry Pmmm
Origin at centre (2/m)
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
;0≤ z ≤
1
2
Symmetry operations
(1) 1 (2) 2 0,0, z (3) 2(0,
1
2
,0)
1
4
,y,0(4)2(
1
2
,0, 0) x,
1
4
,0
(5)
¯
10, 0,0(6)mx,y,0(7)ax,
1
4
,z (8) b
1
4
,y,z
282
International Tables for Crystallography (2006). Vol. A, Space group 55, pp. 282–283.
Copyright © 2006 International Union of Crystallography
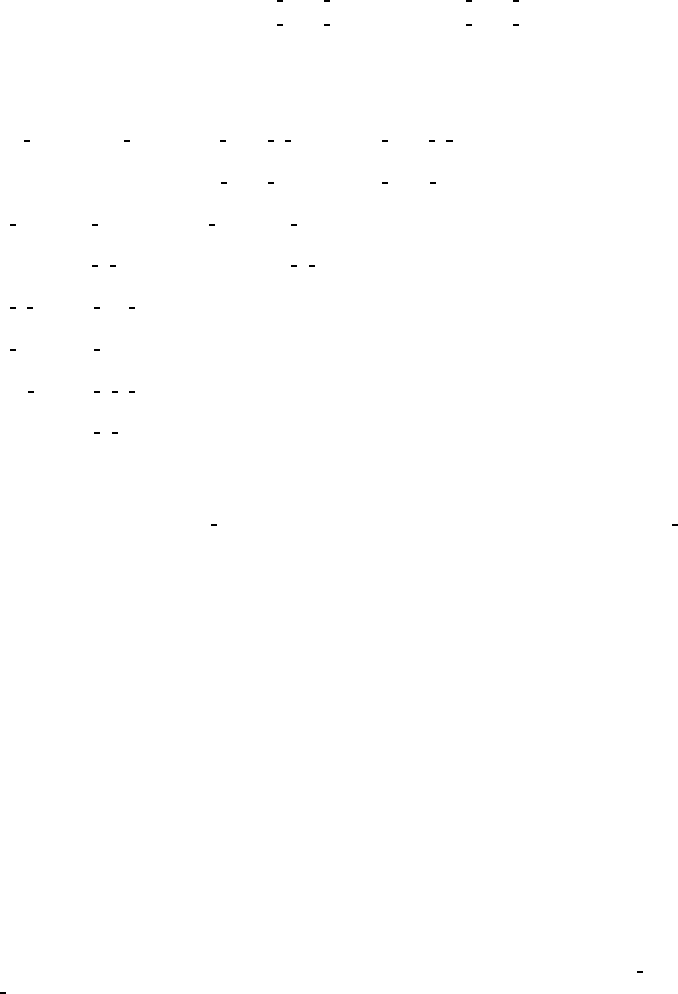
CONTINUED No. 55 Pbam
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3); (5)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
8 i 1(1)x,y,z (2) ¯x, ¯y,z (3) ¯x +
1
2
,y +
1
2
, ¯z (4) x +
1
2
, ¯y +
1
2
, ¯z
(5) ¯x, ¯y, ¯z (6) x, y, ¯z (7) x +
1
2
, ¯y +
1
2
,z (8) ¯x +
1
2
,y +
1
2
,z
0kl : k = 2n
h0l : h = 2n
h00 : h = 2n
0k0: k = 2n
Special: as above, plus
4 h ..mx,y,
1
2
¯x, ¯y,
1
2
¯x+
1
2
,y +
1
2
,
1
2
x +
1
2
, ¯y +
1
2
,
1
2
no extra conditions
4 g ..mx,y, 0¯x, ¯y,0¯x +
1
2
,y +
1
2
,0 x +
1
2
, ¯y +
1
2
,0 no extra conditions
4 f ..20,
1
2
,z
1
2
,0, ¯z 0,
1
2
, ¯z
1
2
,0, zhkl: h + k = 2n
4 e ..20,0,z
1
2
,
1
2
, ¯z 0, 0, ¯z
1
2
,
1
2
,zhkl: h + k = 2n
2 d ..2/m 0,
1
2
,
1
2
1
2
,0,
1
2
hkl : h + k = 2n
2 c ..2/m 0,
1
2
,0
1
2
,0, 0 hkl : h + k = 2n
2 b ..2/m 0,0,
1
2
1
2
,
1
2
,
1
2
hkl : h + k = 2n
2 a ..2/m 0,0, 0
1
2
,
1
2
,0 hkl : h + k = 2n
Symmetry of special projections
Along [001] p2gg
a
= ab
= b
Origin at 0,0,z
Along [100] p2mm
a
=
1
2
bb
= c
Origin at x,0,0
Along [010] p2mm
a
= cb
=
1
2
a
Origin at 0,y, 0
Maximal non-isomorphic subgroups
I
[2] Pba2 (32) 1; 2; 7; 8
[2] Pb2
1
m (Pmc2
1
, 26) 1; 3; 6; 8
[2] P2
1
am (Pmc2
1
, 26) 1; 4; 6; 7
[2] P2
1
2
1
2 (18) 1; 2; 3; 4
[2] P12
1
/a1(P2
1
/c, 14) 1; 3; 5; 7
[2] P2
1
/b11(P2
1
/c, 14) 1; 4; 5; 8
[2] P112/m (P2/m, 10) 1; 2; 5; 6
IIa none
IIb [2] Pnam(c
= 2c)(Pnma, 62); [2] Pbnm(c
= 2c)(Pnma, 62); [2] Pnnm (c
= 2c) (58)
Maximal isomorphic subgroups of lowest index
IIc
[2] Pbam(c
= 2c) (55); [3] Pbam (a
= 3a or b
= 3b) (55)
Minimal non-isomorphic supergroups
I
[2] P4/mbm(127); [2] P4
2
/mbc (135)
II [2] Aeam(Cmce, 64); [2] Bbem (Cmce, 64); [2]Cmmm (65); [2] Ibam (72); [2] Pbmm (a
=
1
2
a)(Pmma, 51);
[2] Pmam(b
=
1
2
b)(Pmma, 51)
283
Pccn D
10
2h
mmm Orthorhombic
No. 56 P 2
1
/c 2
1
/c 2/n Patterson symmetry Pmmm
Origin at
¯
1on11n
Asymmetric unit 0 ≤ x ≤
1
4
;0≤ y ≤ 1; 0 ≤ z ≤
1
2
Symmetry operations
(1) 1 (2) 2
1
4
,
1
4
,z (3) 2(0,
1
2
,0) 0,y,
1
4
(4) 2(
1
2
,0, 0) x,0,
1
4
(5)
¯
10, 0,0(6)n(
1
2
,
1
2
,0) x,y,0(7)cx,
1
4
,z (8) c
1
4
,y,z
284
International Tables for Crystallography (2006). Vol. A, Space group 56, pp. 284–285.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 56 Pccn
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3); (5)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
8 e 1(1)x,y,z (2) ¯x+
1
2
, ¯y +
1
2
,z (3) ¯x,y +
1
2
, ¯z +
1
2
(4) x +
1
2
, ¯y, ¯z +
1
2
(5) ¯x, ¯y, ¯z (6) x +
1
2
,y +
1
2
, ¯z (7) x, ¯y +
1
2
,z +
1
2
(8) ¯x+
1
2
,y,z +
1
2
0kl : l = 2n
h0l : l = 2n
hk0: h + k = 2n
h00 : h = 2n
0k0: k = 2n
00l : l = 2n
Special: as above, plus
4 d ..2
1
4
,
3
4
,z
3
4
,
1
4
, ¯z +
1
2
3
4
,
1
4
, ¯z
1
4
,
3
4
,z +
1
2
hkl : l = 2n
4 c ..2
1
4
,
1
4
,z
3
4
,
3
4
, ¯z +
1
2
3
4
,
3
4
, ¯z
1
4
,
1
4
,z +
1
2
hkl : l = 2n
4 b
¯
10, 0,
1
2
1
2
,
1
2
,
1
2
0,
1
2
,0
1
2
,0, 0 hkl : h + k,h + l, k + l = 2n
4 a
¯
10, 0,0
1
2
,
1
2
,00,
1
2
,
1
2
1
2
,0,
1
2
hkl : h + k,h + l,k + l = 2n
Symmetry of special projections
Along [001] c2mm
a
= ab
= b
Origin at
1
4
,
1
4
,z
Along [100] p2mg
a
= bb
=
1
2
c
Origin at x,0,0
Along [010] p2gm
a
=
1
2
cb
= a
Origin at 0, y,0
Maximal non-isomorphic subgroups
I
[2] Pc2
1
n (Pna2
1
, 33) 1; 3; 6; 8
[2] P2
1
cn (Pna2
1
, 33) 1; 4; 6; 7
[2] Pcc2 (27) 1; 2; 7; 8
[2] P2
1
2
1
2 (18) 1; 2; 3; 4
[2] P12
1
/c1(P2
1
/c, 14) 1; 3; 5; 7
[2] P2
1
/c11 (P2
1
/c, 14) 1; 4; 5; 8
[2] P112/n (P2/ c, 13) 1; 2; 5; 6
IIa none
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[3] Pccn (a
= 3a or b
= 3b) (56); [3] Pccn (c
= 3c) (56)
Minimal non-isomorphic supergroups
I
[2] P4/ncc(130); [2] P4
2
/ncm(138)
II [2] Aema (Cmce, 64); [2] Bmeb (Cmce, 64); [2] Cccm (66); [2] Ibam (72); [2] Pccb (a
=
1
2
a)(Pcca, 54);
[2] Pcca (b
=
1
2
b) (54); [2] Pmmn (c
=
1
2
c) (59)
285
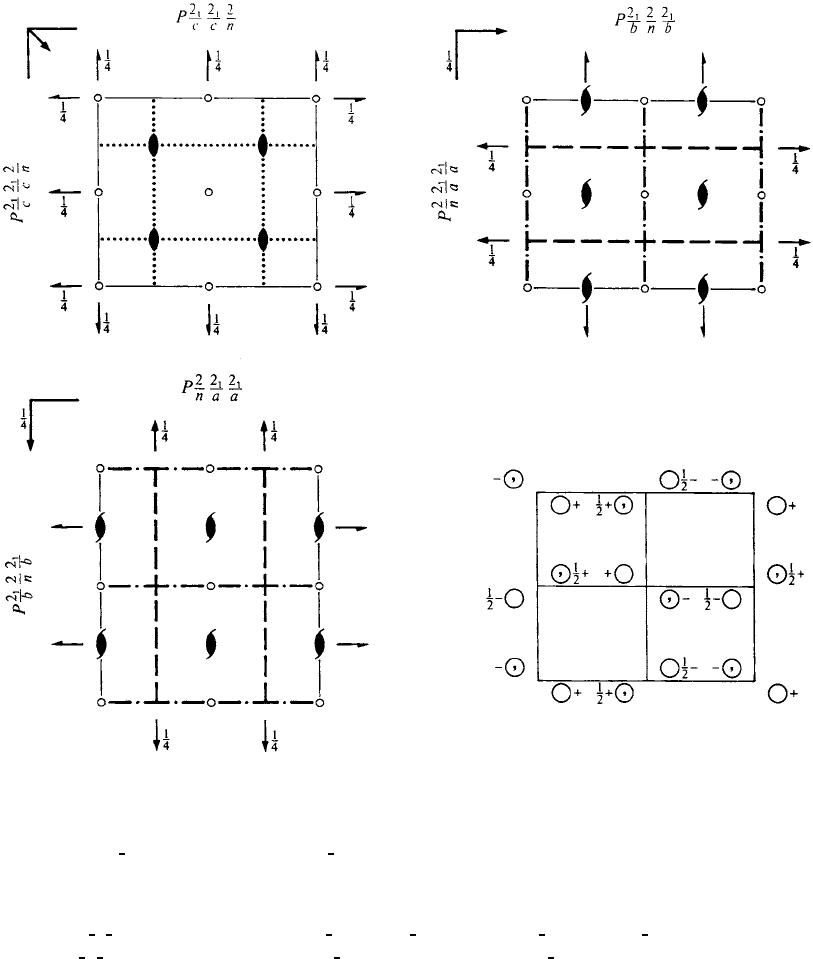
Pbcm D
11
2h
mmm Orthorhombic
No. 57 P 2/b 2
1
/c 2
1
/m Patterson symmetry Pmmm
Origin at
¯
1onb12
1
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤ 1; 0 ≤ z ≤
1
4
Symmetry operations
(1) 1 (2) 2(0, 0,
1
2
) 0,0,z (3) 2(0,
1
2
,0) 0,y,
1
4
(4) 2 x,
1
4
,0
(5)
¯
10, 0,0(6)mx,y,
1
4
(7) cx,
1
4
,z (8) b 0, y,z
286
International Tables for Crystallography (2006). Vol. A, Space group 57, pp. 286–287.
Copyright © 2006 International Union of Crystallography

CONTINUED No. 57 Pbcm
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3); (5)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
8 e 1(1)x,y,z (2) ¯x, ¯y,z +
1
2
(3) ¯x, y +
1
2
, ¯z +
1
2
(4) x, ¯y+
1
2
, ¯z
(5) ¯x, ¯y, ¯z (6) x, y, ¯z +
1
2
(7) x, ¯y+
1
2
,z +
1
2
(8) ¯x,y +
1
2
,z
0kl : k = 2n
h0l : l = 2n
0k0: k = 2n
00l : l = 2n
Special: as above, plus
4 d ..mx,y,
1
4
¯x, ¯y,
3
4
¯x,y +
1
2
,
1
4
x, ¯y +
1
2
,
3
4
no extra conditions
4 c 2 .. x,
1
4
,0¯x,
3
4
,
1
2
¯x,
3
4
,0 x,
1
4
,
1
2
hkl : l = 2n
4 b
¯
1
1
2
,0, 0
1
2
,0,
1
2
1
2
,
1
2
,
1
2
1
2
,
1
2
,0 hkl : k,l = 2n
4 a
¯
10, 0,00,0,
1
2
0,
1
2
,
1
2
0,
1
2
,0 hkl : k, l = 2n
Symmetry of special projections
Along [001] p2gm
a
= ab
= b
Origin at 0,0,z
Along [100] p2gm
a
=
1
2
bb
= c
Origin at x, 0,0
Along [010] p2mm
a
=
1
2
cb
= a
Origin at 0,y, 0
Maximal non-isomorphic subgroups
I
[2] Pbc2
1
(Pca2
1
, 29) 1; 2; 7; 8
[2] P2cm (Pma2, 28) 1; 4; 6; 7
[2] Pb2
1
m (Pmc2
1
, 26) 1; 3; 6; 8
[2] P22
1
2
1
(P2
1
2
1
2, 18) 1; 2; 3; 4
[2] P12
1
/c1(P2
1
/c, 14) 1; 3; 5; 7
[2] P2/b11(P2/c, 13) 1; 4; 5; 8
[2] P112
1
/m (P2
1
/m, 11) 1; 2; 5; 6
IIa none
IIb [2] Pbnm(a
= 2a)(Pnma, 62); [2] Pbca (a
= 2a) (61); [2] Pbna(a
= 2a)(Pbcn, 60)
Maximal isomorphic subgroups of lowest index
IIc
[2] Pbcm (a
= 2a) (57); [3] Pbcm (b
= 3b) (57); [3] Pbcm (c
= 3c) (57)
Minimal non-isomorphic supergroups
I
none
II [2] Cmcm(63); [2] Bbem (Cmce, 64); [2] Aemm (Cmme, 67); [2] Ibam(72); [2] Pmcm (b
=
1
2
b)(Pmma, 51);
[2] Pbmm (c
=
1
2
c)(Pmma, 51)
287
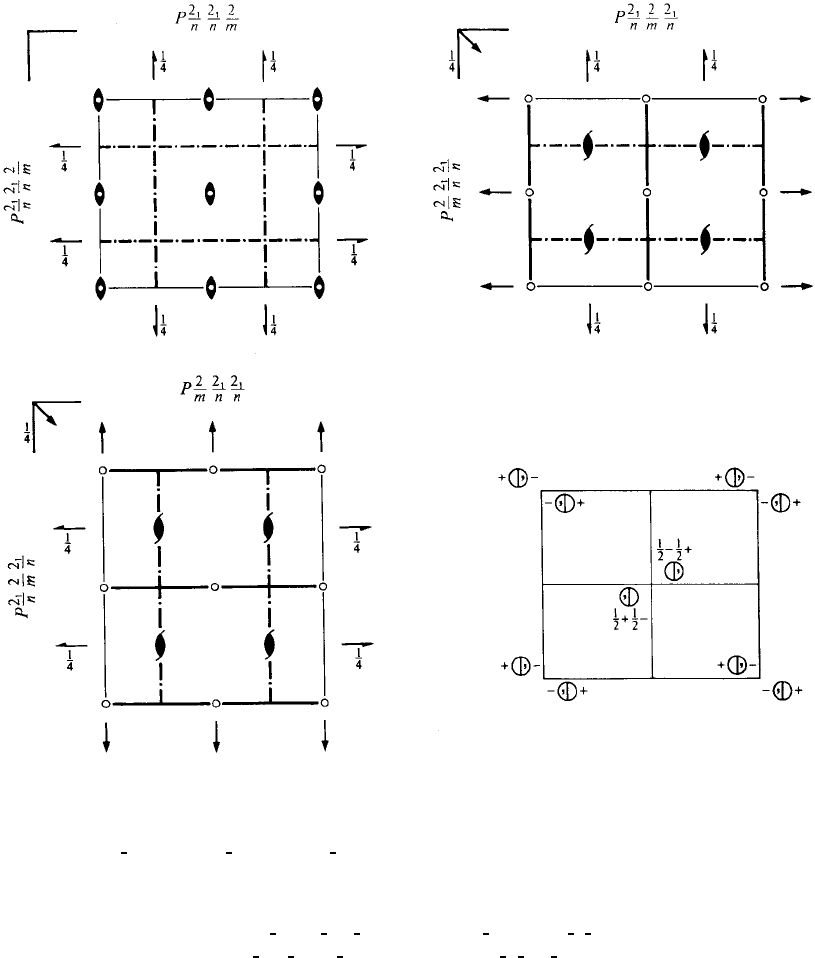
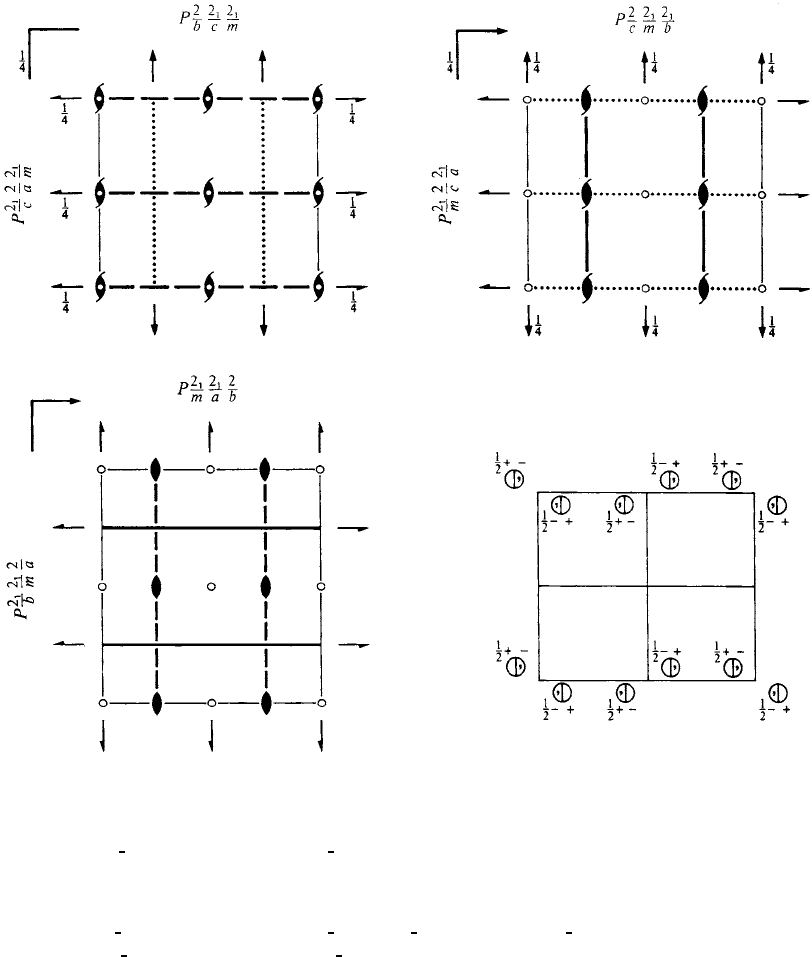
Pnnm D
12
2h
mmm Orthorhombic
No. 58 P 2
1
/n 2
1
/n 2/m Patterson symmetry Pmmm
Origin at centre (2/m)
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
;0≤ z ≤
1
2
Symmetry operations
(1) 1 (2) 2 0,0, z (3) 2(0,
1
2
,0)
1
4
,y,
1
4
(4) 2(
1
2
,0, 0) x,
1
4
,
1
4
(5)
¯
10, 0,0(6)mx,y,0(7)n(
1
2
,0,
1
2
) x,
1
4
,z (8) n(0,
1
2
,
1
2
)
1
4
,y,z
288
International Tables for Crystallography (2006). Vol. A, Space group 58, pp. 288–289.
Copyright © 2006 International Union of Crystallography
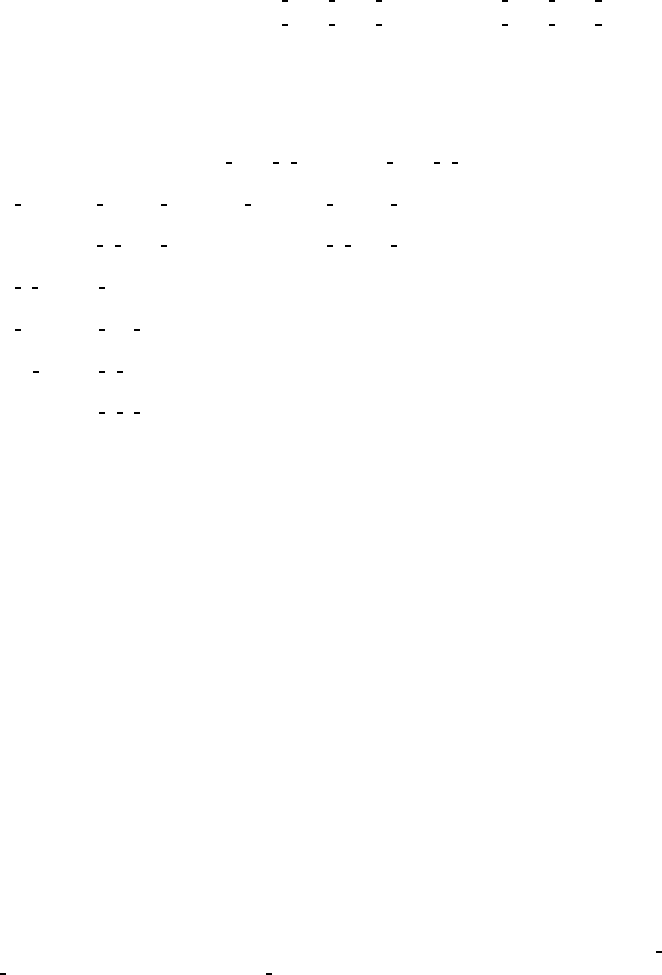
CONTINUED No. 58 Pnnm
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3); (5)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
8 h 1(1)x, y,z (2) ¯x, ¯y, z (3) ¯x +
1
2
,y +
1
2
, ¯z +
1
2
(4) x +
1
2
, ¯y +
1
2
, ¯z +
1
2
(5) ¯x, ¯y, ¯z (6) x, y, ¯z (7) x +
1
2
, ¯y +
1
2
,z +
1
2
(8) ¯x +
1
2
,y +
1
2
,z +
1
2
0kl : k + l = 2 n
h0l : h + l = 2n
h00 : h = 2n
0k0: k = 2n
00l : l = 2n
Special: as above, plus
4 g ..mx,y, 0¯x, ¯y,0¯x +
1
2
,y +
1
2
,
1
2
x +
1
2
, ¯y +
1
2
,
1
2
no extra conditions
4 f ..20,
1
2
,z
1
2
,0, ¯z +
1
2
0,
1
2
, ¯z
1
2
,0, z +
1
2
hkl : h + k + l = 2n
4 e ..20,0,z
1
2
,
1
2
, ¯z +
1
2
0,0, ¯z
1
2
,
1
2
,z +
1
2
hkl : h + k + l = 2n
2 d ..2/m 0,
1
2
,
1
2
1
2
,0, 0 hkl : h + k + l = 2n
2 c ..2/m 0,
1
2
,0
1
2
,0,
1
2
hkl : h + k + l = 2n
2 b ..2/m 0,0,
1
2
1
2
,
1
2
,0 hkl : h + k + l = 2n
2 a ..2/m 0,0, 0
1
2
,
1
2
,
1
2
hkl : h + k + l = 2n
Symmetry of special projections
Along [001] p2gg
a
= ab
= b
Origin at 0,0,z
Along [100] c2mm
a
= bb
= c
Origin at x,0,0
Along [010] c2mm
a
= cb
= a
Origin at 0,y, 0
Maximal non-isomorphic subgroups
I
[2] Pnn2 (34) 1; 2; 7; 8
[2] Pn2
1
m (Pmn2
1
, 31) 1; 3; 6; 8
[2] P2
1
nm (Pmn2
1
, 31) 1; 4; 6; 7
[2] P2
1
2
1
2 (18) 1; 2; 3; 4
[2] P12
1
/n1(P2
1
/c, 14) 1; 3; 5; 7
[2] P2
1
/n11(P2
1
/c, 14) 1; 4; 5; 8
[2] P112/m (P2/m, 10) 1; 2; 5; 6
IIa none
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[3] Pnnm(a
= 3a or b
= 3b) (58); [3] Pnnm(c
= 3c) (58)
Minimal non-isomorphic supergroups
I
[2] P4/mnc(128); [2] P4
2
/mnm (136)
II [2] Amam(Cmcm, 63); [2] Bbmm (Cmcm, 63); [2] Cccm (66); [2] Immm (71); [2] Pncm (a
=
1
2
a)(Pmna, 53);
[2] Pcnm(b
=
1
2
b)(Pmna, 53); [2] Pbam(c
=
1
2
c) (55)
289
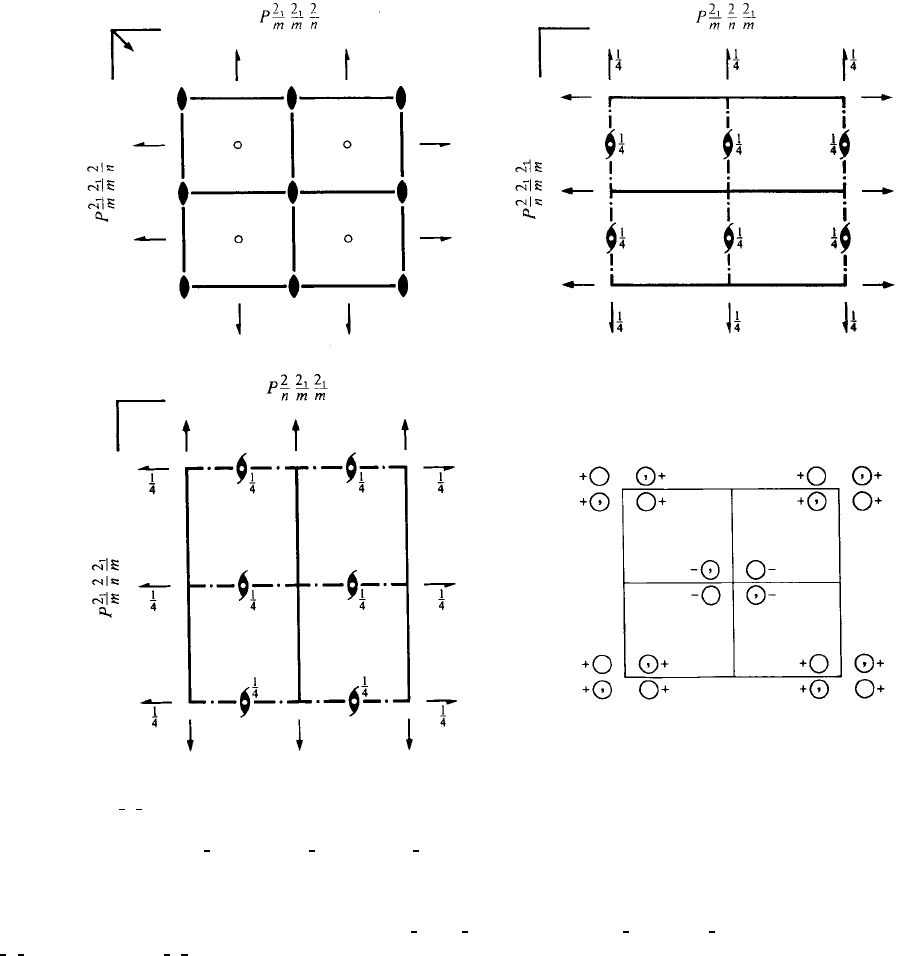
Pmmn D
13
2h
mmm Orthorhombic
No. 59 P 2
1
/m 2
1
/m 2 /n Patterson symmetry Pmmm
ORIGIN CHOICE 1
Origin at mm2/n,at
1
4
,
1
4
,0 from
¯
1
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
;0≤ z ≤
1
2
Symmetry operations
(1) 1 (2) 2 0,0,z (3) 2(0,
1
2
,0)
1
4
,y,0(4)2(
1
2
,0, 0) x,
1
4
,0
(5)
¯
1
1
4
,
1
4
,0(6)n(
1
2
,
1
2
,0) x, y,0(7)mx,0 , z (8) m 0,y,z
290
International Tables for Crystallography (2006). Vol. A, Space group 59, pp. 290–293.
Copyright © 2006 International Union of Crystallography
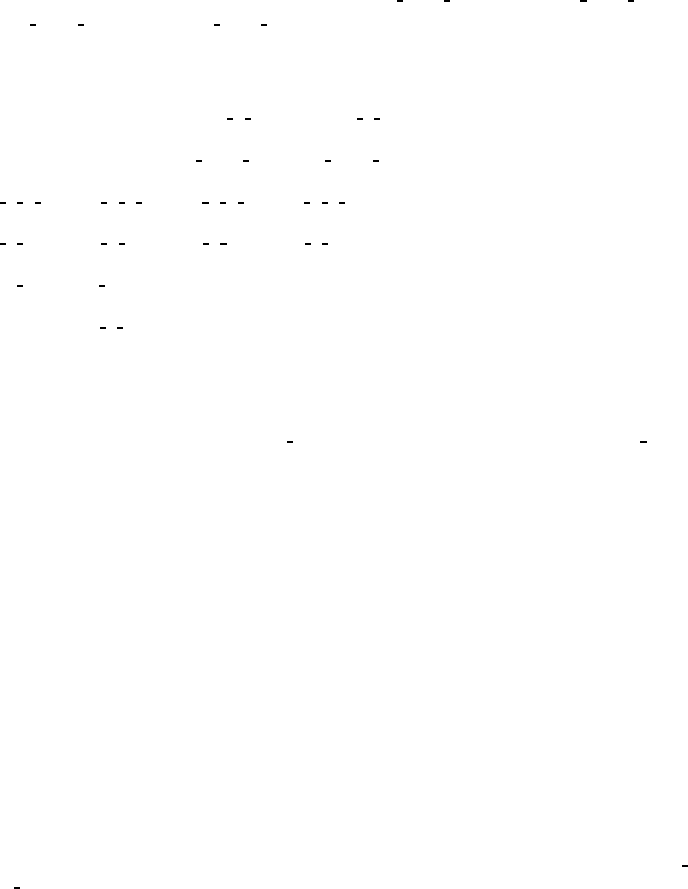
CONTINUED No. 59 Pmmn
Generators selected (1); t(1, 0,0); t(0,1,0); t(0,0,1); (2); (3); (5)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
8 g 1(1)x,y,z (2) ¯x, ¯y,z (3) ¯x +
1
2
,y +
1
2
, ¯z (4) x +
1
2
, ¯y +
1
2
, ¯z
(5) ¯x+
1
2
, ¯y +
1
2
, ¯z (6) x +
1
2
,y +
1
2
, ¯z (7) x, ¯y,z (8) ¯x,y,z
hk0: h + k = 2n
h00 : h = 2n
0k0: k = 2n
Special: as above, plus
4 f . m . x,0, z ¯x,0, z ¯x+
1
2
,
1
2
, ¯zx+
1
2
,
1
2
, ¯z no extra conditions
4 em.. 0,y,z 0, ¯y,z
1
2
,y +
1
2
, ¯z
1
2
, ¯y +
1
2
, ¯z no extra conditions
4 d
¯
1
1
4
,
1
4
,
1
2
3
4
,
3
4
,
1
2
1
4
,
3
4
,
1
2
3
4
,
1
4
,
1
2
hkl : h,k = 2n
4 c
¯
1
1
4
,
1
4
,0
3
4
,
3
4
,0
1
4
,
3
4
,0
3
4
,
1
4
,0 hkl : h,k = 2n
2 bmm20,
1
2
,z
1
2
,0, ¯z no extra conditions
2 amm20, 0,z
1
2
,
1
2
, ¯z no extra conditions
Symmetry of special projections
Along [001] c2mm
a
= ab
= b
Origin at 0,0,z
Along [100] p2mg
a
= bb
= c
Origin at x,
1
4
,0
Along [010] p2gm
a
= cb
= a
Origin at
1
4
,y,0
Maximal non-isomorphic subgroups
I
[2] Pm2
1
n (Pmn2
1
, 31) 1; 3; 6; 8
[2] P2
1
mn (Pmn2
1
, 31) 1; 4; 6; 7
[2] Pmm2 (25) 1; 2; 7; 8
[2] P2
1
2
1
2 (18) 1; 2; 3; 4
[2] P112/n (P2/c, 13) 1; 2; 5; 6
[2] P12
1
/m1(P2
1
/m, 11) 1; 3; 5; 7
[2] P2
1
/m11 (P2
1
/m, 11) 1; 4; 5; 8
IIa none
IIb [2] Pcmn (c
= 2c)(Pnma, 62); [2] Pmcn (c
= 2c)(Pnma, 62); [2] Pccn (c
= 2c) (56)
Maximal isomorphic subgroups of lowest index
IIc
[2] Pmmn (c
= 2c) (59); [3] Pmmn (a
= 3a or b
= 3b) (59)
Minimal non-isomorphic supergroups
I
[2] P4/nmm(129); [2] P4
2
/nmc(137)
II [2] Amma (Cmcm, 63); [2] Bmmb (Cmcm, 63); [2] Cmmm (65); [2] Immm (71); [2] Pmmb (a
=
1
2
a)(Pmma, 51);
[2] Pmma (b
=
1
2
b) (51)
291
