Hahn Th. (ed.) International tables for crystallography. Vol. A. Space-group symmetry
Подождите немного. Документ загружается.

the P cell, origin O, by the linear transformation
a
0
a b, b
0
a b, c
0
c
and the shift
p
1
4
a
1
4
b:
The matrices P, p and P are thus given by
P
1
10
110
001
0
@
1
A
, p
1
4
1
4
0
0
@
1
A
, P
1
10
1
4
110
1
4
0010
0001
0
B
B
@
1
C
C
A
:
From Fig. 5.2.3.1, we derive also the inverse transformation
a
1
2
a
0
1
2
b
0
, b
1
2
a
0
1
2
b
0
, c c
0
, q
1
4
a
0
:
Thus, the matrices Q, q and Q are
Q P
1
1
2
1
2
0
1
2
1
2
0
001
0
B
@
1
C
A
, q P
1
p
1
4
0
0
0
B
@
1
C
A
,
Q P
1
1
2
1
2
0
1
4
1
2
1
2
00
0010
0001
0
B
B
B
B
@
1
C
C
C
C
A
:
The coordinates x, y, z of points in the P cell are transformed by Q:
x
0
y
0
z
0
1
0
B
B
B
B
@
1
C
C
C
C
A
=
1
2
1
2
0
1
4
1
2
1
2
00
0010
0001
0
B
B
B
B
@
1
C
C
C
C
A
x
y
z
1
0
B
B
B
B
@
1
C
C
C
C
A
=
1
2
x y
1
4
1
2
x y
z
1
0
B
B
B
B
@
1
C
C
C
C
A
:
The coordinate triplets of the four silicon positions in the P cell
are 0.300, 0.300, 0; 0.700, 0.700,
1
2
; 0.200, 0.800,
1
4
; 0.800, 0.200,
3
4
.
Four triplets in the C cell are obtained by inserting these values into
the equation just derived. The new coordinates are 0.050, 0, 0;
0.450, 0,
1
2
; 0.250, 0.300,
1
4
; 0.250, 0.300,
3
4
. A set of four further
points is obtained by adding the centring translation
1
2
,
1
2
, 0 to these
coordinates.
The indices h, k, l are transformed by the matrix P :
h
0
, k
0
, l
0
h, k, l
1
10
110
001
0
@
1
A
h k, h k, l,
i.e. the reflections with the indices h, k, l of the P cell become
reflections h k, h k, l of the C cell.
The symmetry operations of space group P4
1
2
1
2 are listed in the
space-group tables for the P cell as follows:
1 x, y, z; 2
x,
y,
1
2
z;
3
1
2
y,
1
2
x,
1
4
z; 4
1
2
y,
1
2
x,
3
4
z;
5
1
2
x,
1
2
y,
1
4
z; 6
1
2
x,
1
2
y,
3
4
z;
7 y, x,z; 8
y,
x,
1
2
z:
The corresponding matrices W are
1
1000
0100
0010
0001
0
B
B
B
@
1
C
C
C
A
; 2
1000
0
100
001
1
2
0001
0
B
B
B
@
1
C
C
C
A
; 3
0
10
1
2
100
1
2
001
1
4
0001
0
B
B
B
@
1
C
C
C
A
;
4
010
1
2
100
1
2
001
3
4
0001
0
B
B
B
@
1
C
C
C
A
; 5
100
1
2
010
1
2
00
1
1
4
0001
0
B
B
B
@
1
C
C
C
A
; 6
100
1
2
0
10
1
2
00
1
3
4
0001
0
B
B
B
@
1
C
C
C
A
;
7
0100
1000
00
10
0001
0
B
B
B
@
1
C
C
C
A
; 8
0
100
1000
00
1
1
2
0001
0
B
B
B
@
1
C
C
C
A
:
These matrices of the P cell are transformed to the matrices W
0
of
the C cell by
W
0
QWP:
For matrix (2), for example, this results in
W
0
1
2
1
2
0
1
4
1
2
1
2
00
0010
0001
0
B
B
B
B
@
1
C
C
C
C
A
1000
0
100
001
1
2
0001
0
B
B
B
@
1
C
C
C
A
1
10
1
4
110
1
4
0010
0001
0
B
B
B
@
1
C
C
C
A
100
1
2
0
100
001
1
2
0001
0
B
B
B
@
1
C
C
C
A
:
The eight transformed matrices W
0
, derived in this way, are
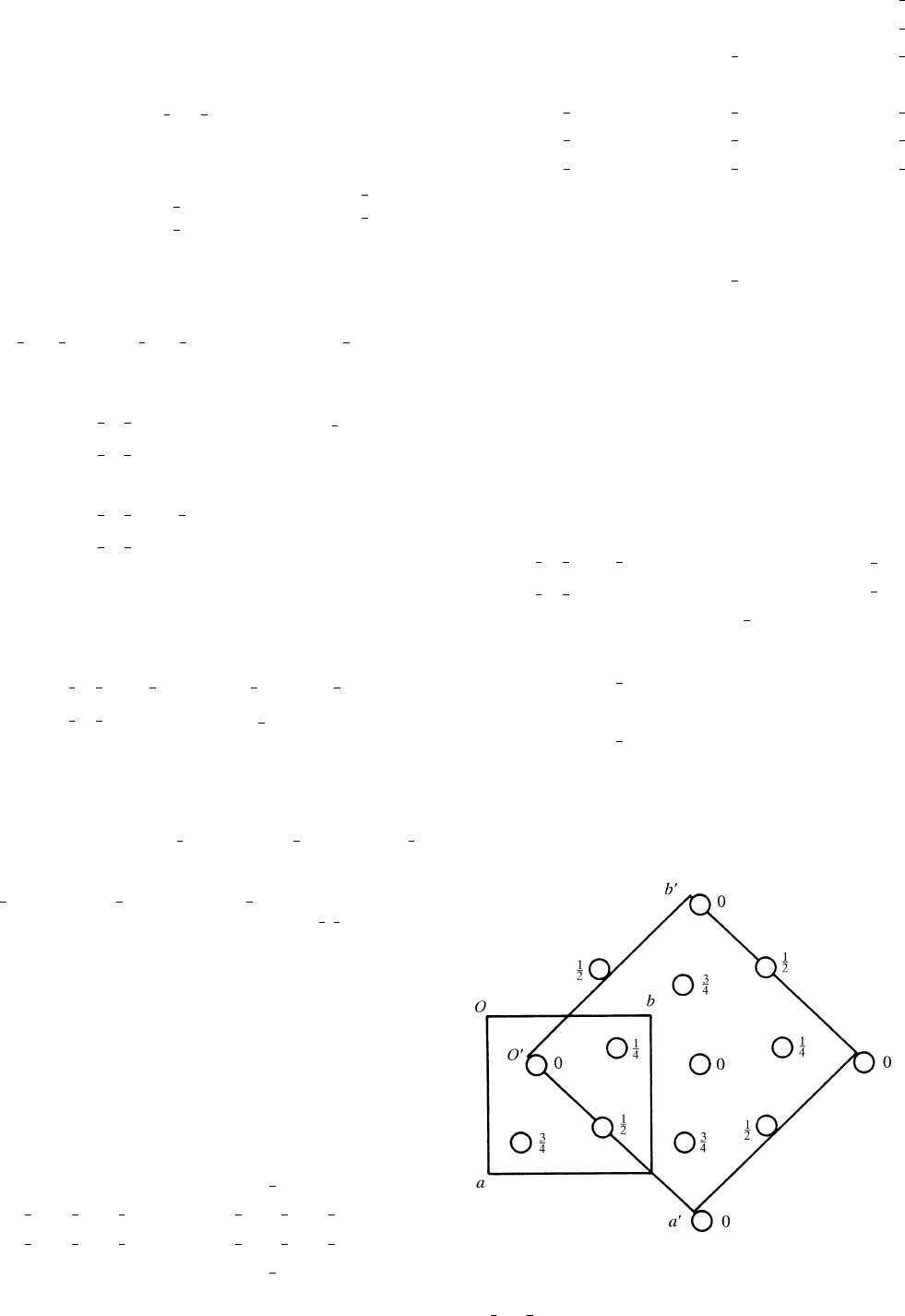
Fig. 5.2.3.1. Positions of silicon atoms in the low-cristobalite structure,
projected along 00
1. Primitive tetragonal cell a, b, c; C-centred
tetragonal cell a
0
, b
0
, c
0
. Shift of origin from O to O
0
by the vector
p
1
4
a
1
4
b.
88
5. TRANSFORMATIONS IN CRYSTALLOGRAPHY
1
1000
0100
0010
0001
0
B
B
B
@
1
C
C
C
A
; 2
100
1
2
0
100
001
1
2
0001
0
B
B
B
@
1
C
C
C
A
; 3
0
10
1
4
100
1
4
001
1
4
0001
0
B
B
B
@
1
C
C
C
A
;
4
010
1
4
100
1
4
001
3
4
0001
0
B
B
B
B
@
1
C
C
C
C
A
; 5
010
1
4
100
1
4
00
1
1
4
0001
0
B
B
B
@
1
C
C
C
A
; 6
0
10
1
4
100
1
4
00
1
3
4
0001
0
B
B
B
B
@
1
C
C
C
C
A
;
7
1000
0
100
00
10
0001
0
B
B
B
@
1
C
C
C
A
; 8
100
1
2
0100
00
1
1
2
0001
0
B
B
B
@
1
C
C
C
A
:
Another set of eight matrices is obtained by adding the C-centring
translation
1
2
,
1
2
, 0 to the w’s.
From these matrices, one obtains the coordinates of the general
position in the C cell, for instance from matrix (2)
~
x
~
y
~z
1
0
B
B
@
1
C
C
A
100
1
2
0
100
001
1
2
0001
0
B
B
@
1
C
C
A
x
y
z
1
0
B
B
@
1
C
C
A
x
1
2
y
z
1
2
1
0
B
B
@
1
C
C
A
:
The eight points obtained by the eight matrices W
0
are
1 x, y, z; 2
1
2
x,
y,
1
2
z;
3
1
4
y,
1
4
x,
1
4
z; 4
1
4
y,
1
4
x,
3
4
z;
5
1
4
y,
1
4
x,
1
4
z; 6
1
4
y,
1
4
x,
3
4
z;
7 x,
y,z; 8
1
2
x, y,
1
2
z:
The other set of eight points is obtained by adding
1
2
,
1
2
,0.
In space group P4
1
2
1
2, the silicon atoms are in special position
4(a) ..2 with the coordinates x, x, 0. Transformed into the C cell, the
position becomes
0, 0, 0
1
2
,
1
2
,0
x,0,0;
1
2
x,0,
1
2
;
1
4
,
1
4
x,
1
4
;
1
4
,
3
4
x,
3
4
:
The parameter x 0:300 of the P cell has changed to x 0:050 in
the C cell. For x 0, the special position of the C cell assumes the
same coordinate triplets as Wyckoff position 8(a)
43m in space
group Fd
3m (227), i.e. this change of the x parameter reflects the
displacement of the silicon atoms in the cubic to tetragonal phase
transition.
References
5.2
Altmann, S. L. & Herzig, P. (1994). Point-Group Theory Tables.
Oxford Science Publications.
International Tables for Crystallography (2004). Vol. C, edited
by E. Prince, Table 8.3.1.1. Dordrecht: Kluwer Academic
Publishers.
Megaw, H. D. (1973). Crystal structures: a working approach, pp.
259–262. Philadelphia: Saunders.
Nieuwenkamp, W. (1935). Die Kristallstruktur des Tief-Cristobalits
SiO
2
. Z. Kristallogr. 92, 82–88.
Wyckoff, R. W. G. (1925). Die Kristallstruktur von -Cristobalit
SiO
2
(bei hohen Temperaturen stabile Form). Z. Kristallogr. 62,
189–200.
89
5.2. TRANSFORMATIONS OF SYMMETRY OPERATIONS
references
p1 1 Oblique
No. 1 p1
Patterson symmetry p2
Origin arbitrary
Asymmetric unit 0 ≤ x ≤ 1; 0 ≤ y ≤ 1
Symmetry operations
(1) 1
Generators selected (1); t(1, 0); t(0,1)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
1 a 1(1)x,y no conditions
Maximal non-isomorphic subgroups
I
none
IIa none
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[2] p 1(a
= 2a or b
= 2b or a
= a+ b,b
= −a + b)(1)
Minimal non-isomorphic supergroups
I
[2] p 2 (2); [2] pm (3); [2] pg (4); [2] cm (5); [3] p3 (13)
II none
92
International Tables for Crystallography (2006). Vol. A, Plane group 1, p. 92.
Copyright © 2006 International Union of Crystallography
Oblique 2 p2
Patterson symmetry p2 p2No.2
Origin at 2
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤ 1
Symmetry operations
(1) 1 (2) 2 0,0
Generators selected (1); t(1, 0); t(0,1); (2)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
2 e 1(1)x,y (2) ¯x, ¯y no conditions
Special: no extra conditions
1 d 2
1
2
,
1
2
1 c 2
1
2
,0
1 b 20,
1
2
1 a 20,0
Maximal non-isomorphic subgroups
I
[2] p 1(1) 1
IIa none
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[2] p 2(a
= 2a or b
= 2b or a
= a+ b,b
= −a + b)(2)
Minimal non-isomorphic supergroups
I
[2] p 2mm(6); [2] p2mg (7); [2] p2gg (8); [2] c 2mm (9); [2] p4 (10); [3] p6 (16)
II none
93
International Tables for Crystallography (2006). Vol. A, Plane group 2, p. 93.
Copyright © 2006 International Union of Crystallography
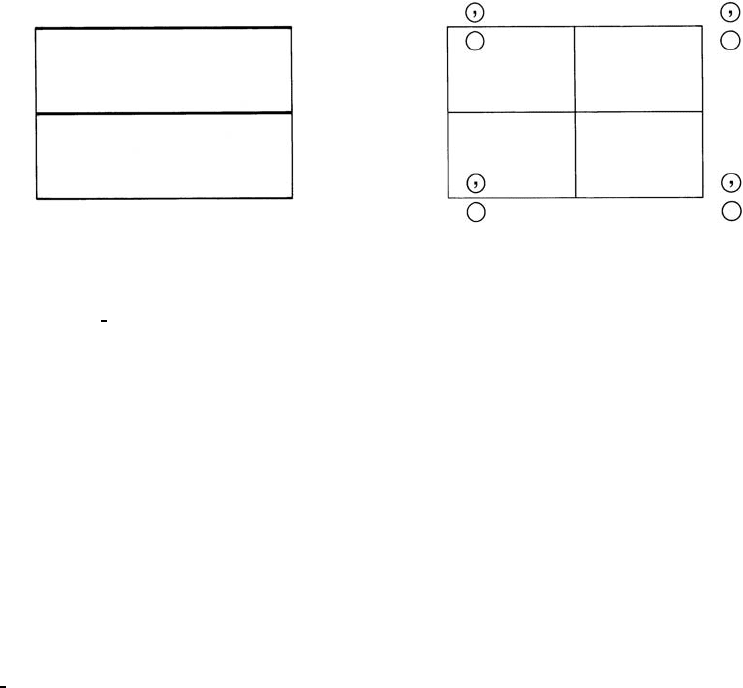
pm m Rectangular
No. 3 p1m1
Patterson symmetry p2mm
Origin on m
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤ 1
Symmetry operations
(1) 1 (2) m 0, y
Generators selected (1); t(1, 0); t(0,1); (2)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
2 c 1(1)x,y (2) ¯x,y no conditions
Special: no extra conditions
1 b . m .
1
2
,y
1 a . m . 0,y
Maximal non-isomorphic subgroups
I
[2] p 1(1) 1
IIa none
IIb [2] pg (b
= 2b) (4); [2] cm(a
= 2a,b
= 2b)(5)
Maximal isomorphic subgroups of lowest index
IIc
[2] pm (a
= 2a) (3); [2] pm(b
= 2b)(3)
Minimal non-isomorphic supergroups
I
[2] p 2mm(6); [2] p2mg (7)
II [2] cm(5)
94
International Tables for Crystallography (2006). Vol. A, Plane group 3, p. 94.
Copyright © 2006 International Union of Crystallography
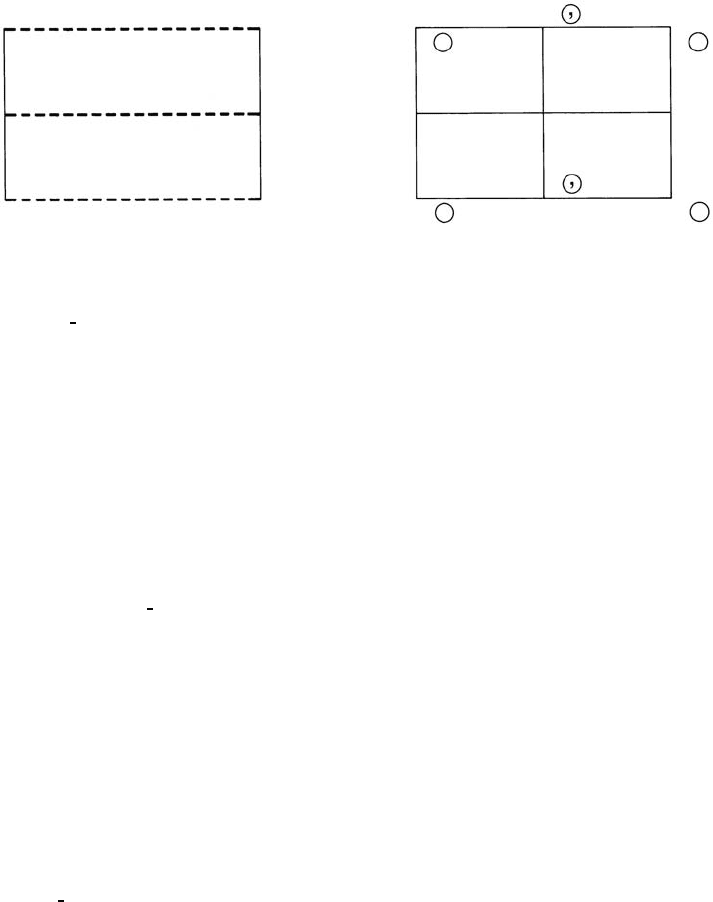
Rectangular m pg
Patterson symmetry p2mm p1g1No.4
Origin on g
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤ 1
Symmetry operations
(1) 1 (2) b 0,y
Generators selected (1); t(1, 0); t(0,1); (2)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
2 a 1(1)x,y (2) ¯x,y +
1
2
0k: k = 2n
Maximal non-isomorphic subgroups
I
[2] p 1(1) 1
IIa none
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[2] pg (a
= 2a) (4); [3] pg(b
= 3b)(4)
Minimal non-isomorphic supergroups
I
[2] p 2mg(7); [2] p2 gg (8)
II [2] cm(5); [2] pm (b
=
1
2
b)(3)
95
International Tables for Crystallography (2006). Vol. A, Plane group 4, p. 95.
Copyright © 2006 International Union of Crystallography

cm m Rectangular
No. 5 c1m1
Patterson symmetry c2mm
Origin on m
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
Symmetry operations
For (0,0)+ set
(1) 1 (2) m 0,y
For (
1
2
,
1
2
)+ set
(1) t(
1
2
,
1
2
) (2) b
1
4
,y
Generators selected (1); t(1, 0); t(0,1); t(
1
2
,
1
2
); (2)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates
(0,0)+ (
1
2
,
1
2
)+
Reflection conditions
General:
4 b 1(1)x,y (2) ¯x,yhk: h + k = 2n
h0: h = 2n
0k: k = 2n
Special: no extra conditions
2 a . m . 0,y
Maximal non-isomorphic subgroups
I
[2] c1(p1, 1) 1+
IIa [2] pg (4) 1; 2 +(
1
2
,
1
2
)
[2] pm (3) 1; 2
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[3] cm (a
= 3a) (5); [3] cm (b
= 3b)(5)
Minimal non-isomorphic supergroups
I
[2] c2mm (9); [3] p3m1 (14); [3] p31m (15)
II [2] pm (a
=
1
2
a,b
=
1
2
b)(3)
96
International Tables for Crystallography (2006). Vol. A, Plane group 5, p. 96.
Copyright © 2006 International Union of Crystallography
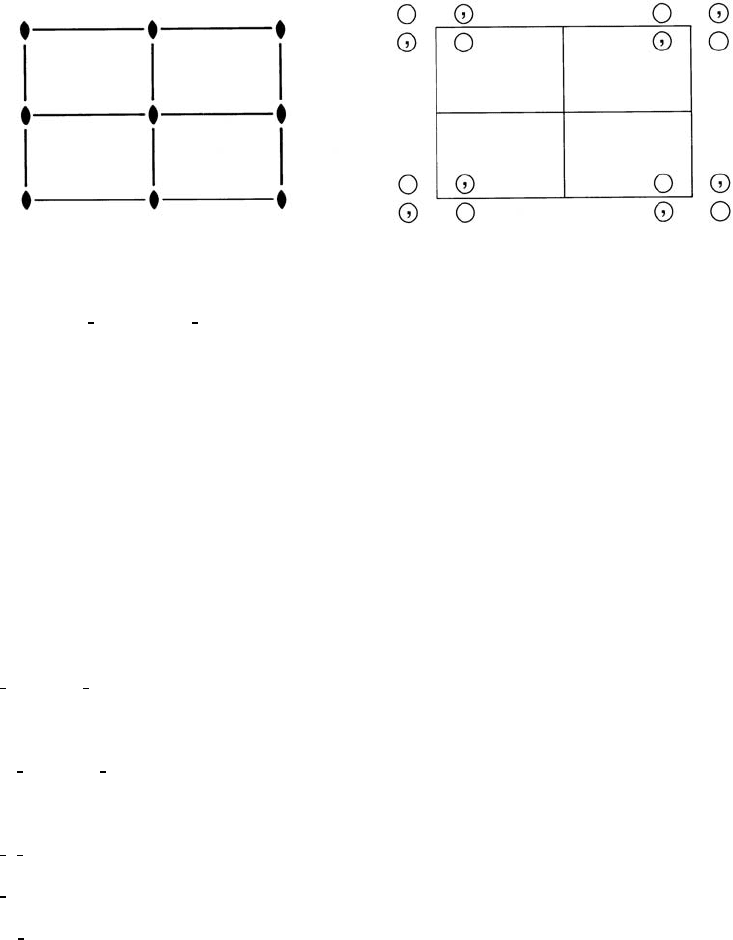
Rectangular 2mm p2mm
Patterson symmetry p2mm p2mm No. 6
Origin at 2mm
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
Symmetry operations
(1) 1 (2) 2 0,0(3)m 0,y (4) mx, 0
Generators selected (1); t(1, 0); t(0,1); (2); (3)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
4 i 1(1)x, y (2) ¯x, ¯y (3) ¯x,y (4) x, ¯y no conditions
Special: no extra conditions
2 h . m .
1
2
,y
1
2
, ¯y
2 g . m . 0,y 0, ¯y
2 f ..mx,
1
2
¯x,
1
2
2 e ..mx,0¯x,0
1 d 2 mm
1
2
,
1
2
1 c 2 mm
1
2
,0
1 b 2 mm 0,
1
2
1 a 2 mm 0,0
Maximal non-isomorphic subgroups
I
[2] p 1m1(pm,3) 1; 3
[2] p 11m (pm,3) 1; 4
[2] p 211 (p2, 2) 1; 2
IIa none
IIb [2] p2mg(a
= 2a) (7); [ 2] p2gm (b
= 2b)(p 2mg,7);[2]c2mm(a
= 2a,b
= 2b)(9)
Maximal isomorphic subgroups of lowest index
IIc
[2] p 2mm( a
= 2a or b
= 2b)(6)
Minimal non-isomorphic supergroups
I
[2] p 4mm(11)
II [2] c2mm (9)
97
International Tables for Crystallography (2006). Vol. A, Plane group 6, p. 97.
Copyright © 2006 International Union of Crystallography

p2mg 2mm Rectangular
No. 7 p2mg
Patterson symmetry p2mm
Origin at 21g
Asymmetric unit 0 ≤ x ≤
1
4
;0≤ y ≤ 1
Symmetry operations
(1) 1 (2) 2 0,0(3)m
1
4
,y (4) ax,0
Generators selected (1); t(1, 0); t(0,1); (2); (3)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
4 d 1(1)x,y (2) ¯x, ¯y (3) ¯x +
1
2
,y (4) x +
1
2
, ¯yh0: h = 2n
Special: as above, plus
2 c . m .
1
4
,y
3
4
, ¯y no extra conditions
2 b 2 .. 0,
1
2
1
2
,
1
2
hk: h = 2n
2 a 2 .. 0,0
1
2
,0 hk: h = 2n
Maximal non-isomorphic subgroups
I
[2] p 11g (pg,4) 1; 4
[2] p 1m1(pm,3) 1; 3
[2] p 211 (p2, 2) 1; 2
IIa none
IIb [2] p2gg(b
= 2b)(8)
Maximal isomorphic subgroups of lowest index
IIc
[2] p 2mg( b
= 2b) (7); [3] p2mg(a
= 3a)(7)
Minimal non-isomorphic supergroups
I
none
II [2] c2mm (9); [2] p2mm(a
=
1
2
a)(6)
98
International Tables for Crystallography (2006). Vol. A, Plane group 7, p. 98.
Copyright © 2006 International Union of Crystallography
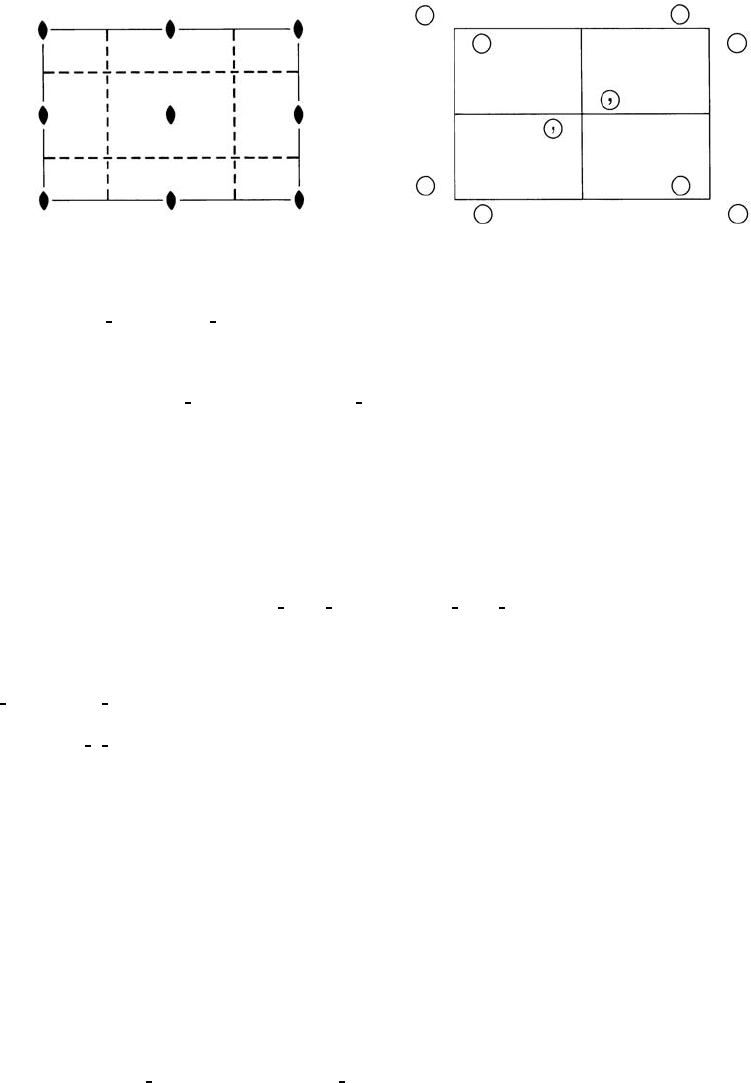
Rectangular 2mm p2gg
Patterson symmetry p2mm p2gg No. 8
Origin at 2
Asymmetric unit 0 ≤ x ≤
1
2
;0≤ y ≤
1
2
Symmetry operations
(1) 1 (2) 2 0,0(3)b
1
4
,y (4) ax,
1
4
Generators selected (1); t(1, 0); t(0,1); (2); (3)
Positions
Multiplicity,
Wyckoff letter,
Site symmetry
Coordinates Reflection conditions
General:
4 c 1(1)x,y (2) ¯x, ¯y (3) ¯x +
1
2
,y +
1
2
(4) x+
1
2
, ¯y+
1
2
h0: h = 2n
0k: k = 2n
Special: as above, plus
2 b 2 ..
1
2
,00,
1
2
hk: h + k = 2n
2 a 2 .. 0,0
1
2
,
1
2
hk: h + k = 2n
Maximal non-isomorphic subgroups
I
[2] p 1g1(pg,4) 1; 3
[2] p 11g (pg,4) 1; 4
[2] p 211 (p2, 2) 1; 2
IIa none
IIb none
Maximal isomorphic subgroups of lowest index
IIc
[3] p 2gg( a
= 3a or b
= 3b)(8)
Minimal non-isomorphic supergroups
I
[2] p 4gm(12)
II [2] c2mm (9); [2] p2mg(a
=
1
2
a) (7); [2] p2gm(b
=
1
2
b)(p2mg,7)
99
International Tables for Crystallography (2006). Vol. A, Plane group 8, p. 99.
Copyright © 2006 International Union of Crystallography
