Громкович Ю. Теоретическая информатика. Введение в теорию автоматов, теорию вычислимости, теорию сложности, теорию алгоритмов, рандомизацию, теорию связи и криптографию
Подождите немного. Документ загружается.


D
K
w E
K
(w)
D
K
(w) w
E
K
(w) K
E
B
(D
K
(w)) B
(w, E
B
(D
K
(w)))
B (w, E
B
(D
K
(w))) K
B
B B
K
C K E
K
(u)
u B
B u
B D
K
K
B E
K
(w) (w, E
B
(D
K
(w)))
K E
K
(u) B
E
K
(w) = E
K
(u) u B
C K C
E
C
(D
K
(w)) u
B
K
B 0
K B
NP
L ∈ NP
x ∈ L |x|
NP
23
C K
24

MT
MT L
x
|x|
x ∈ L
x ∈ L
|x|
x ∈ L
L ⊆ Σ
∗
Σ
L
V x ∈ Σ
∗
• x ∈ L B V
B x 2/3
x ∈ L
V
B
• x /∈ L B V B
V x
2/3
x /∈ L x ∈ L
V x ∈ L
25
26
27
28
29
x ∈ L x ∈ Σ
∗

IP
IP = { L ⊆ Σ
∗
| L }.
O(|x|)
2
−|x|
IP 2/3
1 − 2
−|x|
NP ⊆ IP
NP = VP
L ∈ NP L
x ∈ L c x ∈ L
c |x|
c
c x ∈ L x /∈ L
x ∈ L
ut
NP
G
1
G
2
NP
NP
NP
NONISO = {(G
1
, G
2
) | G
1
G
2
}.
NONISO (G
1
G
2
) V B
V G
1
G
2
V
1
G
1
G
2
V
i ∈ {1, 2} (j
1
, j
2
, . . . , j
n
)
(1, 2, . . . , n) n V G
i
30
31
i

G
i
(j
1
, j
2
, . . . , j
n
) V
G
i
(j
1
, j
2
, . . . , j
n
) B
G
i
(j
1
, j
2
, . . . , j
n
) G
1
G
2
G
1
G
2
B i
G
1
G
2
G
i
(j
1
, j
2
, . . . , j
n
) i
V
G
1
G
2
B
i B i B
k ∈ {1, 2} V
k 6= i V (G
1
, G
2
)
k = i V s ∈ {1, 2}
G
s
B B l ∈ {1, 2} V
l 6= s V (G
1
, G
2
)
k = s V (G
1
, G
2
)
NONISO
(G
1
, G
2
) ∈ NO NISO
G
1
G
2
(G
1
, G
2
)
1
(G
1
, G
2
) /∈ NONISO
G
1
G
2
i s
{1, 2}
1
2
·
1
2
=
1
4
1/4 2
−k
k
∗
IP = P SPACE ut
x ∈ L L ∈ PSPACE
|x|
32
L ∈ PSPACE
x ∈ L

B V
V
M
V
f(x, y) y
B x V V
x
NP
(G
1
, G
2
) B V n G
1
G
2
B i ∈ {1, 2}
π = (j
1
, j
2
, . . . , j
n
) (1, 2, . . . , n) B π G
i
G
i
(π)
V j ∈ {1, 2}
j
G
i
(π) G
j
B G
1
G
2
δ
G
j
(δ) = G
i
(π) δ
G
1
G
2
i = j
δ = π i 6= j
G
j
G
i
(π)
π
33

V (G
1
, G
2
) G
j
(δ) = G
i
(π)
G
1
G
2
δ G
j
(δ) = G
i
(π) V
(G
1
, G
2
) 1 G
1
G
2
i = j B δ G
j
(δ) = G
i
(π)
i = j i, j ∈ {1, 2}
1/2 k
2
−k
B V
G
1
G
2
G
i
(π)
i π j δ
π δ π
π G
1
G
2
(G
1
, G
2
)
(G
i
(π), j, δ) B V
(G
i
(π), j, δ)
2n
x
0
, x
1
, . . . , x
n−1
, y
0
, y
1
, . . . , y
n−1
,
2n x
x
0
, x
1
, . . . , x
n−1
y y
0
, y
1
, . . . , y
n−1
x
34
35
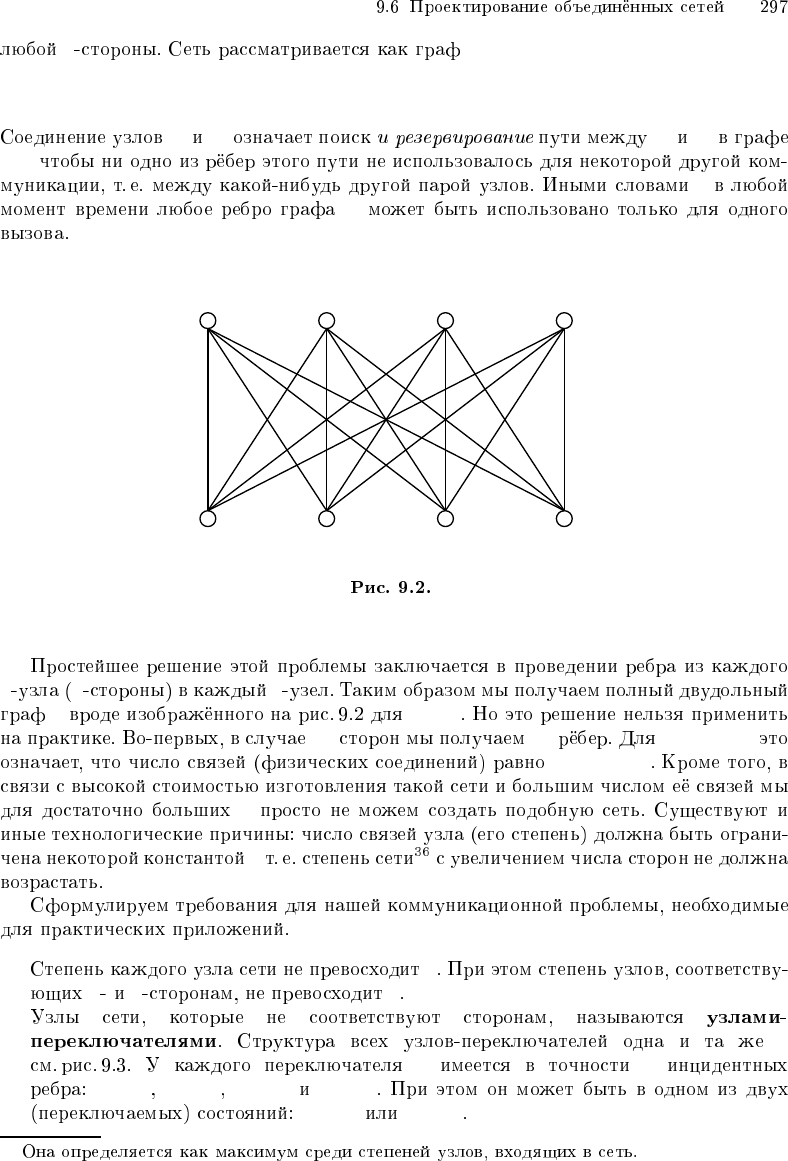
y
G = (V, E), x
0
, x
1
, . . . , x
n−1
, y
0
, y
1
, . . . , y
n−1
∈ V.
x
i
y
j
x
i
y
j
G
G
x
0
x
1
x
2
x
3
y
0
y
1
y
2
y
3
x x y
n = 4
2n n
2
n = 10 0 00
100 000 000
n
• 4
x y 2
•
v 4
LO (v) L U (v) RO(v) RU(v)
LLRR LRRL
36

LO(v)LO(v)
LU(v)LU (v)
RO(v)RO(v)
RU(v)RU ( v)
v LLR R v
LRRL
v LLRR
v LO (v) LU(v)
RO(v) RU(v) LO(v) LU (v)
RO(v)
RU(v)
v LRRL v
LO (v) RU(v) RO(v) LU(v)
LO (v) RU(v)
RO(v) LU(v)
• u x
u L(u) R(u) u
2 L R
x
0
x
1
x
2
x
3
y
0
y
1
y
2
y
3
(0, 00)
(1, 00)
(2, 00)
(0, 01)
(1, 01)
(2, 01)
(0, 10)
(1, 10)
(2, 10)
(0, 11)
(1, 11)
(2, 11)
37
y

•
(i
0
, i
1
, . . . , i
n−1
)
(0, 1, . . . , n − 1) j ∈ {0, 1, . . . , n − 1}
x x
j
y y
i
j
n! (i
0
, i
1
, . . . , i
n−1
)
n
(x
0
, y
i
0
), (x
1
, y
i
1
), . . . , (x
n−1
, y
i
n−1
).
n
x
j
y
i
j
j = 0, 1, . . . , n −1
2n
x
0
, x
1
, . . . , x
n−1
, y
0
, y
1
, . . . , y
n−1
,
(0, 1, . . . , n − 1) n
x y
2n
4n
8
4
4
x y 2
(3, 0, 2, 1)
4
38
L R x LLRR LRRL
39
40
x
i
y
i
41

2n Ω(n log n)
n n ∈ IN
Ω(n log n)
Net
n
n
Net
n
m N et
n
Net
n
2
n
·2
m
.
2
m
·2
n
≥ n! 2
m
≥
n!
2
n
.
m ≥ log
2
(n!) − n ≥ n · log n − n · (ln e + 1) ∈ Ω(n log n).
ut
n
x y
log
2
n
n
n O(n log n)
r β
r β r r
But
r
= (V
r
, E
r
)
V
r
= {(i, w) | i ∈ {0, 1, . . . , r}, w ∈ {0, 1}
r
},
E
r
= {{(i, w), (i + 1, w)} | i ∈ {0, 1, . . . , r − 1}}∪
{{(i, xay), (i + 1, xby)} | i ∈ {0, 1, . . . , r − 1}, x ∈ {0, 1}
i
,
a, b ∈ {0, 1}, a 6= b, y ∈ {0, 1}
r−i−1
}.
1 β But
1
42
43
Net
n
n! n
44
n! ≈
n
n
e
n
·
√
2πn
