Грименицкий П.Н., Лабутин Н.А. Расчет параметров настройки цифровых регуляторов. Учебное пособие для студентов специальности Автоматизация технологических процессов и производств
Подождите немного. Документ загружается.


с информацией об изменении динамики объекта [1]. Введение запаса устойчи-
вости по ограничению на максимум АЧХ рассматривалось в [3].
Выведем формулы для расчета запаса устойчивости по ограничению на
расположение корней характеристического уравнения, конкретно — по ограни-
чению на m — степень колебательности. Для этого используем математический
аппарат D- разбиения [2].
Характеристическое уравнение замкнутой дискретно-непрерывной АСР
имеет вид:
(6. 1)
,0)z(W1
pc
=
+
(6. 2)
),z(WW)z(W)z(W
дмppc μ
⋅
=
— Z - преобразование произведения соответствующих импульсных
)z(WW
дмμ
характеристик объекта управления и демодулятора [5].
Пусть
,ееz
TjTm
ω
ω
−
⋅= (6. 3)
тогда выражение (2.2) примет вид:
(6. 4)
),j,T,m(WW)j,T,m(W)j,T,m(W
дмppc
ω
⋅
ω
=ω
μ
Вывод формул начнем с наиболее общего случая — дискретного ПИД-
алгоритма регулирования, КЧХ которого записывается следующим образом:
Т
е1
К
е1
T
КK)j,T,m(W
TjTm
д
TjTm
ипpc
ω+
ω
−
ω+ω−
−
+
−
+=ω
. (6. 5)
Расширенную КЧХ объекта управления представим через мнимую и дей-
ствительную составляющие:
(6. 6)
),,T,m(JJj),T,m(RR)j,T,m(WW
дмдмдм
ω
+
ω
=ω
μμμ
и учтем, что
(6. 7) .TsinjTcosе
Tj
ω−ω=
ω−
Подставив (6. 4 — 6. 7) в (6. 2) и приравняв к нулю действительную и
мнимую составляющие, получим систему из двух уравнений:
30

(
)
[]
(
)
[]
01Tsinе),T,m(JJTcosе1),T,m(RR
T
1
K
Tsinе),T,m(JJTcosе1),T,m(RR
еTcosе21
T
К),T,m(RRK
Tm
дм
Tm
дмд
Tm
дм
Tm
дм
Tm2Tm
идмп
=+ωω−ω−ω+
+ωω+ω−ω×
×
+ω−
+ω
ω
μ
ω
μ
ω
μ
ω
μ
ωω
μ
(
)
[]
(
)
[]
0Tcosе1),T,m(JJTsinе),T,m(RR
Tsinе),T,m(RRTcosе1),T,m(JJ
еTcosе21
T
К),T,m(JJK
Tm
дм
Tm
дм
Tm
дм
Tm
дм
Tm2Tm
идмп
=ω−ω+ωω+
+ωω−ω−ω×
×
+ω−
+ω
ω
μ
ω
μ
ω
μ
ω
μ
ωω
μ
Решив приведенную систему уравнений относительно К
31
п
и К , получим
и
формулы для границы заданного запаса устойчивости по критерию m, выра-
женные через расширенные вещественную и мнимую комплексные частотные
характеристики дискретного объекта управления:
(
)
(
)
(
)
;еTcosе21
1
K
),T,m(JJ),T,m(RRTsinе
еTcosе21),T,m(JJ
T
1
),T,m(K
Tm2Tm
2
T
д
2
дм
2
дм
Tm
Tm2Tm
дм
и
ωω
μμ
ω
ω
ω
μ
+ω−+
+
ω+ωω
+ω−ω
⋅−=ω
(6. 8)
(
)
(
)
(
)
.Tcosе1
1
K2
),T,m(JJ),T,m(RRTsinе
Tcosе1),T,m(JJTsinе),T,m(RR
),T,m(K
Tm
T
д
2
дм
2
дм
Tm
Tm
дм
Tm
дм
п
ω−−
−
ω+ωω
ω−ω−ωω
=
=ω
ω
μμ
ω
ω
μ
ω
μ
(6. 9)
Формулы (6. 8) и (6. 9) можно переписать через расширенные амплитуд-
но-частотную и фазочастотную характеристики, используя известные выраже-
ния [2]:
(6. 10)
),T,m(cos),T,m(AA),T,m(RR
дмдмдм
ωϕϕ⋅ω=ω
μμμ
(6. 11)
),T,m(sin),T,m(AA),T,m(JJ
дмдмдм
ωϕϕ⋅ω−=ω
μμμ

Тогда
()
,еTcosе21
1
K
),T,m(AA
),T,m(sin
Tsinе
еTcosе21
T
1
),T,m(K
Tm2Tm
2
T
д
дм
дм
Tm
Tm2Tm
и
ωω
μ
μ
ω
ω
ω
+ω−+
+
ω
ωϕϕ
ω
+ω−
=ω
(6. 12)
()
.Tcosе1
1
K2
),T,m(ATAsinе
)Tcosе1(),T,m(sin
),T,m(ATAsinе
Тsinе),T,m(cos
),T,m(K
Tm
T
д
дм
Tm
Tm
дм
дм
Tm
Tm
дм
п
ω−−
−
ωω
ω−ωϕϕ
+
+
ωω
ωωϕϕ
−=ω
ω
μ
ω
ω
μ
μ
ω
ω
μ
(6. 13)
Из (6. 8) и (6. 9) можно получить формулы для ПИ- и ПД-алгоритмов
регулирования как частных случаев формул ПИД-алгоритма.
ПИ-алгоритм:
(
)
(
)
;
),T,m(JJ),T,m(RRTsinе
еTcosе21),T,m(JJ
T
1
),T,m(K
2
дм
2
дм
Tm
Tm2Tm
дм
и
ω+ωω
+ω−ω
⋅−=ω
μμ
ω
ω
ω
μ
(6. 14)
()
()
),T,m(JJ),T,m(RRTsinе
Tcosе1),T,m(JJTsinе),T,m(RR
),T,m(K
2
дм
2
дм
Tm
Tm
дм
Tm
дм
п
ω+ωω
ω−ω−ωω
=
=ω
μμ
ω
ω
μ
ω
μ
(6. 15)
или
;
),T,m(AA
),T,m(sin
Tsinе
еTcosе21
T
1
),T,m(K
дм
дм
Tm
Tm2Tm
и
ω
ωϕϕ
ω
+ω−
=ω
μ
μ
ω
ω
ω
(6. 16)
.
),T,m(AATsinе
)Tcosе1(),T,m(sin
),T,m(AATsinе
Тsinе),T,m(cos
),T,m(K
дм
Tm
Tm
дм
дм
Tm
Tm
дм
п
ω⋅ω
ω−ωϕϕ
+
+
ω⋅ω
ωωϕϕ
−=ω
μ
ω
ω
μ
μ
ω
ω
μ
(6. 17)
32

ПД-алгоритм:
(
)
;
),T,m(JJ),T,m(RRTsin
),T,m(JJТе
),T,m(K
2
дм
2
дм
дм
Tm
д
ω+ωω
ω
=ω
μμ
μ
ω
−
(6. 18)
(
)
,
Tsin
Tcosе),T,m(JJ
),T,m(RR
),T,m(JJ),T,m(RR
1
),T,m(K
Tm
дм
дм
2
дм
2
дм
п
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
ω
ω−ω
+ω×
×
ω+ω
=ω
ω−
μ
μ
μμ
(6. 19)
;
Tsin),T,m(AA
),T,m(sinТе
),T,m(K
дм
дм
Tm
д
ωω
ωϕϕ
=ω
μ
μ
ω
−
(6. 20)
(
)
.
Tsin
Tcosе),T,m(sin
),T,m(cos
),T,m(AA
1
),T,m(K
Tm
дм
дм
дм
п
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
ω
ω−ωϕϕ
ωϕϕ×
×
ω
=ω
ω−
μ
μ
μ
(6. 21)
Переходя к частным случаям ПИ- алгоритма регулирования, получим:
И-алгоритм:
,
),T,m(AA
еTcosе21
T
1
),T,m(K
идм
Tm2
и
Tm
ии
ии
ω
+ω−
=ω
μ
ωω
(6. 22)
где - частота, при которой выполняется условие:
и
ω
.
Tsinе
Tcosе1
arctg
2
),T,m(
и
T
и
m
и
T
и
m
пдм
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω
ω−
+
π
=ωϕϕ
ω
ω
μ
(6. 23)
П-алгоритм:
,
),T,m(AA
1
),T,m(K
пдм
ип
ω
=ω
μ
(6. 24)
где - частота, при которой выполняется условие:
п
ω
. (6. 25)
π
=
ω
ϕ
ϕ
μ
),T,m(
пдм
33

(2)
Дискретный ПДД -алгоритм регулирования:
Дискретная КЧХ ПДД
(2)
алгоритма регулирования имеет вид:
(
)
⋅
−
+
−
+=ω
ω+ω−ω+ω−
2
2
TjTm
дд
TjTm
дпp
T
е1
K
T
е1
KK)j,T,m(W
(6. 26)
Подставив (6. 4),(6. 6), (6. 7) и (6. 26) в (6. 2) и приравняв к нулю действи-
тельную и мнимую составляющие, получим систему уравнений:
34
(
)
(
)
(
)
;01T2sinеTsinе2
T
K
Tsinе
T
K
),T,m(JJ
T2cosеTcosе21
T
K
Tcosе1
T
K
K
),T,m(RR
Tm2Tm
2
дд
Tm
д
дм
Tm2Tm
2
дд
Tm
д
п
дм
=+
⎥
⎦
⎤
⎢
⎣
⎡
ω−ω+ωω−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω+ω−+ω−+×
×
ω
ωωω
μ
ωωω
μ
()()
()
.0T2sinеTsinе2
T
K
Tsinе
T
K
),T,m(RR
T2cosеTcosе21
T
K
Tcosе1
T
K
K
),T,m(JJ
Tm2Tm
2
дд
Tm
д
дм
Tm2Tm
2
дд
Tm
д
п
дм
=
⎥
⎦
⎤
⎢
⎣
⎡
ω−ω+ωω+
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ω+ω−+ω−+×
×ω
ωωω
μ
ωωω
μ
Решив приведенную систему уравнений относительно К и К
п д
, получим
формулы для границы заданного запаса устойчивости:
(
)
(
)
(
)
(
)
;
),T,m(JJ),T,m(RRTsin
Tcosе),T,m(JJTsin),T,m(RR
Tcos2ее1
T
K
),T,m(K
2
дм
2
дм
Tm
дмдм
TmTm
2
дд
п
ω+ωω
ω−⋅ω+ωω
−
−ω−+=ω
μμ
ω−
μμ
ωω
(6. 27)
(
)
()
),T,m(JJ),T,m(RRTsinе
),T,m(JJТ
Tcosе1
T
K2
),T,m(K
2
дм
2
дм
Tm
дм
Tm
дд
д
ω+ωω
ω⋅
+
+ω−−=ω
μμ
ω
μ
ω
(6. 28)
или через расширенные амплитудно- и фазочастотную характеристики:

(
)
(
)
(
)
,
Tsin),T,m(AA
Tsin),T,m(cosTcosе),T,m(sin
Tcos2ее1
T
K
),T,m(K
дм
дм
Tm
дм
TmTm
2
дд
п
ωω
ωωϕϕ−ω−ωϕϕ
+
+ω−+=ω
μ
μ
ω−
μ
ωω
(6. 29)
)
(
35
.
Tsinе),T,m(AA
),T,m(sin
Tcosе1
T
K2
),T,m(K
Tm
дм
дм
Tm
дд
д
ωω
ω
ϕ
ϕ
−ω−−=ω
ω
μ
μ
ω
(6. 30)
Принимая в выведенных формулах m=0, получим выражения для опреде-
ления области устойчивости, к которой можно применить метод введения запа-
са устойчивости посредством пересчета границы этой области; можно рассчи-
тать множество областей устойчивости для определения общей подобласти;
можно учесть информацию о доверительном коридоре на оценку КЧХ объекта
[1].
При Т→0 формулы расчета настроек алгоритмов регулирования сходятся
к известным формулам расчета настроек непрерывных алгоритмов регулирова-
ния [4].
7. Оптимизация настроек цифровых алгоритмов регулирования
Сигнал на выходе непрерывного объекта регулирования ДНСУ является
непрерывным, поэтому для выбора оптимальных настроек цифровых алгорит-
мов регулирования используют те же прямые и косвенные критерии качества
регулирования, как и в непрерывных системах, в частности, — интегральные
критерии для ступенчатых возмущающих воздействий и дисперсию для слу-
чайных воздействий. Специфика расчета этих критериев в ДНСУ заключается в
необходимости перехода от дискретной модели сигнала к непрерывной, что
обеспечивается варьированием параметра с (параметр, характеризующий фик-
ф
тивное запаздывание на выходе ДНСУ, позволяющее провести исследование
поведения выходного сигнала системы между моментами прерывания модуля-
тора) модифицированного Z-преобразования.

Таким образом [5],
()
ф
0
1
0
1z
ф
*
1
cdc,zYTdt)t(yI
∫∫
∞
=
==
, (7. 1)
()
ω
⎥
⎦
⎤
⎢
⎣
⎡
ω
π
==
∫∫∫
∞
π
+
π
−
ddcc,jY|
2
T
dt)t(yI
0
T
T
ф
2
ф
*
1
0
2
2
2
, (7. 2)
()
.ddcc,jG
2
T
D
T
T
2
ф
2
1
0
ф
*
y
2
y
∫∫
π
+
π
−
ω
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
ω
π
=
(7. 3)
В частности, для дисперсии в моменты прерывания:
()
∫
π
+
π
−
ωω
π
=
T
T
*
y
2
y
djG
2
T
D
, (7. 4)
D
y
– обозначает дисперсию регулируемой величины, осредненную на интервале
Т.
За исключением простейших случаев интегралы по c
ф
от
()
ф
*
y
2
ф
*
1z
ф
*
c,G,)c,j(Y,|)c,z(Y ωω
=
не берутся и заменяются соответствую-
щими суммами. Число членов суммы можно ограничить пятью — десятью.
В одноконтурной системе при возмущении по каналу λ:
()
()
(
)
(
)
() ()
()
()
.c,zWzX
zWzWW1
zWc,zWW
zХc,zY
ф
**
*
р
*
дм
*
рф
*
дм
*
ф
*
λ
μ
μ
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
+
−=
(7. 5)
Для случайного возмущающего воздействия формула, определяющая
дисперсию, имеет вид:
36

()
() ()
{}
() ()
()
ω
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
ω
ω⋅ω+
ω−ωω+ω
×
×
π
=
∫∫
π
+
π
−
μ
μμλ
ddcS
jWjWW1
))c,j(WWjWW(jW1c,jW
2
T
D
T
T
1
0
ф
*
x
2
*
р
*
дм
ф
*
дм
*
дм
*
рф
*
2
y
(7. 6)
или иначе:
()
() ()
()
()
() ()
()
.ddcS
jWjWW1
jW)c,j(WW
Re
T
ddcS
jWjWW1
jW)c,j(WW
2
T
DD
T
T
1
0
ф
*
x
*
р
*
дм
*
рф
*
дм
2
T
T
1
0
ф
*
x
2
*
р
*
дм
*
рф
*
дм
2
xy
ω
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
ω
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ωω+
ωω
π
−
−ω
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
ω
ωω+
ωω
×
×
π
+=
∫∫
∫∫
π
+
π
−
μ
μ
π
+
π
−
μ
μ
(7. 7)
Если речь идет о случайном возмущающем воздействии, приведенном к
выходу ДНСУ, то .
()
1c,jW
ф
*
=ω
λ
Z-преобразование спектральной плотности возмущающего значения оп-
ределяется соотношением [7]:
),0(R)1z(R)z(R)z(S)(S
x
*
x
*
x
jz
*
x
*
x
−−+==ω
ω−=
(7. 8)
где — Z-преобразование корреляционной функции возмущающего
)z(R
*
x
воздействия.
При расчете дисперсии на выходе ДНСУ, содержащей объект регулиро-
вания с транспортным запаздыванием, величину запаздывания необходимо
учесть в выражении Z-преобразования КЧХ объекта.
37

8. Примеры расчета
Пример 1. Передаточная функция объекта регулирования:
,
1pT
eK
)p(W
p
+⋅
⋅
=
μ
⋅
τ
−
μ
μ
(8. 1)
где , , а отношение [7].
1K =
μ
1T =
μ
6T/
=
τ
μ
На объекте установлена одноконтурная АСР с дискретным ПИ-
алгоритмом регулирования.
Произведение КЧХ объекта управления и демодулятора имеет вид:
(
)
()
(
)
()
.Т/1где
,
рр
eK
e1
1pTр
eK
e1
1pT
eK
Р
e1
)p(WW
p
Тp
p
Тp
p
Тp
дм
μ
⋅τ−
μ
−
μ
⋅τ−
μ
−
μ
⋅
τ
−
μ
−
μ
=α
α+
⋅α
−=
=
+⋅
⋅
−=
+⋅
⋅
−
=
(8. 2)
Применив модифицированное Z-преобразование (приложение, №11), по-
лучим:
(
)
,z
ez
e
1z
1
z1K)z(WW
r
T
cT
1
дм
−
α−
α
−
−
μμ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−
−=
(8. 3)
где r — целая часть от деления τ на Т, а
).rT/2(1c
−
−
=
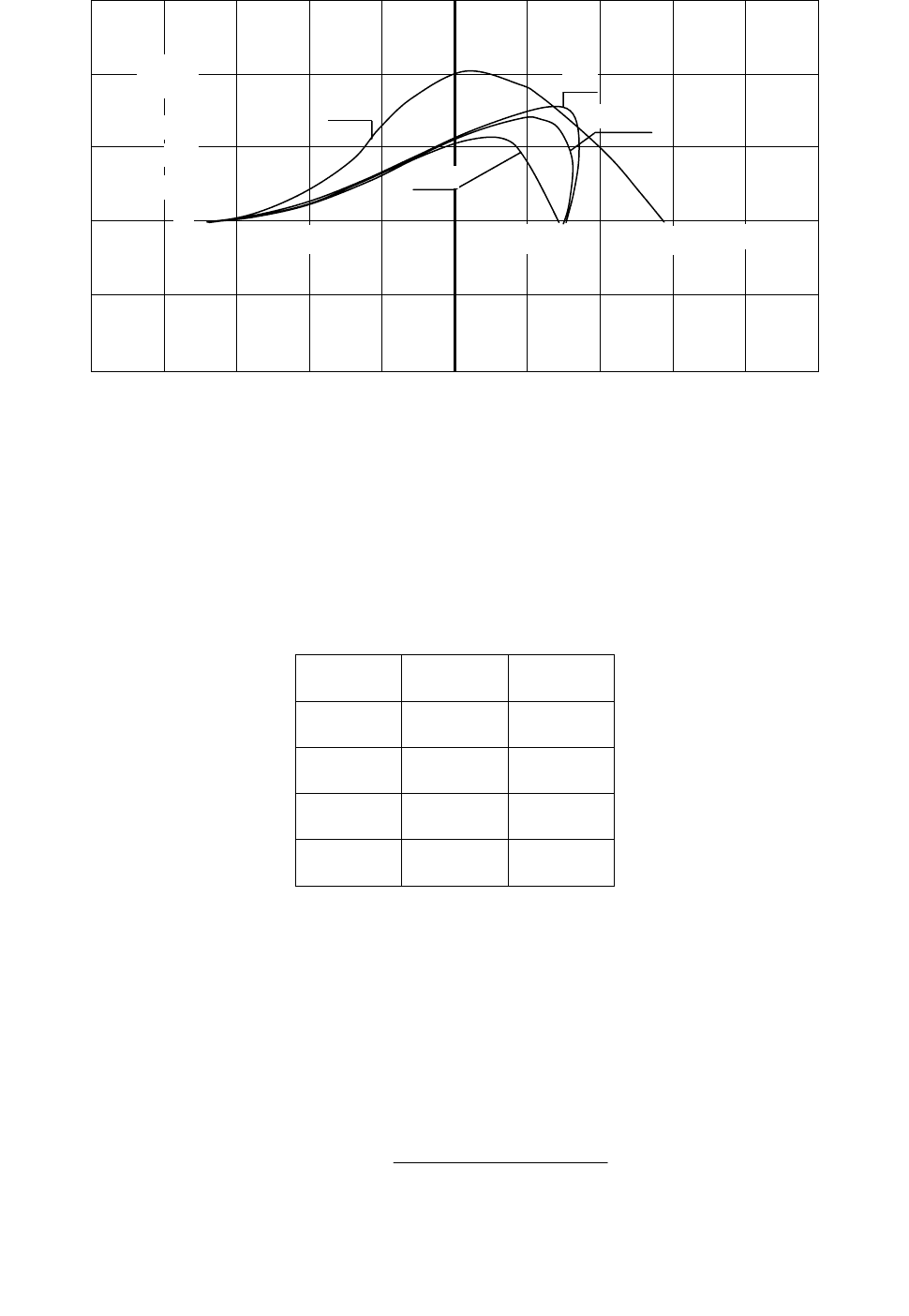
Используя формулы (6.14) и (6.15) для расчета настроек ПИ-алгоритма
регулирования, построим области заданного запаса устойчивости для m=0,366
при шагах дискретизации T=0 (аналоговый ПИ-алгоритм); T=0,14; T=0,7; T=1,7.
Графики областей заданного запаса устойчивости приведены на рис.19.
По линейному интегральному критерию I
38
1
(К →max) находим оптималь-
и
ные настройки дискретного ПИ-алгоритма регулирования для различных шагов
дискретности. Найденные настройки приведены в табл. 1.
39
Рис. 19. Графики линий заданного запаса устойчивости (m=0,366)
одноконтурной ДНСУ с ПИ-алгоритмом регулирования
при различных шагах дискретности Т
Таблица 1
Параметры настроек дискретного ПИ-алгоритма регулирования
Т К
н
К
п
0 1,06 0,329
0,14 0,976 0,3
0,7 0,78 0,0653
1,7 1,45 0,0463
Пример 2. Объект регулирования — стекловаренная печь, канал стабилизации
коэффициента линейного термического расширения. Передаточная функция
объекта регулирования:
()( )
,
1pT1pT
eK
)p(W
21
p
+⋅+⋅
⋅
=
⋅
τ
−
μ
μ
(8. 4)
где =1, T
μ
K
1
=101,2ч, T
2
=26,6ч, а ч2
=
τ
[7].
T=1,7
T=0,7
T=0,14
T=0
1,5
-1
-0,8
-0,6
-0,4
-0,2
0 0,2
0,4
0,6
0,8
1
1,2
К
н
0,9
0,6
0,3
0
К
п
