Griffiths R.B. Consistent Quantum Theory
Подождите немного. Документ загружается.

344 Hardy’s paradox
possibly have affected the outcome of the measurement on particle a,soE
would have occurred in case B
¯
O, just as it did in case B
¯
B.
H3. Since by (25.30) E
¯
F is impossible in this situation, E
¯
E would have
occurred in the case B
¯
O.
H4. Given that
¯
E would have occurred in the case B
¯
O, it would also have oc-
curred with both beam splitters absent, O
¯
O, since, once again, the removal
of a distant beam splitter B at the last instant could not possibly have af-
fected the outcome of a measurement on particle b.
H5. It follows from H1–H4 that if E occurs in the case B
¯
B, then
¯
E would
have occurred, in this particular experiment, if the quantum coin tosses had
resulted in both beam splitters being absent, O
¯
O, rather than present.
H6. Upon interchanging the roles of particles a and b in H1–H4, we conclude
that if
¯
E occurs in the case B
¯
B, then E would have been the case had both
beam splitters been absent, O
¯
O.
H7. Consider a situation in which both E and
¯
E occur in the case B
¯
B; note that
the probability for this is greater than 0, (25.29). Then in the counterfactual
situation in which O
¯
O was the case rather than B
¯
B, we can conclude using
H5 that
¯
E, and using H6 that E, would have occurred. That is, the outcome
of the measurements would have been E
¯
E had the quantum coin tosses
resulted in O
¯
O.
H8. But according to (25.32), E
¯
E cannot occur in the case O
¯
O,sowehave
reached a contradiction.
25.5 Analysis of the second paradox
A detailed analysis of H1–H4 is a bit complicated, since both H2 and H4 involve
counterfactuals, and the conclusion, stated in H5, comes from chaining together
two counterfactual arguments. In order not to become lost in intricate details of
how one counterfactual may be combined with another, it is best to focus on the
end result in H5, which can be restated in the following way: If in the actual world
the quantum coin tosses result in B
¯
B and the measurement outcome is E, then in a
counterfactual world in which the coin tosses had resulted in O
¯
O, particle b would
have triggered detector
¯
E.
To support this argument using the scheme of counterfactual reasoning discussed
in Sec. 19.4, we need to specify a single consistent family which contains the events
we are interested in, which are the outcomes of the coin tosses and at least some
of the outcomes of the final measurements, together with some event (or perhaps
events) at a time earlier than when the quantum coins were tossed, which can serve
as a suitable pivot. The framework might contain more than this, but it must contain
at least this much. (Note that the pivot event or events can make reference to both
25.5 Analysis of the second paradox 345
particles, and could be more complicated than simply the product of a projector for
a times a projector for b.) From this point of view, the intermediate steps in the
argument — for example, H2, in which only one of the beam splitters is removed
— can be thought of as a method for finding the final framework and pivot through
a series of intermediate steps. That is, we may be able to find a framework and
pivot which will justify H2, and then modify the framework and choose another
pivot, if necessary, in order to incorporate H3 and H4, so as to arrive at the desired
result in H5.
We shall actually follow a somewhat different procedure: make a guess for a
framework which will support the result in H5, and then check that it works. An
intelligent guess is not difficult, for E in case B
¯
B implies that the b particle was
earlier in the
¯
d arm of its interferometer, (25.13), and when the beam splitter
¯
B is
out of the way, a particle in
¯
d emerges in the ¯e channel, which will result in
¯
E.This
suggests taking a look at the consistent family containing the following histories,
in which the alternatives ¯c and
¯
d occur at t
1
:
%
0
(
¯c (
B
¯
B ( F,
O
¯
O (
¯
F.
¯
d (
B
¯
B ({E, F},
O
¯
O (
¯
E.
(25.33)
The B
¯
O and O
¯
B branches have been omitted from (25.33) in order to save space
and allow us to concentrate on the essential task of finding a counterfactual ar-
gument which leads from B
¯
B to O
¯
O. Including these other branches terminated
by a noncommittal I at t
3
will turn (25.33) into the support of a consistent family
without having any effect on the following argument.
The consistency of (25.33) can be seen in the following way. The events B
¯
B
and O
¯
O are macroscopically distinct, hence orthogonal, and since they remain un-
changed from t
2
to t
3
, we only need to check that the chain operators for the two
histories involving O
¯
O are orthogonal to each other — as is obviously the case,
since the final
¯
E and
¯
F are orthogonal — and the chain operators for the three his-
tories involving B
¯
B are mutually orthogonal. The only conceivable problem arises
because two of the B
¯
B histories terminate with the same projector F. However,
because at earlier times these histories involve orthogonal states ¯c and
¯
d of particle
b,andF has to do with particle a (that is, a measurement on particle a), rather
than b, the chain operators are, indeed, orthogonal. The reader can check this by
working out the chain kets.
One can use (25.33) to support the conclusion of H5 in the following way. The
outcome E in the case B
¯
B occurs in only one history, on the third line in (25.33).
Upon tracing this outcome back to
¯
d as a pivot, and then moving forward in time
346 Hardy’s paradox
on the O
¯
O branch we come to
¯
E as the counterfactual conclusion. Having ob-
tained the result in H5, we do not need to discuss H2, H3, and H4. However, it
is possible to justify these statements as well by adding a B
¯
O branch to (25.33)
with suitable measurement outcomes at t
3
in place of the noncommittal I, and then
adding some more events involving properties of particle a at time t
1
in order to
construct a suitable pivot for the argument in H2. As the details are not essential
for the present discussion, we leave them as a (nontrivial) exercise for anyone who
wishes to explore the argument in more depth.
By symmetry, H6 can be justified by the use of a consistent family (with, once
again, the B
¯
O and O
¯
B branches omitted)
%
0
(
c (
B
¯
B (
¯
F,
O
¯
O ( F,
d (
B
¯
B ({
¯
E,
¯
F},
O
¯
O ( E,
(25.34)
which is (25.33) with the roles of a and b interchanged. However, H7, which
combines the results of H5 and H6, is not valid, because the family (25.33) on
which H5 is based is incompatible with the family (25.34) on which H6 is based.
The problem with combining these two families is that when one introduces the
events E and F at t
3
in the B
¯
B branch of a family which contains c and d at an
earlier time, it is essentially the same thing as introducing e and f to make the
inconsistent family J
1
, (25.25). In the same way, introducing
¯
E and
¯
F in the B
¯
B
branch following an earlier ¯c and
¯
d leads to trouble. Even the very first statement
in H7, that E
¯
E occurs in case B
¯
B with a positive probability, requires the use of
a family which is incompatible with both (25.33) and (25.34)! Thus the road to a
contradiction is blocked by the single-framework rule.
This procedure for blocking the second form of Hardy’s paradox is very similar
to the one used in Sec. 25.3 for blocking the first form of the paradox. Indeed, for
the case B
¯
B we have used essentially the same families; the only difference comes
from the (somewhat arbitrary) decision to word the second form of the paradox in
terms of measurement outcomes, and the first in a way which only makes reference
to particle properties.
The second form of Hardy’s paradox, like the first, cannot be used to justify
some form of quantum nonlocality in the sense of some mysterious long-range
influence of the presence or absence of a beam splitter in the path of one particle
on the behavior of the other particle. Locality was invoked in H2 and H4 (and at
the corresponding points in H6). But H2 and H4, as well as the overall conclusion
in H5, can be supported by using a suitable framework and pivots. (We have only
given the explicit argument for H5.) Thus, while our analysis does not prove that
25.5 Analysis of the second paradox 347
the locality assumptions entering H2 and H4 are correct, it shows that there is no
reason to suspect that there is anything wrong with them. The overall argument,
H1–H8, results in a contradiction. However, the problem lies not in the locality
assumptions in the earlier statements, but rather in the quantum incompatibility
overlooked when writing down the otherwise plausible H7. This incompatibility,
as noted earlier, has to do with the way a single particle is being described, so it
cannot be blamed on anything nonlocal.
Our analysis of H1–H6 was based upon particular frameworks. As there are a
large number of different possible frameworks, one might suppose that an alter-
native choice might be able to support the counterfactual arguments and lead to a
contradiction. There is, however, a relatively straightforward argument to demon-
strate that no single framework, and thus no set of compatible frameworks, could
possibly support the argument in H1–H7. Consider any framework which con-
tains E
¯
E at t
3
both in the case B
¯
B and also in the case O
¯
O. In this framework
both (25.29) and (25.32) are valid: E
¯
E occurs with finite probability in case B
¯
B,
and with zero probability in case O
¯
O. The reason is that even though (25.29)
and (25.32) were obtained using the framework (25.28), it is a general principle
of quantum reasoning, see Sec. 16.3, that the probability assigned to a collection
of events in one framework will be precisely the same in all frameworks which
contain these events and the same initial data (%
0
in the case at hand). But in
any single framework in which E
¯
E occurs with probability 0 in the case O
¯
O it is
clearly impossible to reach the conclusion at the end of a series of counterfactual
arguments that E
¯
E would have occurred with both beam splitters absent had the
outcomes of the quantum coin tosses been different from what actually occurred.
To be more specific, suppose one could find a framework containing a pivot P at
t
1
with the following properties: (i) P must have occurred if B
¯
B was followed by
E
¯
E; (ii) if P occurred and was then followed by O
¯
O, the measurement outcome
would have been E
¯
E. These are the properties which would permit this frame-
work to support the counterfactual argument in H1–H7. But since B
¯
B followed
by E
¯
E has a positive probability, the same must be true of P, and therefore O
¯
O
followed by E
¯
E would also have to occur with a finite probability. (A more de-
tailed analysis shows that Pr(E
¯
E, t
3
| O
¯
O, t
2
) would have to be at least as large
as Pr(E
¯
E, t
3
| B
¯
B, t
2
).) However, since O
¯
O is, in fact, never followed by E
¯
E,a
framework and pivot of this kind does not exist.
The conclusion is that it is impossible to use quantum reasoning in a consis-
tent way to arrive at the conclusion H7 starting from the assumption H1. In some
respects the analysis just presented seems too simple: it says, in effect, that if a
counterfactual argument of the form H1–H7 arrives at a contradiction, then this
very fact means there is some way in which this argument violates the rules of
quantum reasoning. Can one dispose of a (purported) paradox in such a summary
348 Hardy’s paradox
fashion? Yes, one can. The rule requiring that quantum reasoning of this type
employ a single framework means that the usual rules of ordinary (classical) rea-
soning and probability theory can be applied as long as one sticks to this particular
framework, and there can be no contradiction. To put the matter in a different way,
if there is some very clever way to produce this paradox using only one framework,
then there will also be a corresponding “classical” paradox, and whatever it is that
is paradoxical will not be unique to quantum theory.
Nonetheless, there is some value in our working out specific aspects of the para-
dox using the explicit families (25.33) and (25.34), for they indicate that the basic
difficulty with the argument in H1–H8 lies in an implicit assumption that the dif-
ferent frameworks are compatible, an assumption which is easy to make because
it is always valid in classical mechanics. Incompatibility rather than some myste-
rious nonlocality is the crucial feature which distinguishes quantum from classical
physics, and ignoring it is what has led to a paradox.
26
Decoherence and the classical limit
26.1 Introduction
Classical mechanics deals with objects which have a precise location and move in
a deterministic way as a function of time. By contrast, quantum mechanics uses
wave functions which always have some finite spatial extent, and the time devel-
opment of a quantum system is (usually) random or stochastic. Nonetheless, most
physicists regard classical mechanics as an approximation to quantum mechanics,
an approximation which works well when the object of interest contains a large
number of atoms. How can it be that classical mechanics emerges as a good ap-
proximation to quantum mechanics in the case of large objects?
Part of the answer to the question lies in the process of decoherence in which
a quantum object or system interacting with a suitable environment (which is also
quantum mechanical) loses certain types of quantum coherence which would be
present in a completely isolated system. Even in classical physics the interaction of
a system with its environment can have significant effects. It can lead to irreversible
processes in which mechanical energy is turned into heat, with a resulting increase
of the total entropy. Think of a ball rolling along a smooth, flat surface. Eventually
it comes to rest as its kinetic energy is changed into heat in the surrounding air
due to viscous effects, or dissipated as vibrational energy inside the ball or in the
material which makes up the surface. (From this perspective the vibrational modes
of the ball form part of its “environment”.) While decoherence is (by definition)
quantum mechanical, and so lacks anyexact analog in classical physics, it is closely
related to irreversible effects.
In this chapter we explore a very simple case, one might even think of it as a toy
model, of a quantum particle interacting with its environment as it passes through
an interferometer, in order to illustrate some of the principles which govern deco-
herence. In the final section there are some remarks on how classical mechanics
emerges as a limiting case of quantum mechanics, and the role which decoherence
349
350 Decoherence and the classical limit
plays in relating classical and quantum physics. The discussion of decoherence
and of the classical limit of quantum mechanics presented here is only intended as
an introduction to a complex subject. The bibliography indicates some sources of
additional material.
26.2 Particle in an interferometer
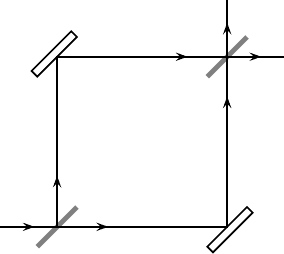
Consider a particle passing through an interferometer, shown schematically in
Fig. 26.1, in which an input beam in channel a is separated by a beam splitter
into two arms c and d, and then passes through a second beam splitter into two
output channels e and f . While this has been drawn as a Mach–Zehnder inter-
ferometer similar to the interferometers considered in earlier chapters, it is best to
think of it as a neutron interferometer or an interferometer for atoms. The prin-
ciples of interference for photons and material particles are the same, but photons
tend to interact with their environment in a different way.
a
c
d
c
d
e
f
B
1
B
2
Fig. 26.1. Particle passing through an interferometer.
Let us suppose that the interferometer is set up so that a particle entering through
channel a always emerges in the f channel due to interference between the waves
in the two arms c and d. As discussed in Ch. 13, this interference disappears if there
is a measurement device in one or both of the arms which determines which arm
the particle passes through. Even in the absence of a measuring device, the particle
may interact with something, say a gas molecule, while traveling through one arm
but not through the other arm. In this way the interference effect will be reduced if
not entirely removed. One refers to this process as decoherence since it removes,
or at least reduces the interference effects resulting from a coherent superposition
of the two wave packets in the two arms. Sometimes one speaks metaphorically of
the environment “measuring” which arm the particle passes through.

26.2 Particle in an interferometer 351
Assume that at the first beam splitter the particle state undergoes a unitary time
development
|a%→(|c+|d)/
√
2, (26.1)
while passage through the arms of the interferometer results in
|c%→|c
, |d%→|d
. (26.2)
Here |a is a wave packet in the input channel at time t
0
, |c and |dare wave pack-
ets emerging from the first beam splitter in the c and d arms of the interferometer at
time t
1
, and |c
and |d
are the corresponding wave packets at time t
2
just before
they reach the second beam splitter. The effect of passing through the second beam
splitter is represented by
|c
%→
|e+|f
/
√
2, |d
%→
−|e+|f
/
√
2, (26.3)
where |e and | f are wave packets in the output channels of the second beam
splitter at time t
3
. The notation is chosen to resemble that used for the toy models
in Sec. 12.1 and Ch. 13.
Nextassume that while inside the interferometer the particle interacts with some-
thing in the environment in a way which results in a unitary transformation of the
form
|c|#%→|c
|#
, |d|#%→|d
|#
, (26.4)
on the Hilbert space A ⊗ E of the particle A and environment E, where |# is the
normalized state of E at time t
1
,and|#
and |#
are normalized states at t
2
.For
example, it might be the case that if the particle passes through the c arm some
molecule is scattered from it resulting in the change from |# to |#
, whereas if
the particle passes through the d arm there is no scattering, and the change in the
environment from |# to |#
is the same as it would have been in the absence of
the particle. The complex number
α =#
|#
=α
+ iα
, (26.5)
with real and imaginary parts α
and α
, plays an important role in the following
discussion. The final particle wave packets |c
and |d
in (26.4) are the same as
in the absence of any interaction with the environment, (26.2). That is, we are
assuming that the scattering process has an insignificant influence upon the center
of mass of the particle itself as it travels through either arm of the interferometer.
This approximation is made in order to simplify the following discussion; one
could, of course, explore a more complicated situation.

352 Decoherence and the classical limit
The complete unitary time evolution of the particle and its environment as the
particle passes through the interferometer is given by
|ψ
0
=|a|#%→
|c+|d
|#/
√
2 %→
|ψ
2
=
|c
|#
+|d
|#
/
√
2 %→
|ψ
3
=
|e
|#
−|#
+|f
|#
+|#
/2,
(26.6)
where we assume that the environment state |# does not change between t
0
and t
1
.
(This is not essential, and one could assume a different state, say |¯#,att
0
, which
develops unitarily into |# at t
1
.) Therefore, in the family with support [ψ
0
] (
I ( I ({[e], [ f ]} the probabilities for the particle emerging in each of the output
channels are given by
Pr(e) =
1
4
#
|−#
|
·
|#
−|#
=
1
4
#
|#
+#
|#
−#
|#
−#
|#
=
1
2
(1 − α
),
Pr( f ) =
1
4
#
|+#
|
·
|#
+|#
=
1
2
(1 + α
).
(26.7)
Because the states entering the inner product in (26.5) are normalized, |α| can-
not be greater than 1. If |#
=|#
, then α
= α = 1 and there is no decoherence:
the interference pattern is the same as in the absence of any interaction with the
environment, and the particle always emerges in f . The interference effect dis-
appears when α
= 0, and the particle emerges with equal probability in e or f .
This could happen even with |α| rather large, for example, α = i. But in such a
case there would still be a substantial coherence between the wave packets in the c
and d arms, and the corresponding interference effect could be detected by shifting
the second beam splitter by a small amount so as to change the difference in path
length between the c and d arms by a quarter wavelength. Hence it seems sensible
to use |α| rather than α
as a measure of coherence between the two arms of the
interferometer, and 1 −|α| as a measure of the amount of decoherence.
26.3 Density matrix
In a situation in which one is interested in what happens to the particle after it
passes through the second beam splitter without reference to the final state of the
environment, it is convenient to use a density matrix ρ
2
for the particle at the inter-
mediate time t
2
in (26.6), just before the particle passes through the second beam
splitter. By taking a partial trace over the environment E in the manner indicated
in Sec. 15.3, one obtains
ρ
2
= Tr
E
|ψ
2
ψ
2
|
=
1
2
|c
c
|+|d
d
|+α|c
d
|+α
∗
|d
c
|
. (26.8)

26.3 Density matrix 353
This has the form
ρ
2
=
1/2 α/2
α
∗
/21/2
(26.9)
when written as a matrix in the basis {|c
, |d
}, with c
|ρ
2
|c
in the upper left
corner. If we think of ρ
2
as a pre-probability, see Sec. 15.2, its diagonal elements
represent the probability that the particle will be in the c or the d arm. Twice the
magnitude of the off-diagonal elements serves as a convenient measure of coher-
ence between the two arms of the interferometer, and thus 1 −|α| is a measure of
the decoherence.
After the particle passes through the second beam splitter, the density matrix is
given by (see Sec. 15.4)
ρ
3
= T
A
(t
3
, t
2
)ρ
2
T
A
(t
2
, t
3
), (26.10)
where T
A
(t
3
, t
2
) is the unitary transformation produced by the second beam splitter,
(26.3), and we assume that during this process there is no further interaction of the
particle with the environment. The result is
ρ
3
=
1
2
(1 − α
)|ee|+(1 + α
)| f f |+iα
|e f |−|f e|
. (26.11)
The diagonal parts of ρ
3
, the coefficients of |ee| and | f f |, are the probabilities
that the particle will emerge in the e or the f channel, and are, of course, identical
with the expressions in (26.7).
Using a density matrix is particularly convenient for discussing a situation in
which the particle interacts with the environment more than once as it passes
through the c or the d arm of the interferometer. The simplest situation to ana-
lyze is one in which each of these interactions is independent of the others, and
they do not alter the wave packet of the particle. In particular, let the environment
consist of a number of separate pieces (e.g., separate molecules) with a Hilbert
space
E = E
1
⊗ E
2
⊗ E
3
⊗···E
n
(26.12)
and an initial state
|#=|#
1
⊗|#
2
⊗|#
3
⊗···|#
n
(26.13)
at time t
1
. The jth interaction results in |#
j
changing to |#
j
if the particle is in the
c arm, or to |#
j
if the particle is in the d arm. Thus the net effect of all of these
interactions as the particle passes through the interferometer is
|c|#=|c|#
1
|#
2
···|#
n
%→|c
|#
=|c
|#
1
|#
2
···|#
n
,
|d|#=|d|#
1
|#
2
···|#
n
%→|d
|#
=|d
|#
1
|#
2
···|#
n
.
(26.14)
