Griffiths R.B. Consistent Quantum Theory

Подождите немного. Документ загружается.

4 Introduction

exclusive histories forms a sample space or family of histories, where each history

is associated with a projector on a history Hilbert space.

The successive events of a history are, in general, not related to one another

through the Schr

odinger equation. However, the Schr

odinger equation, or, equiva-

lently, the time development operators T(t



, t), can be used to assign probabilities

to the different histories belonging to a particular family. For histories involving

only two times, an initial time and a single later time, probabilities can be assigned

using the Born rule, as explained in Ch. 9. However, if three or more times are

involved, the procedure is a bit more complicated, and probabilities can only be

assigned in a consistent way when certain consistency conditions are satisﬁed, as

explained in Ch. 10. When the consistency conditions hold, the corresponding

sample space or event algebra is known as a consistent family of histories, or a

framework. Checking consistency conditions is not a trivial task, but it is made

easier by various rules and other considerations discussed in Ch. 11. Chapters 9,

10, 12, and 13 contain a number of simple examples which illustrate how the proba-

bility assignments in a consistent family lead to physically reasonable results when

one pays attention to the requirement that stochastic time development must be

described using a single consistent family or framework, and results from incom-

patible families, as deﬁned in Sec. 10.4, are not combined.

1.4 Mathematics I. Linear algebra

Several branches of mathematics are important for quantum theory, but of these

the most essential is linear algebra. It is the fundamental mathematical language

of quantum mechanics in much the same way that calculus is the fundamental

mathematical language of classical mechanics. One cannot even deﬁne essential

quantum concepts without referring to the quantum Hilbert space, a complex linear

vector space equipped with an inner product. Hence a good grasp of what quantum

mechanics is all about, not to mention applying it to various physical problems,

requires some familiarity with the properties of Hilbert spaces.

Unfortunately, the wave functions for even such a simple system as a quan-

tum particle in one dimension form an inﬁnite-dimensional Hilbert space, and the

rules for dealing with such spaces with mathematical precision, found in books on

functional analysis, are rather complicated and involve concepts, such as Lebesgue

integrals, which fall outside the mathematical training of the majority of physicists.

Fortunately, one does not have to learn functional analysis in order to understand

the basic principles of quantum theory. The majority of the illustrations used in

Chs. 2–16 are toy models with a ﬁnite-dimensional Hilbert space to which the

usual rules of linear algebra apply without any qualiﬁcation, and for these mod-

els there are no mathematical subtleties to add to the conceptual difﬁculties of

1.5 Mathematics II. Calculus, probability theory 5

quantum theory. To be sure, mathematical simplicity is achieved at a certain cost,

as toy models are even less “realistic” than the already artiﬁcial one-dimensional

models one ﬁnds in textbooks. Nevertheless, they provide many useful insights

into general quantum principles.

For the beneﬁt of readers not already familiar with them, the concepts of linear

algebra in ﬁnite-dimensional spaces which are most essential to quantum theory

are summarized in Ch. 3, though some additional material is presented later: ten-

sor products in Ch. 6 and unitary operators in Sec. 7.2. Dirac notation, in which

elements of the Hilbert space are denoted by |ψ, and their duals by ψ|, the in-

ner product φ|ψ  is linear in the element on the right and antilinear in the one

on the left, and matrix elements of an operator A take the form φ|A|ψ, is used

throughout the book. Dirac notation is widely used and universally understood

among quantum physicists, so any serious student of the subject will ﬁnd learn-

ing it well-worthwhile. Anyone already familiar with linear algebra will have no

trouble picking up the essentials of Dirac notation by glancing through Ch. 3.

It would be much too restrictive and also rather artiﬁcial to exclude from this

book all references to quantum systems with an inﬁnite-dimensional Hilbert space.

As far as possible, quantum principles are stated in a form in which they apply to

inﬁnite- as well as to ﬁnite-dimensional spaces, or at least can be applied to the

former given reasonable qualiﬁcations which mathematically sophisticated readers

can ﬁll in for themselves. Readers not in this category should simply follow the

example of the majority of quantum physicists: go ahead and use the rules you

learned for ﬁnite-dimensional spaces, and if you get into difﬁculty with an inﬁnite-

dimensional problem, go talk to an expert, or consult one of the books indicated in

the bibliography (under the heading of Ch. 3).

1.5 Mathematics II. Calculus, probability theory

It is obvious that calculus plays an essential role in quantum mechanics; e.g., the

inner product on a Hilbert space of wave functions is deﬁned in terms of an inte-

gral, and the time-dependent Schr

odinger equation is a partial differential equation.

Indeed, the problem of constructing explicit solutions as a function of time to the

Schr

odinger equation is one of the things which makes quantum mechanics more

difﬁcult than classical mechanics. For example, describing the motion of a classi-

cal particle in one dimension in the absence of any forces is trivial, while the time

development of a quantum wave packet is not at all simple.

Since this book focuses on conceptual rather than mathematical difﬁculties of

quantum theory, considerable use is made of toy models with a simple discretized

time dependence, as indicated in Sec. 7.4, and employed later in Chs. 9, 12, and

13. To obtain their unitary time development, one only needs to solve a simple

6 Introduction

difference equation, and this can be done in closed form on the back of an envelope.

Because there is no need for approximation methods or numerical solutions, these

toy models can provide a lot of insight into the structure of quantum theory, and

once one sees how to use them, they can be a valuable guide in discerning what are

the really essential elements in the much more complicated mathematical structures

needed in more realistic applications of quantum theory.

Probability theory plays an important role in discussions of the time develop-

ment of quantum systems. However, the more sophisticated parts of this discipline,

those that involve measure theory, are not essential for understanding basic quan-

tum concepts, although they arise in various applications of quantum theory. In

particular, when using toy models the simplest version of probability theory, based

on a ﬁnite discrete sample space, is perfectly adequate. And once the basic strategy

for using probabilities in quantum theory has been understood, there is no partic-

ular difﬁculty — or at least no greater difﬁculty than one encounters in classical

physics — in extending it to probabilities of continuous variables, as in the case of

|ψ(x)|

for a wave function ψ(x).

In order to make this book self-contained, the main concepts of probability the-

ory needed for quantum mechanics are summarized in Ch. 5, where it is shown

how to apply them to a quantum system at a single time. Assigning probabilities

to quantum histories is the subject of Chs. 9 and 10. It is important to note that

the basic concepts of probability theory are the same in quantum mechanics as in

other branches of physics; one does not need a new “quantum probability”. What

distinguishes quantum from classical physics is the issue of choosing a suitable

sample space with its associated event algebra. There are always many different

ways of choosing a quantum sample space, and different sample spaces will often

be incompatible, meaning that results cannot be combined or compared. However,

in any single quantum sample space the ordinary rules for probabilistic reasoning

are valid.

Probabilities in the quantum context are sometimes discussed in terms of a den-

sity matrix, a type of operator deﬁned in Sec. 3.9. Although density matrices are

not really essential for understanding the basic principles of quantum theory, they

occur rather often in applications, and Ch. 15 discusses their physical signiﬁcance

and some of the ways in which they are used.

1.6 Quantum reasoning

The Hilbert space used in quantum mechanics is in certain respects quite dif-

ferent from a classical phase space, and this difference requires that one make

some changes in classical habits of thought when reasoning about a quantum sys-

tem. What is at stake becomes particularly clear when one considers the two-

1.6 Quantum reasoning 7

dimensional Hilbert space of a spin-half particle, Sec. 4.6, for which it is easy to

see that a straightforward use of ideas which work very well for a classical phase

space will lead to contradictions. Thinking carefully about this example is well-

worthwhile, for if one cannot understand the simplest of all quantum systems, one

is not likely to make much progress with more complicated situations. One ap-

proach to the problem is to change the rules of ordinary (classical) logic, and this

was the route taken by Birkhoff and von Neumann when they proposed a special

quantum logic. However, their proposal has not been particularly fruitful for re-

solving the conceptual difﬁculties of quantum theory.

The alternative approach adopted in this book, starting in Sec. 4.6 and sum-

marized in Ch. 16, leaves the ordinary rules of propositional logic unchanged, but

imposes conditions on what constitutes a meaningful quantum description to which

these rules can be applied. In particular, it is never meaningful to combine incom-

patible elements — be they wave functions, sample spaces, or consistent families

— into a single description. This prohibition is embodied in the single-framework

rule stated in Sec. 16.1, but already employed in various examples in earlier chap-

ters.

Because so many mutually incompatible frameworks are available, the strategy

used for describing the stochastic time development of a quantum system is quite

different from that employed in classical mechanics. In the classical case, if one

is given an initial state, it is only necessary to integrate the deterministic equations

of motion in order to obtain a unique result at any later time. By contrast, an

initial quantum state does not single out a particular framework, or sample space

of stochastic histories, much less determine which history in the framework will

actually occur. To understand how frameworks are chosen in the quantum case,

and why, despite the multiplicity of possible frameworks, the theory still leads to

consistent and coherent physical results, it is best to look at speciﬁc examples, of

which a number will be found in Chs. 9, 10, 12, and 13.

Another aspect of incompatibility comes to light when one considers a tensor

product of Hilbert spaces representing the subsystems of a composite system, or

events at different times in the history of a single system. This is the notion of a

contextual or dependent property or event. Chapter 14 is devoted to a systematic

discussion of this topic, which also comes up in several of the quantum paradoxes

considered in Chs. 20–25.

The basic principles of quantum reasoning are summarized in Ch. 16 and shown

to be internally consistent. This chapter also contains a discussion of the intuitive

signiﬁcance of multiple incompatible frameworks, one of the most signiﬁcant ways

in which quantum theory differs from classical physics. If the principles stated in

Ch. 16 seem rather abstract, readers should work through some of the examples

found in earlier or later chapters or, better yet, work out some for themselves.

8 Introduction

1.7 Quantum measurements

A quantum theory of measurements is a necessary part of any consistent way of

understanding quantum theory for a fairly obvious reason. The phenomena which

are speciﬁc to quantum theory, which lack any description in classical physics,

have to do with the behavior of microscopic objects, the sorts of things which

human beings cannot observe directly. Instead we must use carefully constructed

instruments to amplify microscopic effects into macroscopic signals of the sort

we can see with our eyes, or feed into our computers. Unless we understand how

the apparatus works, we cannot interpret its macroscopic output in terms of the

microscopic quantum phenomena we are interested in.

The situation is in some ways analogous to the problem faced by astronomers

who depend upon powerful telescopes in order to study distant galaxies. If they

did not understand how a telescope functions, cosmology would be reduced to

pure speculation. There is, however, an important difference between the “tele-

scope problem” of the astronomer and the “measurement problem” of the quan-

tum physicist. No fundamental concepts from astronomy are needed in order to

understand the operation of a telescope: the principles of optics are, fortunately,

independent of the properties of the object which emits the light. But a piece of

laboratory apparatus capable of amplifying quantum effects, such as a spark cham-

ber, is itself composed of an enormous number of atoms, and nowadays we believe

(and there is certainly no evidence to the contrary) that the behavior of aggregates

of atoms as well as individual atoms is governed by quantum laws. Thus quan-

tum measurements can, at least in principle, be analyzed using quantum theory. If

for some reason such an analysis were impossible, it would indicate that quantum

theory was wrong, or at least seriously defective.

Measurements as parts of gedanken experiments played a very important role

in the early development of quantum theory. In particular, Bohr was able to meet

many of Einstein’s objections to the new theory by pointing out that quantum prin-

ciples had to be applied to the measuring apparatus itself, as well as to the particle

or other microscopic system of interest. A little later the notion of measurement

was incorporated as a fundamental principle in the standard interpretation of quan-

tum mechanics, accepted by the majority of quantum physicists, where it served

as a device for introducing stochastic time development into the theory. As von

Neumann explained it, a system develops unitarily in time, in accordance with

Schr

odinger’s equation, until it interacts with some sort of measuring apparatus,

at which point its wave function undergoes a “collapse” or “reduction” correlated

with the outcome of the measurement.

However, employing measurements as a fundamental principle for interpreting

quantum theory is not very satisfactory. Nowadays quantum mechanics is applied

1.8 Quantum paradoxes 9

to processes taking place at the centers of stars, to the decay of unstable particles

in intergalactic space, and in many other situations which can scarcely be thought

of as involving measurements. In addition, laboratory measurements are often of

a sort in which the measured particle is either destroyed or else its properties are

signiﬁcantly altered by the measuring process, and the von Neumann scheme does

not provide a satisfactory connection between the measurement outcome (e.g., a

pointer position) and the corresponding property of the particle before the mea-

surement took place. Numerous attempts have been made to construct a fully con-

sistent measurement-based interpretation of quantum mechanics, thus far without

success. Instead, this approach leads to a number of conceptual difﬁculties which

constitute what specialists refer to as the “measurement problem.”

In this book all of the fundamental principles of quantum theory are developed,

in Chs. 2–16, without making any reference to measurements, though measure-

ments occur in some of the applications. Measurements are taken up in Chs. 17

and 18, and analyzed using the general principles of quantum mechanics intro-

duced earlier. This includes such topics as how to describe a macroscopic mea-

suring apparatus in quantum terms, the role of thermodynamic irreversibility in the

measurement process, and what happens when two measurements are carried out in

succession. The result is a consistent theory of quantum measurements based upon

fundamental quantum principles, one which is able to reproduce all the results of

the von Neumann approach and to go beyond it; e.g., by showing how the outcome

of a measurement is correlated with some property of the measured system before

the measurement took place.

Wave function collapse or reduction, discussed in Sec. 18.2, is not needed for a

consistent quantum theory of measurement, as its role is taken over by a suitable

use of conditional probabilities. To put the matter in a different way, wave function

collapse is one method for computing conditional probabilities that can be obtained

equally well using other methods. Various conceptual difﬁculties disappear when

one realizes that collapse is something which takes place in the theoretical physi-

cist’s notebook and not in the experimental physicist’s laboratory. In particular,

there is no physical process taking place instantaneously over a long distance, in

conﬂict with relativity theory.

1.8 Quantum paradoxes

A large number of quantum paradoxes have come to light since the modern form

of quantum mechanics was ﬁrst developed in the 1920s. A paradox is something

which is contradictory, or contrary to common sense, but which seems to follow

from accepted principles by ordinary logical rules. That is, it is something which

ought to be true, but seemingly is not true. A scientiﬁc paradox may indicate that

there is something wrong with the underlying scientiﬁc theory, which is quantum

10 Introduction

mechanics in the case of interest to us. But a paradox can also be a prediction

of the theory that, while rather surprising when one ﬁrst hears it, is shown by

further study or deeper analysis to reﬂect some genuine feature of the universe

in which we live. For example, in relativity theory we learn that it is impossible

for a signal to travel faster than the speed of light. This seems paradoxical in

that one can imagine being on a rocket ship traveling at half the speed of light,

and then shining a ﬂashlight in the forwards direction. However, this (apparent)

paradox can be satisfactorily explained by making consistent use of the principles

of relativity theory, in particular those which govern transformations to moving

coordinate systems.

A consistent understanding of quantum mechanics should make it possible to

resolve quantum paradoxes by locating the points where they involve hidden as-

sumptions or ﬂawed reasoning, or by showing how the paradox embodies some

genuine feature of the quantum world which is surprising from the perspective of

classical physics. The formulation of quantum theory found in the ﬁrst sixteen

chapters of this book is employed in Chs. 20–25 to resolve a number of quantum

paradoxes, including delayed choice, Kochen–Specker, EPR, and Hardy’s paradox,

among others. (Schr

odinger’s cat and the double-slit paradox, or at least their toy

counterparts, are taken up earlier in the book, in Secs. 9.6 and 13.1, respectively,

as part of the discussion of basic quantum principles.) Chapter 19 provides a brief

introduction to these paradoxes along with two conceptual tools, quantum coins

and quantum counterfactuals, which are needed for analyzing them.

In addition to demonstrating the overall consistency of quantum theory, there

are at least three other reasons for devoting a substantial amount of space to these

paradoxes. The ﬁrst is that they provide useful and interesting examples of how

to apply the basic principles of quantum mechanics. Second, various quantum

paradoxes have been invoked in support of the claim that quantum theory is in-

trinsically nonlocal in the sense that there are mysterious inﬂuences which can, to

take an example, instantly communicate the choice to carry out one measurement

rather than another at point A to a distant point B, in a manner which contradicts

the basic requirements of relativity theory. A careful analysis of these paradoxes

shows, however, that the apparent contradictions arise from a failure to properly

apply some principle of quantum reasoning in a purely local setting. Nonlocal in-

ﬂuences are generated by logical mistakes, and when the latter are corrected, the

ghosts of nonlocality vanish. Third, these paradoxes have sometimes been used to

argue that the quantum world is not real, but is in some way created by human con-

sciousness, or else that reality is a concept which only applies to the macroscopic

domain immediately accessible to human experience. Resolving the paradoxes, in

the sense of showing them to be in accord with consistent quantum principles, is

thus a prelude to the discussion of quantum reality in Ch. 27.

Wave functions

2.1 Classical and quantum particles

In classical Hamiltonian mechanics the state of a particle at a given instant of

time is given by two vectors: r = (x, y, z) representing its position, and p =

( p

, p

) representing its momentum. One can think of these two vectors to-

gether as determining a point in a six-dimensional phase space. As time increases

the point representing the state of the particle traces out an orbit in the phase space.

To simplify the discussion, consider a particle which moves in only one dimen-

sion, with position x and momentum p. Its phase space is the two-dimensional

x, p plane. If, for example, one is considering a harmonic oscillator with angular

frequency ω, the orbit of a particle of mass m will be an ellipse of the form

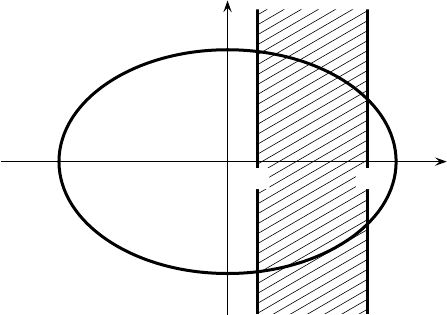
x = A sin(ωt + φ), p = mAω cos(ωt + φ) (2.1)

for some amplitude A and phase φ, as shown in Fig. 2.1.

A quantum particle at a single instant of time is described by a wave function

ψ(r), a complex function of position r. Again in the interests of simplicity we

will consider a quantum particle moving in one dimension, so that its wave func-

tion ψ(x) depends on only a single variable, the position x. Some examples of

real-valued wave functions, which can be sketched as simple graphs, are shown in

Figs. 2.2–2.4. It is important to note that all of the information required to describe

a quantum state is contained in the function ψ(x). Thus this one function is the

quantum analog of the pair of real numbers x and p used to describe a classical

particle at a particular time.

In order to understand the physical signiﬁcance of quantum wave functions, one

needs to know that they belong to a linear vector space H. That is, if ψ(x) and

φ(x) are any two wave functions belonging to H, the linear combination

ω(x) = αψ(x) + βφ(x), (2.2)

where α and β are any two complex numbers, also belongs to H. The space H is

12 Wave functions

Fig. 2.1. Phase space x, p for a particle in one dimension. The ellipse is a possible orbit

for a harmonic oscillator. The cross-hatched region corresponds to x

≤ x ≤ x

equipped with an inner product which assigns to any two wave functions ψ(x) and

φ(x) the complex number

φ|ψ=



+∞

−∞

∗

(x)ψ(x) dx. (2.3)

Here φ

∗

(x) denotes the complex conjugate of the function φ(x). (The notation

used in (2.3) is standard among physicists, and differs in some trivial but annoying

details from that generally employed by mathematicians.)

The inner product φ|ψ is analogous to the dot product

a · b = a

+ a

(2.4)

of two ordinary vectors a and b. One difference is that a dot product is always a

real number, and a · b is the same as b ·a. By contrast, the inner product deﬁned

in (2.3) is in general a complex number, and interchanging ψ(x) with φ(x) yields

the complex conjugate:

ψ|φ=φ|ψ

∗

. (2.5)

Despite this difference, the analogy between a dot product and an inner product is

useful in that it provides an intuitive geometrical picture of the latter.

If φ|ψ=0, which in view of (2.5) is equivalent to ψ|φ=0, the func-

tions ψ(x) and φ(x) are said to be orthogonal to each other. This is analogous to

a · b = 0, which means that a and b are perpendicular to each other. The concept

of orthogonal (“perpendicular”) wave functions, along with certain generalizations

2.2 Physical interpretation of the wave function 13

of this notion, plays an extremely important role in the physical interpretation of

quantum states. The inner product of ψ(x) with itself,

ψ



+∞

−∞

∗

(x)ψ(x) dx, (2.6)

is a positive number whose (positive) square root ψ is called the norm of ψ(x).

The integral must be less than inﬁnity for a wave function to be a member of H.

Thus e

−ax

for a > 0 is a member of H, whereas e

−ax

is not.

A complex linear space H with an inner product is known as a Hilbert space

provided it satisﬁes some additional conditions which are discussed in texts on

functional analysis and mathematical physics, but lie outside the scope of this book

(see the remarks in Sec. 1.4). Because of the condition that the norm as deﬁned

in (2.6) be ﬁnite, the linear space of wave functions is called the Hilbert space of

square-integrable functions, often denoted by L

2.2 Physical interpretation of the wave function

The intuitive signiﬁcance of the pair of numbers x, p used to describe a classical

particle in one dimension at a particular time is relatively clear: the particle is

located at the point x, and its velocity is p/m. The interpretation of a quantum

wave function ψ(x), on the other hand, is much more complicated, and an intuition

for what it means has to be built up by thinking about various examples. We will

begin this process in Sec. 2.3. However, it is convenient at this point to make

some very general observations, comparing and contrasting quantum with classical

descriptions.

Any point x, p in the classical phase space represents a possible state of the

classical particle. In a similar way, almost every wave function in the space H

represents a possible state of a quantum particle. The exception is the state ψ(x)

which is equal to 0 for every value of x, and thus has norm ψ=0. This is

an element of the linear space, and from a mathematical point of view it is a very

signiﬁcant element. Nevertheless, it cannot represent a possible state of a physical

system. All the other members of H represent possible quantum states.

A point in the phase space represents the most precise description one can have

of the state of a classical particle. If one knows both x and p for a particle in one

dimension, that is all there is to know. In the same way, the quantum wave func-

tion ψ(x) represents a complete description of a quantum particle, there is nothing

more that can be said about it. To be sure, a classical “particle” might possess some

sort of internal structure and in such a case the pair x, p,orr, p, would represent

the position of the center of mass and the total momentum, respectively, and one

would need additional variables in order to describe the internal degrees of free-