Griffiths R.B. Consistent Quantum Theory
Подождите немного. Документ загружается.

154 Checking consistency
we can write (11.17) as
α∈S
ˆ
K(Y
α
) =
ˆ
"
0
, (11.22)
and since
ˆ
K(Y) is, like K(Y), a linear function of its argument Y, the argument
leading to
ˆ
K(Y
) = 0, obviously equivalent to K(Y
) = 0, is somewhat more
transparent.
11.6 Initial pure state. Chain kets
If the initial projector of Sec. 11.5 projects onto a pure state,
"
0
= [ψ
0
] =|ψ
0
ψ
0
|, (11.23)
where we will assume that |ψ
0
is normalized, there is an alternative route for cal-
culating weights and checking consistency which involves using chain kets rather
than chain operators. Since it is usually easier to manipulate kets than it is to carry
out the corresponding tasks on operators, using chain kets has advantages in terms
of both speed and simplicity. Suppose that Y
α
in (11.11) has the form given in
(8.30),
Y
α
= [ψ
0
] ( P
α
1
1
( P
α
2
2
(···P
α
f
f
, (11.24)
with projectors at t
1
, t
2
, etc. drawn from decompositions of the identity of the type
(8.25). Then it is easy to see that the corresponding chain operator is of the form
K(Y
α
) =|αψ
0
|, (11.25)
where the chain ket |α is given by the expression
|α=P
α
f
f
T(t
f
, t
f −1
) ···P
α
2
2
T(t
2
, t
1
)P
α
1
1
T(t
1
, t
0
)|ψ
0
. (11.26)
That is, start with |ψ
0
, integrate Schr
¨
odinger’s equation from t
0
to t
1
, and apply
the projector P
α
1
1
to the result in order to obtain
|φ
1
=P
α
1
1
T(t
1
, t
0
)|ψ
0
. (11.27)
Next use |φ
1
as the starting state, integrate Schr
¨
odinger’s equation from t
1
to t
2
,
and apply P
α
2
2
. Continuing in this way will eventually yield |α, where the symbol
α stands for (α
1
,α
2
,...α
f
).
The inner product of two chain operators of the form (11.22) is the same as the
inner product of the corresponding chain kets:
K(Y
α
), K(Y
β
)=Tr
K
†
(Y
α
)K(Y
β
)
= Tr
|ψ
0
α|βψ
0
|
=α|β. (11.28)
11.7 Unitary extensions 155
Consequently, the consistency condition becomes
α|β=0forα = β, (11.29)
while the weight of a history is
W(Y
α
) =α|α. (11.30)
In the special case in which one of the projectors at time t
f
projects onto a pure
state |α
f
, the chain ket will be a complex constant, which could be 0, times |α
f
.
If two or more histories in the sample space have the same final projector onto a
pure state |α
f
, then consistency requires that at most one of these chain kets can
be nonzero.
The analog of the argument in Sec. 11.5 following (11.17) leads to the following
conclusion. Suppose one has a collection S of nonzero chain kets of the form
(11.26) with the property that
α∈S
|α=T(t
f
, t
0
)|ψ
0
. (11.31)
That is, they add up to the state produced by the unitary time evolution of |ψ
0
from t
0
to t
f
. Suppose also that for the collection S the consistency conditions
(11.29) are satisfied. Then one knows that the collection of histories {Y
α
: α ∈ S}
is the support of a consistent family: there is at least one way (and usually there
are many different ways) to add histories of zero weight to the support S in order
to have a sample space satisfying (11.13), with "
0
= [ψ
0
]. Nonetheless, for the
reasons discussed towards the end of Sec. 11.5, it is sometimes a good idea to go
ahead and construct the zero-weight histories explicitly, in order to have a Boolean
algebra of history projectors with certain specific properties, rather than relying on
a general existence proof.
11.7 Unitary extensions
For the following discussion it is convenient to use the Heisenberg representa-
tion introduced in Sec. 11.4, even though the concept of unitary extensions works
equally well for the ordinary (Schr
¨
odinger) representation. Unitary histories were
introduced in Sec. 8.7 and defined by (8.38). An equivalent definition is that the
corresponding Heisenberg operators be identical,
ˆ
F
0
=
ˆ
F
1
=···
ˆ
F
f
, (11.32)
where we have used t
0
as the initial time rather than t
1
as in Sec. 8.7. It is obvi-
ous from (11.9) that the Heisenberg chain operator
ˆ
K for a unitary history is the
projector
ˆ
F
0
.
156 Checking consistency
Next suppose that in place of (11.32) we have
ˆ
F
0
=
ˆ
F
1
=···
ˆ
F
m−1
=
ˆ
F
m
=
ˆ
F
m+1
=···
ˆ
F
f
, (11.33)
where m is some integer in the interval 1 ≤ m ≤ f . We shall call this a “one-jump
history”, because the Heisenberg projectors are not all equal; there is a change, or
“jump” between t
m−1
and t
m
. In a one-jump history there are precisely two types of
Heisenberg projectors, with all the projectors of one type occurring at times which
are earlier than the first occurrence of a projector of the other type. The chain
operator for a history with one jump is
ˆ
K =
ˆ
F
f
ˆ
F
0
. (If, as is usually the case,
ˆ
F
0
and
ˆ
F
f
do not commute,
ˆ
K is not a projector.) Similarly, a history with two jumps
is characterized by
ˆ
F
0
=···
ˆ
F
m−1
=
ˆ
F
m
=···
ˆ
F
m
−1
=
ˆ
F
m
=···
ˆ
F
f
, (11.34)
with m and m
two integers in the range 1 ≤ m < m
≤ f , and its chain operator
is
ˆ
K =
ˆ
F
f
ˆ
F
m
ˆ
F
0
. (It could be the case that
ˆ
F
f
=
ˆ
F
0
.) Histories with three or more
jumps are defined in a similar way.
A unitary extension of a unitary history (11.32) is obtained by adding some ad-
ditional times, which may be earlier than t
0
or between t
0
and t
f
or later than t
f
; the
only restriction is that the new times do not appear in the original list t
0
, t
1
,...t
f
.
At each new time the projector for the event is chosen so that the corresponding
Heisenberg projector is identical to those in the original history, (11.32). Hence, a
unitary extension of a unitary history is itself a unitary history, and its Heisenberg
chain operator is
ˆ
F
0
, the same as for the original history.
A unitary extension of a history with one jump is obtained by including addi-
tional times, and requiring that the corresponding Heisenberg projectors are such
that the new history has one jump. This means that if a new time t
precedes t
m−1
in (11.33), the corresponding Heisenberg projector
ˆ
F
will be
ˆ
F
0
, whereas if it fol-
lows t
m
,
ˆ
F
will be
ˆ
F
m
. If additional times are introduced between t
m−1
and t
m
, then
the Heisenberg projectors corresponding to these times must all be
ˆ
F
0
, or all
ˆ
F
m
,or
if some are
ˆ
F
0
and some are
ˆ
F
m
, then all the times associated with the former must
precede the earliest time associated with the latter. The Heisenberg chain operator
of the extension is the same as for the original history,
ˆ
F
f
ˆ
F
0
.
Unitary extensions of histories with two or more jumps follow the same pattern.
One or more additional times are introduced, and the corresponding Heisenberg
projectors must be such that the number of jumps in the new history is the same
as in the original history. As a consequence, the Heisenberg chain operator is left
unchanged. By using a limiting process it is possible to produce a unitary extension
of a history in which events are defined on a continuous time interval. However, it
is not clear that there is any advantage to doing so.
11.8 Intrinsically inconsistent histories 157
The fact that the Heisenberg chain operator is not altered in forming a unitary
extension means that the weight W of an extended history is the same as that of
the original history. Likewise, if the chain operators for a collection of histories
are mutually orthogonal, the same is true for the chain operators of the unitary
extensions. These results can be used to extend a consistent family of histories to
include additional times without having to recheck the consistency conditions or
recalculate the weights.
There is a slight complication in that while the histories obtained by unitary
extension of the histories in the original sample space form the support of the new
sample space, one needs additional zero-weight histories so that the projectors will
add up to the history identity (or the projector for an initial state). The argument
which follows shows that such zero-weight histories will always exist. Imagine
that some history is being extended in steps, adding one more time at each step.
Suppose that t
has just been added to the set of times, with
ˆ
F
the corresponding
Heisenberg projector. We now define a zero-weight history which has the same
set of times as the newly extended history, and the same projectors at these times,
except that at t
the projector
ˆ
F
is replaced with its complement
ˆ
F
= I −
ˆ
F
. (11.35)
What is
ˆ
K
for the history containing
ˆ
F
? Since the unitary extension had the
same number of jumps as the original history,
ˆ
F
must occur next to an
ˆ
F
in the
product which defines
ˆ
K
, and this means that
ˆ
K
= 0, since
ˆ
F
ˆ
F
= 0. Thus
we have produced a zero-weight history whose history projector when added to
that of the newly extended history yields the projector for the history before the
extension, since
ˆ
F
+
ˆ
F
= I. Consequently, by carrying out unitary extensions
in successive steps, at each step we generate zero-weight histories of the form
needed to produce a final sample space in which all the history projectors add up
to the desired answer. While the procedure just described can always be applied
to generate a sample space, there will usually be other ways to add zero-weight
histories, and since the choice of zero-weight histories can determine what events
occur in the final Boolean algebra, as noted towards the end of Sec. 11.5, one may
prefer to use some alternative to the procedure just described.
11.8 Intrinsically inconsistent histories
A single history is said to be intrinsically inconsistent, or simply inconsistent,if
there is no consistent family which contains it as one of the elements of the Boolean
algebra. The smallest Boolean algebra of histories which contains a history pro-
158 Checking consistency
jector Y consists of 0, Y,
˜
Y =
˘
I − Y, and the history identity
˘
I. Since Y
˜
Y = 0,
K(Y), K(
˜
Y)=0, (11.36)
see (10.21), is a necessary and sufficient condition that Y be intrinsically inconsis-
tent.
If one restricts attention to histories which are product projectors, (8.6), no his-
tory involving just two times can be intrinsically inconsistent, so the simplest pos-
sibility is a three-time history of the form
Y = A ( B ( C. (11.37)
Given Y,define the three histories
Y
= A (
˜
B ( C,
Y
= A ( I (
˜
C,
Y
=
˜
A ( I ( I,
(11.38)
where, as usual,
˜
P stands for I − P. Then it is evident that
Y + Y
+ Y
+ Y
= I ( I ( I =
˘
I, (11.39)
so that
˜
Y = Y
+ Y
+ Y
, (11.40)
and thus
K(
˜
Y) = K(Y
) + K(Y
) + K(Y
). (11.41)
By considering initial and final projectors, Sec. 11.3, it is at once evident that
K(Y
) and K(Y
) are orthogonal to K(Y). Consequently,
K(Y), K(
˜
Y)=K(Y), K(Y
), (11.42)
so that Y is an inconsistent history if the right side of this equation is nonzero.
As an example, consider the histories in (10.35), and let Y = Y
1
. Then Y
= Y
3
,
and (10.37), which was used to show that (10.35) is an inconsistent family, also
shows that Y
1
is intrinsically inconsistent. The same is true of Y
2
, Y
3
,andY
4
. The
same basic strategy can be applied in certain cases which are at first sight more
complicated; e.g., the histories in (13.19).

12
Examples of consistent families
12.1 Toy beam splitter
Beam splitters are employed in optics, in devices such as the Michelson and Mach–
Zehnder interferometers, to split an incoming beam of light into two separate
beams propagating perpendicularly to each other. The analogous situation in a
neutron interferometer is achieved using a single crystal of silicon as a beam split-
ter. The toy beam splitter in Fig. 12.1 can be thought of as a model of either an
optical or a neutron beam splitter. It has two entrance channels (or ports) a and b,
and two exit channels c and d. The sites are labeled by a pair mz, where m is an
integer, and z is one of the four letters a, b, c,ord, indicating the channel in which
the site is located.
The unitary time development operator is T = S
b
, where the action of the oper-
ator S
b
is given by
S
b
|mz=|(m + 1)z, (12.1)
with the exceptions:
S
b
|0a=
+|1c+|1d
/
√
2,
S
b
|0b=
−|1c+|1d
/
√
2.
(12.2)
The physical significance of the states |0a, |1c, etc., is not altered if they are
multiplied by arbitrary phase factors, see Sec. 2.2, and this means that (12.2) is not
the only possible way of representing the action of the beam splitter. One could
equally well replace the states on the right side with
i|1c+|1d
/
√
2,
|1c+i|1d
/
√
2, (12.3)
or make other choices for the phases. There are two other exceptions to (12.1) that
are needed to supply the model with periodic boundary conditions which connect
the c channel back into the a channel and the d channel back into the b channel (or
159
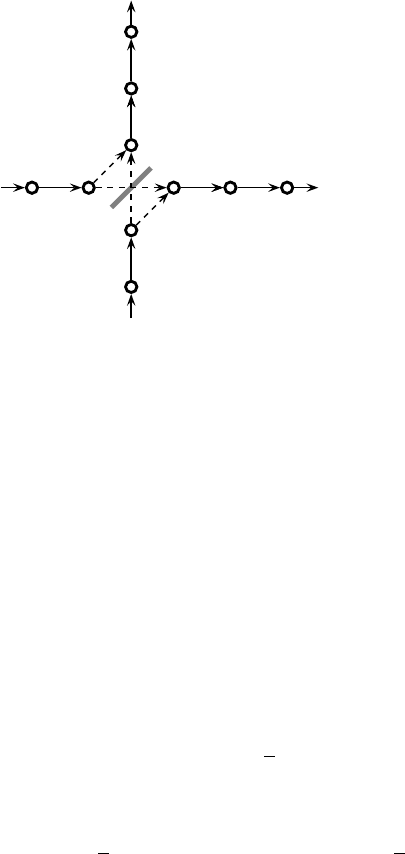
160 Examples of consistent families
−1a 0a
−1b
0b
1c
2c
3c
1d 2d 3d
Fig. 12.1. Toy beam splitter.
c into b and d into a if one prefers). It is not necessary to write down a formula,
since we shall only be interested in short time intervals during which the particle
will not pass across the periodic boundaries and come back to the beam splitter.
That S
b
is unitary follows from the fact that it maps an orthonormal basis of the
Hilbert space, namely the collection of all kets of the form |mz, onto another
orthonormal basis of the same space; see Sec. 7.2.
Suppose that at t = 0 the particle starts off in the state
|ψ
0
=|0a, (12.4)
that is, it is in the a channel and about to enter the beam splitter. Unitary time
development up to a time t > 0 results in
|ψ
t
=S
t
b
|ψ
0
=
|tc+|td
/
√
2 =|t ¯a, (12.5)
where
|m¯a :=
|mc+|md
/
√
2, |m
¯
b :=
−|mc+|md
/
√
2 (12.6)
are the states resulting from unitary time evolution when the particle starts off in
|0a or |0b, respectively.
Let us consider histories involving just two times, with an initial state |ψ
0
=
|0a at t = 0, and a basis at some time t > 0 consisting of the states {|mz}, z = a,
b, c,ord, corresponding to a decomposition of the identity
I =
m,z
[mz]. (12.7)
12.1 Toy beam splitter 161
By treating |ψ
t
as a pre-probability, see Sec. 9.4, one finds that
Pr([mc]
t
) = (1/2)δ
tm
= Pr([md]
t
), (12.8)
while all other probabilities vanish; that is, at time t the particle will be either in the
c output channel at the site tc, or in the d channel at td. Here [mc] is a projector
onto the ray which contains |mc, and the subscript indicates the time at which the
event occurs.
If, on the other hand, one employs a unitary history, Sec. 8.7, in which at time
t the particle is in the state |t ¯a, one cannot say that it is in either the c or the d
channel. The situation is analogous to the case of a spin-half particle with an initial
state |z
+
and trivial dynamics, discussed in Sec. 9.3. In a unitary history with
S
z
=+1/2 at a later time it is not meaningful to ascribe a value to S
x
, whereas by
using a sample space in which S
x
at the later time makes sense, one concludes that
S
x
=+1/2orS
x
=−1/2, each with probability 1/2.
The toy beam splitter is a bit more complicated than a spin-half particle, because
when we say that “the particle is in the c channel”, we are not committed to saying
that it is at a particular site in the c channel. Instead, being in the c channel or
being in the d channel is represented by means of projectors
C =
m
|mcmc|=
m
[mc], D =
m
[md]. (12.9)
Neither of these projectors commutes with a projector [m¯a] corresponding to the
state |m¯a defined in (12.6), so if we use a unitary history, we cannot say that the
particle is in channel c or channel d. Note that whenever it is sensible to speak of
a particle being in channel c or channel d, it cannot possibly be in both channels,
since
CD= 0; (12.10)
that is, these properties are mutually exclusive. A quantum particle can lack a
definite location, as in the state |m ¯a, but, as already pointed out in Sec. 4.5, it
cannot be in two places at the same time.
The fact that the particle is at the site tc with probability 1/2 and at the site td
with probability 1/2 at a time t > 0, (12.8), might suggest that with probability
1/2 the particle is moving out the c channel through a succession of sites 1c,2c,
3c, and so forth, and with probability 1/2 out the d channel through 1d,2d, etc.
But this is not something one can infer by considering histories defined at only two
times, for it would be equally consistent to suppose that the particle hops from 2c
to 3d during the time step from t = 2tot = 3, and from 2d to 3c if it happens
to be in the d channel at t = 2. In order to rule out unphysical possibilities of this
sort we need to consider histories involving more than just two times.
162 Examples of consistent families
Consider a family of histories based upon the initial state [0a] and at each time
t > 0 the decomposition of the identity (12.7), so that the particle has a definite
location. The histories are then of the form, for a set of times t = 0, 1, 2,... f ,
Y = [0a] ( [mz] ( [m
z
] (···[m
z
], (12.11)
with a chain operator of the form K(Y) =|φ0a|, Sec. 11.6, where the chain ket
is
|φ=|m
z
···m
z
|S
b
|mzmz|S
b
|0a. (12.12)
From (12.2) it is obvious that the term mz|S
b
|0a is 0 unless m = 1 and z = c
or d, and given m = 1, it follows from (12.1) that m
z
|S
b
|mz vanishes unless
m
= 2andz
= z. By continuing this argument one sees that |φ, and therefore
K(Y), will vanish for all but two histories, which in the case f = 4 are
Y
c
= [0a] ( [1c] ( [2c] ( [3c] ( [4c],
Y
d
= [0a] ( [1d] ( [2d] ( [3d] ([4d].
(12.13)
The fact that the final projectors [4c] and [4d] in (12.13) are orthogonal to each
other means that the chain operators K(Y
c
) and K(Y
d
) are orthogonal, in accor-
dance with a general principle noted in Sec. 11.3. Since the chain operators of all
the other histories are zero, it follows that Y
c
and Y
d
form the support, as defined in
Sec. 11.2, of a consistent family. It is straightforward to show, either by means of
chain kets as discussed in Sec. 11.6 or by a direct use of W(Y) =K(Y), K(Y),
that
W(Y
c
) = 1/2 = W(Y
d
), (12.14)
and hence, assuming an initial state of [0a] with probability 1, the two histories
Y
c
and Y
d
each have probability 1/2, while all other histories in this family have
probability 0.
The fact that the only histories with finite probability are Y
c
and Y
d
means that
if the particle arrives at the site 1c at t = 1, it continues to move out along the c
channel, and does not hop to the d channel, and if the particle is at 1d at time t = 1,
it moves out along the d channel. Thus by using multiple-time histories one can
eliminate the possibility that the particle hops back and forth between channels c
and d, something which cannot be excluded by considering only two-time histories,
as noted earlier. A formal argument confirming what is rather obviousfrom looking
at (12.13) can be constructed by calculating the probability
Pr(D
t
| [1c]
1
) = Pr(D
t
∧ [1c]
1
)/ Pr([1c]
1
) (12.15)
that the particle will be in the d channel at some time t > 0, given that it was at the
12.1 Toy beam splitter 163
site [1c]att = 1. Here D
t
is a projector on the history space for the particle to be
in channel d at time t. For example, for t = 2,
D
2
= I ( I ( D ( I ( I, (12.16)
and thus
D
2
∧ [1c]
1
= I ( [1c] ( D ( I ( I. (12.17)
This projector gives 0 when applied to either Y
c
or Y
d
, the only two histories with
positive probability, and therefore the numerator on the right side of (12.15) is 0.
Thus if the particle is at 1c at t = 1, it will not be in the d channel at t = 2. The
same argument works equally well for other values of t, and analogous results are
obtained if the particle is initially in the d channel. Thus one has
Pr(D
t
| [1c]
1
) = 0 = Pr(C
t
| [1d]
1
),
Pr(C
t
| [1c]
1
) = 1 = Pr(D
t
| [1d]
1
)
(12.18)
for any t ≥ 1, where C
t
is defined in the same manner as D
t
, with C in place of D.
(Since we are considering a family which is based on the initial state [0a], the
preceding discussion runs into the technical difficulty that C
t
and D
t
do not belong
to the corresponding Boolean algebra of histories when the latter is constructed in
the manner indicated in Sec. 8.5. One can get around this problem by replacing
C
t
and D
t
with the operators C
t
∧[a0]
0
and D
t
∧[a0]
0
, and remembering that the
probabilities in (12.15) and (12.18) always contain the initial state [a0] at t = 0as
an (implicit) condition. Also see the remarks in Sec. 14.4.)
Another family of consistent histories can be constructed in the following way.
At the times t = 1, 2 use, in place of (12.7), a three-projector decomposition of the
identity
I = [t ¯a] + [t
¯
b] + J
t
, (12.19)
where the states |t ¯a, |t
¯
b are defined in (12.6), and
J
t
= I − [t ¯a] − [t
¯
b] = I − [tc] −[td] (12.20)
is a projector for the particle to be someplace other than the two sites tc or td.At
later times t ≥ 3 use the decomposition (12.7). It is easy to show that in the case
f = 4 the two histories
¯
Y
c
= [0a] ( [1¯a] ([2¯a] ( [3c] ( [4c],
¯
Y
d
= [0a] ( [1¯a] ([2¯a] ( [3d] ( [4d],
(12.21)
each with weight 1/2, form the support of the sample space of a consistent family;
all other histories have zero weight.
The histories
¯
Y
c
and
¯
Y
d
in (12.21) have the physical significance that at t =
