Городов Р.В., Губин В.Е., Матвеев А.С. Нетрадиционные и возобновляемые источники энергии
Подождите немного. Документ загружается.

121
котором расстоянии за ветряком, причём полная потеря скорости в два
раза больше потери на ветроколесе.
Через ометаемую поверхность F ветроколеса протекает масса воз-
духа m, количество которой за 1 секунду будет равно:
.mFV
ρ
=
⋅⋅
(7.4.11)
Подставляя значение массы воздуха в выражение кинетической
энергии ветра перед ветроколесом, получим
23
.
22
mV FV
ρ
⋅
⋅⋅
=
(7.4.12)
Взяв отношение секундной работы, воспринятой идеальным вет-
роколесом (7.4.5) к той энергии ветра, которая протекала бы через сече-
ние, равное ометаемой поверхности ветряка (7.4.12), получим идеаль-
ный коэффициент использования энергии ветра
i
ξ
:
1
3
()
.
2
i
PV
V
F
ν
ξ
ρ
⋅
−
=
⋅
⋅
(7.4.13)
Преобразуем это уравнение
11
3
2
()
2.
2
i
PV P V
V
FV V
F
ν
ν
ξ
ρ
ρ
⋅
−−
==⋅⋅
⋅
⋅⋅
⋅
(7.4.14)
Здесь выражение
2
2
P
B
FV
ρ
=⋅
⋅
⋅
(7.4.15)
называют
коэффициентом нагрузки на ометаемую площадь
или
ко-
эффициентом лобового давления
.
Подставив в это уравнение
12 1 1
() ()2PFV FV
ρ
νν ρ ν ν
=⋅⋅ − ⋅ =⋅⋅ − ⋅⋅,
и обозначив
1
e
V
ν
= , после сокращений получим:
11 11
22
()2 ()
244(1).
FV V
B
ee
FV V
ρ
νν νν
ρ
⋅⋅ − ⋅⋅ − ⋅
=⋅ =⋅ =⋅⋅−
⋅⋅
(7.4.16)
Поступая так же с уравнением (7.2.13), для
i
ξ
получим:
2
2
11 1 11
3
3
()2()()
44(1).
2
i
FV V V
ee
V
V
F
ρννν νν
ξ
ρ
⋅⋅ − ⋅⋅⋅ − − ⋅
==⋅=⋅⋅−
⋅
⋅
(7.4.17)
122
Отношение
1
e
V
ν
= называют
коэффициентом торможения
.
Определим значение e, при котором
i
ξ
будет иметь максимальную
величину. Для этого возьмём первую производную и приравняем её ну-
лю, то есть:
223
4(1) 4 8 4 0,
i
dd d
ee ee e
de de de
ξ
⎡⎤⎡ ⎤
=
⋅⋅ − = ⋅−⋅ +⋅ =
⎣⎦⎣ ⎦
(7.4.18)
или
2
416 12 0,
i
d
ee
de
ξ
=
−⋅+⋅= (7.4.19)
откуда
2
3410.ee
⋅
−⋅+= (7.4.20)
Решая это равенство, находим, что
i
ξ
принимает максимальное
значение, когда
1
3
e =
при этом
2
11
4 1 0,593.
33
i
ξ
⎛⎞
=−=
⎜⎟
⎝⎠
(7.4.21)
Из уравнения (7.4.16) находим B – коэффициент нагрузки на оме-
таемую площадь при максимальном
i
ξ
:
11
4 1 0,888.
33
B
⎛⎞
=−=
⎜⎟
⎝⎠
(7.4.22)
Задаваясь коэффициентом торможения
1
e
V
ν
=
в пределах от 0 до 1
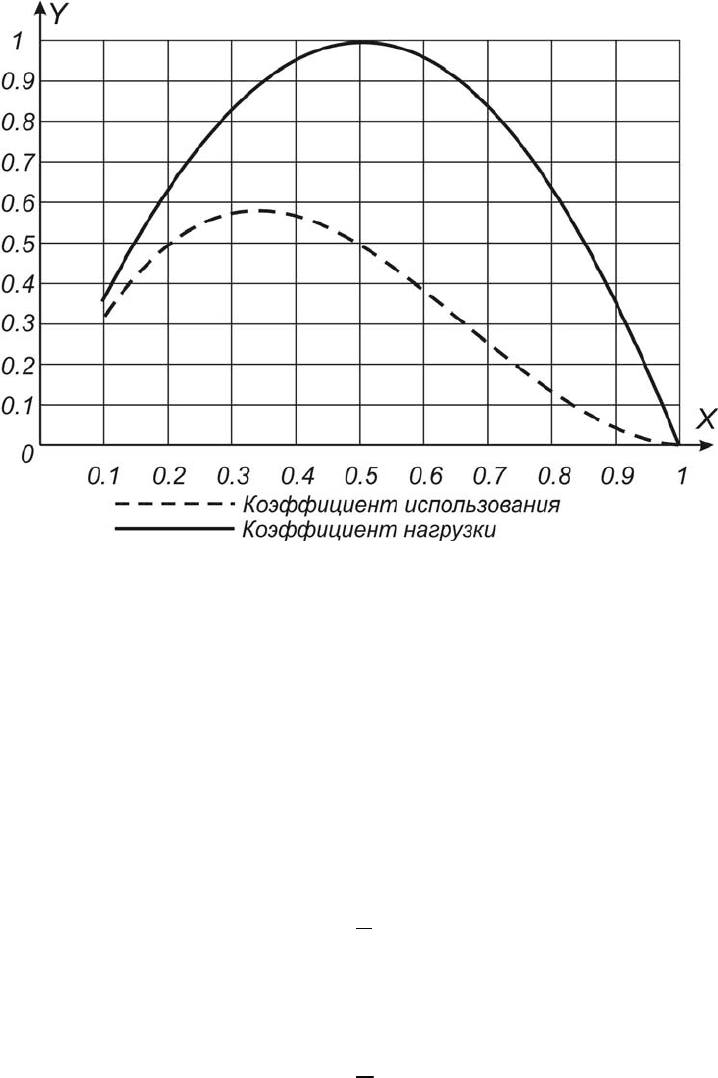
и подсчитывая с помощью уравнений (7.4.13) и (7.4.16), получим сле-
дующие значения коэффициентов
i
ξ
и B (рис. 7.14, табл. 7.4).
Таблица 7.4
Значения коэффициентов использования и нагрузки
в зависимости от коэффициента торможения
1
e
V
ν
=
0,100 0,200 0,333 0,400 0,500 0,600 0,700 0,800 0,900 1,000
i
ξ
0,324 0,512 0,593 0,576 0,500 0,384 0,252 0,128 0,036 0,000
B
0,360 0,640 0,888 0,960 1,000 0,960 0,840 0,640 0,360 0,000
123
Рис. 7.14. Графики зависимости коэффициентов использования и нагрузки
от коэффициента торможения
Таким образом, из классической теории идеального ветряка выте-
кают следующие основные положения:
1. Максимальный коэффициент использования энергии ветра иде-
ального ветроколеса равен
0,593.
i
ξ
=
2. Потеря скорости в плоскости ветроколеса равна одной трети
скорости ветра
1
1
.
3
V
ν
=
⋅
3. Полная потеря скорости ветра за ветроколесом в два раза боль-
ше потери скорости в плоскости ветроколеса
2
2
.
3
V
ν
=
⋅
Таким образом, скорость ветра за ветроколесом в три раза меньше
скорости ветра перед ветроколесом.
4. Коэффициент нагрузки на ометаемую поверхность ветроколеса
равен
0,888.
B
=
124
7.5. Теория реального ветряка
7.5.1. Работа элементарных лопастей ветроколеса.
Первое уравнение связи
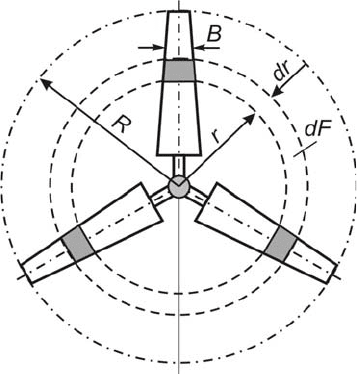
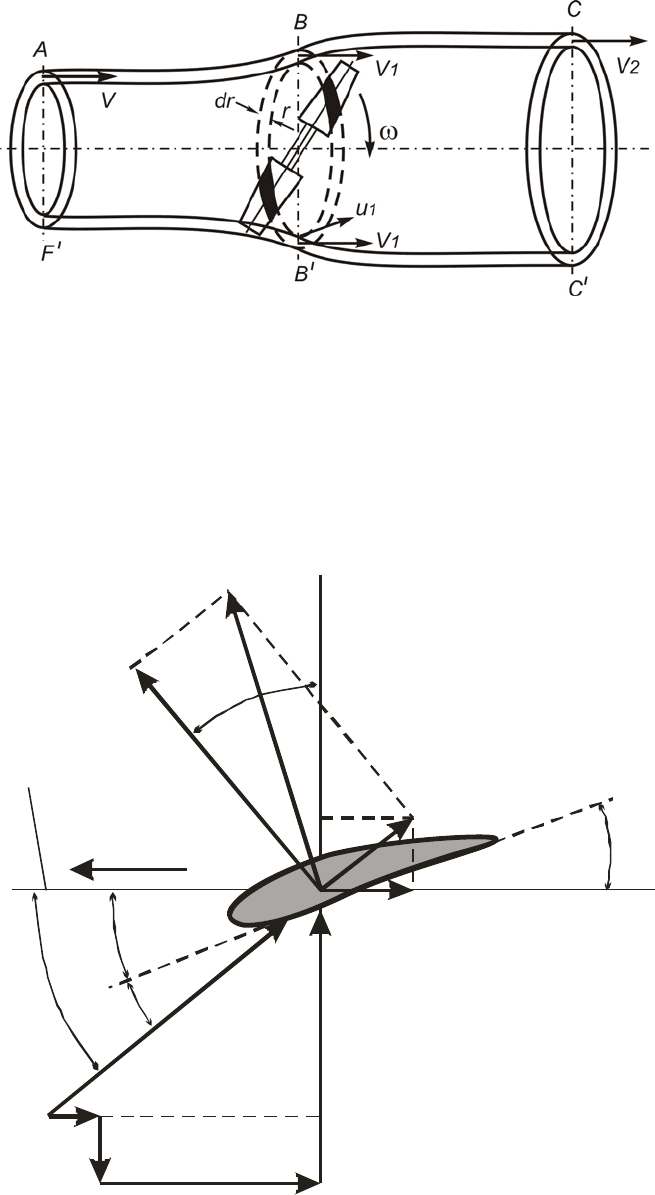
Выделим из лопастей ветроколеса двумя концентрическими ок-
ружностями с радиусами r и r+dr кольцевую поверхность
2dF r dr
π
=⋅⋅⋅ . Это кольцо на крыльях вырежет отрезки длиною dr, ко-
торые называются элементарными лопастями (рис. 7.15). Через все точ-
ки обеих окружностей проведем линии тока, образующие две поверхно-
сти ABC,
A
BC
′′′
бутылеобразной формы (рис. 7.16). Жидкость, заклю-
чённую между этими поверхностями, назовём элементарной кольцевой
струёй.
Сделаем предположение, обычно принимаемое в аналогичных
теориях, что разность давлений по обе стороны ветрового колеса, дей-
ствующая на площадь кольца, получающегося от пересечения ометае-
мой плоскостью элементарной струи, воспринимается элементарными
лопастями.
На основании этого составляем первое уравнение
связи
12
2()(cossin),rdr p p i dY dX
π
ββ
⋅⋅⋅ ⋅ − =⋅ ⋅ + ⋅ (7.5.1.1)
где Y – подъемная сила крыла, направленная перпендикулярно потоку;
X – сила сопротивления крыла (лобовое сопротивление крыла), направ-
ленная по потоку;
β
– угол между плоскостью вращения ветроколеса и
направлением воздушного потока, набегающего на крыло; i – число ло-
пастей ветроколеса.
Рис. 7.15. Выделение элементарных лопастей на ветроколесе
125
Рис. 7.16. Элементарная кольцевая струя
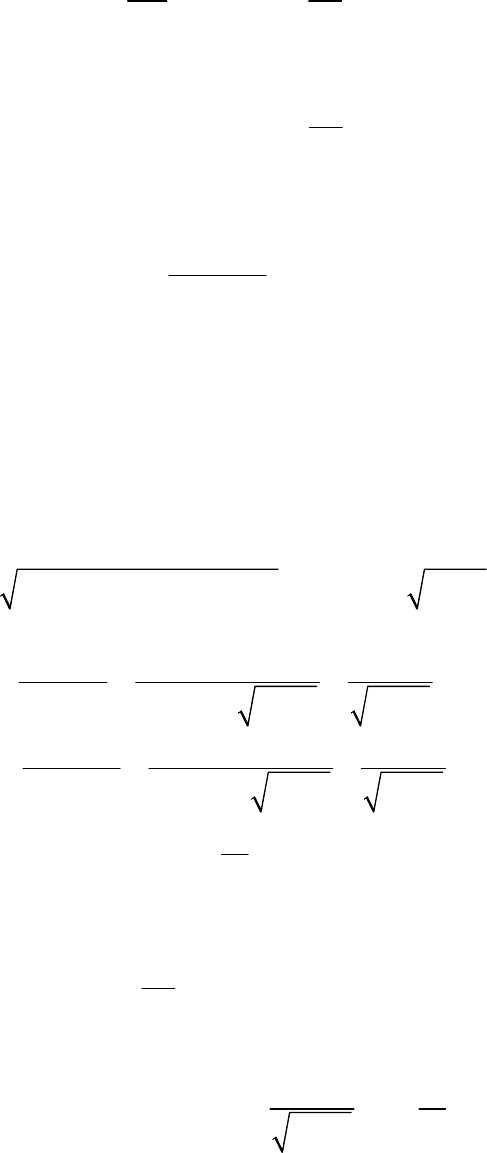
Для определения направления сил, действующих на элементарную
лопасть, изобразим ее сечение на рис. 7.17, где ось Z направлена по оси
ветроколеса и ось x – x в плоскости его вращения; V – направление ско-
рости ветра; W – направление скорости относительного потока, набе-
гающего на элемент лопасти.
XX
Z
Ось ветроколеса
Плоскость
вращения
Направление
вращения
dy
dR
dx
β
β
ϕ
ϕ
w
v
-
ω
r
u
1
v
1
α
Рис. 7.17. План скоростей воздушного потока при набегании его
на элемент лопасти

126
Разложим силу dR, действующую на элементарную лопасть, на
две силы: dX, действующую по потоку, и dY, направленную перпенди-
кулярно потоку. Сила dX вызывает сопротивление элемента крыла; dY
вызывает окружное усилие элемента крыла и называется подъёмной си-
лой.
Вследствие вращения ветроколеса в плоскости x – x воздушный
поток набегает на ветроколесо не со скоростью ветра
V, а с относитель-
ной скоростью W, которая слагается геометрически из скорости ветра V
и окружной скорости
r
ω
⋅ , где
ω
угловая скорость и r – расстояние
элемента лопасти от оси вращения ветроколеса.
Скорость потока, набегающего на элемент лопасти, в относитель-
ном движении будет равна
22
11
()WV ru
ω
=+−⋅−
, (7.5.1.2)
где
11
VV
ν
=−
– скорость ветра в плоскости ветряка.
Скорость u
1
получается как реакция от крутящего момента, разви-
ваемого лопастями. Эта скорость имеет направление, обратное моменту;
её величина берётся как средняя для всей зоны, в которой работают ло-
пасти. В действительности эта скорость перед ветроколесом равна нулю
и непосредственно за ветряком равна u
2
. Так как закон изменения этой
скорости неизвестен, то как первое приближение её принимают равной
2
1
.
2
u
u =
(7.5.1.3)
Силы dY и dX можно выразить как:
2
2
y
dY C b dr W
ρ
=⋅⋅⋅⋅, (7.5.1.4)
2
2
x
dX C b dr W
ρ
=⋅⋅⋅⋅, (7.5.1.5)
где b – ширина элемента лопасти по хорде.
Кроме того, на основании уравнения для лобового давления на
ветряк (по теории идеального ветряка Г.Х. Сабинина) можем написать
12 2
1
P
pp V
F
ρ
ν
−
==⋅⋅ (7.5.1.6)
Подставляя вместо dY и dX и
12
p
p
−
их значения в уравнение
(7.5.1.1), получим
22
2
2cos sin .
22
yx
rdr V i bdrC W bdrC W
ρρ
π
ρν β β
⎛⎞
⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅ ⋅ +⋅⋅⋅⋅ ⋅
⎜⎟
⎝⎠
(7.5.1.7)
127
После сокращения получим
2
2
2cos 1tg
2
x
y
y
WC
rV ibC
C
π
νββ
⎛⎞
⋅⋅⋅⋅ =⋅⋅ ⋅ ⋅ ⋅ + ⋅
⎜⎟
⎜⎟
⎝⎠
; (7.5.1.7а)
или
2
2
4cos 1tg
x
y
y
C
rV ibC W
C
π
νββ
⎛⎞
⋅⋅⋅⋅ =⋅⋅ ⋅ ⋅ ⋅ + ⋅
⎜⎟
⎜⎟
⎝⎠
. (7.5.1.7б)
На основании рис. 7.5.1.3 можно ввести обозначение
1
1
ctg ,
u
ru
z
V
ω
β
ν
⋅
+
=
=
−
(7.5.1.8)
которое называют
числом относительных модулей
.
Из уравнения (7.5.1.8) имеем:
11
-()
u
ru z V
ω
ν
⋅
−=−⋅ −
, (7.5.1.8а)
или
22 2
11
(- ) ( )
u
ru z V
ω
ν
⋅− = ⋅ −
, (7.5.1.8б)
и зная, что
11
VV
ν
=−
, уравнение (7.5.1.2) можем переписать так:
22 2 2
111
() ()()1.
uu
WV zV V z
ννν
=−+⋅−=−⋅+
(7.5.1.9)
Заменим
11
22
1
() () 1
sin
()1 1
uu
VV
W
Vzz
ν
ν
β
ν
−−
== =
−
⋅+ +
, (7.5.1.10)
11
22
1
cos
()1 1
u
uu
ru ru z
W
Vzz
ω
ω
β
ν
⋅+ ⋅+
== =
−
⋅+ +
, (7.5.1.11)
1
tg
u
z
β
=
, (7.5.1.12)
Обратное качество крыла
x
y
C
C
µ
=
, (7.5.1.13)
и подставим их в уравнение (7.5.1.7б):
22
21
2
4()(1)1
1
u
yu
u
u
z
rV ibC V z
z
z
µ
πν ν
⎛⎞
⋅⋅⋅⋅ =⋅⋅ ⋅ − ⋅+ ⋅ ⋅ +
⎜⎟
+
⎝⎠
. (7.5.1.7в)
128
Вводя в это уравнение
1
e
V
ν
=
и заменив
2
ν
его значением из ра-
венства
1
2
1
2
1
V
ν
ν
ν
⋅
=
+
, получим:
2
2
1
8.
(1 ) (1 )
()1
y
uu
e
ibC r
ee
zz
π
µ
⋅⋅ =⋅ ⋅⋅ ⋅
+⋅+
+⋅+
(7.5.1.14)
Это уравнение называется
уравнением связи
, которое связывает
ширину лопасти и коэффициент подъемной силы с деформацией пото-
ка, характеризуемой величиной e.
Взяв сумму проекций сил элемента лопасти на касательную к ок-
ружности, по которой он движется, получим окружное усилие, разви-
ваемое элементарными лопастями
2
(sin cos )
2
yx
dQ i b dr W C C
ρ
β
β
=⋅⋅ ⋅ ⋅ ⋅ ⋅ − ⋅ .
Подставляя сюда значение W,
sin
β
и
cos
β
, и вводя
x
y
CC
µ
=⋅
,
получим:
22
1
2
1
()(1)
2
1
u
uy
u
z
dQ i b dr V z C
z
ρ
µ
ν
−
⋅
=⋅⋅ ⋅ ⋅ − ⋅ + ⋅ ⋅
+
. (7.5.1.15)
Подставляя сюда значение
y
ibC
⋅
⋅
из уравнения (7.5.1.14) и сделав
сокращения, получим
2
1
4
1
u
u
ez
dQ r dr V
ez
µ
πρ
µ
−
⋅
=⋅⋅⋅ ⋅⋅ ⋅ ⋅
++
. (7.5.1.16)
Момент относительно оси ветряка равен
22
1
4
1
u
u
ez
dM dQ r r dr V
ez
µ
πρ
µ
−
⋅
=⋅=⋅⋅⋅⋅⋅ ⋅⋅
++
. (7.5.1.17)
Секундная работа элементарных лопастей
3
1
4.
1
u
u
ez
dT dM r dr V z
ez
µ
ωπ ρ
µ
−
⋅
=⋅=⋅⋅⋅⋅⋅ ⋅⋅ ⋅
++
(7.5.1.18)
Секундная энергия далеко перед ветряком, заключенная в потоке,
площадь сечения которого определяется площадью кольца, сметаемого
элементарными лопастями, равна
3
0
2
2
V
dT r dr
πρ
=⋅⋅⋅ ⋅⋅
. (7.5.1.18а)

129
Поделив секундную работу элементарных лопастей на эту энер-
гию, получим
элементарный коэффициент
использования энергии
ветра
0
41
.
1
u
u
dT e z
z
dT e z
µ
ξ
µ
⋅
−⋅
== ⋅ ⋅
++
(7.5.1.19)
Умножив и разделив выражение (7.5.1.19) на
1 e
−
получим:
11
4.
11
u
u
ezz
e
ez e
µ
ξ
µ
−
−⋅
=⋅⋅ ⋅ ⋅
+
+−
(7.5.1.19а)
Так как выражение
1
4
1
e
e
e
−
⋅⋅
+
представляет
идеальный коэффи-
циент использования энергии ветра
, то можем написать:
1
1
u
ii
u
zz
ze
µ
ξ
ξξη
µ
−
⋅
=⋅ ⋅ =⋅
+−
, (7.5.1.20)
где
1
1
u
u
zz
ze
µ
η
µ
−
⋅
=⋅
+
−
(7.5.1.21)
называют
относительным коэффициентом полезного действия
эле-
ментарного ветряка.
При большом числе модулей можно приблизительно считать
1
u
z
z
e
≅
−
,
и тогда
1
1
u
u
zz
ze
µ
η
µ
−
⋅
=⋅
+
−
. (7.5.1.21а)
Напомним, что
числом модулей
или
быстроходностью
ветро-
двигателя, называют отношение окружной скорости конца лопасти к
скорости ветра:
R
Z
V
ω
⋅
=
.
Число модулей элементов лопастей на радиусе r равно
.
r
z
V
ω
⋅
=
(7.5.1.22)
Число модулей для любого радиуса r ветряка с известной быстро-
ходностью Z может быть выражено так:
r
zZ
R
=
⋅
, (7.5.1.23)
где R – радиус ветроколеса.
130
7.5.2. Второе уравнение связи
Момент относительно оси ветряка аэродинамических сил, дейст-
вующих на элементарные лопасти, равен по величине и противополо-
жен по знаку моменту количества движения, получаемому элементар-
ной струёй, увлечённой ветряным колесом. Здесь предполагается, что в
этом процессе принимает участие и присоединённая масса, так как в
противном случае теорема Гельмгольца о сохранении вихря не
была бы
выполнена.
Второе уравнение связи выводим из рис. 7.17
12 1
(sin cos) ( )2 ,idY dX rdm m ur
β
β
⋅
⋅+⋅ ⋅=+⋅⋅⋅
(7.5.2.1)
но
12
()2dm m r dr V
π
ρ
+=⋅⋅⋅⋅⋅
.
Подставляя указанное уравнение и значения dY и dX из уравнений
(7.5.1.4) и (7.5.1.5) в уравнение (7.5.2.1), получим
2
1
(sin cos ) 2 2 .
2
yx
ibdr C C W r rdr V u r
ρ
ββ πρ
⋅⋅ ⋅ ⋅ − ⋅ ⋅ ⋅ ⋅=⋅ ⋅⋅ ⋅ ⋅ ⋅⋅ ⋅
(7.5.2.1а)
Заменив в этом уравнении
sin
β
и
cos
β
их значениями из урав-
нений (7.5.1.10) и (7.5.1.11) и сделав сокращения, получим:
2
1
22
1
()8.
11
u
yx
uu
z
ib C C W rVu
zz
π
⋅⋅ ⋅ − ⋅ ⋅ =⋅ ⋅⋅ ⋅
++
(7.5.2.1б)
Подставляя сюда (7.5.1.13) и (7.5.1.9), получим:
22
11
2
1
()(1)8 .
1
u
yu
u
z
ibC V z rV u
z
µ
νπ
−⋅
⋅⋅ ⋅ ⋅ − ⋅ + =⋅ ⋅⋅ ⋅
+
(7.5.2.1в)
Из этого равенства находим отношение
1
u
V
, для чего разделим пра-
вую и левую части на
2
8 rV
π
⋅⋅⋅
и заменим отношение
1
V
ν
его значени-
ем e:
22
1
(1 ) (1 ) 1 .
8
y
uu
ibC
u
ezz
Vr
µ
π
⋅⋅
=⋅−⋅−⋅⋅+
⋅⋅
(7.5.2.2)
Подставляя из уравнения (7.5.1.14) значение
8
y
ibC
r
π
⋅
⋅
⋅
⋅
и проведя со-
кращения, получим:
