Гордеев А.В. Операционные системы

Подождите немного. Документ загружается.

252 Глава 8. Проблема тупиков и методы борьбы с нимы

Листинг 8.3 {продолжение)

SEND_ANSWER-( ответ. MB ):

Увы, эти два процесса всегда будут попадать в состояние тупика. Действительно

процесс Пр2, выполняясь первым, сначала будет ожидать сообщения от процесса

Пр1, после чего будет заблокирован при запросе ресурса R, часть которого окажется

уже отданной процессу Пр1. Процесс Пр1, завладев частью ресурса R, будет забло-

кирован ожиданием ответа от Пр2, которого никогда не получит, так как для этого

Пр2 нужно получить ресурс R, находящийся в распоряжении Пр1. Тупика можно

избежать лишь при условии, что на время ожидания ответа от Пр2 процесс Пр1 от-

даст хотя бы одну из единиц ресурса R, которыми он владеет. В данном примере, как

и в предыдущем, причиной тупика являются ошибки программирования.

Пример тупика на ресурсах типа SR

Предположим, что существуют два процесса Пр1 и Пр2, разделяющих два ресурса

типа SR: R1 и R2. Пусть взаимное исключение доступов к этим ресурсам реализует-

ся с помощью семафоров S1 и S2 соответственно. Процессы Пр1 и Пр2 обращаются

к ресурсам так, как показано на рис. 8.3 [17].

Процесс Пр 1 Процесс Пр 2

1: PCS2): (5): PCS1);

2: PCS1): (6): P(S2);

3: VCS1); (7): V(S1);

4: V(S2); (8): V(S2):

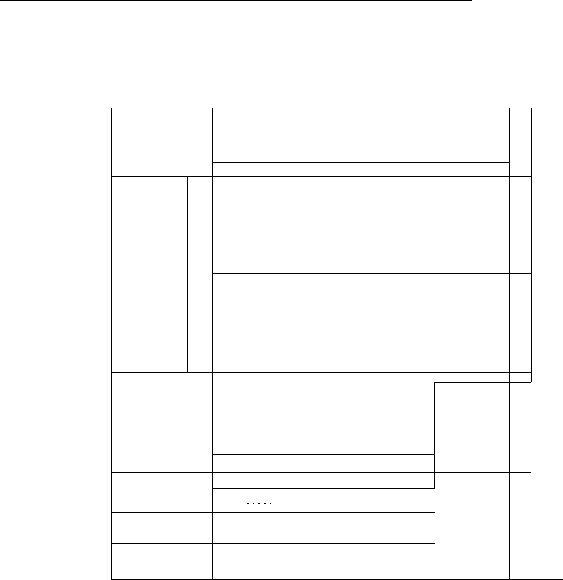
Рис. 8.3. Пример последовательности операторов для двух процессов,

которые могут привести к тупиковой ситуации

Здесь несущественные детали (с точки зрения обращения к ресурсам) опущены.

Считаем, что оба семафора первоначально установлены в единицу. Пространство

возможных состояний приведено на рис. 8.4.

Горизонтальная ось задает выполнение процесса Пр1, вертикальная — процесс

Пр2. Вертикальные линии, пронумерованные от 1 до 4, соответствуют операторам

1-4 процесса Пр1; аналогично горизонтальные линии, пронумерованные от 5 до •

соответствуют операторам 5-8 программы Пр2. Точка на плоскости онределя

состояние вычислений в некоторый момент времени. Так, точка А соответству

ситуации, при которой процесс Пр1 начал исполнение, но не достиг оператора ^

а процесс Пр2 выполнил оператор 6, но не дошел до оператора 7. По мере выпо

рримеры тупиковых ситуаций и причины их возникновения

253

нения точка будет двигаться горизонтально вправо, если исполняется процесс Пр1,

и вертикально вверх, если исполняется процесс Пр2.

Г 7

Пр2

• А

Г ! !

Y I

"1 ""; тнгг-j

! !

—•

^ 5

Пр1

12 3 4

Рис. 8.4. Пространство состояний системы двух параллельных конкурирующих процессов

Интервалы исполнения, во время которых ресурсы R1 и R2 используются каж-

дым процессом, показаны с помощью фигурных скобок. Линии 1-8 делят простран-

ство вычислений на 25 областей, каждая из которых соответствует определенному

состоянию в распределении ресурсов в процессе вычислений. Закрашенные се-

рым цветом состояния являются недостижимыми из-за взаимного исключения

процессов Пр1 и Пр2 при доступе к ресурсам R1 и R2.

Рассмотрим последовательность исполнения 1-2-5-3-6-4-7-8, представленную тра-

екторией Т1. Когда процесс Пр2 запрашивает ресурс R1 (оператор 5), ресурс недо-

ступен (оператор выполнен, семафор закрыт). Поэтому процесс Пр2 заблокиро-

ван в точке В. Как только процесс Пр1 достигнет оператора 3, процесс Пр2

Деблокируется по ресурсу R1. Аналогично в точке С процесс Пр2 будет заблоки-

рован при попытке доступа к ресурсу R2 (оператор 6). Как только процесс Пр1

Достигнет оператора 4, процесс Пр2 деблокируется по ресурсу R2.

Если же, например, выполняется последовательность 1-5-2-6, то процесс ПР1 за-

олокируется в точке X при выполнении оператора 2, а процесс Пр2 заблокируется в

Точке Y при выполнении оператора 6. При этом процесс ПР1 ждет, когда процесс Пр2

выполнит оператор 7, а Пр2 ждет, когда Пр1 выполнит оператор 4. Оба процесса бу-

ДУт находиться в тупике, ни Пр1, ни Пр2 не смогут закончить выполнение. При этом

Вс

е ресурсы, которые получили оба процесса, становятся недоступными для других

254

Глава 8. Проблема тупиков и методы борьбы с ними

процессов, что резко снижает возможности вычислительной системы по их обслужи-

ванию. Отметим одно очень важное обстоятельство: тупик будет неизбежным, если

вычисления зашли в прямоугольник D, являющийся опасным состоянием.

Исследования проблемы тупиков показали, что для возникновения тупиковой

ситуации необходимо одновременное выполнение следующих четырех условий [ 17

54]:

• условия взаимного исключения, при котором процессы осуществляют моно-

польный доступ к ресурсам;

• условия ожидания, при котором процесс, запросивший ресурс, ждет до тех пор,

пока запрос не будет удовлетворен, при этом удерживая ранее полученные ре-

сурсы;

• условия отсутствия перераспределения, при котором ресурсы нельзя отобрать

у процесса, если они ему уже выделены;

Q условия кругового ожидания, при котором существует замкнутая цепь процес-

сов, каждый из которых ждет ресурс, удерживаемый его предшественником в цепи.

Проанализировав содержательный смысл этих четырех условий, легко убедиться,

что все они выполняются в точке Y (см. рис. 8.4).

Формальные модели для изучения

проблемы тупиковых ситуаций

Проблема борьбы с тупиками становится все более актуальной ^сложной по мере

развития и внедрения параллельных вычислительных систем и сетей. При проек-

тировании таких систем разработчики стараются проанализировать возможные

негативные ситуации, используя специальные модели и методы.

К настоящему времени разработано несколько десятков различных моделей, пред-

назначенных для анализа и моделирования систем с параллельными асинхронны-

ми процессами, для которых возможность возникновения тупиковых ситуаций

является очень серьезной проблемой. Изложение и сравнительный анализ этих

моделей может составить большую монографию, поэтому здесь мы лишь кратко

рассмотрим только три из них — сети Петри, модель пространства состояний и уже

упомянутую нами модель Холта.

Сети Петри

Среди многих существующих методов описания и анализа параллельных систем уже

более 35 лет значительное место занимают сетевые модели, восходящие к сетям спе

циального вида, предложенным в 1962 году Карлом Петри для моделирования асин-

хронных информационных потоков в системах преобразования данных [36].

Взаимодействие событий в параллельных асинхронных дискретных системах IIN

ет, как правило, сложную динамическую структуру. Эти взаимодействия опис

ваются проще, если указывать не непосредственные связи между событиями, а

ситуации, при которых данное событие может реализоваться. При этом глооа

формальные модели для изучения проблемы тупиковых ситуаций

255

нЫ

е ситуации в системе формируются с помощью локальных операций, называе-

мых условиями возникновения событий. Определенные сочетания условий допус-

' ают возникновение некоторого события {предусловия события), а реализация

обытия изменяет некоторые условия {постусловия события), то есть события вза-

имодействуют с условиями, а условия — с событиями. Таким образом, предпола-

гается, что для решения задач достаточно представить системы как структуры, об-

разованные из элементов двух типов: событий и условий. Удобное обобщение этого,

предложенное Петри, было развито А. Холтом, который назвал его сетью Петри,

В сетях Петри события и условия представлены абстрактными символами из двух

непересекающихся алфавитов, называемых соответственно множеством переходов

и множеством позиций. Имеется несколько формальных представлений сетей Петри:

О теоретико-множественное представление;

а графово-бихроматический (двудольный ориентированный) граф и, соответ-

ственно, графическое представление;

• матричное представление.

При использовании теоретико-множественного подхода к описанию сети Петри

(поскольку эта модель представляет и структуру, и функционирование системы)

она формально может быть определена как двойка вида N = <S, М

>. Здесь 5 — это

структура сети, которая представляется двудольным ориентированным мульти-

графом S=(V, U), где V— вершины этого графа, U— его дуги. М

— это начальное

состояние сети Петри, которое также называется начальной маркировкой. Сеть

Петри может функционировать и соответственно изменять свое состояние.

В силу того что граф 5 является двудольным, можно перейти к формальному опи-

санию структуры сети Петри в виде тройки:

5=<Р, Т, Y>.

Здесь Р — конечное множество позиций, Р = {р

;

}, i = l,n; Г— конечное множество

переходов, Т = {t

}, j = 1, m; Т U P = V, Т П Р = 0 , то есть Г и Р - это два типа вер-

шин биграфа S\Y — конечное множество дуг, заданное отношениями между вер-

шинами графа 5:

Ye{P-T)\j{T-P). .

Посколькутгвудольный мультиграф 5 является ориентированным, то любой пере-

ход tj, j = \,m, соединяется с позициями p

e P через входные и выходные дуги,

которые задаются через функцию предшествования В : {Р • Т) —> {0,1, 2,...} и функ-

цию следования Е :{Т • Р) —> {0,1, 2,...}, являющиеся отображениями из множества

переходов в комплекты позиций [36] (синонимом термина «комплект» является

онятие мультимножества). Эти функции определяют комплекты позиций

iPii&P, связанных с переходом ^еГ через множество дуг {(р,-/

-)/}>

~ l'(Pi>f;)/

i,j - const} < W, и комплекты позиций {р

}£ Р , связанных с перехо-

дом tj G Г через множестводуг {(t

)

), где 1 < \{{tj,p

)

: j,k = const}| < W. Здесь

~ мультичисло графа 5; Р — пространство комплектов, заданное на множестве Р

Функциями Ей В; {p

)

— v-я дуга, выходящая из позициир, и входящая в пере-

256 Глава 8, Проблема тупиков и методы борьбы с ними

ход t;, (t

)

— v-я дуга, выходящая из перехода t

;

и входящая в позициюр

. Таким

образом, теперь структура S сети Петри Сможет быть представлена как четверка:

<Р,

Т,

В, Е>.

Представим далее множество позиций Р как объединение двух пересекающихся

множеств: P = I\JO; If)O*0. Здесь мы через 1ч О обозначили следующие мно-

жества:

m m

Здесь

I(tj) = {

: B(p

,tj) > 1, i = Гя}, j = tm; 0(£

;

) = {

: £(f

) £ U = u}, .7 = tm;

где (pj, ^.) —дугасвесом да< U

, выходящая из вершины/?, и входящая в вершину ц

(tj<Pk) ~ ДУ

га с

весом w < W, выходящая из вершины t

}

и входящая в вершинур

то есть I(tj) и 0(tj) — комплекты входных и выходных позиций перехода ^соот-

ветственно .

Элементы множества Г обычно представляют собой те возможности (возможные

ситуации, условия), при которых могут быть реализованы интересующие нас про-

цессы (действия).

Начальная маркировка М

(как и текущая маркировка М, которая соответствует

некоторому состоянию сети в текущий момент модельного времени) определяет-

ся одномерной матрицей (вектором), число компонентов которой равно числу по-

зиций сети п, п = \Р\, а значение i-го компонента (1 < i < п ) есть натуральное чис-

ло тп(р

{

), которое определяет количество маркеров (меток) в позиции р;.

=(ш

(р

),тл

(/з

),...,т

(/?„));

М = (m(p

),m(p

),...,m(p„)).

Здесь m

(/j,), m(/?,) e Z ; Z — множество неотрицательных целых чисел. Ее же (мар-

кировку М) можно также представлять как множество или комплект с той разни-

цей, что отсутствие некоторого элемента в множестве будем обозначать специаль-

ным элементом — нулем. В этом случае запись вида М

;

= М

(

_, - I(t) означает

разность множеств и такое изменение маркировки, при котором на соответствую-

щих местах вектора М, будут уменьшенные значения.

Передвижение маркеров по сети осуществляется посредством срабатывания ее

переходов. При срабатывании перехода изменяется маркировка в его входных и вы-

ходных позициях. Получается, что срабатывание возбужденного перехода, являю-

щееся локальным актом, в целом ведет к изменению маркировки сети, то есть к из-

менению ее состояния. Таким образом, если в сети задана начальная маркировка

, при которой хотя бы один переход возбужден, то в сети начинается движение

маркеров, отображающее смену состояний сети. Переход tj может сработать, если

^ррмальные модели для изучения проблемы тупиковых ситуаций

257

р, € Щ) : m(

) > #{

, I(tj)) - w .

Переход, для которого выполняется это условие, называется возбужденным. Здесь

пИ

сь вида #(pi,I(t )) означает число появлений позиций р, во входном комп-

акте перехода t/, оно, естественно, равно весу w соответствующей дуги, если вме-

сто мультиграфа рассматривать взвешенный граф. При срабатывании перехода Ц

маркировка М

изменяется на маркировку М

{

следующим образом:

Иначе говоря:

е Р : Щ(р,) = т

(р,) - #{р„ /(£,)) + #(р„ Щ)) •

Из последнего выражения видно, что количество маркеров, которое переход tj изы-

мает из своих входных позиций, может не равняться количеству маркеров, кото-

рое этот переход помещает в свои выходные позиции, так как совсем не факт, что

число входных дуг перехода равняется числу его выходных дуг.

В графическом представлении сетей (оно наиболее наглядно и легко интер-

претируемо) переходы изображаются вертикальными или горизонтальными

планками (черточками), а позиции — кружками (см. далее). Условия-позиции

и события-переходы связаны отношением непосредственной зависимости (не-

посредственной причинно-следственной связи), которое изображается с помо-

щью направленных дуг, ведущих из позиций в переходы и из переходов в позиции.

Позиции, из которых ведут дуги на данный переход, называются его входными

позициями, а позиции, на которые ведут дуги из данного перехода, — выходны-

ми позициями.

Выполнение условия представляется разметкой соответствующей позиции, а имен-

но помещением числа п в это место или изображением там п маркеров (фишек),

где п — емкость условия (п > 0).

Говорят, что некоторый переход £• для разметки М является живым, если для всех

разметок М\ достижимых из разметки М, существует последовательность сраба-

тывания переходов, приводящая к маркировке М', при которой переход tj может

сработать. Сеть Петри называется живой, если живы все ее переходы; живучая раз-

метка — это разметка, при которой каждый из ее переходов сможет запускаться

бесконечное число раз. Когда достигнута такая разметка, при которой ни один из

переходов не может быть запущен, говорят, что сеть Петри завершилась (достиг-

нута желаемая конечная маркировка) или же зависла (то есть имеет место тупико-

вая ситуация).

Сети Петри очень удобны для описания процессов синхронизации и альтернатив.

Например, семафор может быть представлен входной позицией, связанной с пе-

Колькими взаимоисключающими переходами (критическими секциями). Сети

ет

РИ позволяют моделировать асинхронность и недетерминизм параллельных

езависимых событий, параллелизм конвейерного типа, конфликтные взаимодей-

Твия

Между процессами. Говорят, что два перехода конфликтуют, если они вза-

Но

исключают друг друга, то есть они не могут быть запущены оба одновременно.

258

Глава 8. Проблема тупиков и методы борьбы с ними

Два перехода, готовые к срабатыванию, находятся в конфликте, если они связаны

с общей входной позицией.

В качестве примера рассмотрим рис. 8.5.

О,

ЛЭ5 ОР13

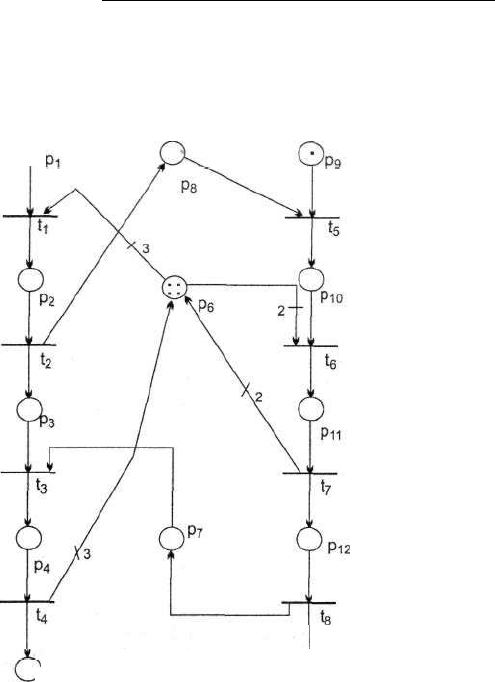
Рис. 8.5. Сеть Петри для системы двух взаимодействующих процессов

Эта сеть соответствует примеру тупиковой ситуации, которая возникает при

взаимодействии процессов Пр1 и Пр2 во время передачи сообщений и потреб-

лении ресурса R каждым из процессов (см. листинг 8.3). Начальная маркиров-

ка для сети, показанной на рис. 8.5, будет равна (1, 0, 0, 0, 0, 4, 0, 0, 1, 0, 0, 0, 0).

Здесь позиция р

означает, что процесс Пр1 получил три единицы ресурса R-

Дуга, соединяющая позицию р

(число маркеров в ней соответствует количе-

ству доступных единиц ресурса R), имеет вес 3, и при срабатывании перехода ц

процесс Пр1 получает затребованные три единицы ресурса. Переход t

пред-

ставляет посылку процессом Пр1 сообщения для Пр2; переход t

— прием этого

сообщения. Появление маркера в позиции р

означает, что процесс Пр2 обра-

ботал сообщение и послал ответ процессу Пр1. Срабатывание перехода t

преД"

ставляет возврат в систему трех единиц ресурса, которыми владел процесс Пр

Рассмотренная сеть не является живой, так как в ней всегда будут мертвы п

реходы t

, L, t

„ t

и t

Примеру тупиковой ситуации, возникающей при работе с ресурсами типа о

(см. рис. 8.3), соответствует сеть Петри, показанная на рис. 8.6.

реальные модели для изучения проблемы тупиковых ситуаций

259

Рис. 8.6. Сеть Петри для тупиковой ситуации на ресурсах типа SR

В этой сети номера переходов соответствуют отмеченным номерам операторов,

которые выполняют процессы Пр1 и Пр2, а позиции р, ир

—

семафорам S1 и S2,

над которыми выполняются операции Р и V. Сеть на рис. 8.6 также не является

живой, хотя для нее и существуют последовательности срабатывания переходов,

не ведущие к тупиковой ситуации.

Сети Петри могут быть использованы для анализа системы на возможность воз-

никновения в ней тупиковых ситуаций. При таком анализе исследуется простран-

ство возможных состояний сети Петри, под которым понимается множество воз-

можных маркировок сети. Для анализа сетей посредством матричных методов

характерно множество проблем, поэтому в основном используется подход, осно-

ванный на построении редуцированного до дерева

графа возможных маркировок

121]. В таком дереве вершины графа — это состояния (маркировки) сети, а ветви

Дерева, помеченные соответствующими переходами сети, — это возможные изме-

нения состояний сети, то есть срабатывания ее переходов.

Модель пространства состояний системы

Приведем еще одну формальную модель (она подробно рассмотрена в работе [54]).

та модель очень проста, однако она позволяет сформулировать, что нам нужно

ать

> чтобы не попасть в тупиковое состояние.

Нал

°Мпим, что деревом в теории графов называют граф, не имеющий циклов.

260

Глава 8. Проблема тупиков и методы борьбы с ними

Пусть состояние операционной системы сводится к состоянию различных ресур-

сов в системе (свободны они или выделены какому-нибудь процессу). Состояние

системы изменяется процессами, когда они запрашивают, приобретают или осво-

бождают ресурсы — это единственно возможные действия (точнее, мы принимаем

во внимание только такие действия). Если процесс не блокирован в данном состо-

янии, он может изменить это состояние на новое. Однако так как в общем случае

невозможно знать априори, какой путь может избрать произвольный процесс в

своей программе (это неразрешимая проблема!), то новое состояние может быть

любым из конечного числа возможных. Следовательно, процессы нами будут трак-

товаться как недетерминированные объекты. Введенные ограничения на извест-

ные понятия приводят нас к нескольким формальным определениям.

О Система есть пара <о, п>, где

а — множество состояний системы { S,, S

, S

,..., S„};

я — множество процессов { Р

(

, Р

, -, Рк }•

Q Процесс Р, есть частичная функция, отображающая состояние системы в непу-

стые подмножества ее же состояний. Это обозначается так:

Р,: G^{Q}.

Если процесс Р

определен на состоянии S, то область значений Р

обозначается

как Pj(S). Если S

e Pj(S

), то мы говорим, что Pj может изменить состояние S

(

, в

состояние S

посредством операции, и используем обозначение S

—-—> S

Наконец, запись S

. —-—> S„, означает, что S

= S

, или S

, —-—> S

для некоторо-

го i, или S

—-—> S

для некоторых i и S

, причем S

—-—> S„..

Другими словами, система может быть переведена посредством п > 0 операций

с помощью m > 0 различных процессов из состояния S

в состояние S

Мы говорим, что процесс заблокирован в данном состоянии, если он не может из-

менить состояние, то есть в этом состоянии процесс не может ни требовать, ни

получать, ни освобождать ресурсы. Поэтому справедливо следующее.

Процесс Р; заблокирован в состоянии S

„ если не существует ни одного состояния

, такого что S

—2—> S

, причем Pj(S

) = 0.

Далее, мы говорим, что процесс Pi находится в тупике в данном состоянии S

, если

он заблокирован в состоянии S

. и если вне зависимости от того, какие операции

(изменения состояний) произойдут в будущем, процесс Pj остается заблокирован-

ным. Поэтому дадим еще одно определение.

Процесс Р; находится в тупике в состоянии S

, если для всех состояний S

, таких

что S

—-—> S

, процесс Р, блокирован в состоянии S

Приведем пример. Определим систему <а, я>:

a = {S

};

тг = {Р

,Р

};

(S,) = {S

}; P

(S,) = {S

};

) = 0; P

) - { S,, S

};

P,(S

) - { S

); P

) = 0;

P,(S.) = { S

}; P

) = 0.

формальные модели для изучения проблемы тупиковых ситуаций

261

Некоторые возможные последовательности изменений для этой системы таковы:

S.-

-> S

; S

; S,

•*s

Последовательность S, —-—> S

может быть реализована, например, следующим

образом: S

(

—^—* S

; S

—

—* S

или же S, —3—> S

; S

—S—> S

Заметим, что процесс Р

находится в тупике как в состоянии S

, так и в состоянии

S • для последнего случая S

—

—> S

или S

—> S

и процесс Р, не оказыва-

ется заблокированным ни в S

, ни в S,.

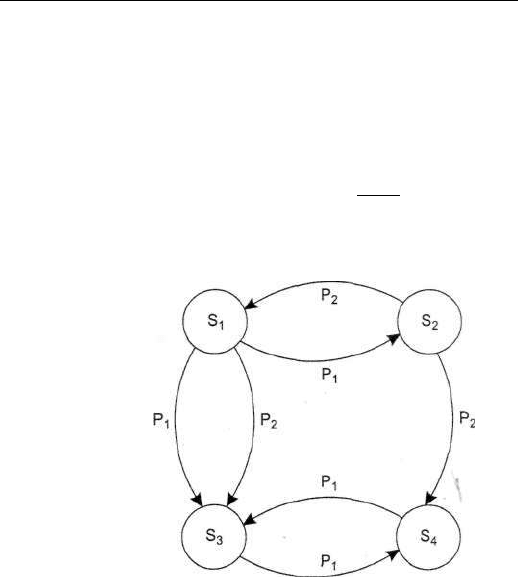
Диаграмма переходов этой системы изображена на рис. 8.7.

Рис. 8.7. Пример системы <<т, п> на четыре состояния

Состояние S называется тупиковым, если существует процесс Р;, находящийся в ту-

пике в состоянии S.

Теперь мы можем сказать, что, по определению, тупик предотвращается при вве-

дении такого ограничения на систему, чтобы каждое ее возможное состояние не

было тупиковым состоянием.

Введем еще одно определение.

Состояние Sj есть безопасное состояние, если для всех S

, таких что S, —-—> S

, S

не является тупиковым состоянием.

Рассмотрим еще один пример системы <о, it>. Граф ее состояний приведен на

Рис. 8.8. Здесь состояния S

и S

являются безопасными; из них система никогда не

сможет попасть в тупиковое состояние. Состояния S, и S

могут привести как к

безопасным состояниям, так и к опасному состоянию S

. Состояния S

и S

явля-

ется тупиковыми.

Наконец, в качестве еще одной простейшей системы вида <а, п> приведем пример

тупика с ресурсами типа SR, уже рассмотренный нами ранее и проиллюстриро-

ванный рис. 8.3. Для этого определим состояния процессов Р

(

и Р

, которые ис-

пользуют ресурсы R

и R

(табл. 8.1).

*Усть состояние системы Sy означает, что процесс Р! находится в состоянии S,,

процесс Р

— в состоянии Sj. Возможные изменения в пространстве состояний