Горбатович Ж.Н., Семенкова А.С. и др. Высшая математика: в 4-х ч., Часть 3
Подождите немного. Документ загружается.

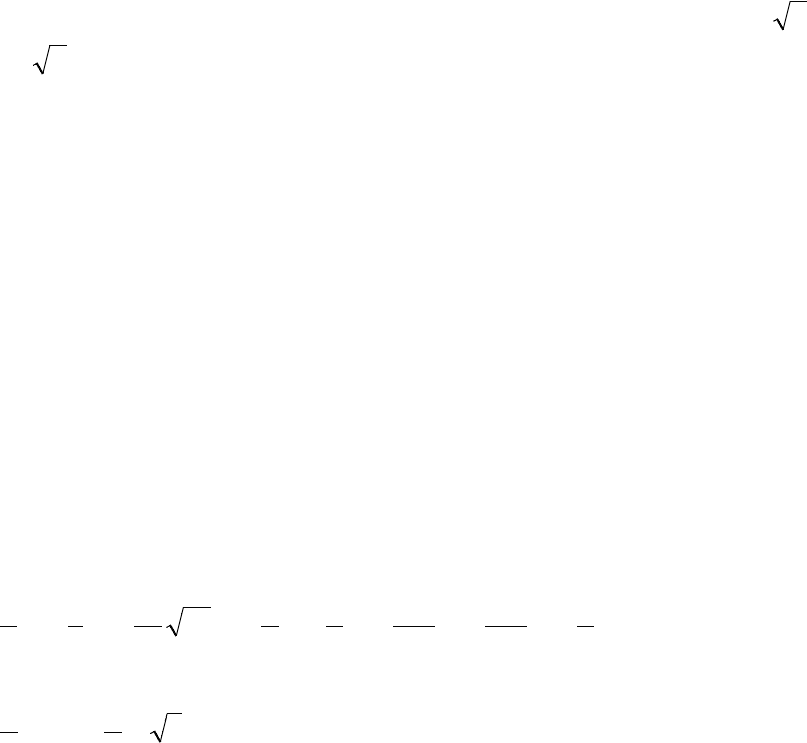
39
10.2.1. Задачи для самостоятельного решения
А
1.
Найти
площадь
фигуры
,
ограниченной
кривой
xy
2
2
=
и
прямой
x
y
=
.
2.
Найти
площадь
фигуры
,
ограниченной
кривой
2
2
xy =
и
прямой
2
=
y
.
3.
Найти
площадь
фигуры
,
ограниченной
кривыми
2510
2
+= xy
и
96
2
+−= xy
.
4.
Найти
площадь
фигуры
,
ограниченной
линиями
xyx
2
22
=+
,
xyx
4
22
=+
,
x
y
=
,
0
=
y
.
5.
Найти
объем
тела
,
ограниченного
поверхностями
xy =
,
xy
2
=
,
4
=
+
z
x
,
0
=
z
.
6.
Найти
объем
тела
,
ограниченного
поверхностями
22
yxz +=
,
2
xy =
,
1
=
y
,
0
=
z
.
7.
Найти
объем
тела
,
ограниченного
поверхностями
0
=
x
,
0
=
y
,
0
=
z
,
22
yxz +=
,
1
=
+
y
x
.
Б
8.
Найти
площадь
фигуры
,
ограниченной
линиями
02
22
=−+ yyx
,
02
22
=−+ xyx
.
9.
Найти
объем
тела
,
ограниченного
поверхностями
22
2
yxz +=
,
3
222
=++ zyx
(
внутри
параболоида
).
10.2.2. Ответы
A
1.
3
2
.
2.
3
8
.
3.
15
3
16
.
4.
2
3
4
3
+π
.
5.
15
128
.
6.
105
88
.
7.
6
1
.
Б
8.
1
2
−
π
.
9.
)536(
3
−
π
.

40
10.3. Тройной интеграл
10.3.1. Основные теоретические сведения
Пусть
в
пространственной
области
3
R
∈
V
определена
и
непрерывна
функция
трех
переменных
)
;
;
(
z
y
x
f
u
=
.
Разобьем
область
V
на
n
произвольных
областей
1
V
,
2
V
,…,
n
V
,
с
объемами
1
V
∆
,
2
V
∆
,…,
n
V
∆
.
В
каждой
области
i
V
(
ni
,1
=
)
выберем
произвольную
точку
);;(
iiii
zyxC
и
составим
интегральную
сумму
=
∆
+
+
∆
+
∆
=
nnn
VCfVCfVCfS
)(...)()(
2211 i
n
i
i
VCf
∑
=
∆
1
)( .
Если
существует
конечный
предел
последовательности
интегральных
сумм
n
S
при
условии
стремления
к
нулю
наибольшего
из
диаметров
i
d
областей
i
V
(
и
∞
→
n
),
не
зависящий
от
способа
разбиения
области
V
на
области
i
V
и
выбора
точек
i
C
,
то
этот
предел
называется
тройным интегралом
от
функции
)
;
;
(
z
y
x
f
u
=
по
области
V
и
обозначается
∫∫∫
V
dVzyxf
);;(
или
∑
∫∫∫
=
→
∞→
∆=
n
i
iiii
d
n
V
Vzyxfdxdydzzyxf
i
1
0max
)(
);;(lim);;( .
10.3.2. Вычисление тройного интеграла
Пусть
функция
трех
переменных
)
;
;
(
z
y
x
f
u
=
определена
и
непрерывна
в
пространственной
области
V
,
которая
ограничена
сверху
поверхностью
);(
2
yxzz
=
,
а
снизу
–
поверхностью
);(
1
yxzz
=
,
где
функции
);(
1
yxz
и
);(
2
yxz
определены
и
непрерывны
в
области
Oxy
D
∈
(
рис
. 10.18).
Тогда
вычисление
тройного
интеграла
сводится
к
последовательному
(
справа
налево
)
вычислению
определенного
интеграла
по
переменной
z
(
переменные
x
и
y
считаются
при
этом
константами
)
и
двойного
интеграла
от
того
,
что
получится
,
по
области
D
.
∫∫ ∫∫∫∫
=
D
yxz
yxzV
dzzyxfdxdydxdydzzyxf
);(
);(
2
1
);;();;(
.
(10.9)
41
Получившийся
двойной
интеграл
можно
вычислять
как
в
декартовой
,
так
и
в
полярной
системе
координат
.
При
вычислении
тройного
интеграла
можно
выбирать
и
другой
порядок
интегрирования
.
Пример 1А.
Вычислить
тройной
интеграл
∫∫∫
V
xydxdydz
,
где
V
–
область
,
ограниченная
поверхностями
22
yxz +=
,
2
=
x
,
2
=
y
и
координатными
плоскостями
.
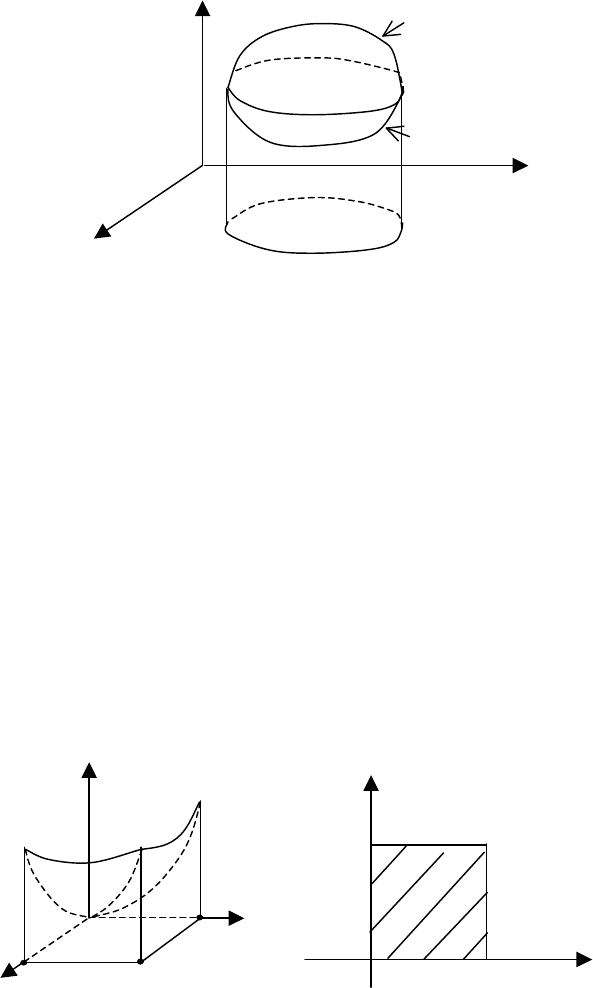
Решение. Область
V
представлена
на
рис
. 10.19.
Поверхность
22
yxz +=
–
параболоид
вращения
,
ограничивает
область
V
сверху
.
Снизу
область
V
ограничена
плоскостью
Oxy
.
Поверхность
2
=
x
–
плоскость
,
параллельная
плоскости
zOy
,
2
=
y
–
плоскость
,
параллельная
плоскости
zOx
.
Проекцией
области
V
на
плоскость
Oxy
будет
квадрат
(
рис
. 10.20) –
область
D
.
По
формуле
(10.9)
имеем
y
z
x
D
0
);(
2
yxzz
=
Рис. 10.18
);(
1
yxzz
=
V
2
D
V
2
0
z
y
x
Рис. 10.19
2
x
y
0
Рис. 10.20
2

42
=
==
+
+
∫∫∫∫∫∫∫∫
dxdyzxyxydzdxdyxydxdydz
yx
D
yx
DV
22
22
0
0
(
)
(
)
(
)
=+=+=+=
∫∫∫∫∫∫
2
0
33
2
0
3322
dyxyyxdxdxdyxyyxdxdyyxxy
DD
( )
16882
2
42
42
2
0
2
4
2
0
3
2
0
2
0
4
2
0
2
3
=+=
+=+=
+
=
∫∫
x
x
dxxxdx
y
x
y
x
.
Пример 2А.
Вычислить
тройной
интеграл
∫∫∫
+
V
dxdydzyx
)( ,
где
V
–
область
,
ограниченная
поверхностями
22
yxz +=
, 4
22
=+ yx
(
0
≥
x
,
0
≥
y
),
0
=
z
.
Решение. Область
V
представлена
на
рис
. 10.21.
Поверхность
22
yxz +=
–
параболоид
вращения
,
который
сверху
ограничивает
область
V
,
снизу
область
V
ограничена
плоскостью
Oxy
(
так
как
0
=
z
).
Поверхность
4
22
=+ yx
–
цилиндрическая
,
направляющей
у
которой
является
окружность
радиуса
2
=
R
.
Так
как
0
≥
x
,
0
≥
y
,
то
рассматриваются
части
поверхностей
в
первом
октанте
.
По
формуле
(10.9)
имеем
=+=+
∫∫∫∫∫∫
+
22
0
)()(
yx
DV
dzyxdxdydxdydzyx
(
)
∫∫
++
D
dxdyyxyx
22
)( .
Так как областью интегрирования
D
является четверть круга
(рис. 10.22), то удобно перейти к полярным координатам:
ϕ
=
cos
r
x
,
ϕ
=
sin
r
y
. Тогда уравнение окружности 4
22
=+ yx .
2
=
r
,
2
0
π
≤ϕ≤ ,
2
0
≤
≤
r
,
dr
rd
dxdy
ϕ
=
.
2
D
V
2
0
z
y
x
Рис. 10.21
2
x
y
0
Рис. 10.22
2

43
(
)
=ϕϕ+ϕ=++
∫∫∫∫
DD
drrdrrrdxdyyxyx
222
)sincos()(
=ϕϕ+ϕ=
∫∫
D
drdr )sin(cos
4
=ϕ+ϕϕ
∫ ∫
π
drrd
2
0
2
0
4
)sin(cos
=ϕ
ϕ+ϕ=ϕϕ+ϕ=
∫∫ ∫
π
π
d
r
drrd
2
0
2
0
5
2
0
2
0
4
5
)sin(cos)sin(cos
=ϕϕ+ϕ=
∫
π
2
0
)sin(cos
5
32
d
5
64
)cos(sin
5
32
2
0
=ϕ−ϕ
π
.
10.3.3. Вычисление объемов с помощью тройного интеграла
Если в тройном интеграле (10.9)
1
)
;
;
(
=
z
y
x
f
в области
V
, то
этот интеграл определяет объем области
V
∫∫∫
=
V
dxdydzV .
(10.10)
Пример 1А.
Найти объем тела, ограниченного поверхностями
22
2 yxz += ,
2
=
z
.
Решение. Данное
тело представлено на рис. 10.23. Тело
ограничено снизу параболоидом вращения
22
2 yxz += , сверху –
плоскостью
2
=
z
, которая пересекает параболоид по окружности
4
22
=+ yx .
Так как область
D
– круг (рис. 10.24), то при вычислении
двойного интеграла переходим к полярным координатам:
ϕ
=
cos
r
x
,
ϕ
=
sin
r
y
, 4
22
=+ yx ,
2
=
r
,
π
≤
ϕ
≤
0
,
2
0
≤
≤
r
,
dr
rd
dxdy
ϕ
=
.
Тогда =
+
−===
∫∫∫∫∫∫∫∫
+
D
yx
DV
dxdy
yx
dzdxdydxdydzV
2
2
22
2
2
22
=ϕ
−=
−ϕ=ϕ
−=
∫∫ ∫∫∫
ππ 2
0
2
0
42
2
0
2
0
32
82
2
2
2
2
2 d
rr
dr
r
rddrrd
r
D
π=ϕ=ϕ−=
π
π
∫
42)24(
2
0
2
0
d
.
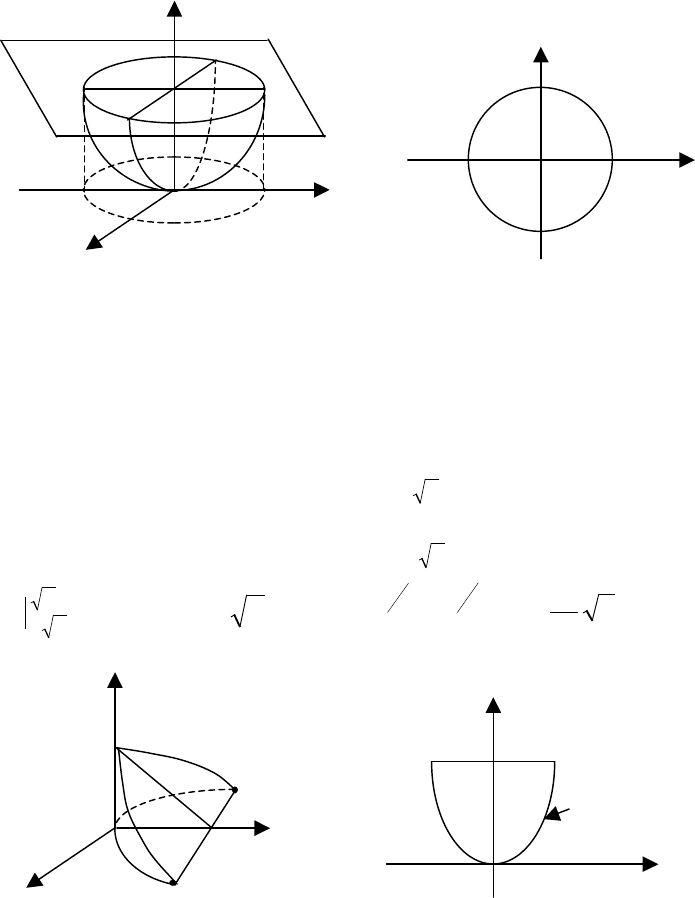
44
Пример 2А.
Найти объем тела, ограниченного поверхностями
0
=
z
,
y
z
−
=
2
,
2
xy = .
Решение. Данное
тело представлено на рис. 10.25, область
D
–
на рис. 10.26. Тогда
=−=−==
∫∫∫∫∫∫ ∫
−
−
y
y
DD
y
dxydydxdyydzdxdyV )2()2(
2
0
2
0
( )
=
−=−=−=
∫∫∫
−
2
0
2
3
2
1
2
0
2
0
222)2(2 dyyydyyydyxy
y
y
2
15
32
.
10.3.4. Задачи для самостоятельного решения
А
1. Расставить пределы в тройном интеграле
∫∫∫
V
dxdydzzyxf );;( по
области, ограниченной поверхностями
а)
0
=
x
,
0
=
y
,
0
=
z
,
1
=
+
+
z
y
x
;
0
2
2
2
D
V
2
0
z
y
x
Рис. 10.23
2
x
y
Рис. 10.24
D
D
2
xy =
0
z
y
x
Рис. 10.25
2
2
A
B
0
2
x
y
2
xy =
Рис. 10.26

45
б) 1
222
=++ zyx ,
0
=
z
(
0
≥
z
).
2. Вычислить а)
∫∫∫
+
−
yx
xy
x
dzdydx
1
0
1
0
; б)
∫∫∫
−+
π
ϕ
22
0
2
0
raa
r
a
dzrdrd .
3. Найти объем тела, ограниченного поверхностями
0
=
x
,
0
=
y
,
0
=
z
,
6
=
+
+
z
y
x
.
4. Найти объем тела, ограниченного поверхностями
22
yxz += и
222
yxz += .
5. Найти объем тела, ограниченного поверхностями
0
=
z
,
2
4 yz −= ,
2
2
x
y = .
10.3.5. Ответы
A
1.
а)
∫∫∫
−−
−
yx
x
dzzyxfdydx
1
0
1
0
1
0
);;( ; б) =
∫∫∫
−−
−
−−
−
22
2
2
1
0
1
1
1
1
);;(
yx
x
x
dzzyxfdydx
∫∫∫
−π
ϕϕϕ
2
1
0
1
0
2
0
);sin;cos(
r
dzzrrfrdrd .
2.
а)
24
7
; б)
4
3
aπ
.
3.
36
.
4.
6
π
.
5.
21
4
12 .

46
Глава 11. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
11.1. Криволинейные интегралы первого рода (КРИ1)
11.1.1. Определение и свойства КРИ1
Пусть в каждой точке гладкой кривой
AB
(или
L
) плоскости
Oxy
задана непрерывная функция двух переменных
)
;
(
y
x
f
z
=
.
Разобьем
AB
на
n
частей точками
0
MA
=
,
1
M ,…, BM
n
=
. На
каждой дуге
ii
MM
1
−
, длина которой
i
l
∆
( ni ,1= ), выберем
произвольно точку );(
iii
yxC .
Составим сумму
=
∆
+
+
∆
+
∆
=
nnn
lCflCflCfS )(...)()(
2211
i
n
i
ii
n
i
ii
lyxflCf ∆=∆=
∑∑
==
11
);()( . Эта сумма называется
интегральной
суммой
первого рода. Пусть
i
ld
∆
=
max – наибольшая из длин дуг
ii
MM
1
−
( ni ,1= ).
Если существует конечный предел последовательности
интегральных сумм
n
S при
0
→
d
, не зависящий ни от способа
разбиения, ни от выбора точек );(
iii
yxC , то этот предел называется
криволинейным интегралом первого рода (КРИ1)
∫
∑
=∆
=
→
AB
n
i
iii
d
dlyxflyxf );();(lim
1
0
.
Если функция
)
;
(
y
x
f
непрерывна на
AB
, то тот предел всегда
существует. Криволинейный интеграл первого рода обладает
свойствами, аналогичными свойствам определенного интеграла
(аддитивность, линейность, оценка модуля, теорема о среднем).
Однако есть отличие
∫∫
=
BAAB
dlyxfdlyxf );();( , т. е. криволинейный
интеграл первого рода
не зависит от направления интегрирования
.
11.1.2. Вычисление криволинейных интегралов первого рода
1. Если кривая
L
задана непрерывно дифференцируемой
функцией
)
(
x
y
ϕ
=
,
[
]
bax ;
∈
, то

47
[ ]
∫∫
ϕ+ϕ=
b
aL
dxxxxfdlyxf
2
)('1))(;();( .
(11.1)
2. Если кривая
L
задана параметрически, т. е. в виде
)
(
t
x
x
=
,
)
(
t
y
y
=
, где
)
(
t
x
,
)
(
t
y
– непрерывно дифференцируемые функции на
промежутке
[
]
β
α
∈
;t , то
[ ] [ ]
∫∫
β
α
+= dttytxtytxfdlyxf
L
22
)(')('))();(();( .
(11.2)
3. Если кривая
L
задана уравнением
)
(
ϕ
=
r
r
,
β
≤
ϕ
≤
α
в
полярных координатах, то
∫∫
β
α
ϕ
ϕ+ϕϕ= drrrrfdlyxf
L
2'2
)()sin;cos();( .
(11.3)
11.1.3. Примеры решения задач
Пример 1А. Вычислить
криволинейный интеграл
∫
L
dl
y
x
, где
L
– дуга параболы xy 2
2
= между точками
)
2
;
2
(
A
и
)
4
;
8
(
B
.
Решение. Кривая
L
– дуга параболы – изображена на рис. 11.1.
Уравнение
L
– xy 2= для
[
]
8;2
∈
x . Используем формулу (11.1) для
вычисления криволинейного интеграла. Найдем
x
y
2
1
'= , тогда
( )
=+⋅+=+=+=
∫∫∫∫
8
2
2
1
8
2
8
2
21
2
1
)12(
2
1
12
22
1
1
2
xdxdxx
x
x
dx
x
x
x
dl
y
x
L
( )
[ ]
551717
6
1
)14()116(
6
1
3
122
4
1
2
3
2
3
8
2
2
3
−=
+−+=
+
=
x
.
Пример 2А. Вычислить
криволинейный интеграл
(
)
∫
+
L
dlyx
32
,
где
L
– контур треугольника
ABO
с вершинами
)
0
;
1
(
A
,
)
1
;
0
(
B
,
)
0
;
0
(
O
.
Решение. Поскольку
(
)
(
)
++=+
∫∫
ABL
dlyxdlyx
3232

48
(
)
(
)
∫∫
++++
OABO
dlyxdlyx
3232
, то остается вычислить криволинейный
интеграл по каждому из отрезков
AB
,
BO
,
OA
(рис. 11.2)
1)
AB
: так как уравнение прямой
AB
имеет вид
x
y
−
=
1
,
[
]
1;0
∈
x , то dxdxdxydl 2)1(1)'(1
22
=−+=+= . Тогда
( )
[ ]
=
−
−=−+=+
∫∫
1
0
43
1
0
3232
4
)1(
3
22)1(
x
x
dxxxdlyx
AB
2
12
7
.
2)
BO
: отрезок
BO
лежит на оси
Oy
, поэтому
0
=
x
,
1
0
≤
≤
y
,
dy
dl
=
и
(
)
4
1
1
0
332
==+
∫∫
dyydlyx
BO
.
3)
OA
:
0
=
y
,
1
0
≤
≤
x
,
dx
dl
=
и
(
)
3
1
1
0
232
==+
∫∫
dxxdlyx
OA
.
Окончательно
(
)
)12(
12
7
3
1
4
1
12
27
32
+=++=+
∫
L
dlyx .
Пример 3А. Вычислить
криволинейный интеграл
∫
+
L
dlyx
22
,
где
L
– окружность
222
Ryx =+ .
Решение. Введем
полярные координаты
ϕ
=
cos
r
x
,
ϕ
=
sin
r
y
.
Тогда, поскольку
222
Ryx =+ , то уравнение окружности примет вид
R
r
=
,
0
'
=
r
, дифференциал дуги ϕ=ϕ=ϕ+= RddRdrrdl
222
)'( .
При этом
[
]
π
∈
ϕ
2;0 . Следовательно, =ϕ⋅=+
∫∫
π
2
0
22
RdRdlyx
L
2
2
R
π .
y
B
A
4
2
8
2
x
Рис. 11.1
0
A
1
y
B
1
x
Рис. 11.2
0
