Горбачев В.В. Концепция современного естествознания
Подождите немного. Документ загружается.


Янко Слава (Библиотека Fort/Da) || http://yanko.lib.ru
Горбачев В. В. Концепции современного естествознания:—М.: ООО «Издательский дом «ОНИКС 21
век»: ООО «Издательство «Мир и Образование», 2003. — 592 с: ил.
131
быть кооперативными, когерентными; 4) должен иметь место неравновесный
термодинамический процесс, причем неравновесность — это такое состояние, когда
приток энергии
214
извне не только «гасит» рост энтропии, но и заставляет энтропию уменьшаться.
Явления, описываемые в рамках понятий бифуркации, самоорганизации и эволюции
структур, относятся не только к физике. Они присущи природе в целом и поэтому могут
быть использованы во всех других науках, которые ее описывают: химии, биологии,
геологии, географии, экологии. Это связано с тем, что методы анализа таких структур и
применение математического аппарата те же самые, как и для нелинейных открытых
физических систем. Большое сходство уравнений для описания этих явлений указывает
на структурный изоморфизм процессов самоорганизации, изучаемых в естественных и
гуманитарных науках.
Учитывая огромное количество реальных систем в природе и обществе,
по одчиняющихся законам синергетики, можно считать, чт создание синергетической
картины мира является по существу научной революцией, сравнимой по своим
масштабам с открытием строения атома, созданием генетики и кибернетики. Синергетика
убедительно показывает, что в самом фундаменте природы, как неживой, так и живой,
заложен принцип «инь» — «янь». Это — принцип развертывания и свертывания,
эволюции и инволюции, развития и угасания, роста и вымирания, хаоса и порядка,
устойчивости — неустойчивости.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какой смысл имеет понятие «бифуркация»?
2. Объясните основные понятия синергетики.
3. Как происходят процессы в открытых системах?
4. Приведите примеры самоорганизации в неживой и живой природе.
5. Что такое диссипативные структуры?
6. Что такое аттракторы?
7. Как Вы представляете детерминированный или динамический хаос?
8. Какие два подхода известны для анализа сложных самоорганизующихся систем?
9. Как можно описать устойчивость—неустойчивость в самоорганизующихся
системах?
10. Как Вы представляете возникновение порядка из хаоса?
11. В чем состоит принцип производства минимума энтропии?
12. Что можно сказать о золотом сечении и законах гармонии?
13. Что понимают под синергетической картиной мира?
14. Почему, на Ваш взгляд, невозможно дать долговременный огноз погоды? пр
15. Как можно связать теорию катастроф с самоорганизацией сложных систем?
16. Что мы понимаем под устойчивым равновесием, неустойчивым?
ЛИТЕРАТУРА
4, 8, 13, 16, 21, 26, 30, 33, 34, 62, 63, 68, 88, 109, 110, 111, 123, 125, 149, 158.
215
Глава 8. СИММЕТРИЯ И АСИММЕТРИЯ В РАЗЛИЧНЫХ
ФИЗИЧЕСКИХ ПРОЯВЛЕНИЯХ
Состояние равно ичным весия должно быть, по-видимому, симметр
Г:Вейль
Природа менее симметрична, чем можно было бы ожидать исходя из
уравнений классической и квантовой физики.
И. Пригожин
Понятия симметрии и противоположного ей объективного свойства природы —
асимметрии являются одними из фундаментальных в современном естествознании.
Поэтому научные исследования общеглобального характера в значительной степени
основываются на рассмотрении указанных понятий. Негласный лозунг физиков-
теоретиков: «правильная теория олжна быть красиво » — находит свое место в д й
построении новых теоретических моделей и связан зачастую с симметрийными
представлениями, а эстетический фактор играет при этом не последне значение. е
Симметрия является одним из фундаментальных свойств природы, представление о
ней складывалось в течение жизни десятков сотен и тысяч поколений людей. Как говорил
наш известный кристаллограф А. В. Шубников (1887—1970), посвятивший изучению
симметрии всю свою жизнь, «изучение археологических памятников показывает, что

Янко Слава (Библиотека Fort/Da) || http://yanko.lib.ru
Горбачев В. В. Концепции современного естествознания:—М.: ООО «Издательский дом «ОНИКС 21
век»: ООО «Издательство «Мир и Образование», 2003. — 592 с: ил.
132
человечество на заре своей культуры уже имело представление о симметрии и
осуществляло ее в рисунке и в предметах быта. Надо полагать, что применение
симметрии в первобытном производстве определялось не только эстетическими
мотивами, но в известной мере и уверенностью человека в большей пригодности для
практики правильных форм». Быть прекрасным, говорил Платон, «значит быть
симметричным и соразмерным».
Интуитивно симметрия в своих простых формах понятна любому человеку, и часто
мы выделяем ее как элемент прекрасного и совершенного. В известной мере симметрия
отражает степень упорядоченности системы. Например, окружность, ограничивающая
каплю на плоскости, более упорядочена, чем размытое пятно на этой же площади, и,
следовательно, более симметрична. Поэтому можно связать изменение энтропии как
характеристики упорядочения с симметрией: чем более организовано вещество, тем
выше симметрия и тем меньше энтропия.
216
Одно из определений понятий симметрии и асимметрии дал В. Готт: симметрия —
понятие, отражающее существующий в природе порядок, пропорциональность и
соразмерность между элементами какой-либо системы или объекта природы,
упорядоченност , равновесие системы, устойчивость, т.е., ес и хотите, неки элемент ь л й
гармонии. Другое определение дал Г. Вейль: «Симметричным является предмет, с
которым можно сделать нечто, не изменяя этого предмета». Асимметрия — понятие
противоположное симметрии, отражающее разупорядочение системы, нарушение
равновесия, что связано с изменением, развитием системы. Из соображений симметрии-
асимметрии приходят к выводу, что развивающаяся динамическая система должна быть
неравновесной и несимметричной. В ряде случаев симметрия является достаточно
очевидным фактом. Например, для определенных геометрических фигур не трудно
увидеть эту симметрию и показать ее путем соответствующих преобразований, в
результате которых фигура не изменит своего вида.
Симметрия проявляется не только в понимании геометрического строения тел в
природе, но и в ряде областей человеческой деятельности. Симметрия существует в
музыке, хореографии (например, в болеро Равеля многие народные песни и танцы
построены симметрично), в зеркальной симметрии текста (любопытно, что при
горизонтальной оси симметрии буквы зеркально отражаются и «читаются», а при
вертикальной оси симметрии — нет), в начертании знаков языка (например, в китайской
письменности имеется иероглиф, означающий истинную середину), архитектуре,
живописи, математике, огике, строении живых организмов и растений и др. В. И. л
Вернадский справедливо отмечал: «Новым в науке явилось не выявление принципа
симметрии, а выявление его всеобщности».
Для живых организмов симметричное расположение частей органов тела помогает
сохранять им равновесие при передвижении и функционировании, обеспечивает их
жизнестойкость и лучшее приспособление к окружающему миру, что справедливо и в
растительном мире. Например, ствол ели или сосны чаще всего прям и ветви равномерно
расположены относительно ствола. Так дерево, развиваясь в условиях действия силы
тяжести, достигает устойчивого положения. К вершине дерева ветви его становятся
меньше в размерах — оно приобретает форму конуса, поскольку на нижние ветви, как и
на верхние, должен падать свет. Кроме того, центр тяжести должен быть как можно
ниже, от этого зависит устойчивость дерева.
217
Законы естественного отбора и всемирного тяготения способствовали тому, что
дерево не только эстетически красиво, но устроено целесообразно. Получается, что
симметрия живых организмов связана с симметрией законов природы. На житейском
уровне, когда мы видим проявление симметрии в живой и неживой природе, то невольно
испытываем чувство удовлетворения тем всеобщим, как нам кажется, порядком, который
царит в природе.
Однако понятие симметрии гораздо шире и ее можно понимать как неизменность
(инвариантность) каких-либо свойств объекта по отношению к преобразованиям,
операциям, выполняемым над этим объектом. Причем это может быть не только
материальный объект, но и закон, математическая формула или уравнения, в том числе и
нелинейные, которые (см. гл. 7) играют большую роль в самоорганизующихся процессах.
Дать более конкретное определение симметрии, чем у Готта, в общем случае
затруднительно еще и потому, что она принимает свою форму в каждой сфере
человеческой деятельности. В искусстве симметрия может проявиться в соразмерности и

Янко Слава (Библиотека Fort/Da) || http://yanko.lib.ru
Горбачев В. В. Концепции современного естествознания:—М.: ООО «Издательский дом «ОНИКС 21
век»: ООО «Издательство «Мир и Образование», 2003. — 592 с: ил.
133
взаимосвязанности, гармонизации отдельных частей в целом произведении. В
математических построениях также имеют мест симметричные многочлены, которые о
можно использовать для существенного упрощения решения алгебраических и
дифференциальных уравнений. Особенно полезным оказало ь использован е с и
симметрийных представлений в еории груп с введени м инварианта, т.е. такого т п е
преобразования, когда соотношения между переменными не изменяются. Отражением
связи пространства, симметрии и законов сохранения может служить мысль великого
французского математика А.Пуанкаре: «Пространство — это группа».
Наиболее наглядное и непосредственное применение идей симметрии имеет место в
кристаллографии и физике твердого тела, изучающих физические свойства кристаллов в
зависимости от их строения. Даже непосвященному человеку хорошо видна здесь
ассоциация с неким совершенством, порядком и гармонией. Идеи симметрии являются
для мира кристаллов естественной базой их физической сущности. Один из создателей
современной физики твердого тела Дж. Займен вообще считал, что вся теория твердых
тел основана на трансляционной симметрии. Здесь симметрия проявляется при
совмещении геометрических тел, например правильных многогранников, при повороте
их в
218
пространстве на определенные углы, а также при перемещениях в атомной решетке на
определенные величины векторов трансляции, кратных периоду решетки:
где а — период решетки кристалла, — модуль волнового вектора, Ε — энергия
кр
8.1. Симметрия и законы сохранения
исталлической решетки.
Более глубокое по гл. 2) с изучением и нимание и применение симметрии связано (см.
обоснованием законов сохранения, отражающих фундаментальные свойства
пространства— ремени. Н помним, что мметрия относительно произвольн о сдвига в а си ог
во времени приводит к закону сохранения энергии для консервативных (замкнутых)
систем:
Ε = const.
Неизменность характеристик физической системы при произвольном перемещении ее
как целого в пространстве на произвольный вектор приводит к закону сохранения
импульса р:
И наконец, симметрия относительно произвольных пространственных поворотов
(изотропность пространства) связана с законом сохранения момента импульса:
Общие законы природы, характеризующие движение материи, связаны с симметрией
пространства и времени. Время само по себе не способно изменить энергию какой-либо
системы. Закон сохранения энергии есть следствие однородности времени. Закон
сохранения импульса есть следствие однородности пространства.
Так как категория симметрии относится к любому объекту или понятию, то она в
полной мере применима, например, к физическому закону. А поскольку цель физических
законов — нахождение и вычисление идентичного в явлениях, то для инер-
219
циальных систем, согласно принципу относительности Галилея, эти физические
законы будут во всех системах одинаковы. Следовательно, они инвариантны
относительно описания явлений как в дной инерциальной системе, так и в другой и тем о
самым сохраняют симметрию. В 1918 г. были доказаны теоремы Э. Нетер, смысл одной
из которых состоит в том, что различным видам симметрии физических законов
соответствуют определенные законы сохранения. Эта связь является настолько всеобщей,
что ее можно считать наиболее полным отображением понятия сохранения субстанций и
законов, ее описывающих, в природе. Как сказал Р. Фейнман, «среди мудрейших и
удивительных вещей в физике эта связь — одна из самых красивых и удивительных».
Различие видов симметрии связано с разными способами пространственно-временного
преобразования одной инерциальной системы в другую инерциальную систему.

Янко Слава (Библиотека Fort/Da) || http://yanko.lib.ru
Горбачев В. В. Концепции современного естествознания:—М.: ООО «Издательский дом «ОНИКС 21
век»: ООО «Издательство «Мир и Образование», 2003. — 592 с: ил.
134
Остановимся на этом несколько подробнее. Каждому такому пространственно-
временному преобразованию соответствует определенный вид симметрии. Так, перенос
начала координат в произвольную точку пространства при неизменности физических
свойств или их проявлении связан с симметрией таких преобразований (это как раз и есть
трансляционная симметрия) и означает физическую эквивалентность всех точек
пространства, т.е его однородность. .
Поворот координатных осей в пространстве связан с физической эквивалентностью
разных направлений в пространстве и означает изотропность пространства. Симметрия
относительно переноса во времени связана с физической эквивалентностью различных
моментов времени, что должно также отражать идею независимости хода времени от его
начала (время протекает одинаково). Поэтому однородность времени проявляется в его
равномерном течении, а относительная скорость всех процессов, протекающих в
природе, одинакова. Факт равномерности течения времени был установлен
экспериментально с точностью до 10
-14
с за ериод ~10 миллионов лет например, п ;
спектральный состав излучения звезд, испущенного миллионы лет назад и
воспринимаемого нами олько сейча , имеет одинаковый сп ктральный оста таких е т с е с в ж
атомов на Земле.
В классической релятивистской механике симметрия выражается в принципе
отн и е ос тельности. Равномерное и прямолинейное движени материальной точки в
инерциальной системе отсчета с произвольной скоростью, но меньшей, чем скорость све-
220
та, связано с симметрией и физической эквивалентностью такого движения и покоя
(неразличимость параметров движения объекта в движущемся равномерно и
прямолинейно поезде и поезде, стоящем еподвижно а путях). Как мы знаем, при н н
скоростях V << с используют принцип относительности и преобразования Галилея, при V
≈ с (релятивистские скорости) — принцип относительности Эйнштейна и преобразования
Лоренца. Такого рода симметрию (неразличимость покоя и равномерно-прямолинейного
движения) можно условно определить как изотропию пространства—времени. Эти виды
симметрии объединяются в СТО в единую симметрию четырехмерного пространства—
времени.
8.2. Симметрия—асимметрия
Проблемы симметрии язанными между собой —асимметрии оказываются тесно св
глубже, чем это кажется, исходя из бинарной структуры этих понятий (да — нет).
Примером может служить состояние человека во вращающейся центрифуге. Существует
симметрия вращения (поворота), но относительность покоя и вращательного движения
нарушается и человек в такой центрифуге по своему состоянию (вестибулярные
ощущения) может отличить, что его вращающаяся закрытая (герметизированная) камера
на центрифуге вращается. Таким образом, возникает ситуация, при которой физические
законы не инвариантны относительно вращения, т.е. налицо асимметрия.
Асимметрия относительно масштабных преобразований при изменении масштабов
физических систем связана с тем, что порядок размеров атомов имеет одинаковое для
всей нашей Вселенной значение (~10
-10
м). Если уменьшить масштабы размеров,
например, изделий микроэлектроники, в том числе и пленочных, то характер поведения
электронов в них изменится (возникнут размерные эффекты), т.е. опять-таки может
появиться асимметричность процессов при таких размерах. Другой пример несимметрии
относительно масштабов можно привести из биологии: несмотря на похожесть окраски,
нельзя, например, раскормить осу до размеров тигра, так как при массе 10—100 кг она
потеряет способность летать — возникнет другое качество.
Рассмотрим другие виды симметрии. Упомянутые выше пространственно-временные
виды симметрии условно объединяет одно общее свойство: они являются как бы
«внешними» симмет-
221
риями, так как отражают глубокие свойства структуры пространства—времени,
представляющие собой форму существования любого вида материи, и поэтому
справедливые для любы мыслимых взаимодействий и физических процессов. Весь х
физический опыт познания мира показывает отсутствие нарушений инвариантности
законов природы относительно указанных пространственно-временных преобразований.
В этом уже не только физический, но и философский смысл познания и установления
объективности законов природы.
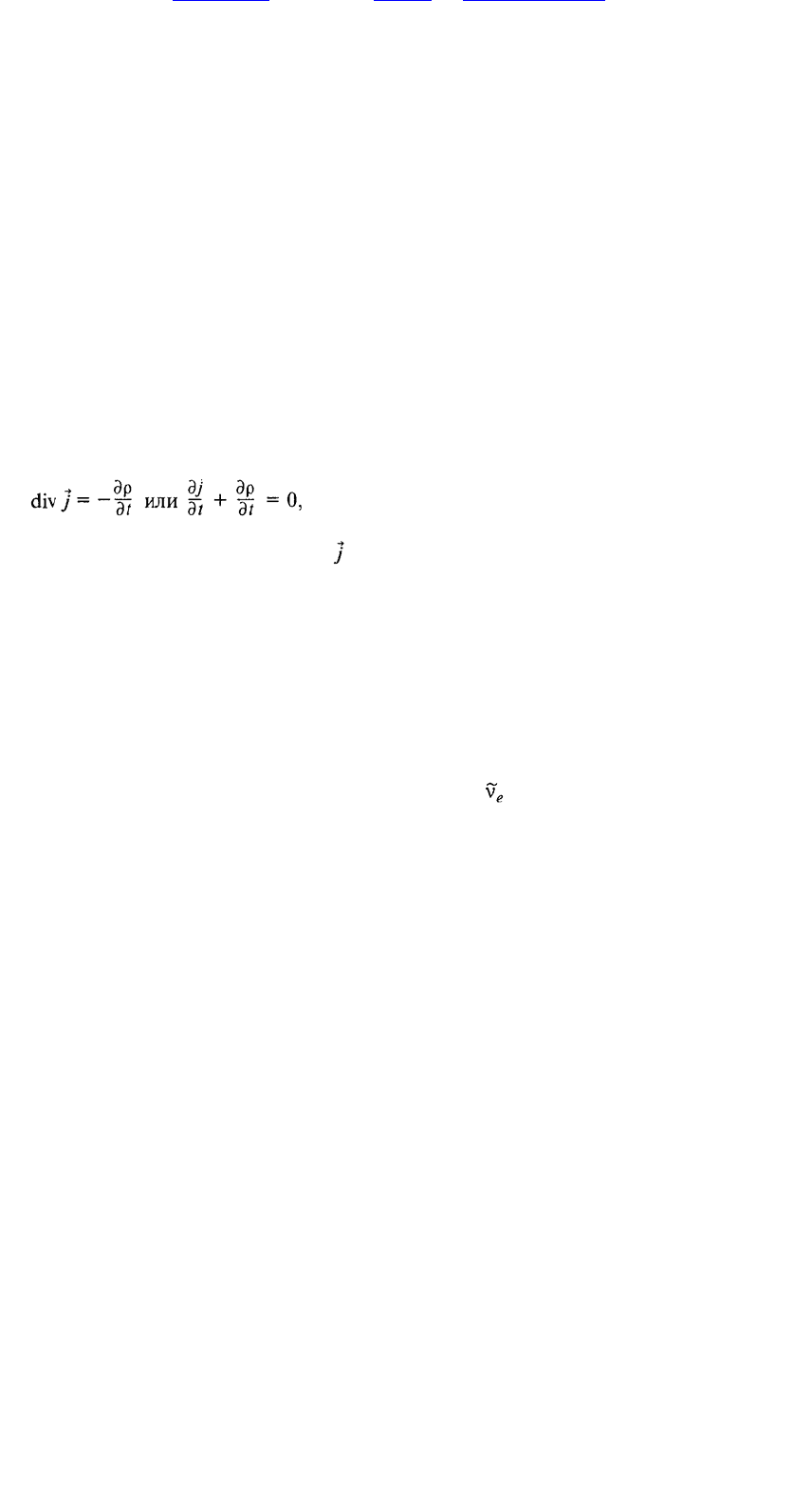
Янко Слава (Библиотека Fort/Da) || http://yanko.lib.ru
Горбачев В. В. Концепции современного естествознания:—М.: ООО «Издательский дом «ОНИКС 21
век»: ООО «Издательство «Мир и Образование», 2003. — 592 с: ил.
135
Однако во «внешних» симметриях не затрагивается «внутренний мир» физического
объекта, который никак не связан с внешними свойствами. В природе кроме
рассмотренных законов сохранения энергии, импульса и момента импу ьса существуют л
и другие законы сохранения, которые выполняются с той или иной степенью общности, в
частности закон сохранения электрического заряда. В физике фундаментальных частиц
имеются и другие сохраняющиеся (или по крайней мере введенные так) величины,
подобные электрическому заряду — барионное число, четность, изоспин, ароматы
(странность, очарование, красота и др.). Они, по сути, квантовые числа, связаны
фазовыми преобразованиями волновой функции ψ и не зависят от свойства
пространства—времени. Симметрия играет важную роль в исследов нии физики а
микромира. Наш физик-теоретик А. Мигдал считал, что главными направлениями физики
ХХ в. были поиски симметрии и единства картины мира.
Сохранение подобных величин, непосредственно не связанных со свойствами
пр
8.3. Закон сохранения электрического заряда
остранства—времени, относится к понятию «внутренней» симметрии.
Рассмотрим о в том, что закон сохранения электрического заряда. Смысл ег
алг себраическая умма зарядов любой электрически изолированной системы сохраняется
во времени:
где j — плотность тока, ρ — объемная плотность заряда. Физический смысл этого
уравнения состоит в том, что div — расходимость тока (его движение) связана с
изменением во времени, т.е. перемещением электрического заряда. Математический
смысл
222
закона сохранения заряда заключен в уравнении непрерывности. Электрический ток
— направленное движение свободных заряженных частиц в электрическом поле.
Физический смысл закона сохранения заряда отражает факт несотворимости и
неуничтожимости электрического заряда.
Нужно подчеркнуть, что сохранение электрического заряда в изолированных
(замкнутых) системах не сводится к сохранению числа заряженных частиц. Так при β
распаде нейтрона, не имеющего заряда, n -> p + е
-
+ возникают протон (с зарядом е
+
),
электрон (заряд е~) и антинейтрино, также не имеюще заряда. В этой реакции появились е
две электрически заряженные частицы, но их суммарный заряд равен нулю, как и у
породившего их нейтрона. Отметим, что важным следствием закона сохранения заряда
является устойчивость электрона. Электрон является самой легкой электрически
заряженной частицей. Поэтому ему просто не н что распадаться, так как в этом случае а
нарушился бы закон сохранения электрического заряда. По современным
представлен ям, емя жизни электрон не менее 10
19
ле , что говорит пользу этого и вр а т в
закона.
8.4. Зеркальная симметрия
Прежде чем перейти к д остановимся еще на двух ругим «внутренним» симметриям
видах дискретной симметрии, которые отличаются от непрерывных симметрий сдвига и
поворота. Рассмотрим зеркальную симметрию, которая описывается пространственной
инверсией, т.е. отражением системы координатных осей. Инверсия пространства
осуществляется «сразу» (в зеркале), а е повторное применение возвращ ет систему в е а
исходное состояние. Это отражение называется операцией изменения «четности»
(пример с теннисистом в зеркале). Другой дискретной симметрией является симметрия
относительного обращения времени, приводящая к тому, что в симметричной Вселенной
законы природы не изменяются при замене направления течения времени на обратное (t
тождественно равно —t и наоборот). Применение данной симметрии показывает, что
направление возрастания времени (движение в одну сторону) не играет существенной
роли. С равной вероятностью возможен и обратный процесс. Другими словами,
установить путем наблюдения, происходит ли развития событий в будущее или в
прошлое, для
223
равновесной симметричной системы невозможно. К такому же результату приводит
детерминированная механика Галилея — Ньютона в замкнутых системах. Но

Янко Слава (Библиотека Fort/Da) || http://yanko.lib.ru
Горбачев В. В. Концепции современного естествознания:—М.: ООО «Издательский дом «ОНИКС 21
век»: ООО «Издательство «Мир и Образование», 2003. — 592 с: ил.
136
одновременно мы уже знаем о существовании «стрелы времени» для открытых и
неравновесных систем. И это еще раз показывает неумолимо, что время все-таки «течет»
от прошлого к будущему и наша Вселенная неравновесна и асимметрична. Заметим,
однако, что понятие энтропии не однозначно применимо к микромиру и, следовательно,
изучая его, нельзя установить направление времени.
8.5. Другие виды симметрии
Дальнейшее расширени ий связано с развитием е количества физических симметр
квантовой механики. Одним из специальных видов симметрии в микромире является
перестановочная симметрия. Она основана на принципиальной неразличимости
одинаковых микрочастиц, которые движутся не по определенным траекториям, а их
положения оцениваются по вероятностным характеристикам, связанным с квадратом
модуля волновой функции. Перестановочная симметрия и заключается в том, что при
«перестановке» квантовых частиц не изменяются вероятностные характеристики, квадрат
модуля волновой функции — величина постоянная |ψ|
2
= const.
Исследование реакций с участием элементарных частиц и античастиц, а также
процессов их распада привело к открытию некоторых новых свойств симметрии, а
именно зарядовой симметрии или, более точно, зарядовой симметрии частиц и
античастиц. При изучении ядерных взаимодействий нуклонов (сильные взаимодействия)
было обнаружено, что эти ядерные силы почти не зависят от типа нуклонов, т.е. при этих
взаимодействиях нет различия между нейтроном и протоном, оба они есть два состояния
одной частицы — нуклона. Аналогично, μ мезон может находиться в трех состояниях,
соответствующих трем различным частицам. Такие состояния называются
изотопическими, и они характеризуютс изотопическим спином, или изоспином (см. я
табл. 6.2). Симметрия, связанная с этими процессами, и получила название
изотопической симметрии .
С теорией элементарных частиц, типами взаимодействия полей и попыткой
по о встр ения теории единого поля, связаны еще д а вида симметрии: кварк-лептонная и
калибровочная. Кварк-лептонная симметрия проявляется в единой теории поля.
224
Считается, что по существу кварки и лептоны неразличимы в области очень больших
энергий. Но в случае спонтанного нарушения симметрии и в области низких энергий они
приобретают совершенно различные свойства. Тем самым установлено, что между
кварками и лептонами возможны переходы. Этот факт может служить еще одним
убедительным доказательством единства природы.
Калибровочная симметрия связана с масштабными преобразованиями,
пр сд у ка о едставляющими виги нулевых ровней с лярного и векторног потенциалов полей.
Термин «калибровочное поле» (преобразование, инвариантность) выдвинул немецкий
математик Г. Вейль (1885—1955). Смысл идеи состоит в том, что физические законы не
должны зависеть от масштаба длины, выбранного в пространстве, и не должны изменять
свой вид при замене этого масштаба на любой другой. С обычной логикой это вроде бы
самоочевидно: почему, действительно, законы Ньютона будут другими, если мы будем
измерять путь в метрах, сантиметрах или в мегапарсеках?! Однако значение изменения
масштаба состоит в том, что оно имеет принципиально нефизический характер, т.к. не
вызвано какими-либо физическими воздействиями, а геометрический характер, в
частности изменение длины, обусловлен лишь особенностями структуры пространства—
времени. Тем самым пространство—время перестает быть лишь пассивным резервуаром
вещества и поля, где происходят физические процессы, оно само начинает активно
влиять на эти процессы. Геометрия приобретет динамический характер.
Особое значение приобретает принцип калибровочной инвариантности, если
пр аеобразов ния проходят локально в каждой точке пространства—времени и
неоднородно, т. . с изменяющимся соотношением от точки к точке. Вот э о е т
преобразовани Г. Вей ь и назвал масштабным или калибровочным. Его формулировка е л
звучит так: все физические законы инвариантны относительно произвольных
(однородных неоднородных) локальных преобразований. В таком виде и калибровочных
принцип Вейля является, по существу, развитием общего принципа относительности
Эйнштейна, что все физические законы в любой системе отсчета (инерциальной и
неинерциальной) должны иметь одинаковый вид. Уместно в связи с этим заметить, что
теория Эйнштейна была первой теорией, в которой геометрический фактор (искривление
пространства—времени) напрямую связывался с физической характеристикой

Янко Слава (Библиотека Fort/Da) || http://yanko.lib.ru
Горбачев В. В. Концепции современного естествознания:—М.: ООО «Издательский дом «ОНИКС 21
век»: ООО «Издательство «Мир и Образование», 2003. — 592 с: ил.
137
(гравитационной
225
массой), что послужило в настоящее время дальнейшему развитию идей
геометродинамики т е. Эти преобразования масш аба оставляют силовы характеристики
поля (например Ε иι В для электромагнитного поля) неизменными. На основе
калибровочной симметрии построены теории электрослабого и электросильного
взаимодействий.
В последние десятилетия прошлого уже века стала развиваться модель
суп с о , аер имметрии, к торая, кстати была предложена нашими теоретиками Гельф ндом и
Лихтманом. Упрощенно говоря, их идея состояла в том, что, подобно тому как
существуют обычные размерности пространства и времени, должны иметься экстра-
размерности, которые можно измерить в так называемых числах Грассмана. Мы уже
говорили ранее о в общем-то трудно-воспринимаемой возможности существования
многомерности пространства. Но, как говорил С. Хокинг, даже научные фантасты не
додумались до чего-нибудь столь же странного, как размерности Грассмана. В нашей
обычной арифметике, если число 4 умножить на 6, — это то же самое, что 6 умножить на
4. Но странность чисел Грассмана состоит в том, что если X умножить на Υ, то это равно
минус Υ умножить на X. Чувствуете, как это далеко от наших классических
представлений о природе и методах ее описания?
Вопросы симметрии играют решающую роль в современной физике. Динамические
законы природы характеризуются определенными видами симметрии. В общем смысле
под симметрией физических законов подразумевают их инвариантность по отношению к
определенным преобразованиям. Необходимо также отметить, что рассмотренные типы
симметрий имеют определенные границы применимости. Например, симметрия правого
и левого существует только в области сильных электромагнитных взаимодействий, но
нарушается при слабых. Изотопическая инвариантность справедлива только при учете
электромагнитных сил. Для применения понятия симметрии в физике можно ввести
некую структуру, учитывающую четыре фактора:
• Объект или явление, которое исследуется.
• Преобразование, по отношению к которому рассматривается симметрия.
• Инвариантность каких-либо свойств объекта или явления, выражающая
рас и х сматриваемую симметрию. Связь симметрии физ чески законов с законами
сохранения.
• Границы применимости различных видов симметрии.
226
Изучение свойств симметрии физических систем или законов требует привлечения
специального математического анализа, в первую очередь представлений теории групп,
наиболее развитой в настоящее время в физике твердого тела и кристаллографии.
В целом же из законов сохранения, которые являются следствием пространственно-
временной симметрии законов самой природы, следует условность разделения физики на
механику, термодинамику, электродинамику и т.д., и, следовательно, налицо
неразрывность единства всей рироды. п
8.6. Хиральность живой и неживой природы
Не останавли , которая будет ваясь здесь более подробно на понятиях физики живого
подробно рассмотрена во второй части, обсудим кратко идеи симметрии—асимметрии
применительно к проблемам объектов живой и неживой природы. По существу, это
философский, но с естественно-научной точки зрения вопрос о возникновении, развитии
и сущности жизни. Чем отличаются молекулы «живых веществ» от «неживых»? В какой-
то мере это связано с симметрией, точнее зеркальной симметрией. Если рассмотреть
пример зеркального изображения двух молекул неорганического вещества воды и
органического, но «неживого» вещества — бутилового спирта (рис. 8.1), то
принципиальное различие проявляется в том, что молекула Н
2
O зеркально симметрична,
а молекула спирта зеркально асимметрична. «Левая» и

Янко Слава (Библиотека Fort/Da) || http://yanko.lib.ru
Горбачев В. В. Концепции современного естествознания:—М.: ООО «Издательский дом «ОНИКС 21
век»: ООО «Издательство «Мир и Образование», 2003. — 592 с: ил.
138
Рис. 8.1. Зеркальная симметрия молекул воды (а) и бутилового спирта (б).
227
«правая» молекулы не совпадают, как левая и правая руки человека. Асимметричные
молекулы в химии называют стереоизомерами, а само свойство зеркальной асимметрии
носит название киральности или хиральности (от греческого слова «кир» — рука). Так
вот, выяснилось, что в природе хиральностью обладают и «живые», и «неживые»
молекулы, но «живые» всегда только хиральны, причем «неживые» хиральные молекулы
равновероятно встречаем и в левом, и в правом варианте, а «живые» — только или в
левом, или в правом. В этом смысле молекулы живых организмов хирально чисты. Так,
ориентация ДНК-спирали всегда правая. В свое время Л. Пастер, а затем и В. И.
Вернадский предлагали на этом принципиальном различии провести раздел между живой
и неживой природой.
Предполагают, что основополагающим признаком возникновения и развития жизни и
является способность живых организмов извлекать и конструировать из симметричных и
хирально нечистых молекул окружающей среды хирально чистые молекулы,
необходимые для живого организма. Примером могут служить извлечение растениями из
симметричных молекул воды и углекислого газа в процессе фотосинтеза асимметричных
молекул крахмала и сахара. Наряду с другими питательными веществами эти молекулы
поступают в пищу живых организмов, и из них образуются уже хирально чистые
молекулы. Если хиральность молекул веществ пищи изменится на противоположную, то
эти вещества окажутся для живого организма биологическим ядом, они отторгаются
организмом, ведут его к гибели. Это достаточно характерный пример того, как из
физических представлений симметрии можно объяснить происхождение живой материи
и даже дать рекомендации практической медицине.
В общем смысле мы можем считать, что и возникновение жизни в целом связано со
спонтанным нарушением имевшейся до того в природе зеркальной симметрии.
Предполагают, что возникаемая асимметрия произошла скачком в результате Большого
Биологического Взрыва по аналогии с БВ, в результате которого образовалась Вселенная,
под действием радиации, температуры, полей и т.д. и нашла свое отражение в генах
живых организмов. Этот процесс, по существу, также является процессом
самоорганизации (см. гл. 7). В какой-то точке бифуркации произошел и
самоорганизующий акт возникновения разума уже живой материи.
228
8.7. Симметрия и энтропия
Теперь уместно связать симметрию с энтропией живых организмов. Известно, что
переход вещества на более высокую степень организации, упорядоченности снижает
энтропию как меру хаотичности. Но наибольшей симметрией обладает как раз
равновесное хаотическое состояние. Значит, уменьшение энтропии неизбежно приводит
к уменьшению симметрии, т.е. увеличению асимметрии живых организмов. Чем выше
уровень организации материи, тем меньше энтропия и симметрия. Для снижения
энтропии живых организмов, как открытых систем, обменивающихся энергией и
материей (пища и отправления) с окружающей средой, необходима энергия, причем
значительная, которая вырабатывается в соответствующих частях клеток (митохондриях)
живых организмов за счет пищи, т.е. поглощения энергии внешней среды (Солнца и
биосферы).
Образно выражаясь, мы забираем от природы более организованную
структурированную материю, обладающую меньшей энтропией, т.е. подпитываем себя

Янко Слава (Библиотека Fort/Da) || http://yanko.lib.ru
Горбачев В. В. Концепции современного естествознания:—М.: ООО «Издательский дом «ОНИКС 21
век»: ООО «Издательство «Мир и Образование», 2003. — 592 с: ил.
139
негэнтропией, а отдаем ей неструктурированную материю, обладающую большей
энтропией. «Питаемся», с энергетической физической точки зрения, отрицательной
энтропией, а отдаем положительную энтропию. И когда в естественных условиях этот
баланс нарушается, то наступает некоторое динамическое равновесие — обмен
энтропией между человеком и окружающей средой стабилизируется, энтропия системы
человек — окружающая среда возрастает, и живой организм гибнет (энтропия его
возросла). Поэтому биологическая смерть живого организма — это рост энтропии до ее
уровня в окружающей среде. Повышение же энергетического потенциала в живом
организме при «нормальном» обмене энтропией его с окружающей средой увеличивает
химическую активность клеток и дает возможность самовоспроизведения и развития.
По мере упорядочения живых организмов, их усложнения в ходе развития жизни
асимметрия все больше и больше превалирует над симметрией, вытесняя ее из
биохимических и физиологических процессов. Однако и здесь имеет место динамический
процесс: симметрия и асимметрия в функционировании живых организмов тесно
связаны. Внешне человек и животные симметричны, однако их внутреннее строение
существенно асимметрично. Если у низших биологических объектов, например низших
растений, размножение идет симметрично, то у высших имеет
229
место явная асимметрия — разделение полов, где каждый пол вносит в процесс
самовоспроизведения свойственную только ему генетическую информацию. Так,
устойчивое сохранение наследственности есть проявление в известном смысле
симметрии, а в изменчивости же проявляется асимметрия. В целом же глубокая
внутренняя связь симметрии и асимметрии в живой природе обусловливает ее
возникновение, существование и развитие.
Существуют ли другие виды симметрии и связанные с ними законы сохранения? В
чем состоит глубокое значение законов сохранения электрического заряда, лептонного и
барионного чисел, странности, изотопического спина и др.? Как это связано со
свойствами абстрактного пространства? В чем смысл наличия черных дыр как неких
«пропускных пунктов» из нашего пространства в другое? К сожалению, пока на эти
вопросы мы ответа не имеем, хотя и хорошо, что современная наука дает возможность их
задавать.
По поводу задаваемых вопросов существует следующий физический анекдот. В.
Паули очень любил задавать вопросы, на которые не всегда можно найти правильные
ответы (их вообще могло и не быть!). Когда он умер, то продолжал свое любимое занятие
на том свете. И там никто не мог ответить на его вопросы. Тогда он решил обратиться к
Богу. Господь терпеливо и внимательно выслушал его и ответил: «Вся трудность, Паули,
в том, что Вы задаете не те вопросы», и это подтверждает В. Гейзенберг: «Ответ
природы на вопрос исследователя зависит не только от ее устройства, но и от способа
постановки вопроса», и ему вторит И. Пригожин: «Познание мира — это диалог
человека с природой, искусство вопрошать природу и давать ей возможность
ответить на его вопросы».
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие примеры симметрии и асимметрии в неживой и живой природе Вы можете
привести?
2. Обоснуйте связь симметрии с законами сохранения.
3. Какие виды симметрии Вам известны?
4. В чем смысл принципа Вейля?
5. Связана ли гармония с симметрией?
6. Как можно понять природу симметрии?
7. Что такое хиральность молекул объектов живой природы?
8. Какова связь симметрии с энтропией?
9. Как происходит обмен энергией между живым организмом и окружающей средой?
ЛИТЕРАТУРА
26, 59, 71, 75, 88, 115, 131, 134.
230
Глава 9. СОВРЕМЕННАЯ ЕСТЕСТВЕННО-НАУЧНАЯ
КАРТИНА МИРА С ПОЗИЦИИ ФИЗИКИ
Многообразие отдельных законов пронизана некими общими принципами, которые
так или иначе содержатся в каждом законе.
Р. Фейнман

Янко Слава (Библиотека Fort/Da) || http://yanko.lib.ru
Горбачев В. В. Концепции современного естествознания:—М.: ООО «Издательский дом «ОНИКС 21
век»: ООО «Издательство «Мир и Образование», 2003. — 592 с: ил.
140
Природа — сфинкс.
И тем верней своим искусом губит человека,
что, может статься, никакой от века
загадки нет и не было у ней.
Ф. Тютчев
В заключение можно отметить, что физический аспект лежит в основе всего
естествознания. Развитие физики показывает, что происходит непрерывное движение от
понимания отдельных, частных проблем ко все более общим законам природы.
Появление релятивистской механики Эйнштейна отнюдь не отменило классическую
физику Ньютона. Последняя оказалась следствием механики Эйнштейна при условии,
что скорости движения малы по сравнению со скоростью света. Законы
макроскопической механики являются следствием законов квантовой механики,
управляющих микромиром.
На эмоционально-лингвистическом уровне можно в шутку сказать, что Ньютон внес
«новый тон» (new tone) в описание динамических законов природы или вообще построил
целый «новый город» в современной для того времени физике (new town), оправдывая
тем самым свою знаменитую фамилию Newton. А на то, что соответствующие
фундаментальные законы природы вообще должны представлять собой нечто
принципиально единое и незыблемое как некий монолит или один-единственный
краеугольный камень, или короче — просто один камень (ein Stein), — на это обратил
должное внимание как раз Эйнштейн, опять-таки как бы оправдывая, словно по воле
Провидения, свою столь же знаменитую фамилию Einstein.
В современной постнеклассической физике замечено, что с каждым новым шагом
развития ее основные законы и теории как бы упрощаются, становятся более
фундаментальными. Как сказал А. Мигдал, «в науке в отличие от искусства глубокая
мысль выигрывает от упрощения». Естественно, новая теория должна переходить в
старую в тех условиях, для которых эта старая теория была установлена. Это позволяет
отделять, согласно М. Гелл-Манну, возможное от еще не изученного. Ученый дол-
231
жен быть непредвзятым и отказываться от привычных представлений только тогда,
когда новые представления не противоречат установленным фактам. Все большее число
известных ранее законов и положений становится следствием более общих. При этом
старые утверждения, как часть новых, можно вывести, опираясь на законы формальной
логики. Например, по мере развития физики число фундаментальных взаимодействий и
фундаментальных частиц уменьшилось. Почему это происходит, не совсем понятно, но
это исторический факт, который интуитивно еще в XIV в. был осознан францисканским
монахом и философом У. Оккамом и получил название принципа бритвы Оккама. Его
утверждение гласит: «Чем ближе мы находимся к некоторой истине, тем проще
оказываются законы, выражающие эту истину» или: «не приумножай сущностей сверх
необходимого», т.е. объясняй факты простейшим способом. Это одна из аксиом науки.
Возможно, число законов природы конечно, но способы познания их, т.е. наука, остаются
при этом бесконечными. Как сказал Р. Фейнман: «Может быть, вещь проста только
тогда, когда ее можно исчерпывающим образом охарактеризовать несколькими
различными способами, еще не зная, что на самом деле ты говоришь об одном и том
же». Кроме того, познанные законы природы показали, что установление рамок, границ,
в пределах которых действует та или иная физическая модель, также является своего
рода фундаментальным законом. Как сказал Л. Ландау: «Главное в физике — это умение
пренебрегать». По существу, все физические теории, основанные на предыдущих,
надежно установленных и объясненных наукой наблюдениях, сузили круг тех вопросов,
которые можно задавать природе. Как справедливо указывалось в [62], «осознание новых
ограничений стало признаком фундаментальных теорий».
9.1. Классификация механик
Можно представить некоторую образную, взятую из кристаллографических
представлений классификацию фундаментальных физических теорий или механик. Как
предложил А. Зельманов [76], в пространстве трех одинаково нормированных (чтобы не
нарушать симметрию куба) универсальных мировых констант — гравитационной
постоянной G, 1/с и постоянной Планка ft, все механики составляют характерный куб
фундаментальных физических теорий. Каждая механика находится в вер-
