Гончарук Л.И. Методичка - методика расчёта трансформатора

Подождите немного. Документ загружается.

В обмотках, намотанных проводами диаметром менее 0,5 мм, междуслоевая изоляция прокла-

дывается через ряд слоев с суммарным напряжением между крайними слоями U

мс

не более 150 В

мс

= nw

сл

где n — число слоев, между которыми прокладывается междуслойная изоляция;

сл

— число витков в слое;

— напряжение на виток.

В обмотках из проводов диаметром более 0,5 мм междуслоевую изоляцию прокладывают между

всеми слоями.

29. Толщина междуобмоточной изоляции определяется в зависимости от величины испыта-

тельного напряжения обмотки с наибольшим напряжением. При U

исп

до 1000 В рекомендуется при-

менять три слоя бумаги ЭИП-63Б или два слоя бумаги К-12; при U

исп

до 1600 В — соответственно

четыре слоя ЭИП-63Б или три слоя К-12; при U

исп

до 22ОО В – пять слоев ЭИП-63Б или четыре

слоя К-12; при U

исп

до 2700 В — шесть слоев ЭИП-63Б или пять слоев К-12; при U

исп

до

3500 В — восемь слоев ЭИП-63Б или шесть слоев К-12.

30. Количество слоев наружной изоляции выбирается в соответствии с рабочим напряжением

последней обмотки. При U

< 500 В наружную изоляцию выполняют из двух слоев бумаги ЭИП-

63Б или К-12 и одного слоя батистовой ленты толщиной 0,16 мм. При Uр > 500 В наружную изоля-

цию увеличивают на один слой бумаги на каждые 250 В.

31. Число витков в одном слое каждой обмотки находим по формуле

уизп

⋅

1 . р

(33)

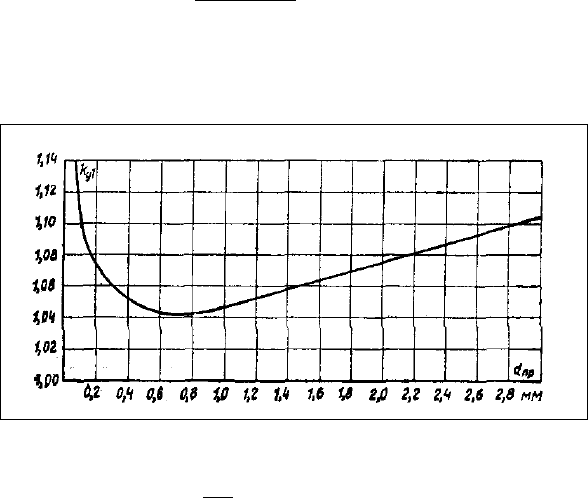
где k

у1

— коэффициент укладки провода в осевом направлении, определяется по кривой на рис. 22;

и d

из пр

— определены ранее.

Если w получается дробным, то его округляют до ближайшего меньшего целого числа.

32. Число слоев определяем из выражения

сл

= . (34)

Под величиной w в выражении (34) понимают для броневых и стержневых однокатушечных

трансформаторов полное число витков обмотки; для стержневых двухкатушечных

трансформаторов — половинное число витков обмотки. Количество N

сл

округляют до ближайшего

большего целого числа.

33. Радиальный размер каждой обмотки при диаметре провода d

пр

с изоляцией больше 0,5 мм

вычисляем по формуле

= k

у 2

сл

из пр

+ k

мс

сл

- 1) h

из мс

, мм. (35)

При диаметре провода с изоляцией меньше 0,5 мм во втором члене выражения (35) следует вме-

сто (N

сл

- 1) подставлять (

150

- 1 ) , округляя полученный коэффициент до большего целого чис-

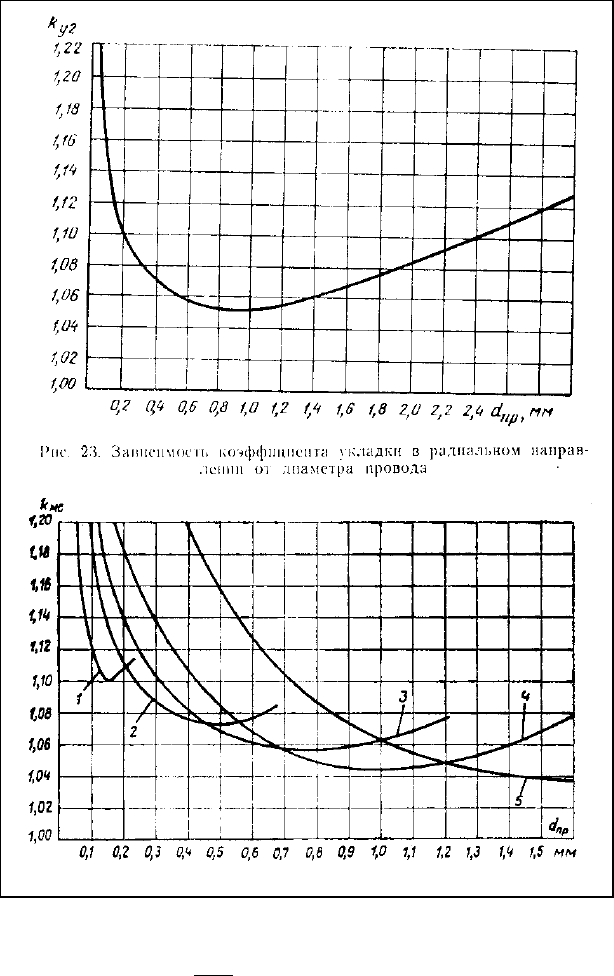
ла. Величину коэффициента укладки в радиальном направлении k

у 2

в зависимости от диаметра

провода определяют по рис. 23. Толщину междуслойной изоляции h

из мс

определяют на основании

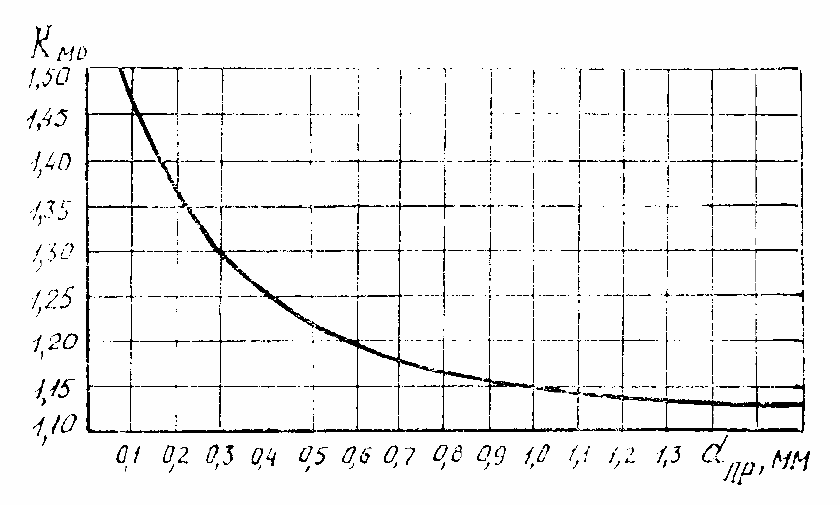
приведенных выше рекомендаций; коэффициент неплотности междуслоевой изоляции k

мс

опреде-

ляется по кривым, приведенным на рис. 24, в зависимости от диаметра провода и толщины изоля-

ции результаты расчетов обмоток целесообразно свести в табл. 13.

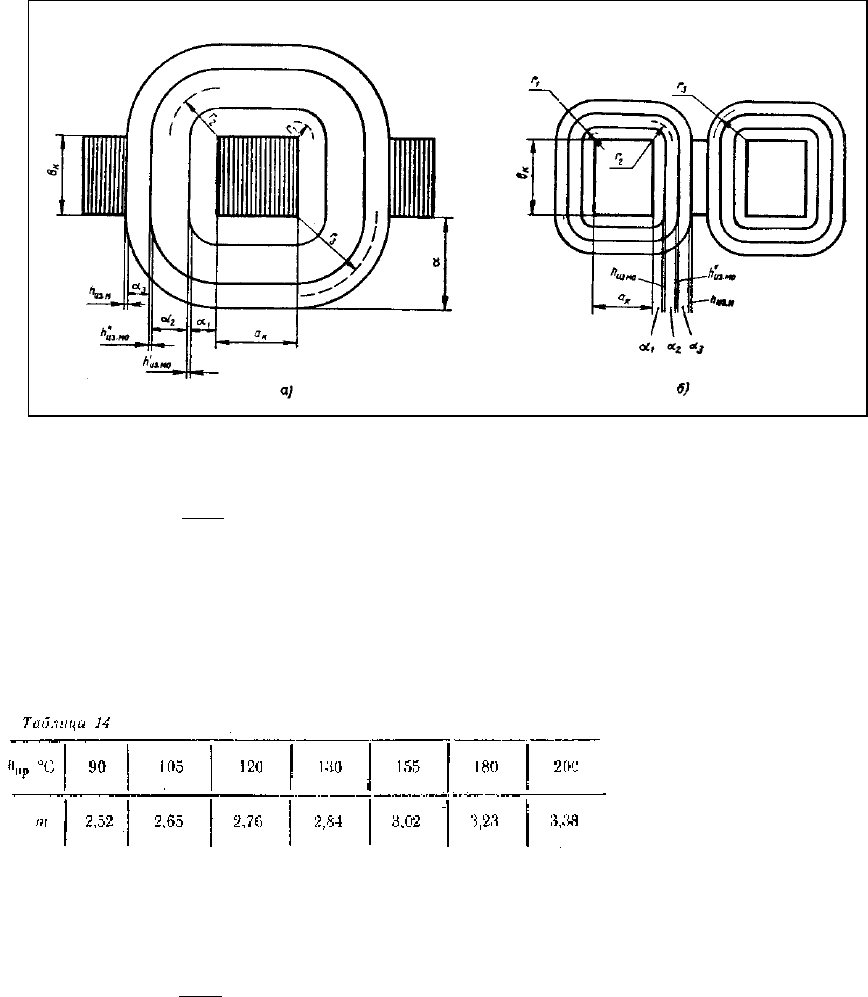
34. Полный радиальный размер катушки определяется из выражения для чередования обмо-

ток 1, 2, 3

кат

= Δ

+ (h

из ос

+ α

+ k

мо

h’

из мо

+ α

+ k

мо

h’’

из мо

+ α

+ k

но

из н

, (36)

где Δ

— зазор между гильзой (каркасом) и сердечником, принимается 0,5 мм;

из ос

— толщина гильзы (каркаса) с учетом дополнительной изоляции поверх каркаса, мм;

, α

— радиальные размеры обмоток, мм;

из н

— толщина наружной изоляции, мм;

h’

из мо

, h’’

из мо

— толщина междуобмоточной изоляции, мм;

мо

— коэффициент неплотности междуобмоточ-

ной изоляции, определяется по рис. 25;

— коэффициент выпучивания (учитывается только при выполнении обмотки на гильзе)

в радиальном направлении; определяется по рис. 26 в зависимости от диаметра про-

вода с учетом отношения b/а выбранного типоразмера магнитопровода (при выполнении

обмотки на каркасе принимается k

=1);

но

— коэффициент неплотности намотки наружной изоляции, принимается равным 1,7 — 2.

Для чередования обмоток 2, 1, 3

кат

= Δ

+ (h

из ос

+ α

+ k

мо

h’’

из мо

+ α

+ k

мо

h’

из мо

+ α

+ k

но

из н

. (36’)

35. Определяем зазор между катушкой и сердечником (для броневых трансформаторов) или

двумя катушками (для стержневых трансформаторов). Если величина этого зазора, равная с - а

кат

для броневых трансформаторов и с - 2а

кат

для стержневых трансформаторов, лежит в пределах от

0,5 до 1 мм, то катушка нормально укладывается в окне магнитопровода. Если полученный зазор

меньше указанного, то необходимо уточнить значение k

ок

и вернуться к п. 4 расчета. В случае при-

менения пластин нестандартных размеров можно увеличить площадь окна в пределах соотношения

h/с = 2 — 3 и уточнить Р

ст

по (13), G

ст

по (15), Q по (17) и I

по (27) и (28) .

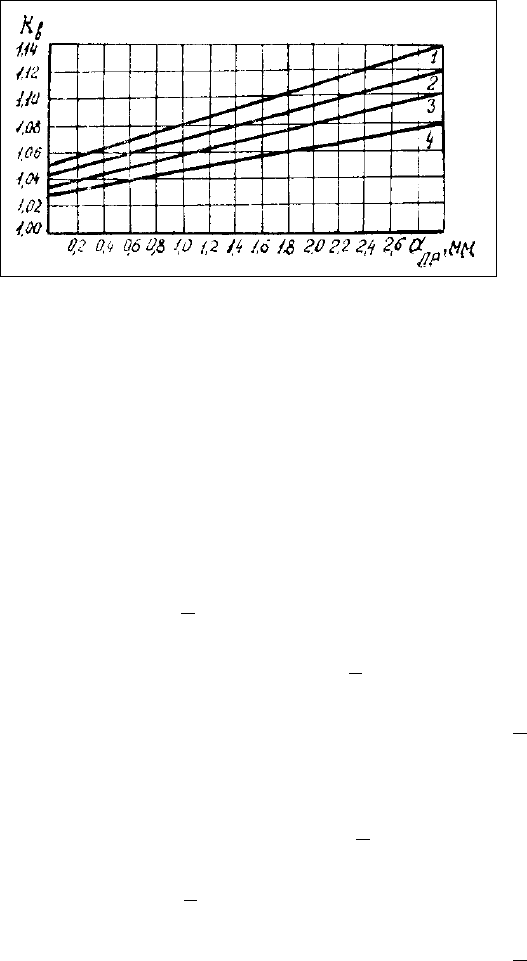
36. Находим среднюю длину витка обмоток. Средняя длина витка может быть определена на

основании рис. 27, а — для броневых и рис. 27,б — для стержневых трансформаторов из выраже-

ний, м:

ср в 1

= [2(a

+ b

) + 2πr

]⋅10

-3

, (37)

где a

и b

— наружные размеры каркаса или гильзы, мм;

= а + 2Δ

+ 2h

из ос

; (38)

= b + 2Δ

+ 2h

из ос

; (39)

— зазор между гильзой (каркасом) и сердечником, мм, см. формулу (36);

ср в 2

= [2(a

+ b

) + 2πr

]⋅10

-3

, (40)

ср в 3

= [2(a

+ b

) + 2πr

]⋅10

-3

, (41)

Когда обмотки наматываются в последовательности 1-я, 2-я, 3-я, значения r

, r

определя-

ются по формулам:

в11

=α ,

мм ; (42)

rhk k

из мо мо в21 2

=+ +(' ),

αα мм ; (43)

rhk hk k

из мо мо из мо мо в31 2 3

=+ ++ +(' '' ),

αα α

мм . (44)

При намотке обмоток в последовательности 2-я, 1-я, 3-я значения r

, r

определяются по фор-

мулам:

rhk k

из мо мо в12 1

=+ +('' ),

αα мм ; (42’)

в22

=α ,

мм ; (43’)

rhkhk k

из мо мо из мо мо в32 1 3

=+ ++ +(' '' ),

αα α

мм . (44’)

37. Массу меди каждой обмотки находим из выражения

= l

ср в

пр

⋅10

-3

, кг. (45)

где l

ср в

— средняя длина витка, м;

w — общее число витков обмотки;

пр

— масса 1м провода, г (берется из прил. П. 1, [5]).

Общую массу провода катушки находим суммированием масс отдельных обмоток.

Проверяем значение α:

α=

cт

Если полученное значение α не лежит в рекомендованных пределах, то необходимо уточнить

расчет с учетом рекомендаций в п. 46.

38. Находим потери в каждой обмотке по формуле

м i

= mj

i факт

м i

, (46)

где m — коэффициент, зависящий от температуры нагрева провода, определяется по табл. 14

по наименьшей из допустимых температур для выбранных проводов обмоток трансформатора.

Потери в катушках равны сумме потерь в отдельных обмотках:

= Р

м1

+ Р

м2

+ Р

м3

. (47)

Проверяем значение β:

β=

cт

Если полученное значение β не лежит в рекомендованных пределах, то необходимо изменить

плотность тока в обмотках j и индукцию В в сердечнике, как рекомендовано в п. 46.

39. Тепловой расчет трансформатора производится по методу электротепловых аналогий,

изложенному в [2]. В этом методе используется формальная аналогия между процессами переноса

тепла и электричества. При этом распределенные

тепловые параметры трансформатора моделиру-

ются сосредоточенными электрическими параметрами, распределенные источники тепла — сосре-

доточенными источниками электрических потерь и распределенные тепловые сопротивле-

ния — сосредоточенными активными сопротивлениями. Затем составляется электрическая схема,

моделирующая процессы теплопередачи в трансформаторе.

Для такой схемы на основании законов Кирхгофа можно составить систему алгебраических

уравнений, при решении которой устанавливается связь между потенциалами (температурами на-

грева), токами (тепловыми потоками) и сопротивлениями (тепловыми сопротивлениями) для узло-

вых точек схемы катушки и сердечника).

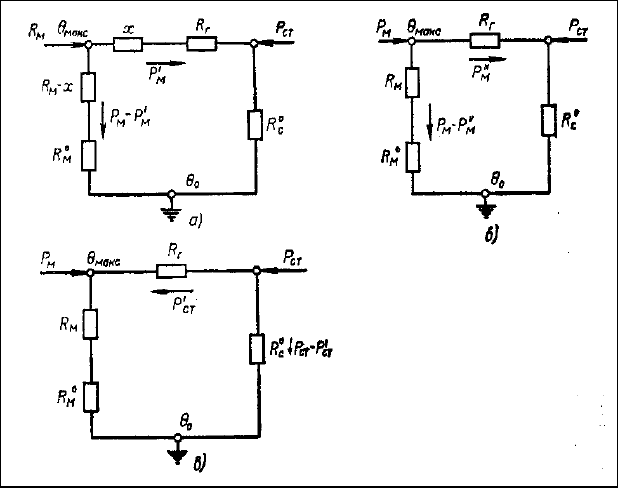
Для определения максимального превышения температуры катушки и максимального значения

среднеобъемной температуры обмотки можно использовать

тепловую схему, изображенную на рис.

28.

На этом рисунке приняты следующие обозначения:

— тепловой поток, мощность которого равна электрическим потерям в обмотке (потерям в ме-

ди);

ст

— тепловой поток, мощность которого равна магнитным потерям в стали сердечника;

Р’

, Р’’

, Р’

ст

— тепловые потоки в ветвях схемы замещения;

— тепловое сопротивление катушки собственному потоку потерь;

х — тепловое сопротивление катушки для потока, идущего от максимально нагретой области

до гильзы, величина которого зависит от проходящего через него потока;

— тепловое сопротивление гильзы;

R°

, R°

— тепловые сопротивления граничных слоев: поверхность катушки — среда и поверх-

ность сердечника — среда соответственно.

Так как на практике тепловые сопротивления сердечника собственному и проходящему тепло-

вым потокам значительно меньше R°

, то они в расчете не учитываются.

Когда максимально нагретая область трансформатора находится внутри катушки — наиболее

часто встречающийся случай (рис. 28, а) — тепловой поток (Р

), создаваемый катушкой, распадает-

ся на две составляющие и проходит в окружающую среду по двум путям: одна составляющая (Р

—

Р’

) идет только через часть катушки, преодолевая сопротивления R

— х и R°

, другая состав-

ляющая (Р'

,) проходит через другую часть катушки, гильзу, далее через сердечник и преодолевает

при этом сопротивления х, R

и R°

40. Определяем по табл. 15 и 16 для выбранного магнитопровода тепловые сопротивления

элементов схемы замещения R

, R

, R°

и R°

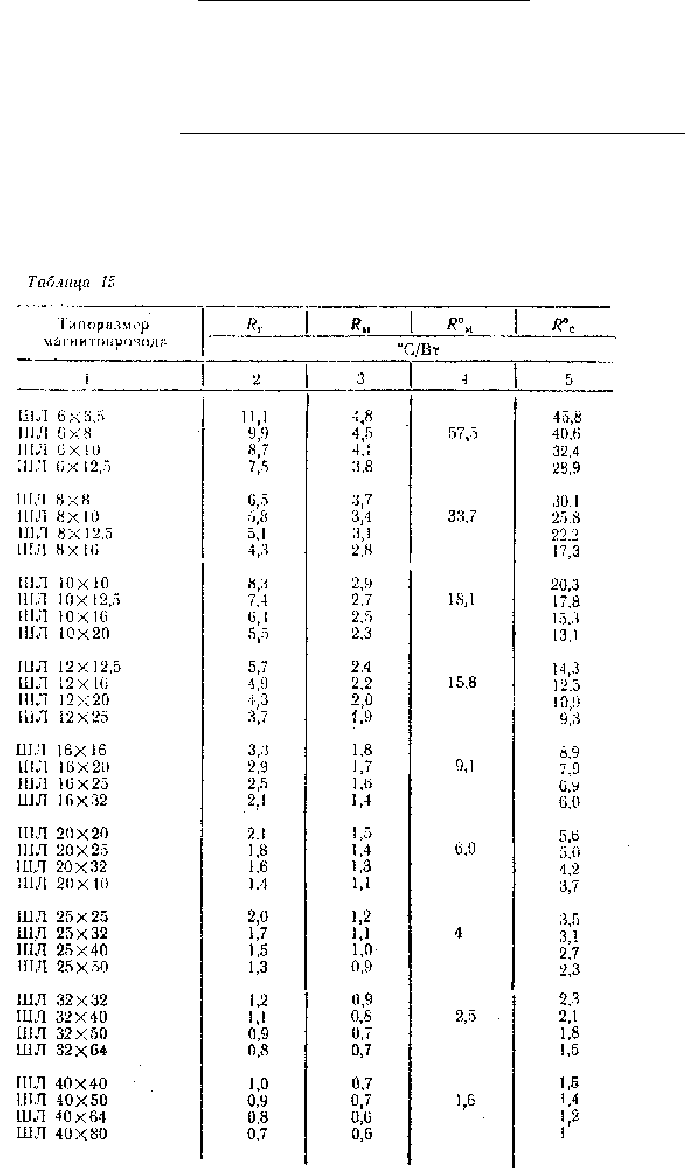
41. Определяем величину теплового потока между катушкой и сердечником

RRRRPRР

RRRR

ммc Гм c ст

ммc Г

()

+°+°

−

+°+°+2

Вт, (48)

где Р

— потери в меди, Вт; Р

ст

— потери в стали, Вт.

42. Определяем тепловое сопротивление катушки от максимально нагретой области до

гильзы (каркаса) по формуле:

PR R R R RР PR R

мм м c Г c ст м м м

+°

−

°'( ) ( )

°С/Вт. (49)

43. Определяем максимальное превышение температуры катушки и среднее превышение

температуры обмотки.

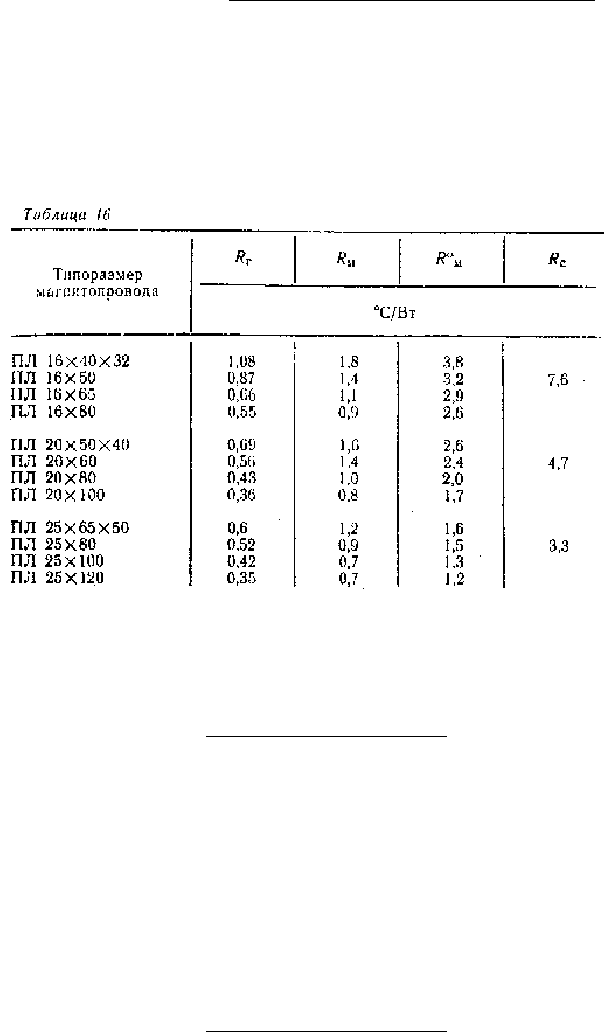
А. Если 0<x<R

(максимально нагретая область находится внутри катушки), то максимальное

превышение температуры катушки следует определять по формуле:

Δθ

макс

мм м c Г c ст

мм м c Г

PR R R R R Р

Р RRRR

+°+°+ +°

+°+°+

[( ) ]

()

°С, (50)

а среднее объемное превышение температуры обмотки по формуле

Δθ Δθ Δθ

смакср

,=−

(51)

где

Δθ Δθ

05 025=

−,,(')

кммм

РРR . (52)

В формулах (51) и (52)

Δθ

— перепад температуры в обмотке, первой намотанной на каркас,

Δθ

— общий перепад температуры в катушке; Р'

определяется из формулы (48).

Б. Если полученное значение х окажется меньше или равным нулю, т. е. тепловой поток направ-

лен от сердечника к катушке и максимально нагретая область находится на гильзе (каркасе), то в

этом случае необходимо определить тепловой поток катушка — сердечник по формуле

PR R R Р

RRRR

мм м c ст

ммc Г

()

+°

+°+°+

Вт. (53)

Если получится Р’’

>0, то максимальное превышение температуры катушки определяют по

формуле

Δθ

макс

= (Р

- Р’’

)(R

+ R°

), (54)

а среднее превышение температуры катушки по формуле

Δθ

ср

= Δθ

макс

- Δθ

, (55)

где Δθ

= (Р

- Р’’

. (56)

В формулах (55) и (56) Δθ

— перепад температуры в катушке.

Если найденное из уравнения (53) значение Р’’

будет меньше нуля, то доля теплового потока,

возникающего в сердечнике, которая будет излучаться в окружающую среду через катушку (рис.

25, в), может быть определена по формуле

PR R R Р

RRRR

ст

мм м c ст

ммc Г

()

+°

+°+°+

Вт. (57)

Максимальное превышение температуры катушки в этом случае определяется по формуле

Δθ

макс

= (Р

ст

- Р’

ст

)R°

, °С, (58)

а среднее -- по формулам (55) и (56).

Для частот 50 и 400 Гц можно с достаточной точностью указать положение максимально нагре-

той области катушки и соответственно рекомендовать использование расчетных

формул для вычисления максимального превышения температуры.

Для трансформаторов с превышением температуры не более +70°С, питающихся от сети 50 Гц, а

также для трансформаторов малых типоразмеров без радиаторов, питающихся от сети частотой 400

Гц, максимально нагретая область находится внутри катушки (0<x<<R

) и поэтому расчеты

можно вести по формуле (50).

Для трансформаторов, питающихся от сети с частотой 400 Гц, при типоразмерах сердечников,

соответствующих ШЛ10 и более, максимально нагретая область находится на гильзе (х<0), и по-

этому расчеты следует вести по формуле (54) .

Для выполнения теплового расчета трансформаторов с любыми соотношениями геометрических

размеров сердечника по описанному

выше методу необходимо определить тепловые сопротивления

, R°

, R

и R

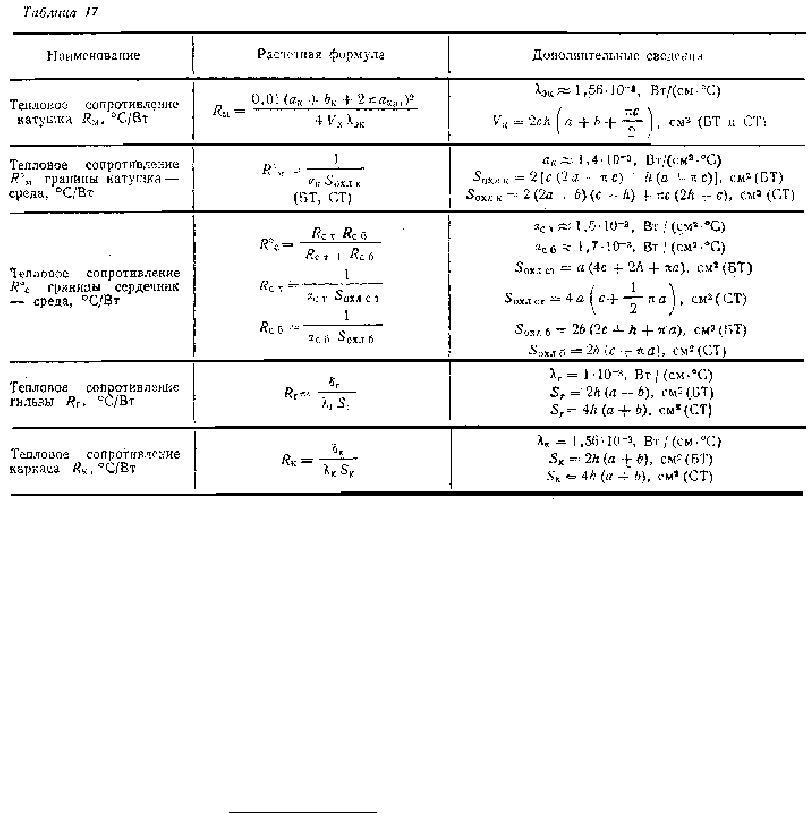
схемы замещения по формулам, приведенным в табл. 17.

Расчетные формулы для определения: объема катушки открытой поверхности охлаждения катушки,

непосредственно участвующей в теплообмене с окружающей средой S

охл к

; открытой торцевой

поверхности сердечника S

охл ст

и его боковой поверхности S

охл б

; поверхности гильзы S

, для

трансформаторов броневой (БТ) и стержневой конструкций (СТ) — приведены в этой же таблице. В

ней также приведены средние значения эквивалентной теплопроводности пропитанной катушки λ

эк

и гильзы λ

и коэффициентов теплоотдачи; с поверхности катушки α

, с торца сердечника α

ст

, с

боковой поверхности сердечника α

сб

В таблице обозначены R

cт

и R

cб

— тепловые сопротивления торцевой и боковой поверхности

сердечника; δ

— толщина гильзы; λ

— теплопроводность гильзы.

Дальнейший тепловой расчет ведут в соответствии с пп. 41 — 43.

44. Оценка результатов расчета перегрева. Во избежание грубых ошибок при расчете макси-

мальной температуры перегрева θ

макс

ее приближенное значение определяют по упрощенной фор-

муле

Δθ Δθ

макс

мс

обм се д

РР

α()

°С, (59)

где Р

— суммарные потери в меди обмоток, Вт;

— суммарные потери в стали сердечника, Вт;