Гладких Б.А. Информатика от абака до интернета. Введение в специальность

Подождите немного. Документ загружается.

§ 1.3] ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА И ЕЕ ПОТОМКИ 31

Нас, однако, будут интересовать сейчас не конкретные приемы ра-

боты с логарифмической линейкой, а более общий вопрос о взаимо-

отношении дискретного и непрерывного

в вычислительной технике.

На абаке или счетах число представ-

ляется в цифровой, т.е. в символической,

знаковой форме, и это представление

совершенно точное. Если 375 так 375, не

больше и не меньше. Каждый разряд

числа изображается целым числом ка-

мешков, нельзя положить 3 с половиной

или 5 и 6 десятых камня. Даже если чис-

ло не целое, то точно представляется

соответствующая ему десятичная дробь с фиксированным числом зна-

ков после запятой. Поэтому абак является простейшим примером циф-

ровой или, более точно, дискретной вычислительной машины (так как

представляться могут не только числа, но и другие дискретные объекты

– тексты, оцифрованные образы и др).

В противоположность абаку, на логарифмической линейке пред-

ставляется не цифровая запись числа, а некоторый его физический ана-

лог. Первому сомножителю соответствует перемещение движка отно-

сительно неподвижной шкалы, второму – перемещение визира бегунка

относительно шкалы движка, результату – перемещение бегунка отно-

сительно неподвижной шкалы. Аналоги являются непрерывными физи-

ческими величинами, поэтому представление всегда не точное, а при-

ближенное, так как невозможно точно выставить движок на цифру,

скажем, 2, будет или меньше или больше, да и сами шкалы имеют неко-

торую погрешность. Таким образом, логарифмическая линейка является

простейшим примером аналоговой вычислительной машины (АВМ).

Цифровые (дискретные) и аналоговые вычисления – это две посто-

янно сосуществующие и конкурирующие ветви математики. Математи-

ка Древнего мира была в подавляющей степени связана с аналоговыми

(геометрическими) построениями. Строго говоря, циркуль и линейка –

это тоже древнейшая аналоговая вычислительная машина.

С изобретением символических алгоритмов арифметики роль ана-

логовых вычислений стала ослабевать, так как цифровые методы спо-

собны обеспечить более высокую точность вычислений. Обычная лога-

рифмическая линейка дает результат с точностью до 1–0.1% (2–3 зна-

ков после запятой), причем ошибка быстро накапливается с увеличени-

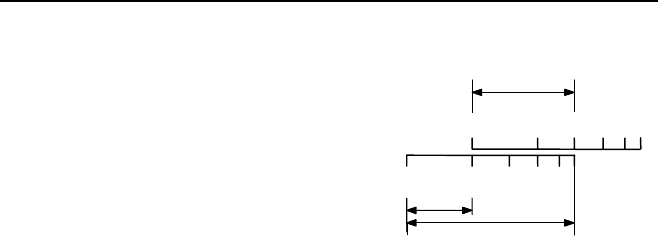
1 2 3 4 5 6

a • b

Принцип действия

логарифмической линейки

a = 2, b = 3, a

• b = 6

32 ДОЭЛЕКТРОННАЯ ИСТОРИЯ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ [ГЛАВА 1

ем сложности вычислений. Для астрономии или географии такая точ-

ность совершенно недостаточна, поэтому, начиная с XVII века, конст-

рукторская мысль была направлена в основном на создание и развитие

цифровых вычислительных машин, и что из этого получилось – мы

увидим дальше.

Однако не всегда и не везде нужна астрономическая точность, по-

этому, параллельно с цифровой, развивалась и аналоговая вычисли-

тельная техника. В XIX и XX ве-

ках для аналоговых вычислений

использовались самые различные

физические процессы: механиче-

ские, гидравлические. Например, в

1930 году профессор Массачусетс-

ского технологического института

(МТИ) Ванневар Буш (Bush,

Vannevar; 1890–1974) построил

«дифференциальный анализатор»

– большую механическую анало-

говую машину, способную решать

сложные дифференциальные урав-

нения. Он представлял собой

сложнейшую систему реек, шесте-

ренок, валиков занимавшую целый

зал. Обязанности оператора на этой машине выполнял молодой аспи-

рант Клод Шеннон – будущий автор теории информации. С тех пор

МТИ превратился в крупнейший центр исследований в области вычис-

лительной техники и информатики

, а Буш, ставший в годы Второй ми-

ровой войны советником президента США по науке, сыграл важную

роль в развитии современных информационных систем (подробнее об

этом мы будем говорить в главе 4).

После изобретения радиоламп и транзисторов в середине XX века

появились электронные АВМ, которые завоевали к 1960-х годам боль-

шую популярность, сравнимую с популярностью цифровых вычисли-

Город Бостон, штат Массачусетс, благодаря своему пригороду Кембриджу издав-

на считается интеллектуальной столицей Восточного побережья США. Здесь в

XVII веке был основан старейший и престижнейший Гарвардский университет,

носящий имя его основателя Джона Гарварда. Расположенный в том же Кембридже

Массачусетсский технологический институт был основан значительно позже – в

1861 году.

Дифференциальный анализатор

Ванневара Буша (1930 г.)

§ 1.3] ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА И ЕЕ ПОТОМКИ 33

тельных машин (ЦВМ), их изучение было обязательным на всех техни-

ческих факультетах. Это объяснялось многими факторами:

• аналоговые машины в то время были намного проще, меньше

по размерам и дешевле цифровых;

• на аналоговых машинах очень легко выполнялись трудоемкие

операции дифференцирования и интегрирования функций, ре-

шения дифференциальных уравнений высоких порядков;

• результат вычислений получался немедленно после ввода ис-

ходных данных, причем этот результат выводился в виде физи-

ческой величины и мог быть непосредственно использован для

отображения на экране осциллографа (графических дисплеев не

было еще и в помине).

В силу указанных причин аналоговые вычислительные машины

широко использовались в системах управления самолетами, ракетами,

производственными процессами.

Однако после изобретения микропроцессоров (1970-е годы), когда

ЦВМ резко уменьшились в габаритах и подешевели, аналоговые ЭВМ

сильно сдали в конкурент-

ной борьбе с ними. Стало

проще перевести аналого-

вый сигнал в цифровую

форму, выполнить требуе-

мые вычисления, а на выхо-

де обратно преобразовать

результат в физическую

величину. По такому пути

пошли звукозапись и теле-

видение – об этом мы также

поговорим позже.

Значит ли это, что ана-

логовые вычисления вытес-

нены навсегда? Я глубоко

убежден, что нет, и в этом одно из проявлений цикличности техниче-

ского прогресса. Дело в том, что некоторые объекты, например графи-

ческие или звуковые образы, являются исключительно трудными для

символьной обработки. Например, самые мощные цифровые процессо-

ры, вооруженные наисовременнейшими алгоритмами, с большим тру-

дом и недостаточным пока качеством справляются с задачами чтения

слитного рукописного текста или распознаванием потока речи, а чело-

Большая электронная аналоговая

вычислительная машина (1950-е годы)

34 ДОЭЛЕКТРОННАЯ ИСТОРИЯ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ [ГЛАВА 1

век решает эти задачи относительно легко. Почему? Установлено, что в

человеческом мозгу одно полушарие (левое), подобно цифровой вычис-

лительной машине, оперирует со знаками и абстрактными понятиями.

Правое же полушарие отвечает за образное, неструктурированное, ана-

логовое мышление. Только совместная работа обоих полушарий делает

мозг таким, как он есть – пока недоступным для конкуренции со сторо-

ны чисто цифровых компьютеров.

Попытки «впрячь в одну телегу коня и трепетную лань» приводят к

идее построения гибридных, то есть цифро-аналоговых вычислительных

машин, которые представляются весьма перспективными для XXI века.

Мы остановились на аналоговых вычислительных машинах для то-

го, чтобы к этой теме больше не возвращаться. Все дальнейшее изло-

жение будет посвящено проблемам цифровых машин – их прошлому,

настоящему и будущему.

Вернемся же в славный XVII век и познакомимся с историей созда-

ния первой механической цифровой вычислительной машины.

§ 1.4. Суммирующая машина Паскаля

Честь создания первой механической счетной машины принадлежит

великому французскому ученому и изобретателю Блезу Паскалю

(Pascal, Blaise; 1623–1662), известному своими

достижениями в физике и математике (закон

Паскаля для жидкостей и газов, треугольник

Паскаля для вычисления биномиальных коэф-

фициентов и др.)

Отец Паскаля, который во времена карди-

нала Ришелье (Richelieu; 1585–1642) служил

сборщиком налогов, очень много времени и

сил тратил на утомительные арифметические

выкладки, и юный Блез задался целью облег-

чить арифметические вычисления для отца. В

1642 году, в возрасте 19 лет, он публично про-

демонстрировал механическую вычислитель-

ную машину – «Паскалину».

В современных исследованиях по истории вычислительной техники приоритет

Паскаля подвергается сомнению (см. «Комментарии…» в конце книги).

Блез Паскаль

(1623–1662)

§ 1.4] СУММИРУЮЩАЯ МАШИНА ПАСКАЛЯ 35

Главный недостаток абака или

счетов – необходимость ручного пе-

реноса единицы в старший разряд при

переполнении предыдущего. Механи-

зировать этот процесс на камешках

(костяшках) не удавалось, нужно было

изобрести новый элемент с десятью

устойчивыми состояниями, отобра-

жающими цифры разряда. После дол-

гих раздумий Паскаль изобрел ... ко-

лесо, но не простое, а зубчатое, с 10 зубцами. Поворот колеса на один

зубец (1/10 часть окружности) соответствует увеличению значения раз-

ряда на единицу, а при полном обороте колеса специальный, довольно

сложный, механизм передачи десят-

ков (см. рис.) поворачивает следую-

щее колесо ровно на один зубец.

Говоря современным языком,

Паскаль изобрел многоразрядный

десятичный механический счетчик

оборотов, который до сих пор ис-

пользуется в спидометрах автомоби-

лей, электросчетчиках и т.д. Более

того, счетчик Паскаля с некоторыми

усовершенствованиями стал цен-

тральным устройством – суммато-

ром – всех последующих механиче-

ских и электромеханических вычис-

лительных машин вплоть до середи-

ны XX века, и даже в первых конст-

рукциях электронных машин сред-

ствами электроники моделировалась

работа циклического десятичного счетчика, пока фон Нейман не пред-

ложил перейти на двоичную систему счисления (об этом мы будем го-

ворить в следующей главе).

Паскаль более 10 лет занимался усовершенствованием своей маши-

ны, было сделано 50 ее экземпляров из латуни, слоновой кости, других

материалов (до наших дней сохранилось восемь, в том числе один хра-

нится в музее корпорации IBM). Машина получила известность, а Пас-

каля за ее изобретение сравнивали с Архимедом. Множество людей

Паскалина (1642 г.)

Механизм передачи десятков

в машине Паскаля

36 ДОЭЛЕКТРОННАЯ ИСТОРИЯ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ [ГЛАВА 1

приходило в Люксембургский дворец, где она была выставлена для все-

общего обозрения. Однако широкого распространения Паскалина не

получила по нескольким причинам. Во-первых, она была достаточно

сложной и дорогой, а во-вторых, и это самое главное, машина предна-

значалась исключительно для сложения и вычитания 6–10-разрядных

чисел, а самые трудоемкие операции умножения и деления она не ме-

ханизировала. Этого удобства сборщикам налогов пришлось ждать еще

30 лет.

§ 1.5. Арифмометр – от машины Лейбница до

электронного калькулятора

Операция умножения многозначных чисел сводится к повторному

сложению; именно так поступаем мы, выполняя умножение «столби-

ком» на бумаге (см. пример).

При реализации этого алгоритма на машине Паскаля приходится не-

сколько раз (в нашем примере шесть) вводить одно и то же множимое,

временами сдвигая его на один разряд влево, что очень утомительно.

Оригинальное решение проблемы предложил в 1673 году знамени-

тый немецкий математик, философ, дипломат Готфрид Лейбниц

1526 1526

312

1526 1526

1526 3052

1526 сдвиг-> 3052

1526 1526

1526

18312

476112 сдвиг-> 18312

1526

476112

а) б)

Алгоритм умножения целых чисел при вычислениях

на бумаге и машине Паскаля (а) и на арифмометре (б)

§ 1.5] АРИФМОМЕТР – ОТ МАШИНЫ ЛЕЙБНИЦА ДО ЭЛЕКТРОННОГО КАЛЬКУЛЯТОРА 37

(Leibnitz, Gottfried; 1646–1716). Он ввел в вычислительную машину два

принципиальных усовершенствования.

Во-первых, для повторного ввода одного и

того же числа он использовал ступенчатые ва-

лики (по одному на каждый разряд) и поворот-

ную рукоятку. Поворачивая рукоятку на один

оборот, можно, в зависимости от положения

промежуточной шестеренки на валике, добить-

ся ее поворота на заданную долю окружности.

Во-вторых, он поместил механизм ввода

чисел на подвижную каретку, которая на оче-

редном шаге умножения перемещается влево

относительно суммато-

ра на один разряд (в

последующих конст-

рукциях арифмометров

оказалось удобнее неподвижным сделать меха-

низм ввода, а на каретку поместить сумматор,

поэтому сдвиг сумматора происходит вправо).

Таким образом, введя один раз множимое,

можно многократно вводить его со сдвигом в

счетчик, производя операцию умножения. Опе-

рация деления выполняется аналогично, путем

повторного вычитания делителя из делимого,

для чего рукоятку прибора следует крутить в

другую сторону.

Арифметическая машина Лейбница совер-

шенствовалась в деталях, но не в принципе, на протяжении следующего

XVIII, а затем и XIX века, она

получила название арифмомет-

ра и стала производиться мно-

гими фирмами. Наиболее попу-

лярной была модель француз-

ского инженера Карла Томаса,

который в 1821 году организо-

вал серийное производство

арифмометров в Париже, поэтому арифмометры этой конструкции на-

зывались томас-машинами.

Готфрид Лейбниц

(1646–1716)

Ступенчатый валик

Лейбница

Арифмометр Лейбница (1673 г.)

38 ДОЭЛЕКТРОННАЯ ИСТОРИЯ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ [ГЛАВА 1

Только через 200 лет, в 1873 году петербургский изобретатель

В.Т. Однер, швед по происхождению, предложил более простое и ком-

пактное, чем валик Лейбница, устройство для ввода чисел в арифмо-

метр – так называемое колесо Однера с переменным числом зубцов. На

базе своего изобретения Однер организовал широкомасштабное произ-

водство арифмометров. В 1917 году Однер эмигрировал в Швецию, но

производство арифмометров в России постоянно увеличивалось. На

московском заводе имени Ф. Дзержинского арифмометры Однера вы-

пускались под маркой «Феликс», в 1969 году их было произведено

300

000 шт.

С помощью арифмометра были составле-

ны фундаментальные математические табли-

цы, выполнены сложнейшие астрономические

расчеты, так что «железный Феликс» – это

почтенный и заслуженный вычислительный

прибор, и в коллекции музея истории вычис-

лительной техники он стоит на самом почет-

ном месте.

Усовершенствование арифмометра про-

должалось вплоть до 70-х годов XX века. К

ручке приделали электромоторчик, неудобный рычажковый ввод заме-

нили на клавишный – в результате появилось целое семейство электро-

механических калькуляторов.

Я застал эти машины в лаборатории

счетно-решающих устройств Томского

университета в середине 1960-х годов.

Особенное впечатление произвела не-

мецкая Zoemtron тем, что она совершен-

но самостоятельно, с ужасающим трес-

ком и лязганьем производила деление

многозначных чисел. Любимым заняти-

ем было заставить ее делить на нуль и

посмотреть, что из этого получится. Ма-

шина не замечала подвоха и продолжала

греметь шестеренками до тех пор, пока

нажатием специальной клавиши не оста-

навливали это пустое занятие.

В середине 1960-х годов появились первые электронные калькуля-

торы. По своим функциональным возможностям они полностью копи-

Арифмометр "Феликс-М",

выпуск 1960-х годов

Электромеханический

калькулятор

середины 1960-х годов

§ 1.6] ПРИНЦИП ПРОГРАММНОГО УПРАВЛЕНИЯ 39

ровали электромеханические вычислители, имели приблизительно те

же размеры, зато работали бесшумно. За прошедшие 30 лет калькулято-

ры сильно «похудели» (сейчас их встраи-

вают даже в часы и авторучки), подеше-

вели, стали удобнее в пользовании и

проч. и проч. Однако в идейном отноше-

нии современные электронные калькуля-

торы недалеко ушли от арифмометра

Лейбница: они предназначены для вы-

полнения одной изолированной опера-

ции. Если нужно выполнить цепочку вы-

числений, то приходится каждый раз за-

писывать результат на бумажку и вновь

вручную вводить исходные данные для

следующей операции. И никакая элек-

троника сама по себе ничего нового не дает, так как в калькуляторах

(механических или электронных) не реализован фундаментальный

принцип, который собственно и превратил калькулятор в компьютер –

принцип программного управления.

§ 1.6. Принцип программного управления.

Вычислительные машины Бэббиджа

С точки зрения вычислительной техники XVIII век

был беден крупными событиями, но вот наступил

век XIX. Великая французская революция, европей-

ские войны, звездный час наполеоновской империи...

На фоне этих политических событий было сделано одно эпохальное

техническое изобретение: в 1801 году французский механик Жаккар

(Jacquard, Joseph-Marie; 1752–1834) построил ткацкий станок, который

автоматически, без участия человека, ткал узорное полотно (оно так

теперь и называется – жаккардовое). Станок управлялся программным

механизмом на перфокартах.

Перфокарта представляла собой прямоугольный кусок тонкого кар-

тона с пробитыми на нем рядами отверстий, каждый ряд соответствовал

одной нити основы ткани. Желаемый рисунок предварительно кодиро-

вался на перфокартах, в процессе работы цепочка перфокарт протяги-

валась через станок и ощупывалась программным механизмом. Есть

Электронный калькулятор

(1970-е годы)

Программное

управление

40 ДОЭЛЕКТРОННАЯ ИСТОРИЯ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ [ГЛАВА 1

отверстие – щуп опускался, и

челнок в этом месте нырял под

основу, нет – челнок проходил

над основой. Таким образом

можно запрограммировать сколь

угодно сложный рисунок, и ста-

нок отрабатывал его без ошибок

и с недостижимой для человека

скоростью. Более того, для того

чтобы сменить рисунок, не нуж-

но переналаживать станок – дос-

таточно просто сменить про-

грамму на перфокартах. В усо-

вершенствованных станках мож-

но было программировать даже

циклы для повторяющихся час-

тей рисунков.

Станок Жаккара произвел революцию в технике, ибо он ознамено-

вал собой воплощение нового технологического принципа – принципа

программного управления. Вслед за ткацким станком вскоре появились

и другие программно-управляемые автоматы, например механическое

пианино – пианола.

Идея применить принцип про-

граммного управления к вы-

числительному устройству и

«ткать алгебраические узоры, как ткацкий

станок Жаккара – цветы и листья»

была вы-

сказана выдающимся английским ученым и

изобретателем Чарльзом Бэббиджем

(Babbage, Charles; 1791–1871).

Судьба Бэббиджа замечательна и драма-

тична. Сын богатых родителей, выпускник

Кембриджского университета, он отличался

чрезвычайно широкими научными интереса-

ми и до глубокой старости сохранял высокую

работоспособность. Опубликовал множество

Это сравнение принадлежит Аде Лавлейс.

Ткацкий станок Ж. Жаккара

(1801 г.)

Чарльз

Бэббидж

Чарльз Бэббидж

(1791–1871)