Ghasem D. Najafpour. Biochemical Engineering and Biotechnology

Подождите немного. Документ загружается.

Equation 5.7.1.34 gives:

(5.7.1.36)

Equation 5.7.1.32 leads to:

(5.7.1.37)

The free enzyme concentration is:

(5.7.1.38)

Substituting (5.7.1.38) into (5.7.1.36) results in:

(5.7.1.39)

The intermediate complex ES is defined:

(5.7.1.40)

The enzyme rate equation with two dissociation relations at equilibrium yields:

(5.7.1.41)

Now, maximise the rate at a specific substrate concentration:

(5.7.1.42)

Maximum substrate concentration is defined by the square root of the dissociation constants

(5.7.1.43)

At a high substrate concentration, the rate can be simplified and a linearised model is obtained:

(5.7.1.44)

⫽⫹

[]S

SKK

max

⫽

⫽⫽⫺ ⫹ ⫽0



y ⫽⫹⫹ke

[]

ES K e S K

⫽⫹⫺

Ke K

KES

KES ESS

o22

⫺⫺⫽

[]

[][][]

[]

KES

⫽

KES ES

[][][]⫽

Ke KE K ES ES S

o222

⫺⫺ ⫽[][][]

104 BIOCHEMICAL ENGINEERING AND BIOTECHNOLOGY

Ch005.qxd 10/27/2006 10:44 AM Page 104

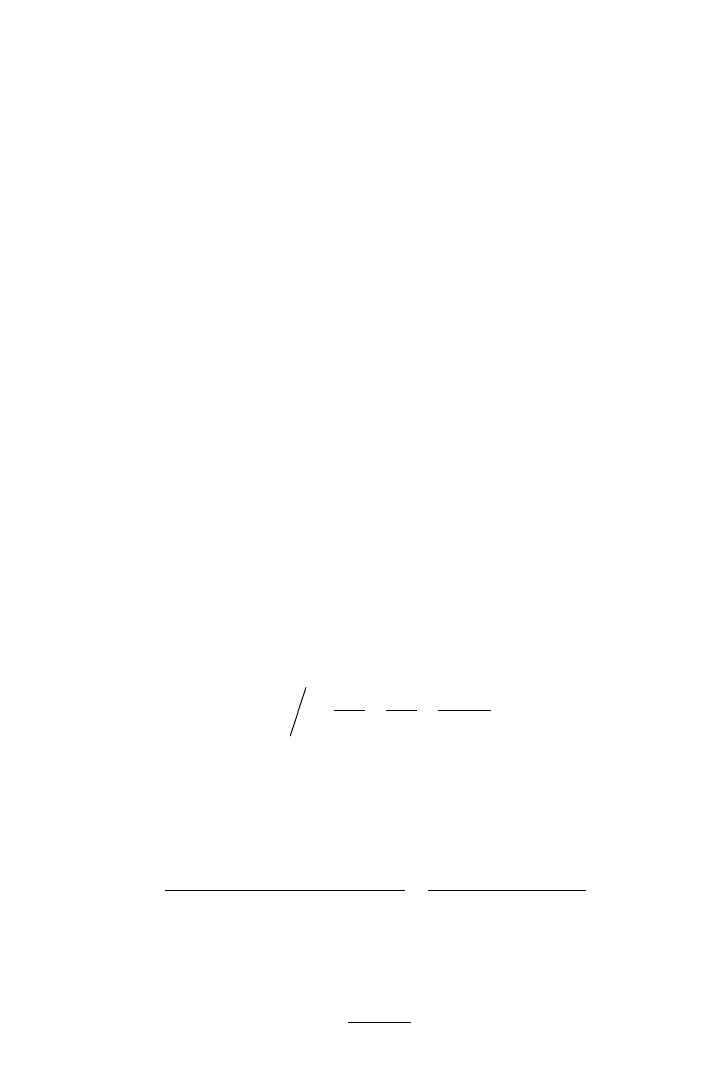
A graph of 1/y versus S is plotted and the slope is 1/K

. There is an intercept in the

graphical presentation to identify another constant. From the above equation, K

can be cal-

culated, which is similar to S

max

, where S

max

means that the substrate concentration gives

the maximum rate.

5.7.2 Kinetics of Reversible Reactions with Dual Substrate Reaction

The reaction mechanisms for reversible reactions are slightly different. In the above sec-

tion, the second part of the reaction that leads to product was irreversible. However, if all

the steps in enzyme reactions were reversible, the resulting rates may be affected.

(5.7.2.1)

where k

is the rate constant for forward and k

⫺1

the rate constant for backward reactions.

The second reaction is:

(5.7.2.2)

where k

is the rate constant for forward and k

⫺2

the rate constant for backward reactions.

For dual substrates the reaction mechanisms may be complicated if the enzyme–substrate

complex of the first substrate reacts with the second substrate; then the dissociation con-

stant of K

is defined to present the equilibrium, and vice versa the dissociation constant

for the reaction of second substrate–enzyme complex with the first substrate is K

(5.7.2.3)

The rate equation for reversible reactions with two substrates is defined.

(5.7.2.4)

Assume

(5.7.2.5)

(5.7.2.6)

For the special case the rates are simplified to more familiar rates and result in the following:

(5.7.2.7)

⫽

⫹

max

y ⫽

⫹⫹⫹

⫽

⫹⫹

ke S S

SS KS KS KK

ke S S

KSKS

oo21

12 212 121 2 21

12 2 1 1

()()

KK KK

112 2 21

y ⫽ ⫹⫹⫹ke

221

e e ES ES ES S

⫽⫹ ⫹ ⫹

1212

ES P E ⫹

SE ES

⫹

⫺

¨Æææ

GROWTH KINETICS 105

Ch005.qxd 10/27/2006 10:44 AM Page 105

where y

max

and K

are the apparent maximum rate and Michaelis constant, respectively.

(5.7.2.8)

(5.7.2.9)

If one substrate is in great excess, K

is small or S

⬎⬎ K

then y

max

⫽ ke

and K

⬵K

. In

this case we can simplify the rate to:

(5.7.2.10)

5.7.3 Reaction Mechanism with Competitive Inhibition

Generally inhibitors are competitive or non-competitive with substrates. In competitive

inhibition, the interaction of the enzyme with the substrate and competitive inhibitor

instead of the substrate can be analysed with the sequence of reactions taking place; as a

result, a complex of the enzyme–inhibitor (EI) is formed. The reaction sets at equilibrium

and the final step shows the product is formed. The enzyme must get free, but the enzyme

attached to the inhibitor does not have any chance to dissociate from the EI complex. The

EI formed is not available for conversion of substrate; free enzymes are responsible for that

conversion. The presence of inhibitor can cause the reaction rate to be slower than the ordi-

nary reaction, in the absence of the inhibitor. The sequence of reaction mechanisms is:

(5.7.3.1)

(5.7.3.2)

where K

and K

are dissociations for the Michaelis–Menten rate constant and the inhibi-

tion constant, respectively:

(5.7.3.3)

The total enzyme concentration is the sum of all enzymes as free, and those conjugated as

ES and EI:

(5.7.3.4)

e E ES EI

⫽⫹ ⫹

ES E P

æÆæ ⫹

EI EIK

⫹  ,

ES ESK

⫹  ,

y ⫽

⫹

ke S

o 1

21 1

KK K S

112 122

12 2

⫽

⫹

max

⫽

⫹

ke S

o 2

12 2

106 BIOCHEMICAL ENGINEERING AND BIOTECHNOLOGY

Ch005.qxd 10/27/2006 10:44 AM Page 106

The reaction rate model is based on total enzyme, substrate and inhibitor concentrations.

(5.7.3.5)

Comparison of the ordinary Michaelis–Menten relation with (5.108) shows that the inhibitor

did not influence specific growth rate, y

max

, but the Michaelis–Menten constant was affected

by the inhibitor and resulted in a constant, known as the apparent Michaelis constant.

(5.7.3.6)

where K

app

is apparent Michaelis constant. The rate constant is increased by the presence

of a competitive inhibitor. The inhibitor causes the reaction rate to slow down. The compet-

itive inhibitor can be unaffected or eliminated by increasing the substrate concentration.

5.7.4 Non-competitive Inhibition Rate Model

The non-competitive inhibitor is defined by the following sequence of reactions:

(5.7.4.1)

(5.7.4.2)

In such inhibition, the inhibitor and the substrate can simultaneously bind to the enzyme.

The nature of the enzyme–inhibitor–substrate binding has resulted in a ternary complex

defined as EIS. The K

and K

are identical to the corresponding dissociation constants. It

is also assumed that the EIS does not react further and is unable to deliver any product P.

The rate equation for non-competitive inhibition, u

max

, is influenced:

(5.7.4.3)

The maximum specific growth rate is retarded with non-competitive inhibitor. The appar-

ent specific growth rate, y

app

max

, is smaller than the ordinary specific growth rate, y

max

(5.7.4.4)

max

app

⫽

⫹

y ⫽

⫹

ke S

ES I ESI K

⫹  ,

EI S EIS K

⫹  ,

app

⫽⫹1

y ⫽

⫹⫹

ke S

GROWTH KINETICS 107

Ch005.qxd 10/27/2006 10:44 AM Page 107

If the complex of ESI can be dissociated to product, the rate equation would result in mixed

competitive and non-competitive inhibitors:

(5.7.4.5)

(5.7.4.6)

The competitive and non-competitive inhibitors are easily distinguished in a Lineweaver–

Burk plot. The competitive inhibitor intercepts on the 1/y axis whereas the non-competitive

inhibitor intercepts on the 1/S axis. The reaction of inhibitors with substrate can be assumed

as a parallel reaction while the undesired product is formed along with desired product. The

reactions are shown as:

(5.7.4.7)

(5.7.4.8)

Since enzyme is not shown in the reaction we assume an elementary rate equation may

explain the above reactions. The simple kinetics are discussed in most fermentation tech-

nology and chemical reaction engineering textbooks.

8–10

Example 1

An enzyme is produced for manufacturing a sun protection lotion. Given kinetic data for

the enzyme reaction with , Km ⫽ 8.9 mM and S

⫽ 12 mM, what would be

the time required for 95% conversion in a batch bioreactor?

Solution

Example 2

Calculate K

and V

max

for given substrate concentrations and rates. The inverse rate and

substrate concentrations are calculated in Table E.2.1.

batch

mM/h

h⫽⫹⫽

095 12

423

(. )( )

max

.⫽⫽25

3600 1

1000

mmol

max

.⫽ 25

mmol

æÆæ undesired

æÆæ desired

⫽

⫹

max

app

EIS EI P

æÆæ ⫹

108 BIOCHEMICAL ENGINEERING AND BIOTECHNOLOGY

Ch005.qxd 10/27/2006 10:44 AM Page 108

Solution

Let us inverse the substrate concentration and reaction rate as shown in Table E.2.2.

In evaluation of kinetic parameters, the double reciprocal method is used for linearisa-

tion of the Michaelis–Menten equation (5.7.3).

(a) Use the Lineweaver–Burk plot as defined in the following relation:

(E.2.1)

(E.2.2)

⫽⫻

⫺

9.6 10 mol/l

max

.⫽ 0 077

max

1.25 10 mol/l min⫽⫻

⫺

⭈

Slope ⫽

⫺

⫻⫺⫻

⫽

22500 10000

1 875 10 2 5 10

0 077

11 1

yy y

⫽⫹

max max

GROWTH KINETICS 109

TABLE E.2.1. Substrate concentration

and reaction rate

S (mol⭈l

⫺1

) y (mol⭈l

⫺1

⭈min

⫺1

)

4.10 ⫻ 10

⫺3

1.77 ⫻ 10

⫺4

9.50 ⫻ 10

⫺4

1.73 ⫻ 10

⫺4

5.20 ⫻ 10

⫺4

1.25 ⫻ 10

⫺4

1.03 ⫻ 10

⫺4

1.06 ⫻ 10

⫺4

4.90 ⫻ 10

⫺5

8.00 ⫻ 10

⫺5

1.06 ⫻ 10

⫺5

6.70 ⫻ 10

⫺5

5.10 ⫻ 10

⫺6

4.30 ⫻ 10

⫺5

TABLE

E.2.2.

1/S,l⭈mol

⫺1

1/y,l⭈min⭈mol

⫺1

243.9 5650

1052.6 5780

1923.0 8000

9708.7 9434

20408.1 12500

94339.6 14925

196078.4 23256

Ch005.qxd 10/27/2006 10:44 AM Page 109

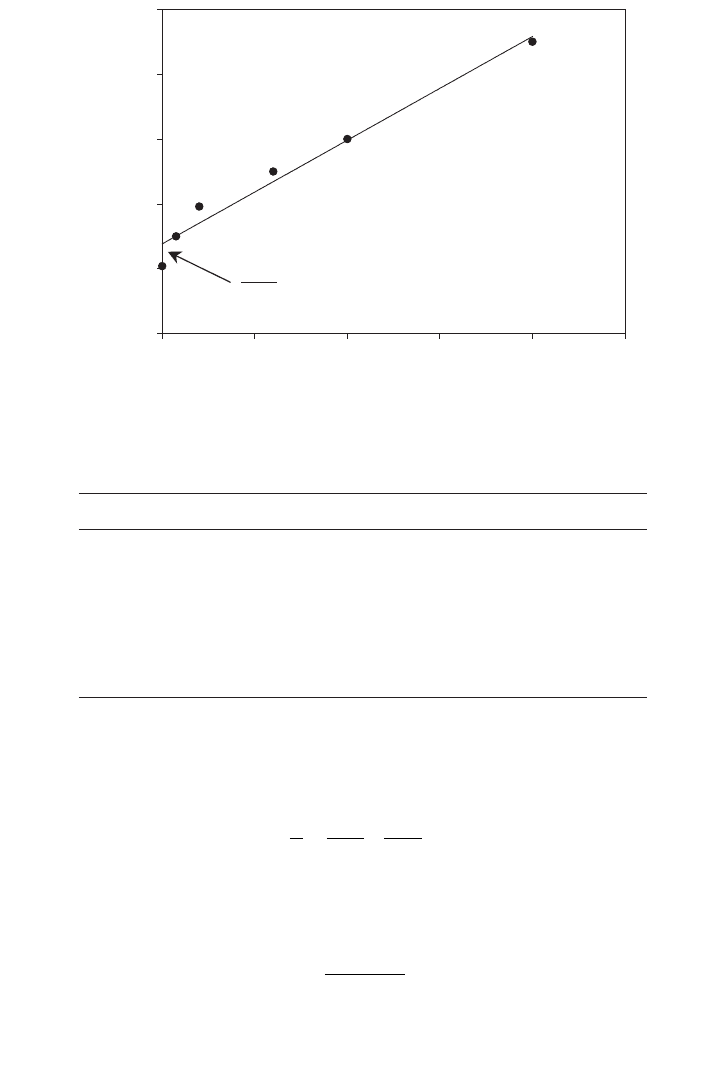
(b) Use another form of linear graphical presentation to evaluate K

and V

max

based on

the following relation:

(E.2.3)

This method tends to create a cluster of data near the origin as shown in Figure E.2.2.

max

.⫽⫻

⫺

182 10

mol/l min⭈

Slope ⫽

⫺

⫻

⫽

⫺

22 5 6 0

310

5500

yy y

⫽⫹

max max

110 BIOCHEMICAL ENGINEERING AND BIOTECHNOLOGY

1/s, l/mol

0.0 5.0e+4 1.0e+5 1.5e+5 2.0e+5 2.5e+5

1/ν, l. min. mol

-1

5000

10000

15000

20000

25000



max

FIG. E.2.1. Lineweaver–Burk plot.

TABLE

E.2.3. Data collected and calculated for rate model

S (mol⭈l

⫺1

) y, mol⭈l

⫺1

⭈min

⫺1

S/y,min y/S,min

⫺1

4.10 ⫻ 10

⫺3

1.77 ⫻ 10

⫺4

23.00 0.044

9.50 ⫻ 10

⫺4

1.73 ⫻ 10

⫺4

5.50 0.182

5.20 ⫻ 10

⫺4

1.25 ⫻ 10

⫺4

4.20 0.240

1.03 ⫻ 10

⫺4

1.06 ⫻ 10

⫺4

0.97 1.030

4.90 ⫻ 10

⫺5

8.00 ⫻ 10

⫺5

0.60 1.670

1.06 ⫻ 10

⫺5

6.70 ⫻ 10

⫺5

0.16 6.250

5.10 ⫻ 10

⫺6

4.30 ⫻ 10

⫺5

0.12 8.330

Ch005.qxd 10/27/2006 10:44 AM Page 110

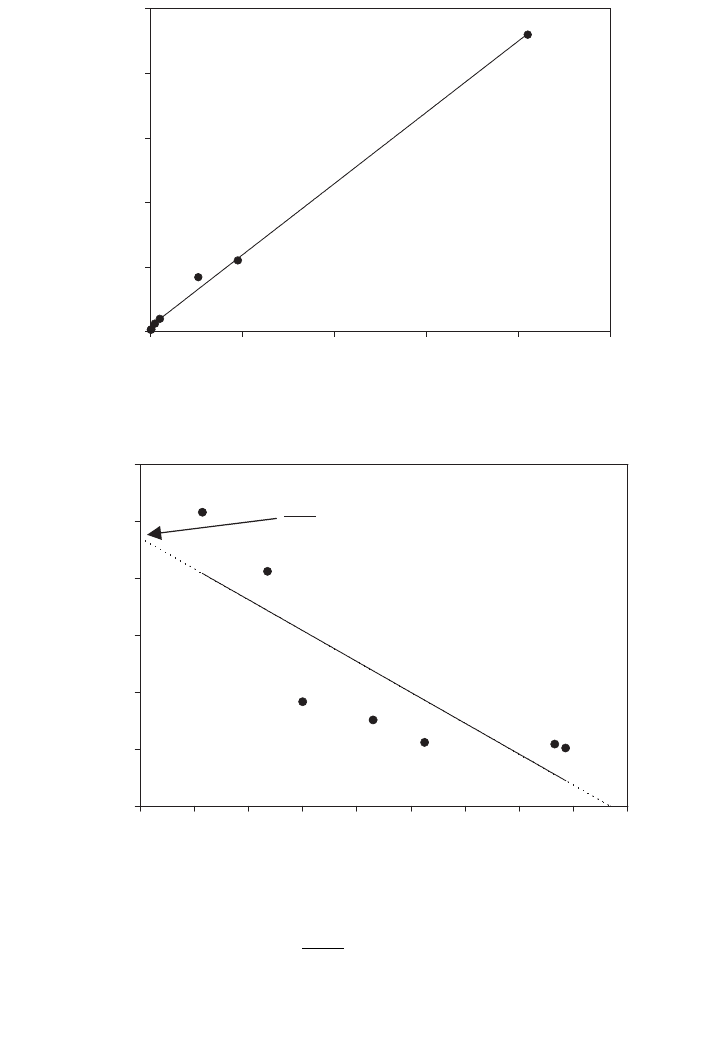
For the Eadie–Hofstee plot, both coordinates contain rates that are subjected to the great-

est error, as indicated in Figure E.2.3.

⫽⫽⫻

⫺

5500

91 10

.mo

GROWTH KINETICS 111

S, mol/l

0.000 0.001 0.002 0.003 0.004 0.005

S/ν, min

FIG. E.2.2. Linear model for the Monod rate equation with populated data at the origin.

ν, mol.l

-1

.min

-1

2e-5 4e-5 6e-5 8e-5 1e-4 1e-4 1e-4 2e-4 2e-4 2e-4

ν/S, min

-1

-2



max

FIG. E.2.3. Eadie–Hofstee plot.

Ch005.qxd 10/27/2006 10:44 AM Page 111

(E.2.3)

A plot of u/S versus y is presented in Figure E.2.3 for defining slope and intercept, K

and

max

, respectively.

A linearisation model is used to explain the equation of a simple straight line:

(E.2.4)

where

(E.2.5)

(E.2.6)

are average values of x

and y

Example 3

In batch enzyme reaction kinetics, given K

⫽ 10

⫺3

M and substrate concentration S

⫽

3 ⫻ 10

⫺5

M, after 2 min, 5% of the substrate was converted. How much of the substrate was

consumed after 10, 20, 30 and 60 min?

Solution

For S

⬍⬍ K

, the rate model is reduced to a first-order rate equation:

The Michaelis–Menten rate equation is:

(E.3.1)

⫽

⫹

max

min⫽⫻

⫺⫺⫺

18 10

411

mol l⭈⭈

⫽⫻

⫺⫺

65 10

. mol l⭈

Slope of the line ⫽

aybx⫽⫺

xy Nxy

xNx

⫽

⫺

ybxa⫽⫹

⫽⫺

max

112 BIOCHEMICAL ENGINEERING AND BIOTECHNOLOGY

xy,

Ch005.qxd 10/27/2006 10:44 AM Page 112

The simplified first-order rate is

(E.3.2)

Carry out integrations:

(E.3.3)

(E.3.4)

The concentration profile is predicted by the following equation

(E.3.5)

At time equal to 2 min:

(E.3.6)

(E.3.7)

(E.3.8)

(E.3.9)

(E.3.10)

⫽⫺

⫽

⫺

ln .

. min

095

0 2565

0 02565

⫺

⫽

.095

⫽ 095.

CC X

AA A

⫽⫺()1

⫽⫺1

SSe

⫽

⫺

⫽⫺n

⫺⫽

ÚÚ

⫺⫽

GROWTH KINETICS 113

Ch005.qxd 10/27/2006 10:44 AM Page 113