Gerya T. Introduction to Numerical Geodynamic Modelling

Подождите немного. Документ загружается.

2.1 Density of rocks and minerals. Equations of state 27

(a) (b)

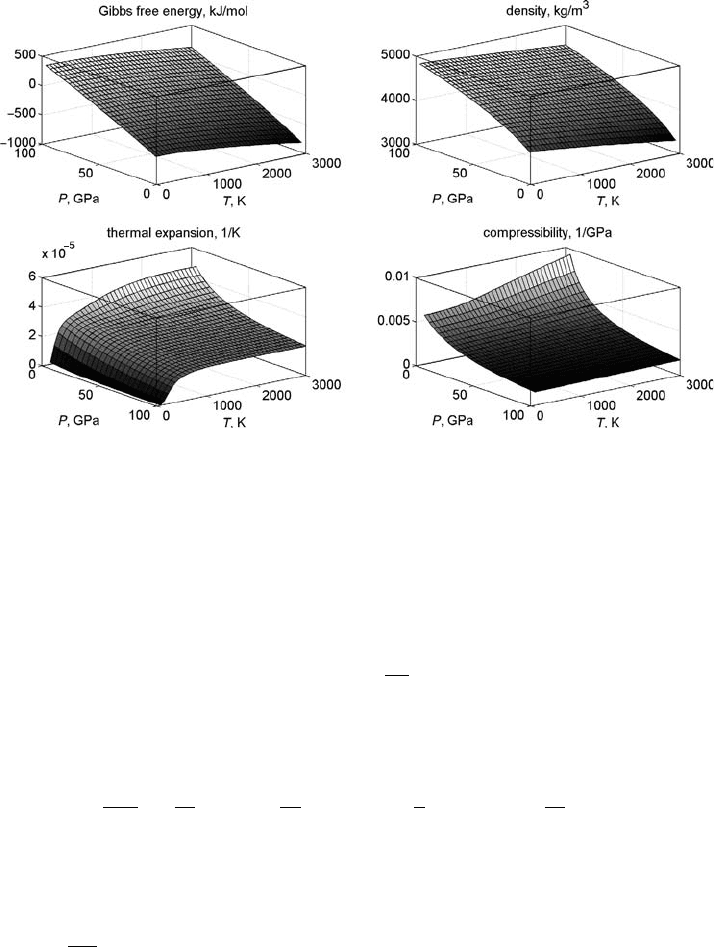
Fig. 2.1 Gibbs free energy (a), density (b), thermal expansion (c) and compress-

ibility (d) of periclase (MgO) computed on the basis of the semi-empirical param-

eterisation of Gerya et al.(2004d) for a broad range of temperature and pressure

values. Note that pressure axis in (c) and (d) is inverted compared to (a) and (b).

Results are computed with the code Periclase_EOS.m.

Murnaghan equation of state (Murnaghan, 1944)

ρ = ρ



1 + B



1/B



, (2.5)

Birch–Murnaghan equation of state (Birch, 1947)

P (ρ) =







7/3

−





5/3



1 +





− 4









2/3

− 1



(2.6)

where B

=1/β

is the bulk modulus (this quantity will be also discussed in

relation to elasticity in Chapter 12) at P = 0(β

is the compressibility at P =0),





∂B

∂P



T =const

is the pressure derivative of the bulk modulus at a constant

temperature and ρ

is the density at P =0. The Murnaghan equation is derived with

an experimentally based assumption that the pressure derivative of the bulk modulus



is independent of pressure (many substances have a fairly constant B



value of

about 3.5). The Birch–Murnaghan equation (2.6) is also derived empirically based

on measurements of volumes of solid substances, held at a constant temperature.

28 Density and gravity

Obviously, this equation has to be solved iteratively to obtain a density at a given

pressure.

Equations (2.5)and(2.6), however, do not establish the dependence of density

upon temperature, and therefore, an even more complicated EOS must be used

when the density description over a wide range of both pressure and temperature

values is needed. For example, in mineralogy and petrology, the molar volume

of minerals (V) is described in many cases by semi-empirical equations (e.g. the

Murnaghan-like EOS) with additional temperature-dependent terms (Holland and

Powell, 1998)

V = V



1 +a

(

T − T

)

+ b



√

T −







1 −



[

1 −c

(

T − T

)

]

+ B





1/B



(2.7)

where V

is molar volume at P

and T

(i.e.atareference PT-conditions)anda,

b and c are empirical parameters computed from experimental measurements of

molar volume at elevated pressures and temperatures.

It should also be mentioned that in mineralogy and petrology, self-consistent

descriptions of thermodynamic properties (including density) of minerals and ﬂu-

ids is often based on formulating the equations for their molar thermodynamic

potentials (typically either for Gibbs G

(P, T)

or for Helmholz F

(V, T)

potential, e.g.,

Karpov et al., 1976; Helgesson et al., 1978; Dorogokupets and Karpov, 1984;

Berman, 1988; Holland and Powell, 1990, 1998). Density as well as many other

physical properties (such as heat capacity, thermal expansion, compressibility, etc.)

are then computed from the potential (Fig. 2.1) using standard thermodynamic

relations

V =



∂G

(P,T)

∂P



T =cont

, (2.8)

P =−



∂F

(V,T)

∂V



T =cont

, (2.9)

V =

, (2.10)

where m is molar mass, kg/mol.

Self-consistent thermodynamic databases (e.g., Karpov et al., 1976; Helgesson

et al., 1978;Berman,1988; Holland and Powell, 1990, 1998) are often based on

the standard formulation of Gibbs free energy in the form:

m(P,T)

= H

− T ·S



Pr(T )

]dT − T ·



Pr(T )

/T ]dT +



(P,T)

]dP,

(2.11)

2.1 Density of rocks and minerals. Equations of state 29

(a)

(b)

2820

2770

2800

2760

2750

2640

2660

2670

2710

2750

2780

2810

2820

2630

2760

2770

2800

2740

2780

2720

350

0.2

0.4

0.6

0.8

0.2

0.4

0.6

0.8

450 550 650 750 850 950

T, °C

350 450 550 650 750 850 950

T, °C

P, GPa

Mu+Chl+Ep

Mu+Chl

Mu+Chl+Bt

Mu+Bt+Crd

Mu+Bt+Sil

Crd+Kfs+Grt+Opx

Crd+Kfs+Grt

Crd+Sil+Kfs+Grt

Sil+Kfs+Grt

Bt+Sil+Kfs

Mu+Bt+Ky

Bt+Sil+

Kfs+Grt

Bt+Crd+Kfs

Crd+Kfs+Opx

Bt+Crd+

Kfs+Grt

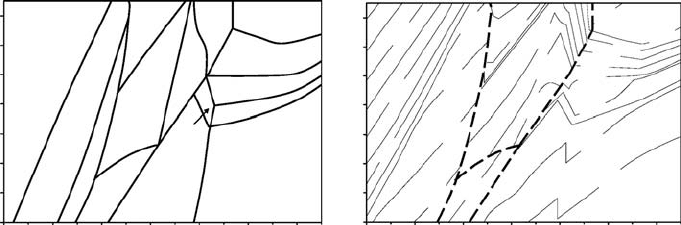
Fig. 2.2 Equilibrium mineral assemblages (a) and the corresponding density

(kg/m

) map (b) computed for a typical composition of metamorphosed aluminous

sediment (high-grade metapelite) on the basis of Gibbs free energy minimisation

(Gerya et al., 2001). Quartz, plagioclase and Fe-Ti oxides are present in all mineral

assemblages. Other minerals are: Bt = biotite, Chl = chlorite, Crd = cordierite,

Ep = epidote, Grt = garnet, Kfs = K-feldspar, Ky = kyanite, Mu = muscovite,

Opx =opthopyroxene, Sil =sillimanite. Heavy dashed lines in (b) indicate sharp

changes in density related to changes in the mineral assemblages.

where G

m(P, T)

is the molar Gibbs free energy (i.e. Gibbs potential) at a given P

and T; H

and S

are the enthalpy of formation and entropy respectively, of a

substance at standard pressure P

and temperature T

; C

Pr(T)

is the heat capacity as

a function of temperature at a standard pressure P

; V

(P, T)

is the molar volume of

substance as a function of pressure and temperature deﬁned by a semi-empirical

EOS-function (such as, for example, Eq. 2.7).

Natural rocks typically contain several different minerals and therefore the den-

sity of a rock can be calculated from its mineralogical composition as follows

rock



i=1

, (2.12)

where n is the number of different minerals in the rock, X

is the volumetric

fraction of the i-th mineral in the rock and ρ

is the density of the i-th mineral as

a function of P and T. At any given P, T and chemical composition of the rock,

both the amount and the composition of the minerals can be computed using the

concept of thermodynamic equilibrium. According to this concept, the Gibbs free

energy of the rock in an equilibrium state corresponds to a global minimum. The

amount and composition of minerals can then be obtained from internally consistent

thermodynamic databases by using the so-called Gibbs free energy minimisation

approach (e.g. Karpov et al., 1976; Dorogokupets and Karpov, 1984, Connolly and

Kerrick, 1987; de Capitani and Brown, 1987). In this case, the density of rocks in

an equilibrium state (Sobolev and Babeyko, 1994;Petriniet al., 2001;Geryaet al.,

30 Density and gravity

2001;Kauset al., 2005) can be computed from Eqs. (2.8), (2.10), (2.11) and (2.12)

by using the densities and volumetric fractions of minerals composing a computed

equilibrium mineral assemblage (Fig. 2.2). Such an approach has recently been

used to constrain coupled petrological-thermomechanical numerical geodynamic

models (e.g. Gerya et al., 2004c, 2006; Tackley, 2008;Mishinet al., 2008)which

take into account changes of rock density and thermal properties during the course

of various geodynamic processes (we will discuss the details of this approach in

Chapter 17).

2.2 Gravity and gravitational potential

The density distribution in a continuous medium is inherently related to the grav-

itational ﬁeld in this medium. This can be formulated in the form of a so-called

Poisson equation, which describes spatial changes in gravitational potential 

inside a self-gravitating continuum

∂



∂x

∂



∂y

∂



∂z

= 4πGρ

(x,y,z)

, (2.13a)

or in a different symbolic notation

 = 4πGρ

(x,y,z)

, (2.13b)

∇

 = 4πGρ

(x,y,z)

, (2.13c)

where G = 6.672 × 10

−11

(N · m

)/kg

is the gravitational constant, ρ

(x,y,z)

the spatially variable density and  (big delta), or ∇

is the Laplace operator

or Laplacian, which is a differential operator (like the divergence and gradient

operator from Chapter 1) often used in continuum mechanics for representing the

sum of second-order partial derivatives of a variable A

In 1D: A =∇

A =

∂

∂x

, (2.14a)

In 2D: A =∇

A =

∂

∂x

∂

∂y

, (2.14b)

In 3D: A =∇

A =

∂

∂x

∂

∂y

∂

∂z

. (2.14c)

The gravitational potential (J/kg), characterises the amount of potential energy

per unit mass for a given location, related to the interaction of the local mass with all

other surrounding masses. Another interpretation of  is the amount of work needed

to be done to move a unit mass (i.e. overcoming its gravitational interactions with

surrounding masses) from a given location to inﬁnity (where no interactions with

2.2 Gravity and gravitational potential 31

other masses occur). Since such work is always positive, the amount of potential

energy and therefore the gravitational potential is maximal at inﬁnity. The relative

gravitational potential (i.e. changes in potential energy relative to inﬁnity) will then

always be negative.

The Poisson equation (2.13) can be derived from Newton’s law of gravitation

which quantiﬁes the gravitational attraction force f

acting between two bodies

with masses m

and m

, separated by a distance r

= G

, (2.15a)

or in 3-D vector notation

= G

(

− x

)

, (2.15b)

= G

(

− y

)

, (2.15c)

= G

(

− z

)

, (2.15d)

= G

(

− x

)

, (2.15e)

= G

(

− y

)

, (2.15f)

= G

(

− z

)

, (2.15g)

where f

, f

and f

are components of the gravitational force vector

acting

on mass m

and g

, g

and g

are components of gravitational acceleration

vector

felt by mass m

(in accordance with the second Newton’s law of motion,

acceleration can be deﬁned as the amount of force per unit mass, g

The simpliﬁed explanation of such a derivation is the following. Firstly, we

should realize that local derivatives of gravitational potential by the spatial co-

ordinates are equal to the respective components of the gravitational acceleration

vector g, taken with a negative sign

∂

∂x

=−g

, (2.16a)

∂

∂y

=−g

, (2.16b)

∂

∂z

=−g

. (2.16c)

The minus sign in the right-hand side of equations (2.16a)–(2.16c) reﬂects the fact

that the potential energy  should increase in the direction opposite to the direction

of the local gravity force, i.e. work contributing to the increase in potential energy

32 Density and gravity

has to be done by applying a force



f in the opposite direction compared to the

local gravity force

d

= f

dx =−g

dx, (2.17a)

d

= f

dy =−g

dy, (2.17b)

d

= f

dz =−g

dz, (2.17c)

where d

,d

and d

are increments in potential energy of a given unit mass

due to small changes (dx,dy and dz) in the respective coordinates of this unit

mass. According to Newton’s law of gravitation (Eq. 2.15), the acceleration (i.e.

gravitational force per unit mass)

g = (g

) felt at any given point within a

continuum with coordinates x, y, z due to the gravitational attraction from surround-

ing masses is obtained by summing up (i.e. integrating) the accelerations exerted

by each small mass element (δm

), as follows

∞



i=1

δm

(

− x

)

, (2.18a)

∞



i=1

δm

(

− y

)

, (2.18b)

∞



i=1

δm

(

− z

)

, (2.18c)



(

− x

)

(

− y

)

(

− z

)

, (2.18d)

where x

, y

, z

are the coordinates of the i-th mass element and r

is the dis-

tance between this element and the given point. The divergence of the integrated

acceleration ﬁeld at a given point can be then computed as follows (verify as an

exercise)

−  =

∂

∂x



−

∂

∂x



∂

∂y



−

∂

∂y



∂

∂z



−

∂

∂z



= div(

g) =

∂g

∂x

∂g

∂y

∂g

∂z

, (2.19a)

div(

g) =

∞



i=1

Gδm



∂

∂x



x − x



∂

∂y



y − y



∂

∂z



z −z



, (2.19b)

div(

g) =

∞



i=1

Gδm



(

x − x

)

−





(

y − y

)

−





(

z −z

)

−



, (2.19c)

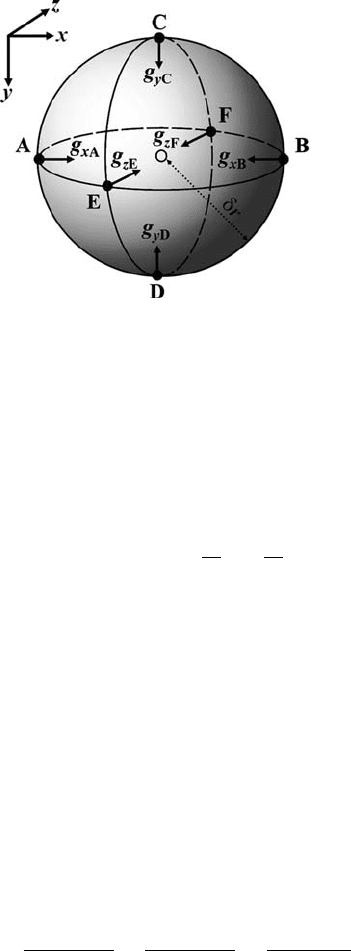
2.2 Gravity and gravitational potential 33

Fig. 2.3 Sphere of radius δr and mass δm considered for the derivation of the Pois-

son equation. Black arrows show respective components of gravitational accelera-

tion vector felt at the surface of the sphere in six different points (black dots, A, B,

C, D, E and F). Open circle shows the centre of the sphere in which the divergence

of the gravitational acceleration is computed.

and ﬁnally by using Eq. (2.18)

div(

g) =

∞



i=1

Gδm



− 3



. (2.19d)

Note that differentiation is done with respect to the coordinates x, y, z of the given

point and not by those of the surrounding masses (x

, y

, z

) which are independent

of x, y, z.

For all r

= 0, Eq. (2.19d) is obviously zero. This means that the divergence of

gravitational acceleration at a given point is independent of the surrounding masses

and must come from the point itself (i.e. for x = x

, y = y

, z = z

and r

= 0).

Then one may restrict the volume of integration to a small sphere with mass δm

and radius δr centred on this point (Fig. 2.3). The divergence of acceleration for

this small sphere can be approximated by differences with the use of six points (A,

B, C, D, E and F, Fig. 2.3) located on the sphere as follows

div( g) =

− g

2δr

− g

2δr

− g

2δr

, (2.20)

where g

−g

are the respective components of the acceleration vector at different

points on the sphere’s surface. Density inside the sphere can be considered constant

since the mass inside the small sphere is uniform. Therefore, at the considered six

points, the respective components obviously coincide with the acceleration vectors

directed toward the centre of the sphere and can be computed from the common

34 Density and gravity

gravity formula for a sphere (see Turcotte and Schubert, 2002, Eqs. (5–1)–(5–15))

= g

= G

δm

δr

, (2.21a)

= g

=−G

δm

δr

. (2.21b)

Combining Equations (2.14)and(2.15) and taking into account that the average

density inside the sphere with volume V =

πδr

is given by ρ =

δm

3δm

4πδr

under the condition that δr tend to zero we obtain the Poisson equation (verify as

an exercise)

 =−div(

g) = 3G

δm

δr

= 4πGρ. (2.22)

It should be noted that our derivation is simpliﬁed and uses a standard expression

(Eq. (2.21)) for the gravitational acceleration at the surface of the sphere, which

can in turn be obtained by integrating Equation (2.18) for a point outside the sphere

(see Turcotte and Schubert, 2002, Eqs. (5–1)–(5–15) for details of this derivation).

It can also be shown on the basis of Gauss’s theorem that one can consider not only

a spherical geometry, but any arbitrary shape of the local mass and still obtain the

same Poisson equation.

Analytical exercise

Exercise 2.1

Molar Gibbs potential of periclase (MgO, molar mass m =0.0403044 kg/mol) is

given by the following equation (Gerya et al., 2004d)

m(P,T)

= H

+ V

 +



i=1

[RT ln(

− e

) − H

/(l − e

)],

= exp[−(H

+ V

)/RT ],

= exp(−H

/RT

 = 5/4(

+ φ)

1/5

[(P + φ)

4/5

− (P

+ φ)

4/5

where R =8.314 J/mol is the gas constant, P

=100 000 Pa and T

=298.15 K

are the reference pressure and temperature respectively, and H

=−601 500.00

J, V

=1.122 28 ×10

−5

J/Pa, φ =30 179 500 000 Pa, c

=1.966 12, c

=4.12 756,

Programming exercises and homework 35

=0.536 90, H

=2966.88 J, H

=5621.69 J, H

=27 787.19 J, V

V

=3.52971 ×10

−8

J/Pa, V

=1.984 956 8 ×10

−6

J/Pa are empirical param-

eters.

Derive expressions for the density ρ, thermal expansion α and compressibility

β as functions of pressure and temperature (Fig. 2.1) using the equations given in

this chapter.

Programming exercises and homework

Exercise 2.2

Compute and visualise as colour maps with isolines (pcolor, contour, contourf)and

surfaces (surf, light, lighting) the density ρ, thermal expansion α and compress-

ibility β for periclase (Fig. 2.1) based on the equations derived for the analytical

exercise. Take a temperature interval from 100 to 4000 K and a pressure interval

from 10

to 10

Pa (1 to 100 GPa). Try also to deﬁne the Gibbs free energy

equation as an external function G

m(P, T)

and use differences instead of derivatives

to compute V

(P, T)

, ρ

(P, T)

, α

(P, T)

and β

(P, T)

(P,T)

, where

(P,T)



∂G

m(P,T)

∂P



T =const

≈

G

m(P,T)

P

m(P +P ,T )

− G

m(P,T)

P

(P,T)

=−

(P,T)

∂ρ

(P,T)

∂T

≈−

(P,T)

ρ

(P,T)

T

=−

(P,T)

(P,T+T )

− ρ

(P,T)

T

(P,T)

∂ρ

(P,T)

∂P

≈

(P,T)

ρ

(P,T)

P

(P,T)

(P +P ,T )

− ρ

(P,T)

P

where P and T are small increments in pressure and temperature, respectively.

Compare the results based on differences with your analytical solutions. An

example is in the code Periclase_EOS.m which calls function G_periclase.m.

Exercise 2.3

Load from ﬁles (fopen, fscanf, fclose) and visualise (pcolor) density maps (Mishin

et al., 2008) corresponding to the phase diagrams computed for pyrolite (mantle, ﬁle

m895_ro) and MORB (oceanic crust, ﬁle morn_ro) based on a Gibbs free energy

minimisation approach. Compute and visualise the density difference between

these two contrasting types of rocks at various P–T parameters. Check at which P

and T this difference is maximal/minimal.

The ﬁrst nine positions in the data ﬁles are as follows

pl8951 350 350 800.003 10001.5 9.16904 4269.33 T(K) P(bar)

36 Density and gravity

where pl8951 denotes the rock identiﬁcation (skip that); 350 and 350 are resolutions

for T and P respectively; 800.003 and 10001.5 are starting value for T (K) and P

(bar, 1 bar = 10

Pa), respectively; 9.16904 and 4269.33 are steps for T (K) and P

(bar), respectively; T (K) and P (bar) are P and T identiﬁcations (to skip). Further

data in the ﬁles are 350 ×350 maps of rock density (kg/m

)atvariableT (inner

cycle) and P (outer cycle). An example is in Density_map.m.