Гераськин М.И. Математическая экономика: теория производства и потребительского выбора

Подождите немного. Документ загружается.

§4.6. Различные типы благ (товаров)

К о э ф ф и ц и е н т ч у в с т в и т е л ь н о с т и с п р о с а

п о ц е н е

∂

показывает, на сколько единиц изменится

спрос на данный товар, если его цена увеличится на 1 рубль.

К о э ф ф и ц и е н т ч у в с т в и т е л ь н о с т и с п р о с а п о д о х о д у

∂

показывает, на сколько единиц изменится спрос на данный товар, если доход

потребителя увеличится на 1 рубль. В соответствии со знаками показателей

чувствительности блага могут быть отнесены к одному из следующих типов:

1. Н о р м а л ь н ы е и ц е н н ы е блага:

∂

то есть спрос на

благо снижается при увеличении его цены и возрастает при увеличении дохода

потребителяример: масло.)

2. Н о р м а л ь н ы е и м а л о ц е н н ы е блага:

∂

то есть спрос

на благо снижается как при увеличении его цены, так и при росте дохода

потребителя. Например, ценным благом может считаться масло, а малоценным

– маргарин.

3. «Т о в а р ы Г и ф ф и н а » :

∂

это означает, что спрос на благо растет

при увеличении его цены. Товары Гиффина

являются малоценными.

Примером товаров Гиффина может служить труд низко квалифицированных

работников для небольших предприятий как потребителей: при повышении

цены блага (минимальной оплаты труда), предприятие, не имея возможности

приобрести технологичное оборудование в связи с бюджетным ограничением

вынуждено нанимать еще больше низкооплачиваемых работников. Другой

пример товаров Гиффина: продовольственные товары в комбинации с одеждой

- повышение цены на продукты приводит к тому, что реальный доход

потребителя снижается настолько, что он не может потреблять прежнее

количество одежды и вынужден большую часть дохода расходовать на

продукты.

Таким образом, главная особенность товаров Гиффина – их

Роберт Гиффин (1878-1943) – английский экономист, исследовавший проблемы потребительского выбора.

Коэффициенты

чувствительности

о т н о с и т е л ь н а я д е ш е в и з н а по сравнению с возможными аналогами.

Безразмерные показатели чувствительности комбинации

благ к изменению параметров рынка получили название

коэффициентов эластичности.

Э л а с т и ч н о с т ь с п р о с а п о д о х о д у показывает, на сколько

процентов изменится объем потребления блага при изменении дохода на 1 %:

⋅

∂

=Ε

В соответствии со значениями

различают следующие типы благ, кривые

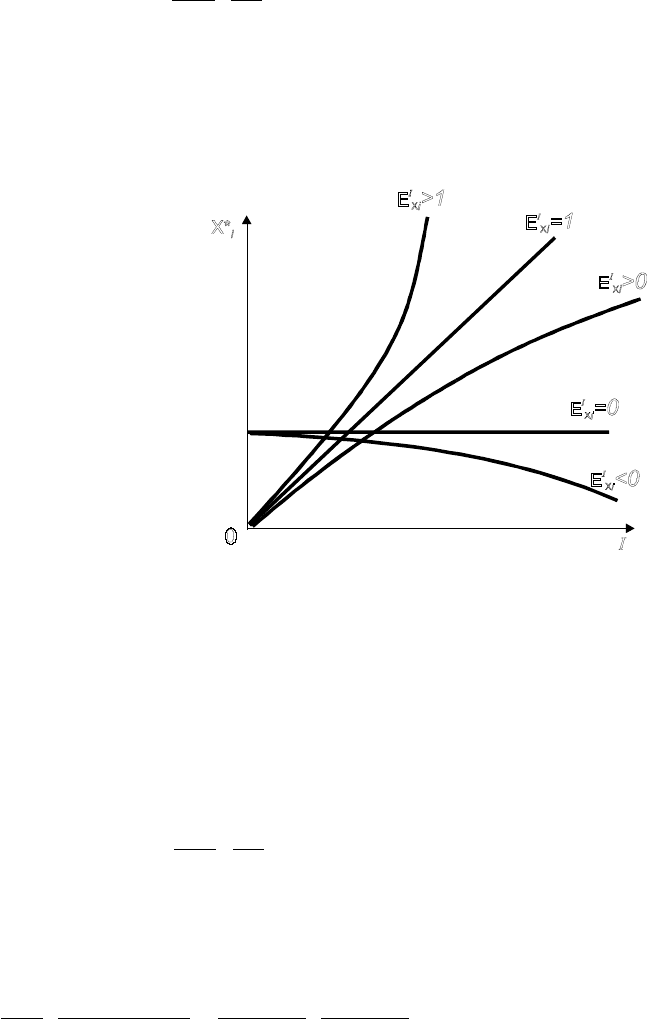
«доход-потребление» которых приведены на рис. 4.11:

1. Н и з к о к а ч е с т в е н н ы е ( м а л о ц е н н ы е ) б л а г а , спрос на которые

падает с увеличение дохода:

<Ε

2. Б л а г а п е р в о й

н е о б х о д и м о с т и , потребление

которых не зависит от изменения

дохода:

=Ε

3. К а ч е с т в е н н ы е ( ц е н н ы е )

б л а г а , объем потребления которых

увеличивается с ростом дохода:

>Ε

Рис. 4.11. Кривые «доход-потребление»

4. П р е д м е т ы р о с к о ш и , потребление которых растет опережающими

темпами по сравнению с увеличением дохода:

>Ε

Э л а с т и ч н о с т ь с п р о с а п о ц е н е показывает на сколько

процентов изменится объем потребления блага при изменении его цены на 1 %:

⋅

∂

=Ε

При существенных колебаниях рыночных цен используют формулу средней

эластичности:

( )

*''

рр

2/xx

2/рр

⋅

−

⋅

∆

=Ε

. (4.20)

На карте кривых «цена-потребление» (кривых спроса на рис. 4.12)

коэффициент эластичности позволяет различить блага следующим образом:

1 . Н о р м а л ь н ы е б л а г а , которые приобретаются в больших объемах по

Коэффициенты

эластичности

меньшей цене:

<Ε

В том числе вполне заменяемые блага, спрос на

которые бесконечно падает при малом увеличении цены:

− ∞=Ε

2 . Н е з а м е н и м ы е б л а г а ,

изменение цены которых не влияет на

объем потребления (спрос совершенно

не эластичен):

=Ε

3 . Т о в а р ы Г и ф ф и н а , спрос на

которые растет с увеличением цены:

>Ε

Блага Гиффина с совершенно

эластичным спросом невозможны ввиду

бюджетного ограничения.

Рис. 4.12. Кривые «цена-потребление»

П е р е к р е с т н а я э л а с т и ч н о с т ь с п р о с а п о ц е н е

показывает процентное изменение спроса на одно благо при 1-процентном

изменении цены другого:

⋅

∂

=Ε

В соответствии с значением этого коэффициента блага могут быть

взаимозаменяемыми

( )

>Ε

, взаимодополняемыми

( )

<Ε

или

независимыми

( )

=Ε

Пример 4.6.1. Рыночная цена масла животного возросла с 80 руб. за кг до 100

руб., вследствие чего средний потребительский спрос на него упал с 5 кг в

месяц до 4 кг в месяц. Насколько эластичен спрос на масло?

Определим коэффициент эластичности спроса на масло по формуле

(4.20):

10080

рр

*''

−=

⋅

−

⋅

−

=Ε

. Таким образом, при

повышении цены масла на 1% спрос на него снижается на 1%. То есть масло

относится к нормальным благам, спрос на которые существенно эластичен.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ 4.1. Анализ функции полезности

4.1.1. Предпочтения потребителя описываются логарифмической функцией полезности с

коэффициентами а

=2, а

=3, х

=0,5, х

=1. На сколько единиц повысится удовлетворенность

потребителя, если он потребляет 5 кг мяса (1-ый товар) и изнашивает 3 пары носков (2-ой

товар) в месяц, и решил купить дополнительную пару носков?

4.1.2. Решить задачу 4.1.1, если у потребителя степенная функция полезности с

коэффициентами А=10, b

=0,3, b

=0,7, х

=0,1, х

=0,2. Потребитель решил купить

дополнительно 1 кг мяса, а носки использует в неизменном количестве.

4.1.3-4.1.4. В задачах 4.1.1, 4.1.2 построить график кривой полезности мяса (при постоянном

количестве используемых носков). Графически объяснить предельную полезность.

4.1.5. Потребитель в задаче 4.1.1 приобретает 5 кг мяса в месяц. Сколько пар носков он

должен изнашивать ежемесячно, чтобы его удовлетворенность составила 10 единиц.

4.1.6. Потребитель в задаче 4.1.2 изнашивает 3 пары носков в месяц. Сколько мяса он должен

покупать ежемесячно, чтобы быть удовлетворенным на 30 единиц?

4.1.7. Степень удовлетворенности потребителя из задачи 4.1.1 равна 2 единицы. Сколько он

потребляет мяса и изнашивает носков ежемесячно, если он согласен за лишний кг мяса

отказаться от 4-х пар носков? Построить график кривой безразличия. Показать

геометрический смысл нормы замены.

4.1.8. Степень удовлетворенности потребителя из задачи 4.1.2 равна 10 единиц. Сколько он

потребляет товаров, если взамен на две пары носков он согласен есть на 1 кг мяса меньше?

Построить график кривой безразличия. Показать геометрический смысл нормы замены.

ПРАКТИЧЕСКОЕ ЗАДАНИЕ 4.2. Решение задачи потребительского выбора

4.2.1. Потребитель из задачи 4.1.1 имеет доход 300 рублей в месяц, цена мяса 50 рублей за кг,

цена носков 20 рублей за пару. Решить задачу потребительского выбора графически и

аналитически.

4.2.2. Потребитель из задачи 4.1.2 имеет доход 600 рублей в месяц, цена мяса 100 рублей за

кг, цена носков 30 рублей за пару. Решить задачу потребительского выбора графически и

аналитически.

4.2.3. Цены в задаче 4.2.1 возросли: мяса на 10%, носков – на 20%. Государственный бюджет

компенсирует потери потребителя в виде дотации, сумму которой требуется определить.

4.2.4. Цены в задаче 4.2.2 возросли: мяса на 5%, носков – на 10%. Найти размер дотации,

которая полностью компенсирует потери потребителя.

4.2.5. Цена на мясо снизилась со 100 рублей за кг до 90 рублей за кг, вследствие чего спрос

на него возрос с 2 кг в месяц до 4 кг в месяц . Найти среднюю эластичность спроса по цене.

4.2.6. Цена на обувь возросла с 700 рублей за пару до 1000 рублей за пару, в результате чего

спрос на нее упал с 3 пар в год до 2 пар в год. Найти среднюю эластичность спроса по цене.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Ашманов С.А. Введение в математическую экономику. – М.: Наука, 1984. – 296 с.

2. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике:

учебник. – М.: МГУ им. М.В. Ломоносова, 1998. – 368 с

3. Интрилигатор М. Математические методы оптимизации и экономическая теория. – М.:

Прогресс, 1975.- 605 с.

4. Гришанов Г.М., Гераськин М.И. Математические основы экономической теории

производства. – Самара, Самар. гос. аэроком. ун-т, 2001. – 102 с.

100

РЕКОМЕНДАЦИИ ПО ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ

♦Курс «Математическая экономика» охватывает 2 семестра, в каждом из

которых необходимо решить две контрольных работы: в первом семестре

студенты решают контрольные работы 1,2, во втором семестре – контрольные

работы 3,4. Выполненные контрольные работы сдаются в деканат факультета

заочного обучения, причем на каждую контрольную работу должен быть

выписан отдельный учетный талон.

♦ВЫБОР НОМЕРА ВАРИАНТА: номер варианта №, фигурирующий в

заданиях к контрольным работам, соответствует номеру студента в списке

группы.

♦Контрольную работу следует выполнять на листах формата А4; пример

оформления титульного листа приводится в учебном пособии (стр. 104);

страницы должны быть пронумерованы и иметь поля для замечаний

рецензента; текст должен быть написан разборчиво, без зачеркиваний и

исправлений; графики рисуются с использованием линейки и цветных

карандашей; в конце работы должен быть список использованной литературы.

♦При оформлении решения каждой задачи в контрольной работе должна

приводится краткая информация по соответствующему разделу теоретического

курса. Применение каждой формулы должно быть объяснено. При

вычислениях необходимо привести расчетную формулу, численное

представление расчетной формулы, результат вычислений и экономическую

интерпретация результата.

♦При отчете по контрольной работе студент должен знать теоретические

положения, использованные при решении каждой задачи, а также свободно

ориентироваться в процессе решения задачи.

КОНТРОЛЬНАЯ РАБОТА 1

Определение коэффициентов и характеристик производственной функции

1.1. Автотранспортная фирма за последние 5 лет характеризовалась следующими

показателями хозяйственной деятельности:

Год

Объем перевозок, тонн×км

Количество автомобилей, ед. Численность работников, чел.

1 1200/№ 3 9

2 1700/№ 5 10

3 2800/№ 8 18

4 3500/№ 10 22

5 4800/№ 14 30

Построить графики кривых выпуска, на основе которых подобрать вид ПФ. Определить

значения коэффициентов ПФ, объяснить их экономический смысл. Спрогнозировать объем

перевозок в 6-й год, если запланировано довести количество автомобилей до 20 ед.,

численность работников до 35 чел.

1.2. Железобетонный завод за последние 5 лет характеризовался следующими показателями

хозяйственной деятельности:

Год Объем выпуска бетона, тонн Количество бетонных установок,

единиц

Численность работников,

чел.

101

1 500/№ 1 3

2 900/№ 2 10

3 1200/№ 3 14

4 1400/№ 4 20

5 1500/№ 5 25

Построить графики кривых выпуска, на основе которых подобрать вид ПФ. Определить

значения коэффициентов ПФ, объяснить их экономический смысл. Спрогнозировать объем

выпуска в 6-й год, если запланировано довести количество установок до 8 ед., численность

работников до 35 чел.

1.3. При сборке печатной платы используется 20/№ чипов и 60/№ соединительных проводов.

Построить графики кривых выпуска, если на сборку подано а) 30000/№ чипов; б) 120000/№

соединительных проводов. Определить значения коэффициентов ПФ, объяснить их

экономический смысл.

1.4-1.6. Для ПФ в задачах 1.1-1.3 получить выражения среднего и предельного продуктов, а

также коэффициентов эластичности по ресурсам. Изобразить графически зависимости

экономико-математических характеристик, как функций соответствующего ресурса. В

задачах 1.1,1.2 вычислить значения экономико-математических характеристик по данным 5-

го и 6-го года работы, объяснить их экономический смысл, сопоставить эффективность

работы в эти годы.

КОНТРОЛЬНАЯ РАБОТА 2

Функция издержек в долгосрочном и краткосрочном периодах

2.1. Меховая фирма для изготовления шапок использует меховые шкурки по цене 800/

(1+0,01№) руб. за шкурку и обратную кожу по цене 600/(1+0,01№) руб. за шкурку.

Коэффициенты эластичности выпуска по ресурсам равны 0,5/(1+0,01№) и 0,7/(1+0,01№)

соответственно, А=1. Определить функции спроса на ресурсы и функцию издержек, если

потребление ресурсов не ограничено и технология описывается ПФ Кобба-Дугласа.

Построить графики функций спроса на ресурсы и функции издержек.

2.2. Решить задачу 2.1 графическим методом, построив линию долговременного развития.

2.3. В задаче 2.1 определить функции предельных и средних издержек. Построить графики.

2.4. Решить задачу 2.1, если расход обратной кожи по условиям договора с поставщиком

ограничен объемом 1000/(1+0,01№) шкурок в месяц.

2.5. Решить задачу 2.4 графическим методом.

2.6. В задаче 2.4 определить функцию средних издержек. Построить график.

КОНТРОЛЬНАЯ РАБОТА 3

Оптимизация прибыли фирмы

3.1. Фирма «Стройкерамика» использует глину по цене 2/(1+0,01№) руб. за кг и краситель по

цене 8/(1+0,01№) руб. за кг и продает кирпич по цене 100*(1+0,01№) руб. за штуку.

Коэффициенты ПФ равны:

5,0

=α

5,0

=β

, А=(10+№). Определить функции спроса на

ресурсы, оптимальный объем выпуска и максимальное значение прибыли в долгосрочном

периоде.

3.2. Решить задачу 3.1 для случаев: а) возрастающей отдачи от расширения масштаба

0,6= ;8,0

β=α

; б) убывающей отдачи от расширения масштаба

0,6= ;2,0

β=α

; в)

отсутствия эффекта расширения масштаба

0,7= ;3,0

β=α

3.3-3.4. Решить задачи 3.1-3.2 в условиях краткосрочного периода, если объем затрат первого

ресурса зафиксирован – закупки глины ограничены объемом 10*(1+0,01№) кг.

3.5. Фирма–монополист производства хрустальных ваз оплачивает песок по цене 3/

(1+0,01№) руб. за кг и цинк по цене 8/(1+0,01№) руб. за кг. Цена продукции определяется

выражением: р

=1000-0,1Q (руб. за вазу). Определить оптимальный объем выпуска в случае

А=1 и а) при убывающей отдаче от расширения масштаба

0,4= ;1,0

β=α

; б) при отсутствии

эффекта расширения масштаба

0,6= ;4,0

β=α

. Найти оптимальный с точки зрения

102

прибыли объём выпуска. Определить спрос на ресурсы и найти максимальную прибыль.

Построить графики дохода, издержек, прибыли.

3.6. Решить задачу 3.5 для случаев: а)

0,2= ;3,0

β=α

; б)

0,5= ;5,0

β=α

КОНТРОЛЬНАЯ РАБОТА 4

Моделирование потребительского выбора

4.1. Предпочтения потребителя описываются логарифмической функцией полезности с

коэффициентами а

=2*(1+0,01№), а

=3*(1+0,01№), х

=0,5/(1+0,01№), х

=1/(1+0,01№). На

сколько единиц повысится удовлетворенность потребителя, если он потребляет 4*(1+0,01№)

кг колбасы (1-ый товар) и использует 3*(1+0,01№) куска мыла (2-ой товар) в месяц, и решил

купить дополнительно кусок мыла?

4.2. Решить задачу 4.1, если у потребителя степенная функция полезности с коэффициентами

А=10*(1+0,01№), b

=0,4, b

=0,5, х

=0,2/(1+0,01№), х

=0,3/(1+0,01№). Потребитель решил

купить дополнительно 1 кг колбасы, а мыло использует в неизменном количестве.

4.3-4.4. В задачах 4.1, 4.2 построить графики кривых полезности товаров. Дать графическую

интерпретацию предельной полезности.

4.5. Потребитель в задаче 4.1 приобретает 4*(1+0,01№) кг колбасы в месяц. Сколько кусков

мыла он должен использовать ежемесячно, чтобы его удовлетворенность составила

10*(1+0,01№) единиц.

4.6. Степень удовлетворенности потребителя из задачи 4.2 равна 10*(1+0,01№) единиц.

Сколько он потребляет товаров, если взамен на 0,5*(1+0,01№) кг колбасы он согласен

отказаться от 2*(1+0,01№) кусков мыла? Построить график кривой безразличия. Показать

геометрический смысл нормы замены.

4.7. Потребитель из задачи 4.2 имеет доход 500*(1+0,01№) рублей в месяц, цена колбасы 60/

(1+0,01№) рублей за кг, цена мыла 30/(1+0,01№) рублей за кусок. Решить задачу

потребительского выбора графически и аналитически.

4.8. Цены в задаче 4.7 возросли: колбасы на 10*(1+0,01№)%, мыла – на 15*(1+0,01№)%.

Государственный бюджет полностью компенсирует потери потребителя в виде дотации,

сумму которой требуется определить.

4.9. Цена на колбасу возросла с 60/(1+0,01№) рублей за кг до 80/(1+0,01№) рублей за кг,

вследствие чего спрос на нее упал с 2*(1+0,01№) кг в месяц до 4*(1+0,01№) кг в месяц.

Найти среднюю эластичность спроса по цене.

103

Образец титульного листа контрольной работы

Министерство образования и науки Российской Федерации

Самарский государственный аэрокосмический университет

имени академика С.П. Королева

Факультет заочного обучения

КОНТРОЛЬНАЯ РАБОТА №1

ПО КУРСУ «МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА»

тема «Определение коэффициентов и характеристик производственной

функции»

Выполнил:

студент группы____ Петров А.И.

Проверил:

доцент Гераськин М.И.

Самара 2004

104

Учебное издание

Гераськин Михаил Иванович

МАТЕМАТИЧЕСКАЯ ЭКОНОМИКА:

ТЕОРИЯ ПРОИЗВОДСТВА

И ПОТРЕБИТЕЛЬСКОГО ВЫБОРА

Учебное пособие

Самарский государственный аэрокосмический университет имени академика С.П. Королева

443086, Самара, Московское шоссе, 34