Геодезические линии для метрики Шварцшильда
Подождите немного. Документ загружается.

Оглавление
Введение ………………..……………………………………………………....3
1. Математическое определение геодезических. Уравнение
геодезических…………………………………………………………………….4
2. Метрический тензор…………………………………………………………..7
3. Времениподобные геодезические для метрики Шварцшильда……………8
Радиальные геодезические……………………………………………….11
4. Изотропные геодезические для метрики Шварцшильда…………………..15
Радиальные геодезические………………………………………………16
Заключение……………………………………………………………………....17
Литература………………………………………………………………………18
1
Введение
Основной задачей данной курсовой работы будет анализ точных
количественных соотношений следующих из уравнений для геодезических
линий в пространстве-времени Шварцшильда. Другими словами, в работе
будут рассматриваться траектории пробных свободно падающих частиц на
не вращающуюся черную дыру, которая описывается метрикой
Шварцшильда.
Данная задача может найти свое применение, например при поиске черных
дыр, т.к. ее непосредственное наблюдение невозможно, но ее можно
обнаружить лишь по косвенным параметрам. В астрофизических моделях это
может быть, например, рассмотрение аккреционного диска вокруг
сверхплотного компактного тела в тесной двойной системе. В такой модели
излучение генерируется в процессе нагревания падающего на дыру
ионизированного газа и ускорения его в сопутствующем магнитном поле.
При исследовании газодинамических и радиационных процессов в
окрестности компактных вращающихся астрофизических объектов возникает
вопрос о характере движения пробных тел и распространения излучения в их
сильных гравитационных полях. Согласно ОТО, пробные тела в
гравитационном поле движутся по геодезическим линиям.
Геодезические линии являются мировыми линиями свободного движения, т.
е. движения, которое управляется только гравитационным полем,
описываемым данной геометрией. При этом времениподобные геодезические
являются траекториями свободного движения пробных тел, а нулевые
геодезические — свободного движения фотонов, т. е. распространения
излучения, пока его длина волны намного меньше характерного масштаба
изменения поля. Геометрия пространства-времени, создаваемая массивным
телом, описывается метрикой Шварцшильда.
В первом разделе кратко рассказывается о параллельном переносе в
искривленном пространстве-времени, дается строгое математическое
определение геодезических с его геометрической интерпретацией. И в конце
раздела предложен один из вариантов вывода уравнения геодезических.
Во втором разделе вводится понятие метрического тензора.
В последующих разделах непосредственно рассматриваются геодезические
линии: времениподобные и изотропные ( для каждого из случаев
рассматриваются радиальные геодезические)
2

Математическое определение геодезических. Уравнение геодезических.
Пусть Y — контравариантное векторное поле. Eго изменение вдоль кривой λ
на многообразии М - δY можно рассматривать как перенос вектора Y вдоль
кривой, который вызван изменением параметра t→t + δt на данной кривой λ.
Приращение век-
вектора δY равно
,
( ( ))
k
j
j
k
dx t
Y Y t
dt
(0)
В евклидовой геометрии в декартовой системе координат вектор Y
«переносится параллельно» вдоль кривой λ, если δY = 0. Но между плоским
пространством-временем и искривленным есть связь, которая отражается в
принципе эквивалентности: «Законы физики в любой локально лоренцевой
системе искривленного пространства-времени точно такие же, как и в
глобальной лоренцевой системе плоского пространства-времени». В общем
случае дифференцируемого многообразия можно дать аналогичное
определение: вектор Y переносится параллельно вдоль кривой λ, если
( ( ))
( ) ( )
k
k
j j
dx t
DY Y t
dt
(1)
Где
- аффинная связность, которая для каждого векторного поля Х на
многообразии М задает дифференциальный оператор
k
, отображающий
произвольное векторное поле Y в векторное поле
k
Y
. Аффинную
связность можно расписать в следующем виде:
,
( )
k
j j l j j l j
k lk k lk
Y Y Y Y Y
(2)
Подставим уравнение (2) в выражение (1), в результате чего получаем:
,
( ( ))
( ) 0
k
j l j
k lk
dx t
Y Y t
dt
(3)
Из выражения (3) следует, что изменение вектора Y при параллельном
переносе вдоль кривой λ равно
( ( ))
( )
k
j l j
lk
dx t
Y Y t
dt
(4)
В частности, чтобы касательный вектор
( ( ))
k
dx t
t
dt
кривой λ параллельно
переносился вдоль λ, необходимо выполнение следующего равенства:
( ( )) ( ( )) ( ( ))
( )
k l k
j
lk
dx t dx t dx t
t
dt dt dt
(5)
Кривая λ на М называется геодезической, если касательный вектор к этой
кривой при параллельном переносе остается пропорциональным самому
себе, т. е.
3
2
2
( ( )) ( ( )) ( ( ))
( ( )) ( ( ))
1 ( ) ( )
j l k
j
lk
j j
dx t dx t dx t
t
dt dt dt
dx t d x t
t t t
dt dt
(6)
Где
( )t
- некоторая функция t .
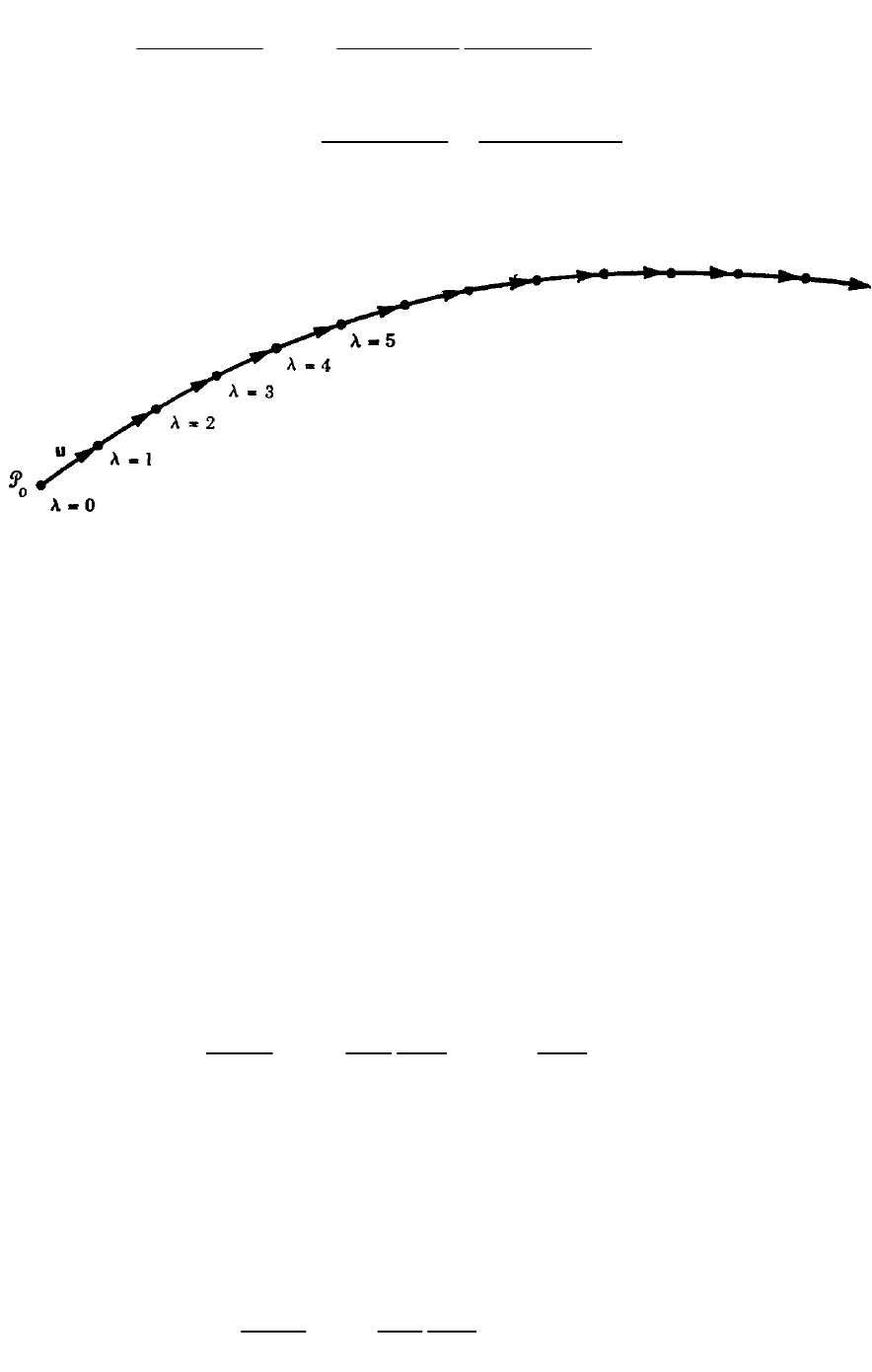
Геометрически это можно иллюстрировать следующим образом:
Геодезическую можно трактовать, как правило «прямолинейного
параллельного
переноса». Выбрав точку в 4-пространстве, в которой существует
касательный вектор u можно построить единственную геодезическую x(λ),
которая проходит через событие P
0
. Эту геодезическую можно считать
правилом, согласно которому касательный вектор u откладывается из P
0
,
далее как можно более прямо из точки P
1
(т.е. конца вектора u) снова
откладывается вектор u и т.д. Эта последовательность операций
эквивалентна параллельному переносу касательного вектора.
Т.е. можно сказать, что геодезическая описывает движение частицы в
гравитационном поле такое, что ее мировая точка перемещается по
экстремальной линии в 4-пространстве.
Устремив δt→0 в выражении (6) можно получить следующее уравнение
геодезической:
2
2
( )
j l k j
l
lk
d x dx dx dx
t
dt dt dt dt
(7)
В целях упрощения выражения (7) заменим параметр t вдоль кривой λ новым
параметром s равным:
''
''exp ' ( ')
t t
s dt dt t
(8)
то уравнение геодезических примет более простой вид:
2
2
0
j l k
l
lk
d x dx dx
ds ds ds
(9)
Параметр s называется аффинным. Следует отметить, что аффинный
параметр определен однозначно с точностью до сдвига начала отсчета.
4
По сути, уравнение геодезических – это уравнение, описывающее движение
частицы при наличии гравитационного поля (т.е. в случае негалилеева
пространства-времени).
Уравнение геодезических можно также получить из принципа наименьшего
действия или путем соответствующего обобщения дифференциальных
уравнений свободного движения частицы в галилеевой 4-системе координат.
Рассмотрим более подробно второй предложенный способ.
Уравнения специальной теории относительности выглядят следующим
образом:
0
i
du
(10)
Где
i
i
dx
u
ds
- 4-скорость
В криволинейных координатах уравнение (10) можно записать следующим
образом:
0
i
Du
(11)
Воспользуемся выражением для ковариантного дифференцирования вектора:
( )
i
i i k l
kl
l
u
Du u dx
x
(12)
Подставим выражение (12) в (11), в результате получаем:
0
i i k l
kl
du u dx
(13)
Поделим выражение (13) на ds, с учетом того что
i
i
dx
u
ds
:
2
2
0
i i l
i
kl
d x dx dx
ds ds ds
(14)
Метрический тензор.
5
Метрический тензор используется для определения длины L вдоль кривой λ
на М от точки λ (а) до точки λ (b):
1/ 2
( ( )) ( ( ))
b
i j
ij
a
dx t dx t
L g dt
dt dt
(15)
По определению (15) можно написать:
2 i j
ij
ds g dx dx
(15а)
Где
2
ds
обычно рассматривают как квадрат интервала ds между
близлежащими точками многообразия.
Т.е. квадрат элемента длины в криволинейных координатах есть
квадратичная форма дифференциалов
i
dx
.
Т.к. произведение g
ij
на контравариантный тензор
i j
dx dx
- скаляр, то g
ij
составляют ковариантный тензор, который называется метрическим.
При чем функции g
ij
являются симметричными по индексам i и j.
ij ji
g g
В частности можно сказать, что ковариантный и контравариантные
метрические тензоры являются обратными друг другу:
jk k
ij i
g g
С учетом вышесказанного и выражения (15а) метрический тензор можно
подразделить на следующие типы:
1. если det(g
ij
)
0 во всех точках многообразия, то метрический тензор
называют невырожденным (или псевдоримановым)
если квадратичная форма является положительно определенной
то тензор называют римановой метрикой
если квадратичная форма является отрицательной, то
метрический тензор называют собственно псевдоримановым (или
индефинитной метрикой)
2. если det(g
ij
)=0 в некоторых точках многообразия, то метрический
тензор называют вырожденным.
Многообразие для которого метрика является вырожденной в
любой точке называется изотропной (например, световой конус в
пространстве Минковского)
Геодезические в пространстве-времени Шварцшильда:
6
времениподобные геодезические
Уравнения геодезических в пространстве-времени с линейным элементом
2 i j
ij
ds g dx dx
(1)
могут быть получены из лагранжиана:
2
i j
ij
dx dx
L g
d d
(2)
С учетом выражения (1) лагранжиан можно переписать в виде:
2
2
ds
L
d
(3)
где τ — некоторый аффинный параметр на геодезической. В случае
времениподобных геодезических τ можно отождествить с собственным
временем s частицы, движущейся по геодезической.
Учитывая следующее выражение для метрики Шварцшильда:
2
2 2 2 2 2 2 2 2
1 sin
1
g
g
r
dr
ds c dt r d r d
r
r
r
(4)
Лагранжиан примет вид:
1
2
2 2 2 2
2 2 2 2
2 1 1 sin
g g
r r
ds
L c t r r r
d r r
1
2 2 2 2
2 2 2 2
1
1 1 sin
2
g g
r r
L c t r r r
r r
(5)
где точка означает дифференцирование по τ. Из выражения (5) можно
получить канонические импульсы, которые равны:
2
1
g
t
r
L
p c t
r
t
(7)
1
1
g
r
r
L
p r
r
r
(7а)
2 2
sin
L
p r
(7b)
2
L
p r
(7c)
Принимая во внимание выражения (7) лагранжеан можно переписать в виде:
2 ( )
t r
L p t p r p p
(8)
Из функции Лагранжа можно найти функцию Гамильтона частицы в поле по
общей формуле:
L
H p L
p
(9)
( )
t r
H p t p r p p L L
(10)
7
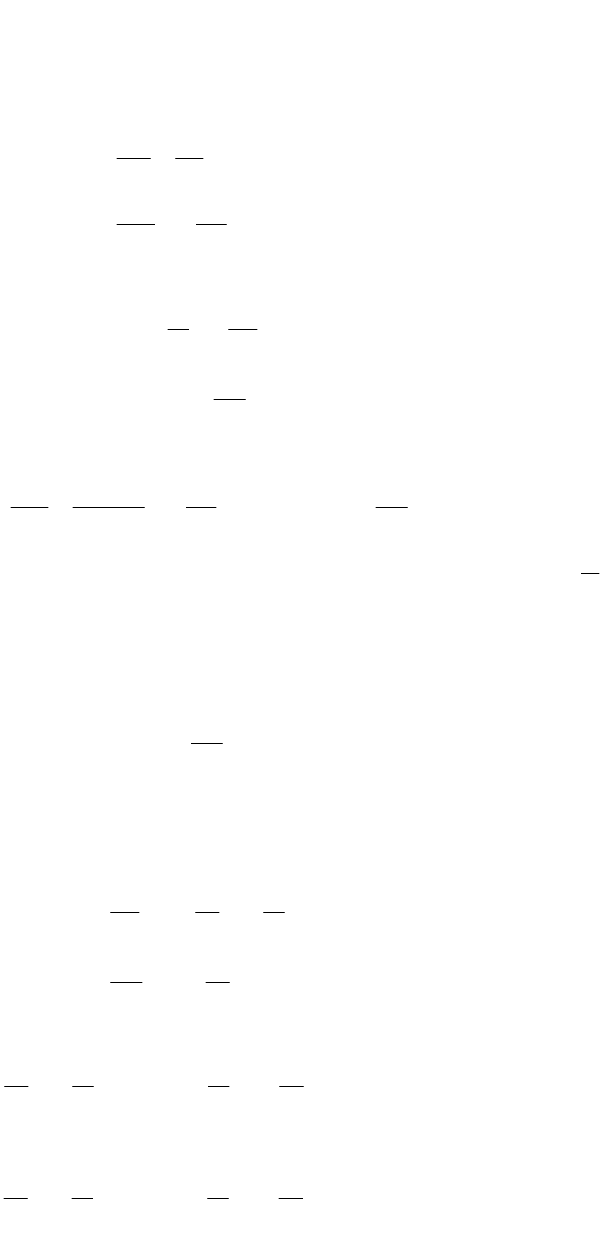
Равенство функции Лагранжа функции Гамильтона говорит о том, что полная
энергия равна «кинетической энергии». В силу той же причины
гамильтониан и лагранжиан постоянны:
H L const
(11)
Меняя масштаб аффинного параметра τ, можно сделать 2L=+1 для
времениподобных геодезических или 0 для изотропных геодезических.
Другие интегралы движения получаются из уравнений
0
t
dp
L
d t
(12)
0
dp
L
d
(13)
Из выражений (7), (7b), (12), и (13) следует:
2
1
g
t
r
dt
p c const E
r d
(14)
2 2
sin
d
p r const
d
(15)
Кроме того, из уравнения движения
2
2
2
( )
sin cos
dp
d r L d
r
d d d
(16)
следует, что если выбрать начало отсчета угла
так, чтобы
2
(соответственно
0
), то. θ в этом случае остается постоянным в процессе
движения и все геодезические будут лежать в экваториальной плоскости.
Уравнение (15) теперь принимает вид
2
d
p r const l
d
(17)
где l — момент количества движения относительно оси, перпендикулярной
плоскости экватора.
Подставляя в функцию Лагранжа значения уравнения:
1
2
1
g
r
dt E
t
d c r
(14а)
2
d l
d r
(17а)
Получаем:
1 1
2
2 2
1 1 2 1
g g
r r
E l
r L
c r r r
(18а)
(для времениподобных геодезических) и
1 1
2
2 2
1 1 2 0
g g
r r
E l
r L
c r r r
(18b)
(для изотропных геодезических).
В случае же времениподобных геодезических уравнения (17) и (18) могут
быть переписаны следующим образом:
8
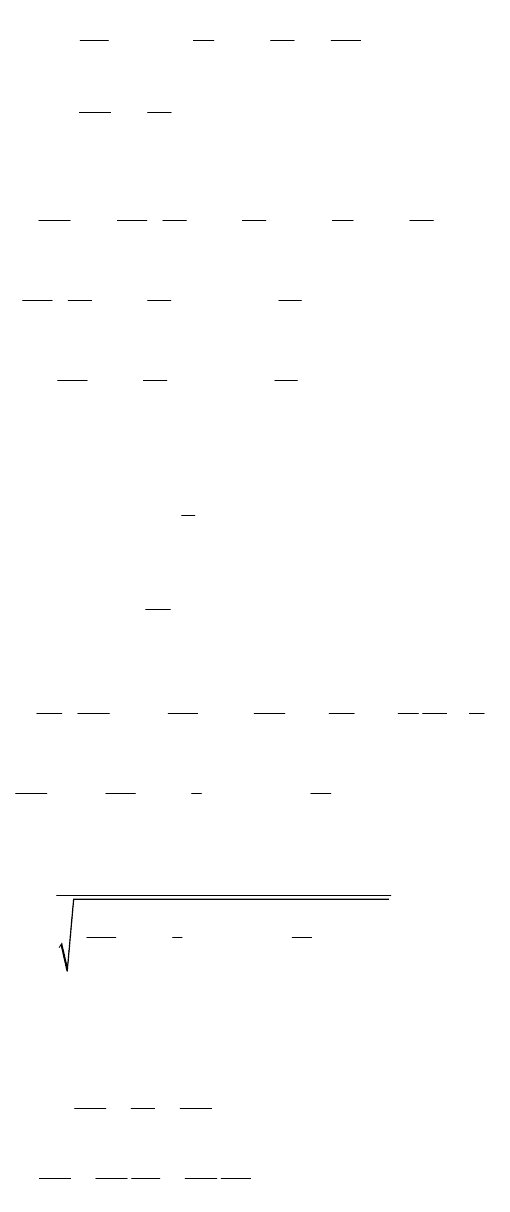
2
2 2
2 2
1 1
g
r
dr l E
d r r c
(19a)
2
d l
d r
(19b)
Совмещая уравнения (19a) и (19b) получаем:
2 2
2
2 2 2 2
2 2
1 1
g
r
dr E r r l
d c l l r r
2 2
2 2 2 3
2
2 2
g g
E r r r
r r rr
c l l l
(20)
2
2 2 3
2
2 2
1
g g
E r r
r r rr
c l l
Сделаем следующую замену,
1
u
r
(21)
Тогда
2
1
du dr
u
(22)
Произведя замену, получаем:
2
2
2
4 2 2 2 2 3
1 1 1 1 1 1
1
g g
du E
r r
u d c u l u l u u
2
2
2
2 3
2 2
1 1
1
g g
du E
u r u u r
d c l l
(23)
2
2
2 3
2 2
1 1
1
g g
du
d
E
u r u u r
c l l
(24)
Уравнение (24) определяет геометрию геодезических в экваториальной
плоскости. Если известно решение уравнения (24) φ(u), то окончательное
решение получается в квадратурах прямым интегрированием уравнений
2
2
1d r
d l lu
(25)
2
1
2 2
1
1
g
dt d dt E
r u
d d d lu c
(26)
9
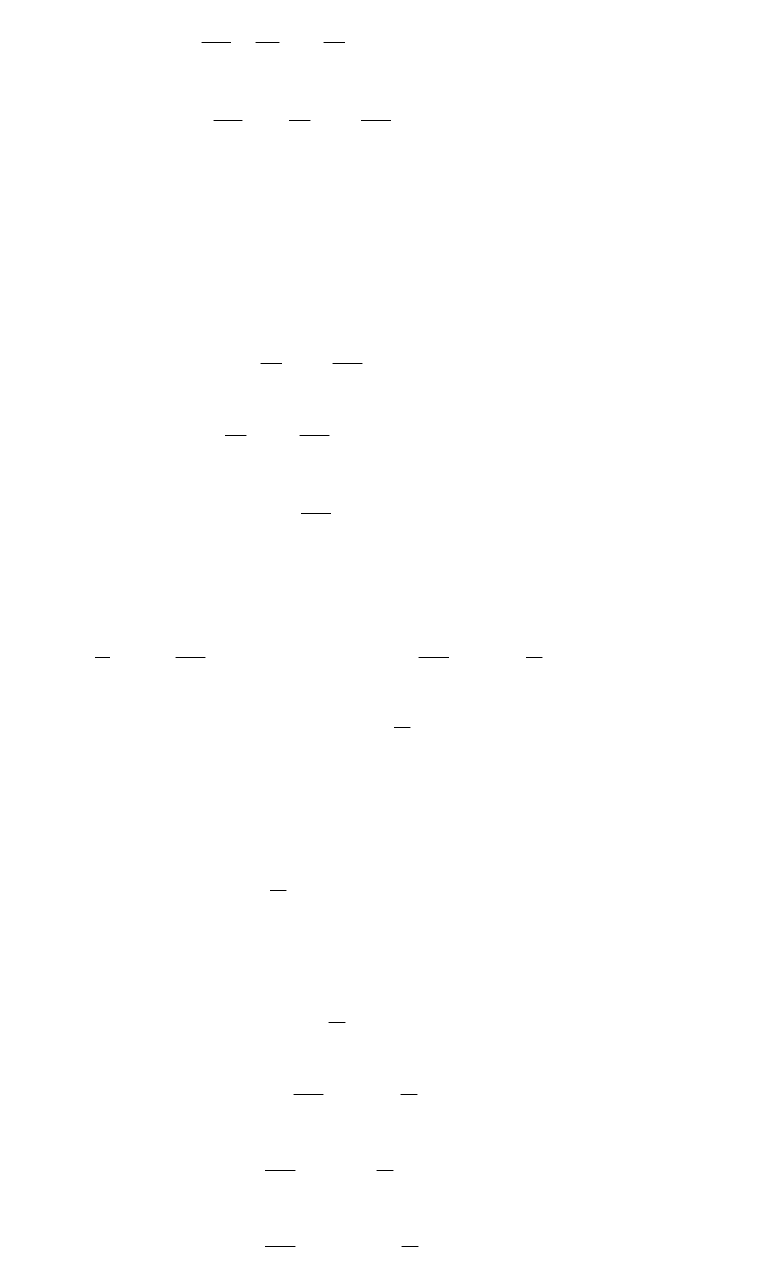
Радиальные геодезические.
Радиальные геодезические для частиц обладающих нулевым моментом
количества движения иллюстрируют, свойства пространства-времени.
Уравнения этих геодезических имеют следующий вид (аналоги формул (14)и
(19а)):
1
2
1
g
r
dt E
d c r
(27)
2
2
2
1
g
r
dr E
d r c
(28)
Рассмотрим траектории частиц, которые начинают движение из состояния
покоя на некотором конечном расстоянии r
i
и падают к центру. Начальное
расстояние связано с постоянной интегрирования Е соотношением (28) при
условии
i
r r
(
0r
):
2
2
0 1
g
i
r
E
r c
2
2
1
g
i
r
E
r c
1
2
2
1
i g
E
r r
c
(29)
Уравнения движения (29) можно проинтегрировать, введя переменную
,
такую что:
1 1
2 2
2
2 2
1
1 cos 1 1 cos
2 2
g g
E E
r r r
c c
(30)
2
cos
2
i
r
Из выражения (30) следует, что:
при
i
r r
(т.е. когда частица находится на конечном расстоянии от
горизонта)
2
cos 1
2
0
, (31)
При
g
r r
(т.е. когда частица пересекает горизонт)
2
cos
2
g i
r r
1
2
2
2
1 cos
2
g g
E
r r
c
2
2
2
1 cos
2
E
c
2
2
2
1 1 sin
2
E
c
10
