Геловани В.А. и др. Интеллектуальные системы поддержки принятия решений в нештатных ситуациях

Подождите немного. Документ загружается.

3.2. Формализация поиска решения 81

• используя понятие рекурсивной функции (с предварительным введе-

нием понятия вычислимой функции) (работы Гильберта

Д.,

Геделя К.,

Черча А , Клини С, Поста Е., Маркова

А.

А.);

• используя описание точно определенного класса процессов, совер-

шаемых соответствующим образом устроенными «машинами» (рабо-

ты Поста Е., Тьюринга А., фон Неймана Д.).

Была доказана равносильность всех предложенных уточнений в том

смысле, что все они приводят в результате к одному и тому же классу

вычислимых функций.

В качестве одного из средств для уточнения интуитивного поня-

тия алгоритма будем рассматривать продукционные системы (модели),

активно используемые как средство формализации эвристической (экс-

пертной) информации в интеллектуальных системах и, в частности,

системах поддержки принятия решений. Продукционные модели по-

зволяют реализовать как детерминированную (алгоритмическую) схему

вычислений, так и схему вычислений, содержащую элементы недетер-

минизма. Последнее свойство собственно и отличает продукционные

модели от классических алгоритмических схем с присущими им последо-

вательностью и детерминизмом и делает их довольно удобным средством

представления (формализации) плохоформализуемой и слабоструктури-

рованной информации.

Продукционные модели представления знаний с присущей им де-

кларативностью (как отмечается в [79], продукционные системы явля-

ются наиболее декларативным способом представления знаний среди

процедурных моделей и наиболее процедурным способом среди декла-

ративных, — последнее подразумевает относительную простоту задания

процедуры обработки продукционных правил при поиске решения) обла-

дают следующими основными достоинствами:

• универсальность (независимость от ПО) представления знаний с до-

вольно простой формой их выражения;

• естественная модульность продукционных моделей, каждая продук-

ция представляет собой, как правило, законченный фрагмент зна-

ний, что обеспечивает простоту модификации модели; однако при

необходимости все множество продукций легко может быть струюу-

рировано путем разбиения на подмножества семантически близких

продукций, соответствующих отдельным фрагментам ПО;

• недетерминированность, асинхронность и естественный параллелизм

продукционных моделей, позволяющие реализовывать на их основе

профаммные системы, ориентированные на высокопроизводитель-

ные параллельные вычислительные комплексы, в том числе с нетра-

диционной (отличной от неймановской) архитектурой, в частности

архитектурой «потока данных».

Основные недостатки продукционных моделей следующие:

• сложность контроля «правильности» (корректности) продукционных

моде.чей, что характерно для всех недетерминированных систем;

82 Бтава 3. Методы поиска решений для динамических баз знаний

• относительно невысокая эффективность получаемой программы по

сравнению с использованием традиционных процедурных систем

(языков) программирования.

Первый недостаток, как отмечается в [79], имеет и свою положитель-

ную сторону, заставляя выносить вопросы корректности продукционной

модели на самый высокий уровень — уровень представления знаний.

На этом уровне активно работает эксперт и проблема корректности реша-

ется с существенно меньшими трудозатратами, чем когда она «опустится»

на уровень сгенерированной программы.

Относительно второго недостатка заметим, что с развитием непроце-

дурного, декларативного стиля программирования, в частности продук-

ционного и функционального, и вычислительных систем, поддерживаю-

щих этот стиль (например потоковых ЭВМ), различие в эффективности

получаемых программ все более уменьшается.

3.2.4. Анализ продукционных систем

3.2.4.1.

Алгоритмический подход

Продукционные системы (модели) будем рассматривать с точки зре-

ния формальных систем [71, 103]. Следуя [71], формальная система

определяется своим алфавитом А = {а,}, г =

т, и конечной сово-

купностью «правил вывода» Pj,...,P„. Под i-местным правилом вы-

вода Р, при этом понимается некоторое рекурсивное множество i-ок

(а;1,...,Ж;) слов в алфавите А. Данное множество обычно задается

некоторым «простым» правилом, позволяюшлм для любой произволь-

но взятой Z-ки слов узнать, обладает она соответствующим признаком

или нет.

Слово и называется непосредственным следствием из некоторой

совокупности слов V (обозначается U = и), если возможно указать такое

правило вывода Р, и такие слова

Х\,...

,xi в U, что последовательность

{xi,... ,Xi,u) принадлежит Р,.

Слово и называется следствием из совокупности слов U, или выво-

димо из и (в данной формальной системе) (обозначается U

—

и), если

можно указать такую конечную последовательность слов (a;i,..., ж;), что

и = xi, {и,

Ж]}

= Х2,..., {и, Xi,..., xi}

—

и. Дополнительно полагается,

что каждое слово есть непосредственное следствие самого себя, т. е., если

и С и,

то

и = и.

Формальным доказательством на основе некоторой совокупности

слов и формальной системы F называется любая конечная последо-

вательность слов (xi,X2, ••. ,Xt) из F, обладающая свойством для ка-

ждого X,, О < г < t, или X си, или {х\,Х2,... ,Xt} = х. Последнее

слово X формального доказательства называется его утверждением, а все

формальное доказательство {х\,Х2,... ,xt) называется формальным вы-

водом X из {ж} на основе U.

Из определения формальной выводимости непосредственно вытека-

ют следующие ее свойства:

1) если и

—

uuU

—

W,ToW

—

и;

2) если и

—

и и {и, и}

—

W,TOU

- w;

3.2. Формализация поиска решения 83

3) если слово и выводимо из некоторой бесконечной совокупности

слов и, то и выводимо из некоторой конечной совокупности U' CU.

Справедлива следующая теорема |71j.

Теорема.

Пусть

— некоторая фзрмальная система

— некоторое

рекурсивно

перечислимое

множество слов в F. Тогда совокупность

всех

формальных доказательств

в F на основе U также рекурсивно

перечислима.

Выделенное рекурсивно перечислимое множество U называется мно-

жеством аксиом формальной системы F. Иногда интересуют лишь слова

определенного, правильного в каком-то смысле вида. Такие

с;гова

на-

зываются формулами (или правильно построенными формулами), а вы-

водимые формулы называются теоремами рассматриваемой формальной

системы F. Для графического представления вывода используется дерево

вывода

(103].

Рассмотрим подстановочные и продукционные системы, предста-

вляющие собой формальные системы специального вида [60, 71, 73, 75,

ПО,

171].

Подстановочная система i^ [71] определяется некоторым алфавитом

А = {а}, i = 1,7П, и конечной системой Р базисных подстановок

{х-^у},

г = 1,п, (3.1)

где X, у — некоторые (возможно пустые) слова (цепочки) в алфавите А.

Подстановка х

—>

у понимается как правило вывода Р,, предполагая,

что Р,{и, ад) истинно, если слово w получается из слова и посредством

подстановки в и слова у вместо какого-либо вхождения слова х.

Слово

в алфавите А называется заключительным в подстановочной

системе F, если ни одна из подстановок из Р не применима к ад (т. е.

ни одно из

не входит в ад). Слово и перерабатывается в слово

ад

посред-

ством подстановочной системы, если и

—

ад

является заключительным

словом. В ситуации, когда для каждого слова и из некоторого рекурсив-

ного множества U существует не более одного заключительного слова ад,

удовлетворяющего соотношению и

—

ад,

имеем частичную функцию на U,

вычислимую системой F. Так как множество пар слов {«, ад}, удовле-

творяющих соотношению и - w, рекурсивно перечислимо (напомним,

что в любой формальной системе совокупность слов, выводимых из про-

извольного рекурсивно перечислимого множества, является рекурсивно

перечислимой), а множество всех заключительных слов рекурсивно, то

введенная функция является частично рекурсивной.

Подстановочная система в том виде, как она оггределена, является

«максимально недетерминированной» в том смысле, что допустим про-

извол как в выборе заменяемого вхождения слова х в и, если такое

вхождение не единственно, так и в выборе собственно применяемой

подстановки, если таких подстановок, применимых к и несколько (на-

пример, в Р имеются подстановки х

—»

у и а;

—>•

г). Таким образом,

подстановочная система не соответствует алгоритмической схеме, так как

не выполняется свойство детерминированности.

84 Глава 3. Методы поиска решений для динамических баз знаний

Шагом к большей определенности является использование продук-

ционной (канонической или нормальной) системы Поста Т [60, 71, 171],

задаваемой конечным алфавитом А = {а}, г = 1,т, и конечной систе-

мой Р базисных продукций типа (для нормальной системы)

{xW-^Wy},

= 1,71, (3.2)

где X, у ~ некоторые слова в алфавите А.

Для нормальной системы определено правило выбора заменяемого

вхождения. Так применение продукции xW

—*

Wy к некоторому слову и

означает вычеркивание начального вхождения х в слово и и последующее

приписывание к оставшемуся слову слова у.

Продукционную систему (ПС) можно рассматривать как формаль-

ную систему с правилами вывода Р,, i = 1,п, где P,(u,w) считается

истинным, если слово w получается из слова и при помощи продук-

ции xW

—+

Wy.

Доказана теорема (см., например,

[71 ])

о том, что для любой заданной

подстановочной системы F с алфавитом А и системой подстановок (1.2)

можно построить ПС Т, такую, что будет справедливо следующее утвер-

ждение: для любых двух слов и,

в алфавите А отношение u

—

w истинно

в системе подстановок F тогда и только тогда, когда оно истинно в ПС Т.

Поэтому далее будем использовать название «продукционная систе-

ма» и к системе типа (1.2) и к системе типа (1.3).

Важным является следствие из приведенной теоремы о том, что

существует такая ПС Г, в которой совокупность всех слов, выводимых

из подходящего фиксированного слова и, является нерекурсивной.

Вообще с ПС (любого типа) Пост связал следующие две основные

алгоритмические проблемы:

• Проблема остановки: рекурсивна или нет совокупность всех тех слов,

начиная с которых процесс вывода обрывается через конечное число

шагов?

• Проблема выводимости: для каждого ли слова и является рекур-

сивной совокупности всех тех слов, которые можно получить из и

конечным числом продукций.

Пост показал, что существуют такие ПС, для которых обе проблемы

имеют отрицательное решение.

Дальнейшим шагом по «снятию недетерминизма» и приближению

к алгоритмической (детерминированной) схеме являются однородные

(или глоногенные) продукционные системы [60] и нормальные алго-

ритмы [73, 74], в которых снимается неопределенность неоднозначного

выбора применимых продукций.

В однородной системе множество продукций Р удовлетворяет тре-

бованию, что к любому данному слову и применимо не более одной

продукции из Р. Однородная система функционирует подобно последо-

вательной машине. Доказана аналогичная предыдущей теорема о возмож-

ности построения для продукционной системы Г однородной системы Т'

и наоборот.

3.2. Формализация поиска решения 85

Полностью детерминированной является алгоритмическая схема

ви-

де нормального алгоритма Маркова, задаваемого алфавитом А и конечной

системой Р продукционных правил

[x^yj, i=\,n,

некоторые из которых помечены как заключительные. Конечная последо-

вательность продукций Р называется схемой. Для нормального алгоритма

определены следующие правила выбора и замещения:

• продукции из Р просматриваются последовательно по списку;

• если к входному слову и применимо более одной продукции из Р,

то применяется первая по списку;

• если слово X входит в качестве полслова более одного раза в слово и,

то у замещает первое (самое левое) вхождение а; в и;

• процесс останавливается, давая в результате слово w, когда при-

меняется заключительная продукция или когда никакая продукция

из Р уже не применима к и (тогда w = и). Если результат полу-

чается на п-и шаге, то считается, что процесс переработки слова

обрывается после п-го шага. Если процесс переработки слова и про-

должается бесконечно, то считается, что результат переработки слова

и посредством данного алгоритма не определен.

Таким образом определяется вычислимая по нормальному алгоритму

функция f: А

—>•

А', где А' — множество слов в алфавите А. Доказано,

что функция / вычислима по алгоритму Маркова тогда и только тогда,

когда / вычислима посредством продукционной системы Поста.

Итак, мы рассмотрели ветвь, ведущую к детерминированной, «алго-

ритмической» концепции ПС. Именно эта концепция является в насто-

ящее время доминирующей в системах продукционного программирова-

ния. Она принята за основу в продукционных языках типа РЕФАЛ [12],

OPS

[153],

Пролог [62], Пилот [117] (в Пилоте имеется также механизм

случайного выбора из «конфликтного множества»). Однако данная кон-

цепция плохо согласуется с представлением эвристических, недетермини-

рованных знаний. Известны подходы к «увеличению недетерминизма»,

базирующиеся на использовании трансфинитных формальных систем,

в частности уже упоминавщихся ПС с исключениями из правил для пред-

ставления неформальных процедур, использованной в /J"-системе продук-

ционного программирования [64], и системы алфавитных операторов [25].

Рассмотрим данную проблему в общем виде, т. е. проанализируем

возможности реализации недетерминизма в ПС, используя исчисленчес-

кую (диспозиционную) схему.

3.2.4.2.

Диспозиционный подход

В [26] введено формальное определение понятия диспозиции, явля-

ющееся в определенном смысле обобщением понятия алгоритма. Всякая

экспликация понятия алгоритма сводится по сути к экспликации сле-

дующих трех понятий: понятия текста, т. е. совокупности слов, над ко-

торыми производятся преобразования; понятия правил преобразований

86 Глава 3. Методы поиска решений для динамических баз знаний

текста (в нашем случае это продукционные правила), т.

е.

описания того,

как выполняются эти преобразования; и понятия схемы алгоритма, т. е.

конечной совокупности правил и способа (стратегии) задания порядка

выполнения этих правил. Алгоритм считается применимым к некоторой

совокупности слов и, если определенный алгоритмом процесс после-

довательных применений преобразований заканчивается через конечное

число шагов.

Характерным примером алгоритма, как отмечалось, является нор-

мальный алгоритм Маркова, определенный конечным множеством пере-

нумерованных отрезком натурального ряда продукционных гфавил, неко-

торые из которых объявлены заключительными, и стратегией, задающей

каждый раз выбор продукции с наименьшим номером из применимых

к данному слову. Алгоритм заканчивает свою работу, если выполнена

одна из заключительных продукций или если ни одна из продукций

не применима к данному слову.

Наряду с понятием алгоритма, в математике используется понятие

исчисления. Исчисления, как и алгоритмы, оперируют с текстами, под

которыми понимаются исходные и выводимые в данном исчислении

формулы В исчислениях также производятся преобразования текстов

по некоторым правилам (правилам вывода), число которых фиксировано

для каждого исчисления. Однако, в отличие от алгоритма, в исчислении

нет понятия, аналогичного понятию схемы алгоритма, и по другому

трактуется понятие результата.

В исчислении к любому исходному тексту (исходной формуле) разре-

шается применять любое правило вывода, применимое к данному тексту.

К полученному тексту (формуле) опять разрешается применять любое

правило и т.

д.

Исчисление позволяет получить множество текстов-, вы-

водимых из исходного текста, а алгоритм получает по исходному тексту

однозначно определенный результирующий текст.

Различие между алгоритмом и исчислением сводится по существу

к различию модальностей, определяющих стратегии применения преобра-

зований над текстами. Для алгоритмических схем используется модаль-

ность предписания (необходимости), а для исчисления — модальность

разрешения. Заметим, что поскольку для ПС не определена стратегия вы-

бора применимых продукционных правил, то предложенные Э. Постом

нормальные системы [171] А.А.Марков исследовал как ассоциативные

исчисления (нормальные исчисления Поста) [73], в которых разрешено

последовательно выполнять подходящие продукционные правила из не-

которойконечной совокупности правил над заданными исходными сло-

вами, в частности исходным словом) в заданном алфавите.

При описании методов решения многих задач на ЭВМ, в осо-

бенности плохоформализуемых задач искусственного интеллекта, часто

удобнее использовать обе модальности. Схемы описания задач (мето-

дов их решения), в которых кроме предписаний выполнять некоторые

преобразования текстов по некоторым правилам, используются также

разрешения выполнять некоторые преобразования, называются диспози-

циями. Основной в диспозиции является именно модальность разреше-

ния, но при этом используется и модальность предписания.

3.2. Формализация поиска решения 87

Следуя [26, 73], используем «классическое» понятие алгоритма с от-

меченными ранее свойствами дискретности, детерминированности, эле-

ментарности шагов, направленности и массовости, хотя в научной ли-

тературе (см., например, [65, 70]) используется понятие недетермини-

рованного алгоритма и недетерминированной машины Тьюринга, до-

пускающих неоднозначный выбор преобразований в смысле, что если

разрешено выполнять какие-то преобразования, то подразумевается, что

одно из этих преобразований должно быть вьшолнено на следуюш;ем

шаге. Предписание также можно интерпретировать как вырожденный

случай разрешения, когда разрешается только одно преобразование.

Отличие диспозиции от алгоритма состоит в том, что диспозиция

может иметь множество реализаций. При этом возможно получение или

всех возможных алгоритмов по данной диспозиции или хотя бы одного

из них.

Формально диспозиция D задается алфавитом А, множеством (ко-

нечным) правил преобразований Р и стратегией применения правил

в виде фафа диспозиции. Графом диспозиции G{D) называется связный

граф,

вершинам которого сопоставлены правила преобразований или

некоторый специальный знак, удовлетворяюш;ий следующим свойствам:

• имеется только одна вершина, называемая входом диспозиции и обо-

значаемая а„;

• имеется по крайней мере одна вершина, из которой не исходит ни од-

на дуга и которой сопоставлен специальный знак. Такие вершины

называются выходами диспозиции и обозначаются

a^i,...,

%*!

• вершинам, не являющимся выходами, сопоставлены правила пре-

образований (некоторые правила могут быть сопоставлены несколь-

ким различным вершинам). Каждый выход правила Р, сопоставляет-

ся одной из дуг, выходящих из соответствующей вершины а,; каждой

дуге,

исходящей из а,, должен быть сопоставлен по крайней мере

один из выходов правила Р,.

Граф диспозиции является по сути деревом вывода, или решающим

деревом.

Диспозиция D называется правильной (корректной), если, кроме

вышеперечисленных, удовлетворяются также следующие дополнительные

свойства:

• из любой вершины графа G{D) существует путь по крайней мере

в один выход;

• для каждой вершины графа G{D) существует путь, ведущий из входа

в эту вершину.

Диспозиция называется однозначной, если каждому исходному тек-

сту соответствует единственный результат, и алгоритмической, если для

любого исходного текста на каждом шаге преобразования возможен (а сле-

довательно, и предписан) переход только к одной вершине графа G{D).

Нетрудно заметить, что алгоритмической диспозиции соответствует од-

нородная продукционная система.

88 Глава 3. Методы поиска решений для динамических баз знаний

Важную роль играет понятие реализации диспозиции. Формально

реализация диспозиции определяется следующим образом.

В графе G(D) рассматриваются пути, состоящие из последователь-

ности вершин (а,,..., ojv), где а, = а„, адг =

OR.

Так как в графе G(D)

каждой вершине о,, кроме выходных, сопоставлено правило преобразова-

ний

Ргг,

ТО

каждому такому пути будет сопоставлена последовательность

правил (Рг.,

• •

•,

Ртм)-

Пусть правило Р„, сопоставленное вершине а,, применимо к ис-

ходному (начальному) тексту

UQ,

а каждое правило Рг, преобразует текст

и, — в CTj. Тогда, если в последовательности правил после применения

каждого правила Р^, к тексту U, — возможно применение правила Prj

к тексту Uj, то данная последовательность правил и соответствующая

ей последовательность текстов

(Uo,U,,...

,Uk) называется реализацией

диспозиции D, а заключительный текст Щ — результатом применения

диспозиции D к исходному тексту Щ.

Последовательность правил преобразований и текстов, соответству-

ющих некоторой реализации диспозиции D, можно представить после-

довательностью (цепочкой) переходов вида

Так как для некоторого исходного текста Щ может существовать мно-

жество возможных реализаций, то вводится понятие эквивалентности

реализаций. Реализации называются эквивалентными, если у них совпа-

дают исходные и конечные тексты. Если для текста Щ не существует

ни одной реализации, то считается, что данная диспозиция D непри-

менима к

UQ.

Случай безрезультатной остановки не рассматривается

как реализация диспозиции. Заметим, что введение данного отношения

эквивалентности на множестве реализаций, позволяет рассматривать дис-

позицию как формальную (продукционную) систему, удовлетворяющую

свойству Черча—Россера

[126].

Следовательно, для однозначной диспозиции для некоторого исход-

ного текста, хотя и возможно несколько различных реализаций, но все

они эквивалентны. Для алгоритмической диспозиции, если преобра-

зования текста определены однозначно, для всякого исходного текста

существует не более одной реализации.

Обозначим множество результатов применения диспозиции D к тек-

сту и как R(D, и). Возможны следующие постановки задачи нахождения

результата применения диспозиции D к тексту U:

• нахождение всех результатов (если R{D, U) конечно);

• нахождение хотя бы одного результата;

• нахождение данного результата оптимальным (или допустимым)

в определенном смысле образом;

• решение вопроса о существовании и (или) единственности резуль-

тата.

3.2. Формализация поиска решения 89

Рассматривая диспозиции в контексте формальных систем можно

доказать, что [26]:

• существуют диспозиции, для которых R{D, U) бесконечно;

• существуют диспозиции, для которых задача о принадлежности не-

которого текста U' к множеству R{D, U) является алгоритмически

неразрешимой;

• можно выделить класс диспозиций, для которых множество R{D, U)

конечно при любом тексте U из области возможных исходных дан-

ных.

Подытоживая данный параграф, отметим основные преимущества

выбора диспозиции перед алгоритмом как средства описания метода

решения плохоформализуемых, недетерминированных задач, или как

средства задания МПР:

• возможна формализация метода поиска решения в случае, когда

построение (или выбор) алгоритма решения невозможно из-за от-

сутствия информации; с получением необходимой информации воз-

можен переход от диспозиции к алгоритму поиска решения;

• по описанию метода поиска решения в виде диспозиции может быть

получен ряд различных алгоритмов поиска решения, из которых

в дальнейшем может быть выбран наиболее эффективный;

• в условиях недетерминизма можно ставить и исследовать задачу по-

лучения всех реализаций или всего множества результатов R{D, U)

(в случае его конечности), или некоторого ограниченного подмно-

жества результатов, причем процесс получения результатов можно

распараллелить.

Учитьшая вышеизложенное, будем рассматривать продукционную

систему как диспозицию.

3.2.4.3.

Анализ

результата.

Связь

задачей принятия решений

Рассмотрим следующую задачу. Пусть имеется некоторая ПС F,

заданная своим алфавитом А = {а}, г = 1,т, и конечным набором

продукционньЕх правил Р. Имеется некоторая начальная совокупность

слов (текст) Щ. Требуется найти сово1супность всех тех слов (тек-

стов) R(F,

UQ),

которые могут быть получены из fb посредством продук-

ций из р.

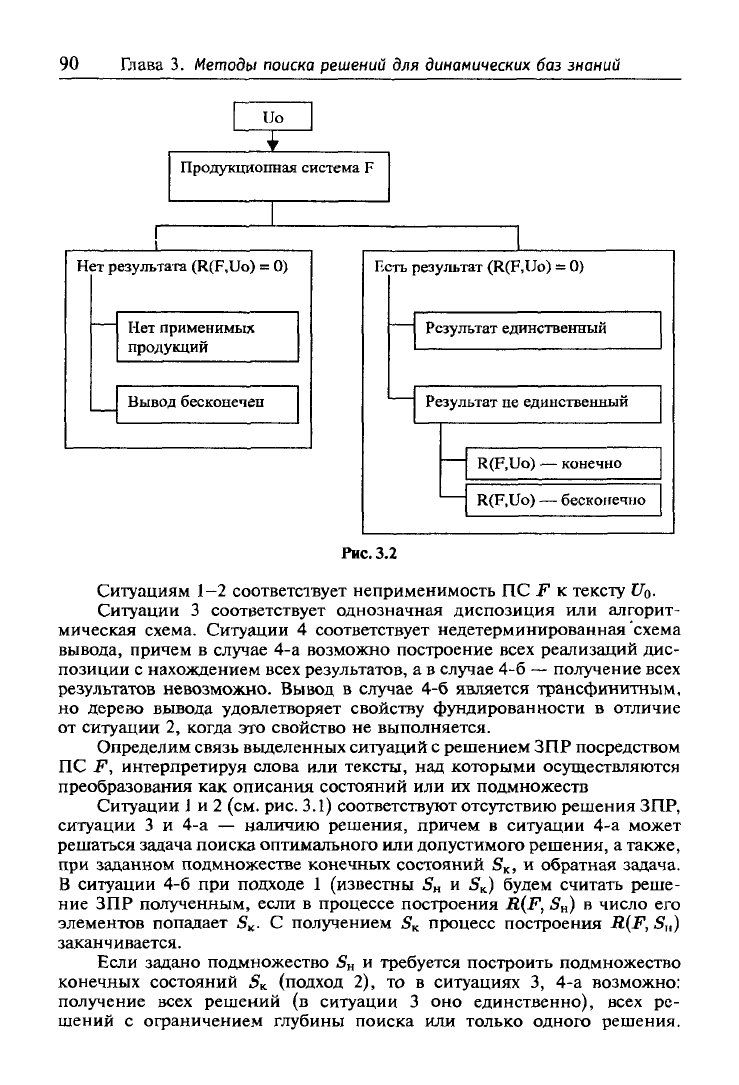
Интерпретируя ПС в общем виде как диспозицию и учитывая про-

веденный ранее анализ, можно выделить следующие ситуации (рис. 3.2):

1) продукции из Р неприменимы к J7o;

2) вывод бесконечен;

3) результат единственный, т. е. множество R{F,

UQ)

состоит из одного

элемента;

4) результат не единственный:

а) R(F,

Ua)

конечно;

б) RiF,

UQ)

бесконечно.

Diaea 3. Memodbi поиска решений для динамических баз знаний

Продукционная система F

Нет

результата (R(F,Uo)

Нет применимых

продукций

Вывод бесконечен

Есть

результат (R(F,Uo)

Результат единственный

Результат

не

единственный

R(F,Uo)

—

конечно

R(F,Uo)

—

6ecK0tie4HO

Рис.

3.2

Ситуациям 1-2 соответствует неприменимость ПС F к тексту Щ.

Ситуации 3 соответствует однозначная диспозиция или алгорит-

мическая схема. Ситуации 4 соответствует недетерминированная'схема

вывода, причем в случае 4-а возможно построение всех реализаций дис-

позиции с нахождением всех результатов, а в случае 4-6

—

получение всех

результатов невозможно. Вывод в случае 4-6 является трансфинитным,

но дерево вьшода удовлетворяет свойству фундированности в отличие

от ситуации 2, когда это свойство не выполняется.

Определим связь выделенных ситуаций

решением ЗПР посредством

ПС F, интерпретируя слова или тексты, над которыми осуществляются

преобразования как описания состояний или их подмножеств

Ситуации J и 2 (см. рис. 3.1) соответствуют отсутствию решения ЗПР,

ситуации 3 и 4-а — наличию решения, причем в ситуации 4-а может

решаться задача поиска оптимального или допустимого решения,

также,

при заданном подмножестве конечных состояний S^, и обратная задача.

В ситуации 4-6 при подходе 1 (известны S„ и 5^) будем считать реше-

ние ЗПР полученным, если в процессе построения R{F, S„) в число его

элементов попадает 5^. С получением S^ процесс построения R{F, S„)

заканчивается.

Если задано подмножество 5н и требуется построить подмножество

конечных состояний 5к (подход 2), то в ситуациях 3, 4-а возможно:

получение всех решений (в ситуации 3 оно единственно), всех ре-

шений с ограничением глубины поиска или только одного решения.