Гайдамакин Н.А. Автоматизированные информационные системы, базы и банки данных. Вводный курс Учебное пособие

Подождите немного. Документ загружается.

6.4. Гипертекстовые информационно-поисковые системы

тателя по гиперссылкам. «Щелкнув» мышью по выделенному

слову (т. е. по гиперссьшке), пользователь-читатель открывает

связанный по ссылке текст (другой фрагмент этого же текста

или другой текст).

Привычным «бумажным» аналогом гипертекста являются

оглавления и предметные указатели книг, содержащие ссылки

на главы, разделы или фрагменты книги с соответствующей

информацией. При этом ссылка выглядит как номер страницы,

с которой начинается соответствующая глава или раздел, где

находится соответствующий фрагмент текста. Отобрав в оглав-

лении или предметном указателе нужное название или термин

и считав номер соответствующей страницы, читатель открыва-

ет книгу в искомом месте, т. е. переходит, или, выражаясь по-

другому, осуществляет «навигацию» в нужное место книги.

В 70-е и 80-е годы, в особенности в период «персонализа-

ции» вычислительной техники, бьши предприняты многочис-

ленные попытки создания специальных гипертекстовых обо-

лочек, на основе которых либо совершенствовался примитив-

ный текстово-командный интерфейс ранних операционных

систем (знаменитая оболочка

«Ног1оп

Соттапс1ег»

для ОС

М5

В05),

либо для прикладных программных средств созда-

вались гипертекстовые справочные (11е1р-овые) системы и ру-

ководства.

В конце 80-х — начале 90-х годов были предприняты пер-

вые попытки стандартизации гипертекста. Таким стандартом

являлся стандарт

Атег1сап

СуЬегпеисх

НуреПех!

5у8(;ет (АС1

НуреПех!),

реализованный в среде встроенной системы макро-

команд широко известного в «узких» программистских кругах

текстового редактора

МиШЕс11(; .

Впоследствии гипертекст стал широко использоваться в

справочных системах программ-приложений операционной си-

стемы \У1пс1о\У8 и фирмой

МюгоЗой

был разработан специаль-

ный пакет \У1пНе1р для создания гипертекстовых справочных

«систем помощи». В настоящее время техника гипертекста яв-

ляется фактическим стандартом создания разнообразных ком-

281

Документальные

информационные системы

пыотерных справочных и учебных систем, руководств пользо-

вателя и энциклопедий.

Период взрывной интенсификации применения технологий

гипертекста связан с бурным развитием и распространением в

конце 80-х — начале 90-х годов глобальных информационных

систем, и, в частности, сети Интернет. Идеи гипертекста как

принципа ассоциативного связывания в распределенную инфор-

мационную среду документов на территориально удаленных

компьютерах были использованы группой специалистов под

руководством Теодора Нельсона, который в

1988

г. представил

проект гипертекстовой системы Хапас1и, финансировавшийся

впоследствии основателем известной компании

Аи1ос1е5к;

Джо-

ном Уокером, который в то время пророчески предвещал все-

объемлющее развитие и распространение гипертекстовых тех-

нологий. В 1989 г. в Лаборатории физики элементарных частиц

европейского центра ядерных исследований (ЦЕРН) под руко-

водством Тима Бернерса-Ли стартовал проект создания гипер-

текстовой системы обмена научными данными в сети Интер-

нет, получивший впоследствии название «Всемирной паути-

ны» —

\Уог1(1-\У1(1е

\УеЬ

(\У\У\У).

В 90-х годах паутина

\У\У\У

стала одним из наиболее бурно развивающихся сегментов сети

Интернет,

создав немыслимую ранее глобальную гипертексто-

вую информационную инфраструктуру.

6.4.2. Структура, принципы построения

и использования гипертекстовых ИПС

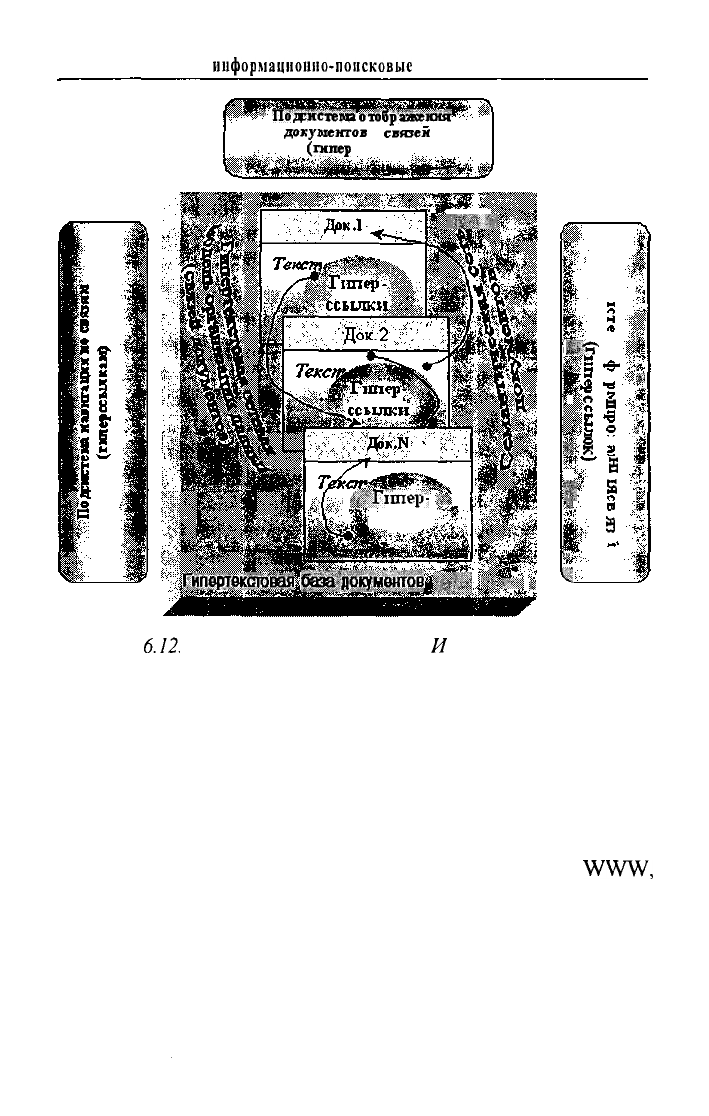
В структуре гипертекстовой ИПС можно выделить не-

сколько функциональных подсистем (см. рис.

6.12).

Основными из них являются:

• подсистема

отображения документов и гиперссылок;

• подсистема

навигации по связям (гиперссылкам);

• подсистема

формирования связей (гиперссылок);

• и

собственно сама гипертекстовая база (хранилище) до-

кументов.

Подсистема

отобра:нсеи11я

документов

гиперссылок

(гипертекста) базируется на принципах отображения докумен-

282

6.4, Гипертекстовые

ииформацноипо-попсковые

системы

Подехстепа отображехшт

дохушентов

слязея

(тхпер

ссылок)

••щл^ь

>>4.'Г1ше1)-

/Г<

ссылки

|и,-=Г I

г >

«•;

=1 -

(в

я, •

Гипортексгавая

6аза'||о1(ум№тов

'г^>^

«-;

Рис.

6.12.

Структура гипертекстовой

ПС

тов в текстовых редакторах (страницы, поля, абзацы, шрифт,

скроллинг и т. д.) с дополнительными приемами внешнего ото-

бражения в тексте гиперссылок. Как уже отмечалось, стандар-

тным способом отображения гиперссылок является выделение

в тексте специальным фоном, цветом или шрифтом ключевых

слов, имеющих определенную смысловую связь с тем фрагмен-

том или документом, на который указывает ссылка. В разви-

тых гипертекстовых системах, как, например, в системе \У\У\У,

в гипертексте могут отображаться также графика (рисунки,

диаграммы), звуковые и даже видеоанимационные элементы,

что в совокупности создает мультимедийную технологию ра-

боты с информацией. В этом случае в качестве гиперссылок

могут также выступать и специальные изображения, значки,

иконки, что дает возможность использования для отображения

283

Документальные

(шформацноппые

системы

связей различных графических ассоциаций. В остальном под-

система отображения гипертекста напоминает обычный тексто-

вый редактор, допуская стандартные операции просмотра

(скроллинг, масштаб) и обработки текста (копирование, кон-

текстный поиск и т. д.).

Подсистема навигации по связям реализует специальный

интерфейс перехода по гиперссылкам. Если гиперссылка ука-

зывает на другой фрагмент того же документа, то подсистема

навигации обеспечивает скроллинг (прокрутку) отображения

текста к соответствующему фрагменту. Если гиперссылка ука-

зывает на внешний документ, то стандартным приемом для си-

стем, реализованных в оконно-графических операционных сре-

дах (М8

\Уш(1о\У8),

является открытие в новом окне соответ-

ствующего документа. Приемом инициализации перехода по

гиперссылке обычно является «щелчок мышью» по ключево-

му слову или графическому значку, обозначающему соответ-

ствующую гиперссылку, либо перевод текстового курсора на

соответствующую гиперссылку и нажатие клавиши

«Еп1ег».

Для осуществления навигации в гипертекстовом докумен-

те для

каэхдой

гиперссылки хранится адрес расположения со-

ответствующего документа или фрагмента. В современных ги-

пертекстовых средах для удобства ориентирования пользова-

теля применяется специальный прием «подсказки» адреса

гиперссылки при осуществлении подготовительных операций

перед ее активизацией (т. е. при переводе курсора мыши или

текстового курсора на гиперссылку непосредственно перед щел-

чком или нажатием клавиши

«Еп1ег»).

Навигация по гиперссылкам формирует для пользователя

определенный

сюжетпо-темапшческий

поток по

цепочке

ас-

социаций. Нетривиальной проблемой,

как

и при навигации в

банках фактографических систем с сетевой моделью организа-

ции данных, является способ отображения и визуализации це-

почек «пройденных» документов. Так как такие цепочки доку-

ментов могут быть неопределенно длинными, то открытие и

отображение каждого следующего по проходу

документа

в до-

полнительном окне приводят к быстрому заполнению, а потом

284

6.4.

Гипертекстовые

ипформацпоппо-попсковые

систем ы

и наслоению окон с документами на экране компьютера. При

этом документ, на который указывает гиперссылка из другого

документа, может помимо непосредственной ассоциации вклю-

чать и совершенно иной содерэ/сательиый контекст, что бьют-

ро «уводит» пользователя от основной темы и дезориентирует

его. Поэтому в большинстве систем используется только одно

окно для отображения документов, а при переходе по гипер-

ссылке к связанному документу происходит «выталкивание»

предыдущего документа в специальный неотображаемый стек

для пройденных документов. Дополнительно обеспечивается

свободная навигация по сформированной таким образом цепоч-

ке документов (по пройденному пути) по принципу

«Вперед-

Назад», что позволяет пользователю путем возвращений назад

или перемещений вперед лучше анализировать сюжетно-тема-

тический поток ассоциаций.

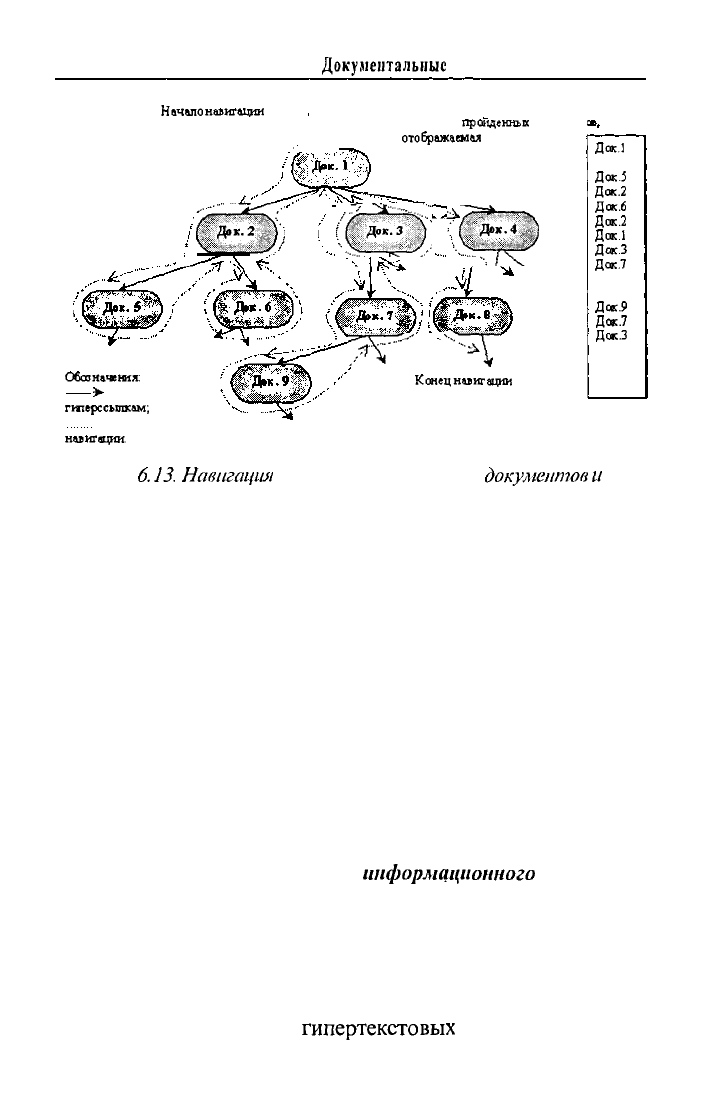
Способ формирования

отобраэ/сепия

цепочки пройден-

ных документов по линейному принципу «Вперед-Назад» не

всегда адекватно позволяет представить схему сюжетно-тема-

тического потока документов из-за наличия возможных ветв-

лений в таких цепочках. Если из какого-либо документа (узла

цепочки) имеется несколько гиперссылок на различные доку-

менты, то сценарием «разговора» пользователя с гипертексто-

вой базой может быть «спуск» от такого документа по имею-

щимся ветвям на определенную глубину, с последующим возвра-

том (подъемом) и спуском по другим ветвям. Л

инейноч:писочный

способ отображения цепочек пройденных документов в этом слу-

чае из-за многочисленных возвратов не дает общего представ-

ления и взгляда на ассоциативную окрестность связанных до-

кументов (см. рис.

6.13).

При наличии только иерархических связей между пройден-

ными документами отработанным приемом отображения

структуры ассоциативной цепочки пройденных документов

может быть способ отображения файловой структуры инфор-

мационных ресурсов компьютера, используемый в программах

типа «Проводник»

операционной

системы

М8

\У1ПС1О\У8

95.

285

Документальные

информационные снстемы

Нач&ло

навигации

.11

Цепочка (линейка)

пройденных

документ

отображ^еми по принципу

"Вперед-Назад":

С^,-

--С^'

Ж"

'Ч

Кспецниигщн к

Д01С.1

Док.2

Док-З

Дм:.2

Ц<ж.6

Дсж.2

Дсж.1

ДосЗ

Док-7

Док.9

Док.7

Док.?

Дж.7

Дм:.3

Док.1

Док.4

Док.г

Обсоначення:

связи по

гтерссьшкам;

> путь

ниигации.

Рис.

6.13.

Навигацш!

по гипертекстовой базе

докумептов

ото-

бражение цепочек пройденных документов

Однако гипертекстовые сети документов, как будет рассмот-

рено ниже, являются не иерархическими, а гетерогенными. В

гетерогенных сетях могут существовать как одноуровневые и

межуровневые связи, так и обратные связи (отсылки), что вы-

рождает само понятие иерархии в таких сетях. Наглядно такие

структуры можно представить в виде неограниченной совокуп-

ности объемно переплетенной паутины узлов, хотя в отдель-

ных сегментах таких структур могут в определенной степени

сохраняться иерархические отношения. Отсюда, видимо, и ро-

дилось соответствующее название для распределенной гипер-

текстовой среды сети Интернет. «Блуждание» по подобным «ла-

биринтам» может образовывать столь запутанные «следы», что

их визуально-наглядное отображение весьма затруднительно.

Вместе с тем визуализация ииформационного поиска до-

кументов является чрезвычайно актуальной задачей, так как

может предоставлять пользователям дополнительные аспекты

анализа информации при аналитических исследованиях. Оп-

ределенные методологические подходы к решению таких за-

дач могут быть найдены на основе анализа семантической при-

роды гетерогенных сетей гипертекстовых документов.

286

6.4.

Гипертекстовые

информационно-поисковые системы

6.4.3. Модель организации данных

в гипертекстовых ИПС

К сожалению, несмотря на интенсивное развитие и всеоб-

щее распространение в последнее десятилетие гипертекстовых

технологий, к настоящему времени еще не проработана полно-

стью формализованная модель организации гипертекстовых

данных, которая бы обеспечивала формализованные процеду-

ры синтеза (разработки, проектирования) и анализа (использо-

вания) гипертекстовых ИПС. Причина этого заключается, как

и в целом для всех типов документальных систем, в пока не-

преодолимых сложностях в формализованном описании смыс-

ла текстов на естественном языке.

Тем не менее в научной литературе имеется ряд работ, по-

священных формальным моделям гипертекстовых

структур^*".

Среди них можно выделить теорию паттернов, разработан-

ную американским математиком У. Гренандером и развитую

впоследствии для гипертекста Л. В. Шуткиным, тензорную

модель А.В. Нестерова и подход логико-смыслового моделиро-

вания, представленный в работах М. М. Субботина, а также ряд

других подходов.

Первые два подхода основываются на формализации от-

дельных текстов специальными математическими конструкци-

ями. В теории паттернов текст рассматривается как сложноор-

ганизованная совокупность отдельных тем, каждая из которых

может выражаться фрагментом текста с минимальным разме-

ром в виде одной строки. Для описания гипертекста в теории

паттернов вводятся также специальные объекты — кнопки

(аналог гиперссылки) и связи с идентификаторами и дополни-

тельными параметрами (тип, направленность и т. д.). В резуль-

тате размеченный гипертекст можно описывать теми или ины-

ми паттерновыми конфигурациями. Вместе

тем теория пат-

тернов не содержит средств синтеза обычного текста в

гипертекст.

"•

См., например, Купер И. Р. Обзор отечественных гипертекстовых технологий

//Теория и практика общественно-научной

информации.

— Вып.

13.

—1997.

287

Документальные

информационные системы

Тензорный подход основывается на идеологии ранее рас-

сматривающейся фасетной классификации, которая позволяет

формализовано описать смысловую структуру текста в

виде

тензора-',

а гипертекстовую структуру в виде ансамбля тензо-

ров. Таким образом, сильной стороной тензорного подхода яв-

ляется возможность создания формализованных процедур ана-

лиза исходных текстов для создания гипертекстовых структур.

Наиболее развитым в практическом плане является подход,

основанный

\\а

логико-смысловом моделировании человечес-

кого мышления, позволяющий на основе семантической бли-

зости текстовых фрагментов связывать их в цельный осмыс-

ленный

текст

—

семантическую сеть. Математическим аппа-

ратом для описания структуры гипертекста выступает теория

графов. Критерием для связывания текстов или их фрагментов

в семантическую сеть является возможность установления меж-

ду ними логических связок типа «есть», «является условием»,

«является причиной» и т. д. Построение на основе анализа тек-

ста таких связываний образует формализованные «высказыва-

ния», комбинируя которые можно получать определенные вы-

воды или, как говорят, новые знания, или подтверждать истин-

ность (доказывать) составных высказываний. В наиболее

развитом виде такой подход реализуется в так называемых ба-

зах знаний, составляющих основу особой ветви информацион-

ных систем, называемых экспертными системами.

Таким образом, при логико-смысловом моделировании

структура гипертекста представляет (точнее, должна представ-

лять) систему семантических связей между когнитивными эле-

ментами (понятиями, высказываниями) определенной предмет-

ной области. В результате сильной стороной такого подхода

является возможность автоматизации создания (разметки) ги-

пертекстовых структур на основе распознавания и соотнесения

упрошенном виде тензор можно трактовать как математический объект, за-

вершающий иерархически усложняющуюся

цепочку

—

«скаляр

—

вектор—тензор»,

т. е. как многокомпонентный объект в многомерном пространстве с заданным линей-

ным

преобразоваипе\г

его компонент при переходе от одной системы координат к дру-

гой.

288

6.4.

Гипертекстовые

ипфоршацпоппо-поисковые

системы

документов или их фрагментов к тем или иным узлам семанти-

ческой сети.

Если вернуться к структуре гипертекстовой ИПС (рис. 6.12),

то ее центральным элементом является гипертекстовая база

документов. По принципу формирования и управления гипер-

текстовыми базами их можно разделить на открытые (физи-

чески распределенные, или децентрализованные) и замкнутые

(локально сосредоточенные).

В замкнутых базах гипертекстовые документы находятся

в едином локалыю-сосредоточеппом и централизованно управ-

ляемом хранилище (файле или группе файлов со специальным

форматом). Такое хранилище образует

зал/кпутум

семанти-

ческую сеть документов, гипертекстовые связи которых не вы-

ходят за пределы хранилища. Соответственно

внесение

в базу

новых документов или удаление документов производится не-

посредственно в месте расположения такой локальной базы.

В открытых базах гипертекстовые документы не образу-

ют единое локально

рсвмещенное

хранилище, а располагаются

автономно в любых элементах (узлах) информационной сре-

ды. При этом информационная среда может ограничиваться

файловой структурой одного компьютера (диски, каталоги, под-

каталоги),

локсшьной

или глобальной информационной сетью.

В открытых базах семантическая гипертекстовая сеть докумен-

тов не управляется из одного центра (узла), а совместно стро-

ится и поддерживается всеми пользователями, работающими в

узлах информационной среды (сети). Несмотря на полную де-

централизацию создания и функционирования, при определен-

ных соглашениях (протоколах) об установлении и поддержа-

нии связей-гиперссылок, такие открытые семантические струк-

туры тем не менее представляют единый развивающийся по

определенным закономерностям организм.

В настоящее время техника гиперссылок, применяемая в

гипертекстовых системах, предполагает лишь однонаправлен-

ные связи, позволяющие осуществлять навигацию только в

прямом направлении. «Вернуться» обратно в исходный доку-

мент можно только по запомненной цепочке пройденных доку-

289

6. Документальные информационные системы

ментов, т. е. по схеме «Вперед-Назад». При этом прямой пере-

ход по гиперссылке осуществляется из определенного места,

точнее контекста исходного документа, а возврат осуществля-

ется обратно в документ в целом, т. е. фактически в его начало,

что может разрывать контекст (сюжетно-тематический поток)

анализа информации. В ранних гипертекстовых системах (про-

ект Хапа(1и) предполагался двунаправленный характер гипер-

ссылок, но практическая реализация такого подхода существен-

но усложняет протоколы навигации, так как требует более де-

тального координатного адресования объектов и субъектов

гиперссылок, идентифицирования пользователей и поддержа-

ния устойчивости документов (в смысле координатной струк-

туры).

В результате модель организации данных в гипертексто-

вых базах описывается ориентированными

невзвешенпылш

гра-

фсши

с петлями и циклами. По определению граф (7 представ-

ляет структуру, состоящую из множества вершин

х^, х^..

.,х^^ и

множества ребер а^, а^..

.,а„^

их соединяющих. По ребрам осу-

ществляется движение, переход от одной вершины к другой.

Ориентированные ребра, по которым переход возможен только

в одном направлении, называются дугами. Применительно к

структуре гипертекстовой базы вершины графа соответствуют

документам, а дуги гиперссылкам. Невзвешенность означает

равнозначность любых

дуг

по переходу, или, иначе говоря, оди-

наковую «стоимость» перехода по любой гиперссылке. Петлей

называется дуга, начальная и конечная вершины которой со-

впадают, т. е. применительно к гипертексту внутренняя гипер-

ссылка на другой фрагмент того же документа. Путем (или ори-

ентированным маршрутом)

нгизывается

последовательность дуг,

в которой конечная вершина любой дуги, кроме последней, яв-

ляется начальной вершиной следующей дуги. В невзвешенном

графе, когда стоимость (вес) всех дуг одинакова, длиной пути

является число дуг, входящих в путь. Путь

а^, а^...,

называ-

ется замкнутым, если в нем начальная вершина первой дуги

а^

совпадает с конечной вершиной последней дуги

. Если в зам-

кнутом пути любая вершина графа используется не более од-

290