Галуев Г.А. Математические основы криптологии

Подождите немного. Документ загружается.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ

ФЕДЕРАЦИИ

ТАГАНРОГСКИЙ ГОСУДАРСТВЕННЫЙ

РАДИОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Галуев Г.А.

МАТЕМАТИЧЕСКИЕ ОСНОВЫ

КРИПТОЛОГИИ

Учебно-методическое пособие

Таганрог 2003

Кафедра безопасности информационных технологий

УДК 681.3.067(075.8)

Галуев Г.А. Математические основы криптологии:

Учебно-методическое пособие. Таганрог: Изд-во ТРТУ

2003.-120с.

В настоящем пособии изложены математические элементы

теории чисел и теории поля, лежащие в основе построения со-

временных криптографических систем, а также вопросы синтеза

и анализа криптоалгоритмов.

Пособие предназначено для изучения лекционного курса

"Математические

основы криптологии" студентами специально-

стей 075400, 075300, 075600.

Табл. 4. Ил. 7. Библиогр.: 7 назв.

Рецензент И. А. Каляев,

д.т.н., профессор, директор НИИ МВС

СОДЕРЖАНИЕ

1. Основные понятия криптографии. История развития

криптографии, примеры классических криптосистем.

Современные криптосистемы. Схемы атаки на шифр

(группы методов дешифрования). 4

2. Стойкость криптографических систем и алгоритмов.

Информационно - теоретический подход и подход на

основе теории сложности. 15

3. Элементы теории чисел: основные понятия и теоремы. 24

4. Элементы конечного поля. Основные понятия и

свойства алгебраических структур. 38

5. Элементы теории конечного поля. Основные понятия

и теоремы. 48

6. Элементы теории конечного поля. Строение конечных полей.

Основные свойства и методы построения конечных полей. 56

7. Элементы теории конечного поля. Многочлены над

конечными полями. 64

8. Элементы теории конечного поля. Линейные

рекуррентныепоследовательности над конечными полями. 74

9. Дополнительные математические элементы криптографии. 82

10. Общая характеристика различных типов шифров и

классов криптосистем. 90

11. Методы формирования псевдослучайных

последовательностей. Схема открытого распределения

ключей Диффи и Хеллмана. 99

12. Алгоритм RSA и алгоритм Эль Гамаля работы

криптосистем с открытым ключом. Цифровая подпись.

Алгоритм цифровой подписи Эль Гамаля. 106

Список рекомендуемой литературы. 117

1. Основные понятия криптографии. История

развития криптографии, примеры классических

криптосистем. Современные криптосистемы.

Схемы атаки на шифр (группы методов

дешифрования).

Криптология – наука о создании и анализе систем безо-

пасности связи. Говоря о криптологии, иногда имеют в виду не

безопасную, а секретную связь. Однако секретность является

только одним элементом безопасности или целостности инфор-

мации. Целостность информации связана с вопросами подлин-

ности, своевременности, согласованности и т.д., а также со все-

ми вопросами, обычно возникающими с документными запися-

ми.

Криптологию принято делить на две части: криптографию

и криптоанализ. Криптография - это наука о методах обеспече-

ния секретности и подлинности (идентичности) данных при их

передаче по линиям связи или хранении. Криптоанализ – это

наука о методах раскрытия или подделки данных. Иными слова-

ми криптография и криптоанализ нацелены на решение взаимно

обратных задач.

Цели криптографии менялись на протяжении всей её исто-

рии. Сначала она служила только для обеспечения секретности,

чтобы препятствовать несанкционированному доступу к инфор-

мации, передаваемой по военным и дипломатическим каналам

связи. По мере развития информатики криптография носила ши-

рокое применение для защиты информации во многих приклад-

ных областях: истории болезни, юридические и финансовые до-

кументы, закрытые коммерческие данные и т.п. В настоящие

время криптография используется не только не только для защи-

ты информации от несанкционированного доступа, но и для

обеспечения её подлинности и целостности криптографических

систем применяются физическая защита, различные организаци-

онно - технические мероприятия и стеганография. Стеганогра-

фия занимается методами скрытия самого факта передачи со-

общения (симпатические чернила, молоко для написания текста,

шумоподобные методы радиопередачи и д.р.).

Наиболее эффективная защита информации обеспечивает-

ся сочетанием всех этих способов.

Открытым текстом называют исходные сообщение, ко-

торое должен защищать криптограф.

Шифр - это множество обратимых преобразований формы

открытого текста, проводимых с целью его защиты.

Процесс применения обратимого преобразования

шифра к

открытому тексту называется зашифрованием, а результат этого

преобразования - шифротекстом или криптограммой. Соот-

ветственно процесс обратного преобразования шифротескта в

открытый текст называется расшифрованием. Совокупность

данных, определяющих конкретное преобразование из множест-

ва преобразований шифра, называют ключом. Такой ключ, в ча-

стности, может передаваться отправителем получателю заранее

до отправления криптограммы каким - либо надежно защищен-

ным способом. Дешифрование - атака на шифр, раскрытие

шифра со стороны взломщика. Специальным видом шифра яв-

ляется код. Код - это своего рода словарь, где элементы откры-

того текста (буквы, сочетания букв, слова и даже фразы) так на-

зываемые кодвеличины заменяются группами символов (букв,

цифр, других знаков). Эти группы символов называют кодообо-

значениями. Принципиальной разницы между шифром и кодом

нет.

Одним из основных понятий криптографии является стой-

кость. Стойкость - это способность противостоять попыткам

хорошо вооруженного современной техникой и знаниями крип-

тоаналитика дешифровать перехваченный шифротекст, раскрыть

ключи шифра или нарушить целостность и подлинность инфор-

мации.

В истории развития криптографии можно условно выде-

лить три основных этапа. Первый период - эра донаучной крип-

тологии, являющейся уделом узкого круга искусных умельцев.

Началом второго периода можно считать 1949 год, когда появи-

лась работа известного американского ученого Клода Шеннона

«Теория связи в секретных системах». В этой работе проведено

фундаментальное научное исследование шифров и вопросов их

стойкости, благодаря чему криптология оформилась как при-

кладная математическая наука. Третий период связывают с по-

явлением в 1976 году работы У. Диффи и М. Хеллмана «Новые

направления в криптографии, « где показано, что секретная

связь возможна без предварительной передачи секретного клю-

ча.

Ещё несколько веков назад само применение письменности

можно было рассматривать как способ закрытия информации,

т.к. владение письменностью было уделом немногих.

Один из самых древних шифротекстов, написанных клино-

писью, был обнаружен в Месопотамии и датируется XX веком

до н.э. Известны также древнеегипетские религиозные и меди-

цинские шифротексты.

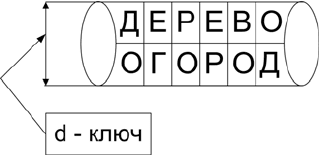
В середине IX века до н.э. использовалось шифрующие

устройство - скиталь для получения шифра перестановки. При

шифровании слова писались на узкую ленту, намотанную на ци-

линдр, вдоль образующей этого цилиндра (скиталя). После этого

лента разматывалась и на ней оставались переставленные буквы

исходного текста. Ключом в этом случае являлся диаметр этого

цилиндра.

В начале нашей эры создается шифр замены. Так в 56 году

н.э. во время войны с галлами Юлий Цезарь использует шифр

простой замены, строящийся следующим образом:

Под алфавитом открытого текста пишется тот же алфавит

со сдвигом на три позиции по циклу. При шифровании буквы

открытого текста у верхнего алфавита заменялись буквами ниж-

него алфавита.

А Б В Г Д Е Ж … Э Ю Я

Г Д Е Ж … Э Ю Я А Б В

Более сложной разновидностью шифра замены является

«квадрат Полибия».

1 2 3 4 5

1 A B C D E

2 F G H J K

3 L M N O P

Q R S T U

V W X Y Z

При шифровании буквы открытого текста заменяются па-

рой чисел: номер столбца и номер строки соответствующей бук-

вы в таблице

Открытый текст:

R E A D Y

Шифротекст: 24 51 11 41 45

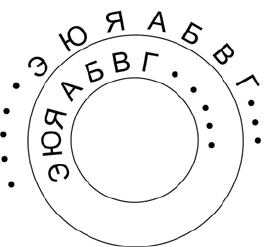
В начале

XV века н.э. Альберти предложил оригинальный

шифр замены, на основе двух концентрических кругов, по ок-

ружности которых записывались алфавиты открытого текста и

шифротекста. При этом шифроалфавит был не последователь-

ным АБВГ… ЭЮЯ, а произвольным АЭВЮГ… и мог быть еще

и смещен на любое число позиций.

Здесь была впервые реализована идея увеличения стойко-

сти шифросистемы путем повторения шифрования с помощью

разных шифросистем (меняя последовательность шифроалфави-

та и его сдвиг относительно алфавита открытого текста).

В XVI веке н.э. французский дипломат Вижинер предло-

жил оригинальный шифр сложной замены, получивший впо-

следствии название системы Виженера

Система Виженера.

Шифруемый текст ЗАЩИТАИНФОРМАЦИИ

Ключ МОРЕМОРЕМОРЕМОРЕ

Зашифрованный текст УОИОЭОШТЯЫЯСМГШО

АБВГДЕЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ

↓

М МНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЖЗИКЛ

О ОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЖЗИКЛМН

Е СТУФХЦЧШЩЪЫЬЭЮЯАБВГДЕЖЗИКЛМНОП

Р ЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯАБВГД

АЛГОРИТМ ШИФРОВАНИЯ:

1. Под каждой буквой открытого текста записываются бук-

вы ключи, повторяющие ключ требуемое число раз (чтобы по-

крыть все буквы текста).

2. Шифруемый текст по подматрице МОРЕ заменяется бу-

квами, расположенными на пересечении линий, соединяющих

буквы первой строки и буквы ключа, находящейся под ней.

Алгоритм расшифрования

Ключ МОРЕ МОРЕ МОРЕ МОРЕ

Шифр УОИО ЭОШТ ЯЫЯС МГШО

Расшифрованный текст ЗАЩИ ТАИН ФОРМ АЦИИ

В строках М,О,Р,Е отыскиваются буквы шифрованного

текста и заменяются буквами первой строки. Это шифр слож-

ной замены или многоалфавитный шифр замены.

В тоже время Ф. Бекон впервые предложил представление

букв алфавита пятизначным двоичным кодом: А - 00001, Б -

00010… Такой способ шифрования обладал слабой стойкостью,

однако эта идея, через три столетия легла в основу электриче-

ской и электронной связи на основе кодов Морзе, Бодо, теле-

графных кодов.

Известный математик К. Гаусс в 18 - 19 веках создал шифр

с многократной подстановкой или равночастный шифр в ос-

нове которого лежит прием рандомизации (random - случай-

ный) открытого текста, который преобразовался в шифротекст,

содержащий символы большего алфавита. При этом часто

встречающиеся буквы открытого текста заменяются случайными

символами из большего алфавита. В результате все символы

шифротекста равночастны.

В нашем столетии американский ученый Вернам предло-

жил систему побитового шифрования открытого текста, пред-

ставленного телеграфным двоичным кодом, когда каждый бит

преобразуется с использованием бита ключа по алгоритму

000 011 101 110⊕= ⊕= ⊕= ⊕=

Сложение по модулю два.

Вернам предполагал использовать ключ только один раз.

Длина ключа равна длине шифруемого открытого текста. Впо-

следствии К. Шеннон доказал что такой шифр не раскрываем.

Однако сложности формирования, хранения и передачи ключа,

длина которого равна длине открытого текста делают такой ме-

тод очень непрактичным и дорогостоящим

В целом при построении шифров могут использоваться

ключи разных типов: долговременные, суточные и сеансовые

(для передачи каждого конкретного сообщения).

В настоящие время вместо понятия шифра используется

понятие криптографической системы с секретным ключом, ко-

торая задается следующими пятью компонентами:

- пространство открытых текстов

- пространство шифрованных текстов

- пространство ключей

E - (

∈

) множество преобразований зашифрования

)( :

~~~

KkCME

∈→

D (

∈ ) - множество преобразований расшифрова-

ния

)( :

~~~

KkMCD

∈→

Преобразования

E и

D для всех (

∈

) и любого от-

крытого текста

∈

должны удовлетворять условию

mmED

)]([

Согласно основному правилу Керкхофа множества

E и

D могут быть известны не только криптографу, но и криптоа-

налитику. Секретность же сообщения обеспечивается сокрытием

того факта, какое именно преобразование из известного множе-

ства используется для зашифрования.

Современные криптосистемы с секретным ключом подраз-

деляются на блочные и потоковые.

Блочная криптосистема разбивает открытый текст

на

блоки ...,

MM и зашифровывает каждый блок с помощью од-

ного и того - же обратимого преобразования

E , выбранного в

соответствии с ключом К

)...(),()(

MEMEME

kkk

Для повышения стойкости блочных криптосистем исполь-

зуется режим сцепления блоков шифра (СВС). Если обозна-

чить через

E преобразование зашифрования в режиме сцепле-

ния блоков

,...,

шифрованного текста из блоков

...,

MM открытого текста, то процесс этого зашифрования в

режиме сцепления блоков шифра описывается соотношением

,...2,1] [

⊕

−

iMCEC

iiki

Начальные значение

C является несекретным и передает-

ся вместе с шифротекстом.

Соответственно процесс расшифрования

D описывается

соотношением

,...2,1 ][

⊕

−

iCCDM

iiki

Иногда используют более сложные режимы сцепления

блоков шифра

,...2,1

)(

⎩

⎨

⎧

⊕⊕=

−−

CDMCM

MCMEC

PCP

ikiii

iiiki

,...2,1

)(

⎩

⎨

⎧

⊕=

−

CDMM

MMEC

PCB

ikii

iiki

Поточная криптосистема разбивает открытый текст М на

буквы или биты m1,m2,… и зашифровывает каждый знак

m с

помощью обратимого преобразования

E , выбранного в соот-

ветствии со знаком

k ключевого потока ,...,

kk .

Такие системы иногда называют системами гаммирова-

ния, а последовательность ,...,

kk называют гаммой.

Примерами поточной криптосистемы является система

Вернама (о которой говорилось выше), где

1,0, ,..., 2,1 )(. .

,...)(, )(

222111

∈=⊕=

⊕

iiiiik

kmikmmEет

kmmEkmmE

В свою очередь поточные криптосистемы делятся на син-

хронные и самосинхронизирующиеся.

Синхронные поточные криптосистемы характеризуются

тем, что, в отличие от самосинхронизирующихся, в них ключе-

вой поток ,...,

kk получается независимо от открытого и

шифрованного текстов.

Самосинхронизирующиеся поточные криптосистемы

характеризуется тем, что каждый знак ключевого потока (гам-

мы) в любой момент времени определяется фиксированным чис-

лом предшествующих знаков шифротекста.

Алгоритм, который вырабатывает ключевой поток (гамму)

может быть либо детерминированным, либо случайным, Этот

алгоритм называют генератором ключевого потока. Если та-

кой генератор детерминированный, то он должен зависеть от

секретного ключа. Если он случайный то сам является секрет-

ным ключом, но очень большой длины, что непрактично.

Описать работу генератора ключевого потока можно на

языке теории автоматов, используя понятия функции переходов

F и функции выходов f. Тогда работу синхронной поточной

криптосистемы описать соотношениями

(, )

(, ).

SFkS

kfkS

⎧

⎨

⎩

Начальные значения

S (начальное состояние автома-

та) может быть функцией от ключа k.

Соответственно работа самосинхронизирующейся поточ-

ной криптосистемы описывается соотношением

⎩

⎨

⎧

−−−

),(

],...,,[

niiii

Skfk

CCCFS

Сложность построения поточных криптосистем связана с

необходимостью построения хороших генераторов ключей, что-

бы, например, нельзя было бы по известному отрезку открытого

и шифрованного текстов восстановить всю ключевую последо-

вательность.

Одним из эффективных подходов и построению генерато-

ров ключей является счетчиковым метод, предположенный

Диффи и Хеллманом.

В общем случае работа генератора ключей описывается

соотношением

()

(, ).

SFS

kfkS

⎧

⎨

⎩

Функция перехода F не зависит от ключа, но преобразова-

ние F выбирается так что генерирует перебор всех или почти

всех возможных состояний генератора при изменении времени

i=1,2,…

В качестве F используется преобразование регистров сдви-

га с линейной обратной связью, вырабатывающие последова-

тельности максимального периода, или просто счетчики (со-

стояния которых меняются пребыванием единицы) с заданным

коэффициентом пересчета (счетчики о заданному модулю). В

качестве функции выхода f используется преобразование за-

шифрования

E блочного шифра.

В последнее время широкое распространение получили

криптосистемы с открытым ключом, построенные на основе

предложенных Диффи и Хеллманом принципов открытого шиф-

рования и открытого распределения ключей (1976 г.). Также

криптосистемы называют также двух ключевыми криптоси-

стемами или асимметричными криптосистемами, в то время

как обычные криптосистемы с секретным ключом называют

симметричными криптосистемами. Принципы построения

таких криптосистем и лежащих в их основе криптоалгоритмов

рассмотрим на последующих лекциях

Современный уровень развития электронной и информа-

ционной технологий позволяет криптоаналитику относительно

легко получить доступ к передаваемым по линиям и системам

связи сообщениям, как обычного типа, так и секретным в виде

криптограмм или шифротекстов. В связи с этим, основной зада-

чей криптоаналитиков является атака на криптограмму при не-

известном ключе с целью раскрытия (дешифрования) шифра. В

целом, в зависимости от уровня доступной криптоаналитику

информации, можно выделить четыре возможные схемы атаки

на шифр или четыре типа методов дешифрования:

1. Схема атаки на шифр (методы расшифрования) на осно-

ве знания только шифротекста

C →

2. Схема атаки на шифр (методы дешифрования) при из-

вестных открытом M и шифрованном C текстах.

→,

Такая ситуация возможна когда приходится шифровать

общеизвестные данные, например, дипломатические документы,

секретные только до момента их опубликования, или когда с

достаточной степенью вероятности можно предполагать наличие

в тексте тех или иных слов и выражений.

3. Схема атаки на шифр (методы дешифрования) по выби-

раемому открытому тексту и соответствующему ему шифрован-

ному тексту, т.е. атака на основе тестирования. Выбираемые

Сующиесоответств

→→

Такая ситуация возможна когда криптоаналитик имеет

доступ к шифровальному аппарату или шифрующему преобра-

зованию

и может получить для любого выбранного открыто-

го текста соответствующий ему шифротекст.

4.Схема атаки на шифр (методы дешифрования для крип-

тосистем с открытым ключом) по выбранным шифротекстам и

соответствующим открытым текстам Выбираемые

Сующиесоответств

→→

Такая ситуация возможна, когда криптоаналитик имеет

доступ к преобразованию расшифрования

D и может получать

для выбранных шифротекстов С соответственно открытые тек-

сты М.

2. Стойкость криптографических систем и

алгоритмов. Информационно - теоретический

подход и подход на основе теории сложности.

Основным назначением криптосистем является обеспече-

ние передачи секретных сообщений через несекретные каналы

связи. Поэтому важнейшей характеристикой любой криптоси-

стемы является ее стойкость, т.е. способность противостоять

попыткам дешифровать перехваченный шифротекст или рас-

крыть ключи шифра.

Исторически первым подходом к определению стойкости

криптосистем был информационно - теоретический подход,

предложенный К. Шенноном. Этот подход основан на понятии

информации, ее количественной оценке и анализе количества

информации об открытом тексте, для обеспечения стойкости

криптосистемы.

Формально количество информации в сообщении измеря-

ется энтропией.

Пусть

xx ,...,

есть n возможных сообщений, появляю-

щихся с вероятностями

∑

xPпричемxPxP

1)( ) (),...,(

Тогда энтропия сообщения x есть

() ( )log ( ) ( )log

()

ii i

Hx Px Px Px

=− =

∑∑

Для заданного n величина H(x) принимает max значение,

равное

log

при

xPxP

)(...)(

===

т.е. когда все сообщения равновероятны. Неопределен-

ность (энтропия) уменьшается, когда распределение вероятно-

стей сообщений становится все более отличным от равновероят-

ного и достигает min H(X)=0 когда 1)(

xP для некоторого

сообщения

x . Энтропия сообщения измеряет его неопреде-

ленность в числе бит информации, которая должна быть восста-

новлена, когда сообщение было скрыто от криптоаналитика в

шифротексте.

К. Шеннон различал теоретическую и практическую стой-

кость криптосистем. Криптосистема называется теоретически

стойкой, если криптоаналитик не может уточнять распределе-

ние вероятностей возможных открытых текстов по имеющемуся

и у него шифротексту, даже если он обладает всеми необходи-

мыми для этого средствами. При этом предполагается, что сек-

ретный ключ используется только один раз (т.е. сеансовый ре-

жим использование ключа).

Совершенная секретность означает, что открытый текст

М и шифротекст С статистически независимы т.е. совпадают ве-

роятности

)()/(

для всех возможных M и C и получение шифротекста не

дает криптоаналитику дополнительной информации о послан-

ном открытом тексте.

Определение совершенной секретности можно также пред-

ставить в виде

)()/(

Пусть P(C/M) - условная вероятность получения шифро-

текста С при условии, что известно, что зашифрован текст М на

некотором неизвестном ключе. Тогда

:()

(/ ) (),

kE M C

PC M Pk

∑

где

- вероятность использования ключа

- пре-

образование зашифрования на ключе

Обычно существует по крайней мере один ключ

, такой

что CME

)( для данных М и С, но иногда текст М может

быть зашифрован в текст С при нескольких различных ключах.

Необходимым и достаточным условием для совершенной

секретности является то, что для каждого С и для всех М выпол-

нено

)()

( C

= ,

т.е. вероятности получения конкретного шифра С, при условии

что был зашифрован текст М, одинаковы для всех М.

Используя то факт, что уменьшение объема известных све-

дений может лишь увеличить неопределенность, т.е. энтропию,

получим

(/) (,/) (/) (/,)

(/) ()

HM C HMK C HK C HM CK

HK C HK

≤

=+ =

=≤

(Здесь естественно

0),

(

, т.к. ключ секрет-

ный). Другими словами неопределенность секретного ключа

должна быть не меньше, т.е.

≥ неопределенности шифруемого с

его помощью текста отсюда можно сделать вывод, что размер

ключа

не должен быть меньше размерности открытого текста

М. Такое условие является очень жестким, т.е. это практически

очень неудобно (слишком большие по размеру секретные ключи

равные длинам передаваемых сообщений). Примером совер-

шенно секретной криптосистемы является рассмотренная на

прошлой лекции система Вернама когда

{}

KMKMKMC

⊕

⊕=

⊕

,...,

при случайном равновероятном выборе ключа

kkk ,...,

= и

−

= 2)(

для всех i=1,…,n, откуда

MCP

−

= 2)/(

для всех С и М т.е. выполняется условие совер-

шенно секретной системы.

Помимо теоретической стойкости криптосистемы рассмат-

ривают ее

практическую стойкость. Для этого вводят рабочую

характеристику

W(n) - среднее количество работы (измеренное

в удобных единицах), требуемое для нахождения ключа

на

основе знания

n знаков шифротекста с помощью наилучшего

криптоаналитического алгоритма. Обычно криптосистемы оце-

нивают с помощью достигнутой оценки рабочей характеристики

W( ∞ ) при использовании наилучшего из известных методов

дешифрования. Криптосистемы называются

практически

стойкими

если они не могут быть вскрыты в течение реального

времени (

Cons

W ≥∞)( ) всеми общедоступными методами.

На практике используют именно это понятие стойкости крипто-

систем. По сути дела из этого определения можно сделать вывод

о том, что проблема создания практически стойких криптоси-

стем или шифров может быть сведена к проблеме нахождения

наиболее сложных задач, удовлетворяющих определенным ус-

ловием. Можно составить шифр таким

образом, чтобы раскры-

тие его было эквивалентно (или включало в себя, решение неко-

торой задачи, про которую известно, что для ее решения требу-

ется определенный (желательно большой объем) работы). По-

этому стойкость криптосистемы можно определить вычисли-

тельной сложностью алгоритмов, применяемых криптоаналити-

ками для шифрования. Такой подход к определению стойкости

криптосистем, основанный

на понятии вычислительной сложно-

сти криптоаналитических алгоритмов (в отличие от информаци-

онно - теоретического, рассмотренного выше) основан не на во-

просе о том возможно ли извлечь информацию об открытом тек-

сте из анализа шифротекста, а на вопросе о том, осуществимо ли

это в приемлемое время. Этот подход позволяет достичь свойст-

ва

совершенной секретности криптосистемы даже для случаев,

когда используется секретные ключи значительно меньше по

размерам чем длина открытого шифруемого текста.

Вычислительная сложность алгоритма в свою очередь

измеряется его временной

и емкостной S сложностями в зави-

симости от размера

n входных данных.

Временная сложность - это время, затрачиваемое алго-

ритмом для решения задачи, рассматриваемое как функция раз-

мера задачи или количества входных данных.

Емкостная сложность - это емкость необходимой ма-

шинной памяти. Поведение этих сложностей в пределе при уве-

личении размера задачи называется

асимптотическими слож-

ностями. Эти сложности алгоритма определяют в итоге размер

задачи, которую можно решить этим алгоритмом.

Если при данном размере задачи в качестве меры сложно-

сти берётся наибольшая из сложностей по всем входам этого

размера, то она называется

сложностью в худшем случае. Если

в качестве меры сложности берется «средняя» сложность по

всем входам данного размера, то она называется

средней слож-

ностью. Обычно среднюю сложность найти труднее чем слож-

ность в худшем случае.

Теория сложности в основном имеет дел со сложностью

задач в худшем случае. Для анализа работы алгоритма нужны

модели вычислительных машин, достаточно точно отражающих

основные черты реальных машин. В качестве таких моделей ис-

пользуются машины с

произвольным доступом к памяти, ма-

шины с

произвольным доступом к памяти и хранимой про-

граммой, детерминированная и недетерминированная маши-

ны Тьюринга и другие.

Если алгоритм обрабатывает входы размера

n за время

cn ,где с - const, то говорят что временная сложность этого ал-

горитма есть

)(

(читается порядка

n ). Строго в математи-

ческом смысле: неотрицательная

))(( ) (

Oестьn

если

существуют постоянные

с и

n , для которых

( ) | ( ) | .gn c f N ïðèn n

≤

≥

110

( ) ...

ñëè g n a n a n a n a

−

++++

, то

)(n

явля-

ется

полиномиальной функцией степени m т.е.

)( ) (

nOng =

Полиномиальным алгоритмом или алгоритмом поли-

номиальной временной сложности называется алгоритм, у ко-

торого временная сложность равна

))(( n

, где Р(n) - неко-

торый полином, а n - размер задачи (входа). Алгоритмы, вре-

менная сложность которых есть

=0(

)(nP

c ), где с -const, Р(n) -

полином, называется

экспоненциальными.

Для примера в таблице приведены времена для различных

классов алгоритмов при

10=n

на обычной последовательной

ЭВМ с быстродействием

операций в секунду.

Класс

алгоритма

Слож-

ность

Число опера-

ций при

Реальное

время

Полиномиаль-

ный

O(1)

1 1 мс.

Линейный

O(n)

1сек.

Квадратичный

O(n

)

10 дней.

Кубический

O(n

)

27397 лет.

Экспоненци-

альный

O(2

)

30130

301016

лет.

Из таблицы видно, что при

=О(n

)выполнение алгоритма

становится практически невозможно на последовательной ма-

шине. Однако на машине с 10

параллельно работающими про-

цессорами вычисление алгоритма сложностью

=О(n

) может

занять 10 дней. В тоже время вычисление алгоритма сложностью

=О(2

) практически невозможно даже на параллельной машине

с одним триллионом процессоров.

Задачи, которые решаются за полиномиальное время назы-

ваются

решаемыми, так как они обычно могут быть решены для

задач достаточно большой размерности

n. Задачи, которые не

могут быть систематически решаемыми за полиномиальное вре-

мя называют нерешаемыми или просто трудными.

Существуют и

алгоритмически неразрешимые задачи,

для которых невозможно создать алгоритм решения. Например,

десятая проблема Гильберта: существует ли алгоритм, решаю-

щий в целых числах уравнение

0),...,(

xxP

для многочлена

Р с целыми коэффициентами. Доказано,

что такого алгоритма не существует.

На рисунке представлена классификация задач по степени

их сложности и дано их возможное наглядное соотношение друг

с другом (точно это соотношения не известно).