Галуев Г.А. Математические основы криптологии
Подождите немного. Документ загружается.


21
Класс
Р или P - TIME состоит из всех задач, решаемых за
полиномиальное время. Класс
NP или NP - TIME, состоит из
всех задач решаемых за полиномиальное время на недетермини-
рованной машине Тьюринга, способной параллельно выполнять
неограниченное количество независимых вычислений. Это озна-
чает, что если вариант решения проверяется, то он может быть
проверен на такой машине Тьюринга за полиномиальное время.
Конечно, это не означает решить задачу, так как нет гарантии,
что машина проверяет правильно отгаданное решение. Чтобы
проверить все варианты решения и найти нужное (т.е. чтобы
решить задачу из NP класса), по-видимому, необходимо затра-
тить экспоненциальное время. Примером такой задачи является
известная «задача рюкзака»: имеется множество из n целых чи-
сел
A=(a
1
,…,a
n
) и целое число S. Требуется определить, сущест-
вует ли подмножество чисел из
А такое, чтобы их сумма была
бы равна
S. Эта задача принадлежит к классу NP задач, так как
для любого подмножества чисел из
А легко проверить равна ли
их сумма
S. Найти же такое подмножество чисел, сумма кото-
рых равна
S гораздо труднее. Существует 2
n
таких подмножеств
и проверка их всех имеет временную сложность
τ
=О(2
n
).
Класс
NP включает класс P, так как любая задача, полино-
миально решаемая на детерминированной машине Тьюринга,
может быть полиномиально решена и на недетерминированной
22
машине Тьюринга. Еще никто не доказал, что
NP=P также как и
то, что
P
NP
≠
.
Основной метод, используемый для доказательства близо-
сти по сложности задач, состоит в сведении задач друг к другу с
помощью
конструктивного преобразования. Известно много
примеров такого преобразования. В 1971 году Кук доказал тео-
рему, согласно которой любая задача о выполнимости имеет
свойство, что каждая другая задача из
NP класса может быть
сведена к ней за полиномиальное время. В тоже время Карп до-
казал, что многие хорошо известные комбинаторные задачи,
включая задачу «о коммивояжере» (выбрать маршрут, посеще-
ния разных городов так, чтобы в каждый город попасть только
один раз) столь же трудны, как и задача о выполнимости.
Класс
NP Complete (NP - полных) задач включает все са-
мые трудные
NP задачи. Если какая - либо из NP полных задач
окажется в классе
P, то будет доказано равенство NP=P
Класс
С
0
NP состоит из всех задач, являющихся дополни-
тельными для некоторых задач из
NP. Если задача в NP имеет
вид: «определить существует - ли решение», то задача из
CoNP
имеет вид «показать, что решений нет». На сегодняшний день не
известно верно - ли равенство CoNP=NP, но есть задачи, при-
надлежащие пересечению классов
CoNP и NP т.е. CoNP
∩
NP.
Примером такой задачи является «задача о разложении чисел»:
дано целое число n, определить существуют - ли делители p и q,
такие что
n=pq. Эта задача нашла плодотворное применение в
криптологии. При этом, задача нахождения делителей
p и q
сложнее, чем задача установления разложимости числа
n (раз-
ложимость
n можно установить проверкой равенство n=pq при
выбранных
p и q, что достаточно просто сделать)
Класс
PSPACE состоит из задач, требующих полиноми-
альных объемов машинной памяти, но не обязательно решаемых
за полиномиальное время. Этот класс включает классы
CoNP и
NP (CoNP - Complete и NP.Complete), но есть в нем задачи, ко-
торые труднее чем
CoNP(CoNP - complete) и NP(NP - complete).
Класс
PSPACE - complete (полных) задач состоит из задач,
имеющих свойство, что если какая-нибудь из них окажется при-

23
надлежащей классу
NP, то NP=PSPACE, или если эта задача
окажется в
P, то PSPACE=P.
Таким образом, выбор наиболее сложных задач, для кото-
рых известно решение, и использование их в основе построения
криптосистемы, позволяет создавать практически устойчивые
шифры, раскрытие которых в принципе возможно, но для этого
потребуется столько времени, что эта процедура дешифрования
теряет практический смысл. Более подробно об этом речь пойдет
на следующих лекциях.
Задача выполнимости заключается в проверке существо-
вания выполняющего набора булевых переменных
V
1
,…,V
an
для
набора дизъюнкций (операция «или») над этим множеством эле-
ментов.
24
3. Элементы теории чисел: основные понятия и
теоремы.
В дальнейшем изложении будем использовать следующие
понятия и обозначения:
N - множество натуральных чисел: целые положительные
числа вида 1,2,…
Z - множество целых чисел: числа вида n, -n и 0, где n - на-
туральное число.
Q - множество рациональных чисел: числа вида p/q, где p и
q - целые числа и
0
≠
q
. Класс рациональных чисел включает в
себя все целые числа Z, которые в свою очередь включают в се-
бя все натуральные числа
N.
R - множество действительных чисел: этот класс включает
все рациональные числа и все числа не являющиеся таковыми
т.е. все иррациональные числа.
Рассмотрим
множество целых чисел, которые обозначим
через
Z. На множестве целых чисел рассмотрим операции сло-
жения + и умножения
×
. Операция деления, обратная операции
умножения, выполняется не для всех пар чисел из
Z. (Напомним
Z - целые числа).
Число
а делится на число b
≠
0, если существует число q
такое, что
bqaилиq
b
a
==
В этом случае говорят, что число
b делит число a.
При этом число
b - делитель числа а, число а - кратное
числа
b, число q - частное от деления а на b. Число 0 делится
на любое целое
0
≠
b
. Если
0
≠
a
, то очевидно, что множество
всех делителей числа
а конечно.
Утверждение о том, что
b делит а обозначают символом
ab/
. Если b не делит а, то этот факт обозначают ab / .
Лемма 1. Если bc/ и ab/ , то ac / .
Доказательство: по определению из bc/ и ab / имеем,

25
что
b=q
1
c, a=q
2
b, откуда а=q
1
q
2
c=qc и снова по определению
ac / .
Лемма 2. Если m=a+b, d/m и d/a, то d/a.
Доказательство: по определению m=q
1
d и a=q
2
d. Поэтому
из равенства
m=a+b получим b=q
1
d - q
2
d=(q
1
-q
2
)d=qd, откуда
следует
d/b. Отсюда следует, что если m=a
1
+a
2
+…+a
n -1
+a
n
и d
делит числа
m, а
1
,…,а
n -1
, то d/a
n
.
Общим делителем двух или нескольких чисел называется
число, являющееся делителем каждого из этих чисел.
Если а
1
,…,а
n
числа из Z и хотя бы одно из них не равно
нулю, то множество их общих делителей конечно и среди этих
делителей существует наибольшее число.
Наибольшим общий делителем (НОД) чисел а
1
,…,а
n
на-
зывается наибольший из их общих делителей. Он обозначается
(а
1
,…,а
n
).
Число
n>1 называется простым, если оно не имеет других
делителей кроме
1 и n. Например, числа 2, 3, 5, 7 являются про-
стыми, т.к. они делятся только на 1 и на самих себя.
Число n называется составным, если оно имеет делитель
отличный от 1 и
n. Например, числа 4, 6, 8 составные числа.
Если НОД
(а
1
,…,а
n
)=1, то числа а
1
,…,а
n
называют взаимно
простыми
Например: (2,5)=1; (10,21)=1
Лемма 3. Если a, b, c - целые числа, то (a, b)=1 b/ac, то b/c.
Лемма 4. Если целое число b взаимно просто с каждым из
целых чисел
а
1
,…,а
n
, то b взаимно просто с их произведением
а
1
а
2
,…, а
n
Когда
а не делится на b, то принято говорить о делении а
на
b с остатком r.
Теорема о делении с остатком. Если а и b целые числа,
то
b>0, то существуют единственные целые числа q и r такие,
что
a=b*q+r,
b
r
<
≤0
.
Число
q называют неполным частным при делении a на b,
число
r называют остатком от деления а на b.
Очевидно, что если
r=0, то b/a.
Пример.
Пусть b=12… Тогда для чисел а= 110, а= -53, а
26
=156 имеем
а=b
q+r
110=12
9+2 0<r=2<b=12
-53=12+(-5)+7 0<
r=7<b=12
156=12
13 +0 r=0
Любое натуральное составное число
n представляется в
виде
n=ab, 1<a<n, 1<b<n.
Лемма 5. Наименьший отличный от единицы делитель на-
турального числа
n>1 есть простое число.
Доказательство. Число n>1 имеет хотя бы два различных
делителя (
1 и n) и, следовательно, имеет делитель отличный от
единицы. Среди всех делителей отличных от
1 имеется наи-
меньший. Пусть это будет
q. Число q должно быть простым т.к.
в противном случае оно было бы составным и по определению
имело бы делитель q
1
такой, что 1<q
1
<q. Но q
1
/q и q/n, а тогда по
лемме1
q
1
/n. Это противоречит тому, что q наименьший дели-
тель
n, значит q - простое число.
Следствие. Каждое натуральное число n>1 имеет хотя бы
один простой делитель.
Лемма 6. Наименьший простой делитель составного числа
n не превосходит
n
.
Доказательство. Пусть p>1 наименьший делитель числа n
являющийся по лемме 5 простым числом. Так как
n составное
число, то
n=pq, где
qp
≤
. Поэтому
2
pn ≥
,откуда
np ≤
.
Лемма 7. Если p - простое число, то любое целое число а
либо взаимно простое с
р, либо делится на р т.е. р/а.
Доказательство. Наибольшим общим делителем (а, р) чи-
сел
а и р может быть только делитель простого числа р, который
в свою очередь может быть равен
1 или р. тогда в первом случае
(а, р)=1 и числа а и р взаимно простые, а во втором случае когда
(а, р)=р а делится на р т.е. р/а.
Основная теорема арифметики. Любое натуральное чис-
ло
n>1 представляется в виде произведения простых чисел, при-
чем единственным образом.
Доказательство. По лемме 5 число n>1 имеет наимень-
ший простой делитель
р
1
. тогда n=p
1
a
1
. Если а
1
>1, то аналогично

27
получим
а
1
=р
2
а
2
, где р
2
наименьший простой делитель числа
а
1
>1. Т.к. числа а
1
, а
2
,… убывают, то на некотором r шаге будем
иметь
a
r -1
=p
r
a
r
где a
r
=1 т.е. a
r -1
=p
r
.
Перемножая все полученные таким образом равенства по-
сле сокращения на а
1
, а
2
,…a
r -1
получим разложение числа n на
простые сомножители
n= p
1
p
2
…
p
r
Пусть
n>1 и оно представлено в виде разложения на про-
стые сомножители
n= p
1
p
2
…
p
r
Среди чисел p
1
,…,p
r
могут быть одинаковые. Пусть p
1
,…,p
к
различные из чисел p
1
,…,p
r
(r>k), a
α
1
,…,
α
k
кратности с которы-
ми они входят в исходное разложение. Тогда это разложение
можно записать в виде:
⎩
⎨
⎧
−
−
⋅⋅⋅=
числацелые
простоеp
pppn
i
i
k
k
, ...
2
2
1
1
α
ααα
,
который называется
каноническим разложением числа n
на простые множители.
Пример
234
11532261360 ⋅⋅⋅
=
.
Согласно теореме Евклида: Множество простых чисел бес-
конечно.
Для того, чтобы составить таблицу всех простых чисел
можно использовать метод, называемый решетом Эратосфена
(древне - греческий математик).
Напишем одно за другим числа 2,3,…
N
Число 2 является простым оставляем и зачеркиваем после
него все числа кратные 2 т.е. все четные числа. Следующим за
числом 2 является число 3, которое является простым. Оставля-
ем 3, зачеркиваем все числа кратные 3. Продолжая этот процесс,
находим все простые числа, не превышающие заданного числа
N.
Например,
N=40: 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Простые числа: 2,3,5,7,11,13,17,19,23,29,31,37
Построение в настоящие время таблицы простых чисел по-
казывают, что с ростом их величин они встречаются все реже и
28
реже. Например, в первой сотне чисел (
N=100) их 25, во второй -
21, третьей 16 и т.д. В первой 1000 их 168, во второй тысяче -
135, в третьей - 120 и т.д. Особый класс простых чисел состав-
ляют числа вида 21
n
−
. Такие числа называют простыми чис-
лами Мерсенна и они являются наибольшими по своему разме-
ру среди других известных простых чисел. Во времена Эйлера
наибольшим простым числом было пятое число Мерсенна 2
31
-1.
Через сто лет было найдено шестое число Мерсенна 2
61
-1. В
1992 найдено самое большое известное число -32 число Мерсен-
на. Его запись содержит 227 832 цифры и требует около ста
страниц текста.
Простые числа распределены в натуральном ряде чисел
очень нерегулярно. Согласно основной теоремы арифметики,
простые числа являются теми простейшими объектами, из кото-
рых с помощью умножения строятся все натуральные числа
большой единицы
. Поэтому вопросы, связанные с распределе-
нием простых чисел являются важнейшими в теории чисел. Для
того была введена функция П(х) выражающая число простых
чисел
≤
х. Известно, например, что П(1)=0, П(2)=1, П(10)=4,
П(40)=12… . Однако для функции П(х) неизвестно никакой про-
стой формулы, позволила бы изучать её поведение. Существуют
определенные оценки для функции П(х) (оценки Чебышева, тео-
ремы об асимптотическом законе распределении простых чисел
Римана и другие). По мере необходимости в дальнейшем мы бу-
дем использовать эти результаты. Наряду с этим в теории чисел
уделяется большое внимание решению аддитивных задач, свя-
занных с возможностью предоставления натуральных чисел в
виде суммы простых чисел. Наиболее известная
из таких задач -
проблема Гольдбаха (1742 г.). Гольдбах в письме к Л. Эйлеру
высказал предположение, что всякое нечётное число большее 6
можно представить в виде суммы трех простых чисел. Эйлер в
свою очередь высказал более сильную гипотезу: всякое число,
начинающееся с 4 можно представить в виде суммы двух про-
стых чисел. Первым результатом, связанным
с этой проблемой
была теорема о том, что существует постоянная
к такая, что ка-
ждое натуральное число большее единицы есть сумма не более
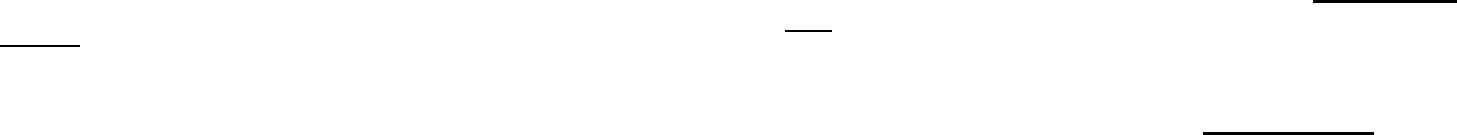
29
чем
к простых чисел. Далее была доказана теорема (Виноградов
И.М.), утверждающая что всякое достаточно большое нечетное
число представимо в виде суммы трех простых чисел.
Утверждение о представлении четных чисел в виде суммы
двух простых чисел до сегодняшнего дня не доказано.
Продолжим знакомство с основными понятиями и теоре-
мами теории чисел, которые
будут необходимы для дальнейше-
го изложения лекционного курса.
Пусть
m
∈
N - натуральные числа.
Целые числа
а и b (a,b
∈
z) называются сравнимыми по мо-
дулю
m
∈
N (m
≠
0) если разность a и b делится на m т.е. m/a-b.
Сравнимость чисел
a и b по модулю m обозначают симво-
лом
),(mo
d
mba ≡
называемым сравнением по модулю m.
Числа
a и b сравнимы по модулю m тогда и только тогда,
когда существует целое
t(t
∈
z) такое, что
,m
t
ba
+
=
также и
только тогда, когда они имеют одинаковые остатки при делении
на
m т.е.
12
; .amq r bmq r=+ =+
Отсюда следует, что все целые числа Z по модулю m раз-
биваются по
m непересекающихся классов сравнимых между
собой чисел (т.е. имеющих одинаковые остатки при делении на
m)
Каждое число
b, входящее в какой - либо из классов, назы-
вается
вычетом числа a по модулю m, а каждый класс - классом
вычетов по модулю m. Число разных классов вычетов равно m.
Полной системой вычетов (по модулю
m) называют мно-
жество из
m целых чисел {
m
rr ,...,
1
}, если для любого целого
числа
a существует точно одно число
),...,1 ( mir
i
=
из мно-
жества
},...,{
1 m
rr такое, что
)(mod mra
i
=
.
Пример
: множество {0,1,2,…m -1}
Сравнимость по модулю
m для произвольных целых, чисел
является отношением эквивалентности, (т.е. классы вычетов по
модулю
m являются классами эквивалентности) т.к. для них
30
справедливо выполнение соотношений:
(mod )
(mod ) (mod )
(mod ), (mod ) (mod )
a a m ðåô ëåêñèâí î ñò ü
ab m ba m ñèììåòðè÷íîñòü
ab m bc m ac m
òðàíçèòèâíîñòü
≡
−
≡→≡−
≡≡→≡
−
Свойства сравнений по модулю
m напоминают свойства
обычных числовых равенств:
1. Два числа, сравнимые с третьим, сравнимыми между
собой
2. Сравнения по одному и тому - же модулю можно по-
членно складывать:
)(mod)](mod)(mod[)(mod
2121
mmamamaa
⋅
+
=
+
3.
Сравнения по одному и тому - же модулю можно по-
членно перемножать:
)(mod)](mod)(mod[)(mod
2121
mmamamaa
⋅
⋅
=
⋅
Правила сокращения сравнений несколько отличаются от
правил сокращения неравенств.
4.
Если
)(mo
d
, 1), () (mo
d
mV
U
тоmaиmaVaU
≡
=
≡
(mod ), (mod ).
Å
ñëè aU aV am ò î U V m
=
≡
Для каждого целого числа
m, m>1 ввести числовую функ-
цию
ϕ
(m), представляющую собой количество чисел из сово-
купности чисел
0,1,…,m -1 взаимно простых с m. Функцию
ϕ
(m) называют функцией Эйлера. Например:
ϕ
(2)=1,
ϕ
(3)=2,
ϕ
(4)=2,
ϕ
(5)=4,
ϕ
(6)=2 и т.д.
Очевидно, что если
m=p - простое число, то
ϕ
(p)=p-1. На-
звание функции
ϕ
(m) происходит из следующей теоремы Эй-
лера: Для любых целых чисел а и m, таких, что (a,m)=1 (т.е. a и
m взаимно простые числа) справедливо выражение
).(mod1
)(
ma
m
≡
ϕ
Из теоремы Эйлера следует малая
теорема Ферма: Если р

31
- простое число и
ap / , то
)(mod1
1
pa
p
≡
−
. Это утверждение
очевидно, если вспомнить, что для простого числа р,
() 1pp
ϕ
=−
.Наименьшие из чисел
:1(mod),(,)1amam
γ
γ
≡
=
называется
показателем числа а по модулю m. Существование
таких чисел
γ
обеспечивается указанной выше теоремой Эйле-
ра. Если показатель числа
а по модулю m равен
δ
, то
(mod )aa m
γβ
≡
тогда и только тогда, когда
(mod )
γ
βδ
=
. Показа-
тель числа
а по модулю m является делителем числа
()m
ϕ
. Ес-
ли показатель числа
a по модулю m равен
δ
, то показатель числа
a
k
равен
(,)
Í
ÎÄ k
δ
δ
для произвольного целого k. В частном слу-
чае, когда показатель числа
а по модулю m равен
ϕ
(m), то а на-
зывается
первообразным (примитивным) корнем по модулю m.
Если
р – простое число, и число а является первообразным кор-
нем по модулю
Р, то любой элемент b из множества чисел
1,2,…,р -1 имеет однозначное представление в виде
(mod )
x
ba P≡
для некоторого целого числа х
∈
{0,1,…,р -1}.
Число
х при этом называется дискретным логарифмом
(или
индексом) числа b по основанию а.
Сложность вычисления дискретных логарифмов совпадает
со сложностью нахождения разложения целого числа на простые
сомножители и имеют
exp сложность, что определяет широкое
применение таких задач при построении современных криптоси-
стем
Число
m называется псевдослучайным по основанию а, ес-
ли
1
1(mod )
m
ap
−
≡ и
(, ) 1am =
(р – простое число). Существуют
составные числа
m, являющиеся псевдослучайными для всех а,
взаимно простых с
m. Такие числа называются числами Кар-
майкла. Например,
561 3 11 17, 1105 5 13 17mm
=
=⋅ ⋅ = =⋅ ⋅ . Если t
различных оснований
а
1
,…,а
t
выбираются независимо и случай-
но, то составное число
m выдержит тест Ферма
1
1(mod )
m
am
−
≡
i=1,…,t с вероятностью 2
t
p
−
≤ .
Важное значение в теории чисел и для дальнейшего изло-
32
жения материалов лекционного курса имеет понятие многочлена
или полинома.
Многочленом называется выражение вида
2
01 2
0
() ...
n
ni
ni
i
f
xaaxax ax ax
=
=+ + ++ =
∑
0
i
ãäå a i n
≤
≤ - коэффициенты;
х – переменная;
n - степень многочлена, обозначаемая degf(x).
Для многочленов, также как и для чисел, могут быть вве-
дены арифметические операции. Два многочлена
∑
=
=
n
i
i
i
xaxf
0
)(
и
∑
=
=
n
i
i
i
xbxg
0
)(
равны тогда и только тогда, когда
ii
ba =
.
Сумма многочленов
f(x) и g(x) определяется равенством
∑
=
+=+
n
i
i
ii
xbaxgxf
0
,)()()(
а произведение
∑∑
==
==
m
i
n
j
j
j
i
i
xbxgиxaxf
00
)( )(
∑∑
=+
+
=
==⋅
kji
jik
nm
k
k
k
bacгдеxcxgxf ,)()(
0
.
Теорема. Пусть f(x) и g(x) многочлены, тогда
)).(deg())(deg())()(deg(
)))(deg()),(max(deg())()(deg(
xgxfxgxf
x
g
x
f
x
g
x
f
+=⋅
≤
+
.
Многочлен
f(х) делится на многочлен g(x), если существу-
ет многочлен
q(x) такой, что f(x)=q(x)g(x).
В этом случае говорят, что многочлен
g(x) делит много-
член
f(x), при этом g(x) - делитель многочлена f(x), а f(x) -
кратное многочлена g(x).
Для многочлена
f(x)=a
0
+a
1
x+…+a
n
x
n
коэффициент а
0
явля-
ется
постоянным членом т.е. константой. Многочлены степени
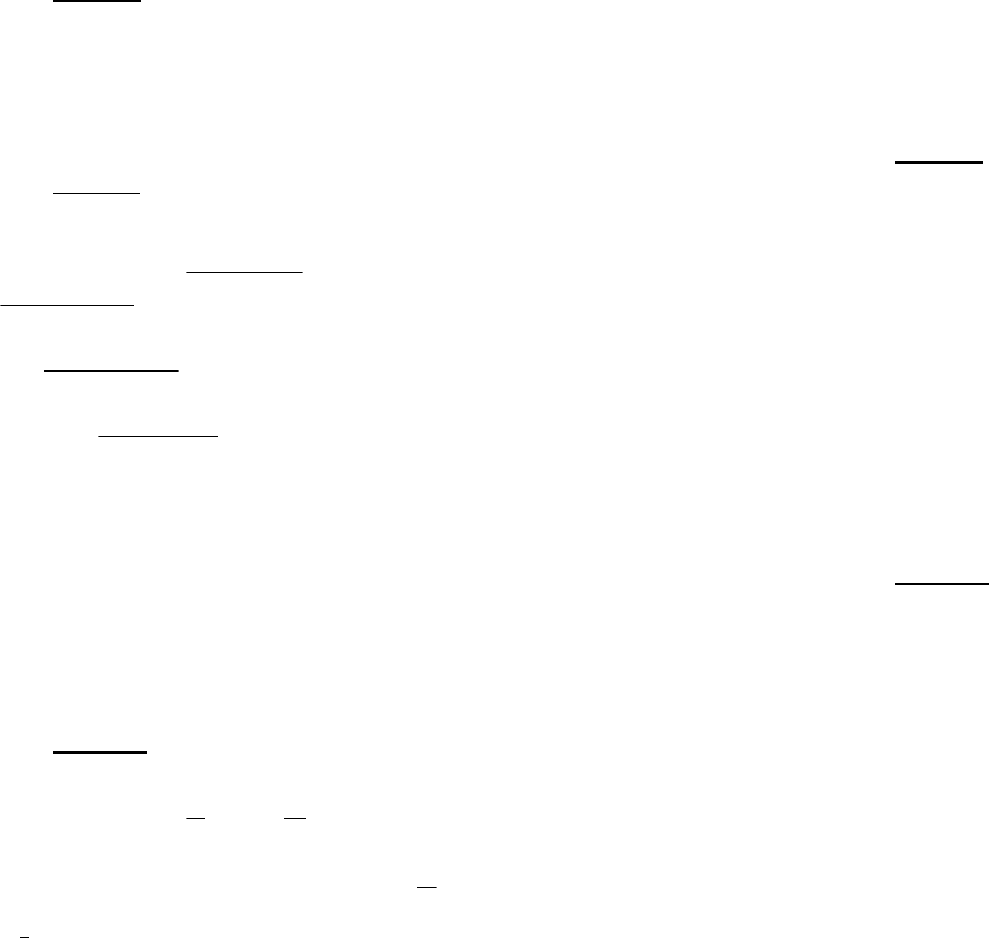
33
0≤n
называются постоянными многочленами - константами.
Теорема (алгоритм деления многочленов с остатком)
Пусть
g(x)≠0 некоторый многочлен. Тогда для каждого
многочлена
f(x) существует также многочлены q(x) и r(x), что
() () () ()
deg( ( )) deg( ( ))
fx qxgx rx
ãäå r x g x
=+
<
Пример:
1)(
)(
23
36
++=
+=
xxxg
xxxf
63 32
653 32
5
542
42
43
32
| 1
1()
xx xx
x
xx xxx qx
x
xxx
xx
xxx
xxx
+++
++ +++=
++
+
++
++
))(deg())(deg(
x
g
x
r
<
32
xxx++
)(1
x
r
x
=+
Пусть
f(х) – многочлен с целыми коэффициентами. Срав-
нение вида
f(х)≡0(mod m) называется сравнением с неизвестной
величиной. Задача о решении сравнения с неизвестной величи-
ной состоит в отыскании всех значений
х, которые ему удовле-
творяют.
Простейшее линейное сравнение имеет вид
ax
≡
b(mod m),
(
a,m)=1.
Теорема. Пусть d=НОД(a,m). Если d/b, то сравнение
ax
≡
b(mod m) будет иметь d решений вида:
,1,...,1,0 , mod))()((
0
−=+= dtm
d
m
tx
d
b
x
где
0
x - решение сравнения
)(mod1)( mx
d
a
=
. Если
bd
/
, то решений нет.
34
Пусть
n
n
xaxaaxf +++= ...)(
10
- многочлен с целы-
ми коэффициентами
).,...,1,0( niZa
i
=
∈
Два решения
21
xиx сравнения n -ой степени )(mo
d
0)( m
x
f
≡
называют-
ся
эквивалентными, если
)(mod
21
mxx
≡
. Числа решений
сравнения определяется числом неэквивалентных решений.
Теорема. Пусть
r
mm ,...,
1
- попарно взаимно простые чис-
ла (т.е.
НОД(
ji
mm , )=1 для n
j
i ≤
<
≤
1 ) и
r
mmmm
⋅
⋅
⋅
= ...
21
. Тогда справедливо:
1.Сравнение
)(mod0)( m
x
f
≡
равносильно системе срав-
нений
)(mod0)(),...,(mod0)(
1 r
mxfmxf
≡
≡
2.Число решений сравнения
)(mo
d
0)( m
x
f
≡
равно про-
изведению числа решений отдельных сравнений указанной в п.1.
системы сравнений.
По аналогии с целыми числами можно ввести понятия
наибольшего общего делителя многочленов, наименьшего об-
щего кратного многочленов, взаимно простых и попарно вза-
имно простых многочленов, отношение сравнимости много-
членов и ряд других важнейших понятий.
Теорема. )(),...,(
1
xfxf
n
- многочлены, не все равные ну-
лю. Тогда существует однозначно определенный нормативный
многочлен
d(x), обладающий свойствами
1.
d(x) делит каждый многочлен
nixf
i
,...,1) , (
=
.
2.Любой многочлен
g(x), который делит каждый из много-
членов
),...,1), (( nixf
i
=
, делит и многочлен d(x).
Нормированный многочлен
d(x) называют наибольшим
общим делителем многочленов )(),...,(
1
xfxf
n
и обозначают
НОД( )(),...,(
1
xfxf
n
). Если НОД( )(),...,(
1
xfxf
n
)=1, то мно-
гочлены
)(),...,(
1
xfxf
n
называются взаимно простыми. Они
называются
попарно взаимно простыми, если
njixfxfНОД
ji
≤
<
≤
=
1, 1))(),((
.

35
Наибольший общий делитель двух многочленов (также как
и двух целых чисел) можно найти при помощи алгоритма Евк-
лида. Пусть многочлен
g(x)
≠
0 и не делит многочлен f(x).
Тогда, применяя многократно алгоритм деления многочле-
нов с остатком, получим
11 1
21 2 2 1
1323 3 2
21
( ) ( ) ( ) ( ) 0 deg( ( )) deg( ( ))
() ()() () 0 deg( ()) deg(())
() () () () 0 deg( ()) deg( ())
() () () () 0 deg(
SSSS S
fx g xgx rx rx gx
gx g xrx rx rx rx
rx g xrx rx rx rx
rxgxrxrx r
−−
=+≤<
=+ ≤<
=+≤<
•
•
•
=+≤
1
11
()) deg( ())
() () ()
S
SSS
x
rx
rxg xrx
−
−+
<
=
Т.к. степень
deg(g(x)) конечна, то процедура заканчивается
за конечное число шагов. Если старший коэффициент последне-
го ненулевого остатка
)(xr
S
равен b, то
)())(),((
1
xrbxgxfНОД
S
−
=
.
Если у нас более чем 2 многочлена
(n>2), то
НОД( )(),...,(
1
xfxf
n
) при ненулевых многочленах
)(),...,(
1
xfxf
n
находят (как и для целых чисел), применяя рас-
ширенный алгоритм Евклида: сначала определяют
НОД( )(),(
21
xfxf ), а затем находят последовательно, применяя
алгоритм Евклида,
НОД(НОД( )(),(),(
321
xfxfxf ))=НОД( )(),(),(
321
xfxfxf ) и
т.д.
Пример:
xxxxg
xxxxf
++=
+++=
24
236
)(
1)(
Найдем
НОД( )(),(
x
g
x
f
) по алгоритму Евклида
1)1(1
1)1()1(
1)()1(1
2324
242236
⋅+=+
++⋅++=++
++++⋅+=+++
xx
xxxxxx
xxxxxxxx
36
Значит,
НОД( )(),(
x
g
x
f
)=1 т.е. многочлены f(x) и g(x)
взаимно простые.
Двойственным к понятию
НОД является понятие наи-
меньшего общего кратного. Пусть )(),...,(
1
xfxf
n
- ненулевые
многочлены. Тогда можно показать, что существует однозначно
определенный нормированный многочлен
m(x), обладающий
следующими свойствами:
1.
m(x) делится на каждый многочлен
) ,...,1), (( nixf
i
=
;
2. любой многочлен
g(x), который делится на каждый из
многочленов
) ,...,1), (( nixf
i
=
делится на m(x).
Многочлен
m(x) называют наименьшим общим кратным
многочленов
)(),...,(
1
xfxf
n
и обозначается
НОК )(),...,(
1
xfxf
n
. Для двух многочленов
0)( 0)(
≠
≠
x
gи
x
f
имеет место соотношение
))(),(())(),(()()(
1
xgxfНОКxgxfНОДxgxfa =⋅⋅
−
,
где а - старший коэффициент произведения
f(x) и g(x).
Важнейшим понятием теории чисел является понятие не-
приводимого многочлена. Многочлен
f(x) называется неприво-
димым, если он имеет положительную степень и равенство
f(x)=g(x)h(x) может выполняться лишь в том случае, когда либо
g(x), либо h(x) является постоянным многочленом (т.е. его сте-
пень
0
≤
n ). Другими словами, многочлен f(x) является непри-
водимым, если он допускает только тривиальные разложения на
множители.
Многочлен положительной степени
f(x) называется приво-
димым, если существуют два многочлена положительной степе-
ни
)( ) (
21
xfиxf такие, что )()()(
21
xfxfxf
⋅
=
, т.е. если
этот многочлен
f(x) не является неприводимым.
Неприводимые многочлены играют важную роль в теории
чисел, так как любой многочлен
f(x) может быть записан, при-
чем единственным способом, в виде произведения неприводи-
мых многочленов (аналог того, что любое число
n>1 может быть
представлено в виде произведения простых чисел).

37
Лемма: Если неприводимый многочлен f(x) делит произведение
многочленов
)(),...,(
1
xfxf
n
, то по крайней мере один из со-
множителей
) ,...,1), (( nixf
i
=
делится на f(x).
Используя эту лемму, можно сделать следующее фунда-
ментальное утверждение:
Теорема. (об однозначном разложении на множители)
Каждый многочлен положительной степени f(x) может
быть представлен в виде произведения
K
l
k
l
fxfaxf ⋅⋅⋅= ...)()(
!
1
,
где
а старший коэффициент f(x); )(),...,(
1
xfxf
k
- различ-
ные нормированные неприводимые многочлены;
k
ll ,...,
1
- нату-
ральные числа
1,2,….
При этом такое разложение называют
каноническим раз-
ложением многочлена.
Наиболее интересные и важные свойства объектов (чисел,
многочленов и др.) теории чисел, которые потребуются в даль-
нейшим, получены и описаны, в частности, в рамках теории ко-
нечно поля. Поэтому в дальнейшем рассмотрим элементы тео-
рии конечного поля.
38
4. Элементы конечного поля. Основные понятия и
свойства алгебраических структур.
Группы
Известны две операции на множестве Z целых чисел: сло-
жение и умножение. Обобщим понятие операции на произ-
вольное множество. Пусть
S - некоторое множество и пусть
SS ⋅ обозначает множество упорядоченных пар (s,t) , где Ss ∈ и
St ∈ . Тогда произвольное отображение из SS
⋅
в S будем назы-
вать
операцией (бинарной) на множестве S. В этом определе-
нии потребуем, чтобы образ каждой пары, был непременно эле-
ментом множества
S. Это так называемое свойство замкнуто-
сти операции. Под алгебраической структурой или системой
будем понимать некоторое множество
S с одной или нескольки-
ми операциями на нем. Одной из таких алгебраических структур
с одной операцией является
группа.
Определение. Группой (G,*) (в дальнейшем группу будем
называть просто
G) называется некоторое множество G c бинар-
ной операцией
* на нем, для которых выполняются следующие
условия:
1. Операция
* ассоциативна, т.е. для любых а,b,c,
∈
G
справедливо
a*(b*c)=(a*b)*с.
2. В
G существует единичный элемент (или единица) е та-
кой, что для любого
а
∈
G
а*е = e*a = a
3. Для каждого а
∈
G существует обратный элемент a
-1
∈
G,
такой что
a * a
-1
= a
-1
* a = e
Если группа
G удовлетворяет также следующему условию:
для любых
а,b
∈
G справедливо
а*b=b*а ,
то она называется коммутативной или абелевой группой.
Единичный
e и обратный а
-1
элемент группы G для каждо-
го данного элемента
а
∈
G определяется однозначно указанными
выше условиями. Для всех элементов
а,b
∈
G имеет место ра-
венство
(a*b)
-1
= b
-1
*a
-1
. Для групповой операции * может быть

39
использовано мультипликативное обозначение, как для обычно-
го умножения. Тогда вместо
а*b можно просто записать а
⋅
b или
аb . Однако при этом не предполагается, что операция * -это
простое умножение. В ряде случаев для групповой операции
*
может быть использована аддитивная запись
а+b вместо а*b.
Тогда элемент группы
G а+b называют суммой элементов а,b и
0 вместо е (единичный элемент в мультипликативной записи ) и
-а вместо a
-1
. Такие обозначения обычно используются для абе-
левых групп.
Если
а
∈
G и n
∈
N в мультипликативной записи пишут a
n
= a
⋅
a ... a (n сомножителей a) и элемент a
n
называют n
й
степе-
нью числа
а.
Если для групповой операции используется
+ т.е. аддитив-
ное обозначение, то вместо
a
n
будем иметь nа=а + а + ... + а (n
слагаемых
а).
Используя мультипликативные и аддитивные обозначения
в общем случае имеем следующие правила:
Мультипликативные
обозначения
Аддитивные
обозначения
a
-n
= (a
-1
)
n
( -n)а=n( -а)
a
m
a
n
= a
m+n
mа+nа=(m+n)а
(a
m
)
n
= a
m
⋅
n
m(nа)=(m
⋅
n)а
Для n=0
∈
Z имеем
a
0
= e в мультипликативных обозначениях и 0
⋅
а=0 в адди-
тивных обозначениях.
Группы
G, использующие указанные формы записи назы-
вают
мультипликативными и аддитивными.
Примеры.
1)
Пусть G - множество целых чисел с операцией + (сло-
жение). Известно, что данная операция, т.е. сумма двух целых
чисел однозначно определяет целое число. Эта группа
G, еди-
ничным элементом которой является
0, а обратным для целого
числа
а является число -а . Такую группу обозначают через Z.
2)
Множество, состоящее из единственного элемента е с
операцией
* , определенной условием е*е=е является группой.
Определение. Мультипликативная группа G называется
40
циклической, если в ней имеется такой элемент а , что каждый
элемент
b
∈
G является степенью элемента а т.е. существует це-
лое число
К такое, что b = a
K
. Этот элемент а называется обра-
зующим элементом группы G . Для циклической группы G
применяют обозначение G=<а>.
Из определения следует, что циклическая группа является
коммутативной или абелевой.
В аддитивной циклической группе
Z b=ка может быть бо-
лее одного образующего элемента, например
1 и –1.
Отношением эквивалентности на множестве S называ-
ется подмножество
R множества S
×
S упорядоченных пар (s,t)
s,t
∈
S обладающее тремя свойствами:
1.
(s,s)
∈
R для всех s
∈
S (рефлективностью)
2. Если
(s,t)
∈
R , то (t,s)
∈
R (симметричностью)
3. Если
(s,t) ,(t,v)
∈
R, то (s,v)
∈
R (транзитивностью)
Элементы
s,t
∈
S называются эквивалентными, если
(s,t)
∈
R. Простейшим примером отношения эквивалентности яв-
ляется равенства
s=t:
1. s=s, t=t
∈
R
2. s=t → t=s ∈ R
3. s=t, t=v → s=v ∈ R
Отношение эквивалентности на множестве S разбивает это
множество
S на попарно непересекающиеся подмножества, объ-
единяя все элементы множества
S, эквивалентные некоторому
фиксированному элементу
s
∈
S получим класс эквивалентности
элемента
s, который обозначается:
[s]={t
∈
S
|
(s,t)
∈
R}.
Совокупность всех различных классов эквивалентности да-
ет указанное выше разбиение множества
S на попарно непересе-
кающиеся подмножества (
классы эквивалентности).
Как уже отмечалось на прошлой лекции, важным классом
эквивалентности на множестве целых чисел является отношение
сравнимости чисел
а и b (a,b
∈
z) по модулю n. a
≡
b(mod n).
Классы эквивалентности, на которые отношение сравнимо-
сти по модулю
n разбивает множество целых чисел Z, называют
классами вычетов по модулю n. Ими являются:
