Furusawa A., van Loock P. Quantum Teleportation and Entanglement: A Hybrid Approach to Optical Quantum Information Processing

Подождите немного. Документ загружается.

300 8 Hybrid Quantum Information Processing

example, for CV quantum teleportation of DV states), the standard way of apply-

ing such methods has to be generalized. In particular, frequency-resolved homo-

dyne detection, as used, for instance, in CV quantum teleportation of coherent

states [203], must be extended to time-resolved homodyning in order to synchro-

nize the CV operations with DV photon counting events. CV operations must act

on a faster scale: while the standard CV experiments used single-mode cw light

sources with narrow sidebands of 30 kHz, the new generation of hybrid experi-

ments relies upon bandwidths of at least 100 MHz, corresponding to time scales

of 100 ns.

For example, in order to teleport a coherent-state superposition (a so-called cat

state) using a CV Gaussian EPR resource, the successful photon events that indi-

cate the presence of a cat state at the input of the teleporter must be synchronized

with those shots that deﬁne successful quantum teleportation events. For this pur-

pose, time-domain EPR correlations are needed (see Section 3.2.3.2). This new gen-

eration of experiments is accompanied by a paradigm shift, which is necessary in

order to combine the complementary wave and particle properties of light. Thus

far, experiments have focused either on the particle aspect, using photon coun-

ters and postselection, or on the wave aspect, measuring quadratures in phase

space. The former type of experiments were always conditional and hence high-

ly inefﬁcient; even worse, in many schemes, there was no way to actually obtain

a physical state at the output for further exploitation. The CV quadrature-based

experiments were typically performed in the frequency-domain with no time res-

olution. For those new hybrid approaches to work, the domain must be shifted

from frequency to time, and measurements from (power) statistics to (amplitude) single

shots.

In this chapter, we shall ﬁrst discuss a couple of protocols for the optical en-

gineering of non-Gaussian cat states (Section 8.1). Subsequently, we describe an

experiment in which such a cat state was optically generated from squeezed light

through photon subtraction techniques (Section 8.2). In Section 8.3, we introduce

some examples of hybrid entangled states, and in Section 8.4, we describe two (hy-

brid) teleportation experiments: one in which a cat state is prepared and then, to

some extent, transferred through quantum teleportation (Section 8.4.1); and an-

other one where a DV polarization-encoded photonic qubit is teleported using CV

EPR resources and CV Gaussian operations (S ection 8.4.2). Finally, we present a

few speciﬁc hybrid approaches to quantum computing (Section 8.5), including the

notion of hybrid Hamiltonians (Section 8.5.1), speciﬁc ways to encode qubits into

qumodes (Section 8.5.2), and, in Section 8.5.3, the famous proposal by Gottesman,

Kitaev, and Preskill (GKP).

8.1

How to Create Non-Gaussian States, Cat States

Coherent states may be used to encode a photonic qubit state in a qualitative-

ly different way compared to the photon number and polarization encodings of

8.1 How to Create Non-Gaussian States, Cat States 301

Chapter 2,

(

ajαiCbjαi

)

N(α), (8.1)

with N(α) Djaj

Cjbj

C 2e

2jαj

Re(ab



). A proof-of-principle proposal of such

cat states for fault-tolerant, universal quantum computation was presented in [308].

This proposal describes an all-optical scheme using photon number resolving de-

tectors. Although in theory, cat states can be produced directly from χ

(3)

nonlin-

ear optical interactions, their generation becomes more feasible when conditional

state preparation is allo wed. A drawback of the cat-type qubit encoding is that these

states are fairly sensitive to losses and noise. Below, we shall describe a protocol for

cat-state engineering that is not all-optical and uses light-atom interactions.

In the all -optical approaches, there are currently various schemes which often re-

ly upon the resemblance of squeezed Fock states and photon-subtracted, squeezed

vacuum states with a cat state,

jαijαi

S(r)j1iOa

S(r)j0i . (8.2)

This is the so-called odd cat state that only has odd photon-number terms, as one

can easily understand from the Fock expansion of the coherent states. In fact, we

mayapproximatelywrite

S(r)j1iD

nD0

tanh

cosh

3/2

(2n C 1)!

j2n C 1i . (8.3)

The above approximation hol ds with near-unit ﬁdelity for near-unit or smaller am-

plitudes α. The even cat state is correspondingly /jαiCjαi,withonlyeven

number terms.

A beautiful example of a typical hybrid scheme according to our deﬁnition is

the “ofﬂine squeezing” protocol from [279] for cat-state engineering, experimental-

ly demonstrated in [309], see Figure 8.1. In this scheme, approximate cat states are

built using linear CV measurements with outcomes within a ﬁnite postselection

window, linear CV squeezed-state, and nonlinear DV Fock-state resources. The pro-

tocol works by squeezing the input Fock state, j1i!

S(r)j1ijαijαi.This

squeezing would be hard to achieve “online” directly on the Fock state using the

standard squeezing techniques such as optical parametric ampliﬁcation.

Let us discuss yet another way to create cat states, this time using light-atom

interactions [310]. In Chapter 1, we introduced the qubit Pauli operator basis X, Y,

and Z as elementary gates, and rotations along their respective axes, Z

,andso

on, to describe and realize arbitrary single-qubit unitaries. In analogy, we used a

similar notation for the qumode WH operator basis, X(τ)andZ(τ). Here, in the

hybrid context, we shall exploit interactions and operations involving combinations

1) In the experiment of [309], a two-photon state jn D 2i was simply split at a beam splitter;

therefore, the squeezed vacuum in Figure 8.1 was just a vacuum state. Postselection through

time-resolved homodyne detection led to an output cat state which was squeezed by 3.5 dB.

Theoretically, the ﬁdelity of the cat state would approach unity for input Fock states jni with

n !1[309].

302 8 Hybrid Quantum Information Processing

out

)(

Figure 8.1 Conditional preparation of an odd (even) cat state using DV

one-photon (two-photon) Fock states, jψ

iDj1i (jψ

iDj2i)and

CV squeezed vacuum resources,

S(r)j0i, together with CV homodyne

detection and postselection [279].

of DV qubit and CV qumode operators and therefore we prefer to use unambiguous

notations: for qumodes, still X(τ) D exp(2iτ Op)andZ(τ) D exp(2iτ Ox)fortheWH

group elements, and Ox and Op for the Lie group generators with Oa DOx C i Op;for

qubits, now σ

 X , σ

 Y ,andσ

 Z for the Pauli basis.

Now, consider the effective interaction obtainable from the fundamental Jaynes–

Cummings Hamiltonian, „g( Oa

†



COaσ

), in the dispersive limit [311],

int

D„χσ

†

Oa . (8.4)

Here, Oa ( Oa

†

) refers to the annihilation (creation) operator of the electromagnetic

ﬁeld qumode in a cavity and σ

Dj0ih0jj1ih1j is the corresponding Pauli operator

for a two-level atom in the cavity (with ground state j0i and excited state j1i). The

atomic system may as well be an effective two-level system with an auxiliary level

(a so-called Λ-system).

The operators σ

and (σ



) are the raising (lowering) operators of the qubit. The

atom-light coupling strength is determined by the parameter χ D g

/∆,where2g

is the vacuum Rabi splitting for the dipole transition and ∆ is the detuning between

the dipole transition and the cavity ﬁeld. The Hamiltonian in Eq. (8.4) generates a

controlled phase-rotation of the ﬁeld mode depending on the state of the atomic

qubit. This can be written as (θ D χt)

R(θσ

) D exp



iθσ

†



, (8.5)

which describes a unitary operator that acts in the combined Hilbert space of a

single qubit and a single qumode. We may apply this operator upon a qumode in a

coherent state, and may formally write

R(θσ

)jαiDjα exp(iθσ

)i . (8.6)

The qumode acquires a phase rotation depending on the state of the qubit, see

Figure 8.2. As the eigenvalues of σ

are ˙1, applying

R(θσ

) to the initial qubit–

qumode state jαi˝

(

j0iCj1i

)

2resultsin

jα exp(iθσ

)i˝

(

j0iCj1i

)



αe

iθ

j0iC

αe

iθ

j1i



2, (8.7)

a hybrid entangled state between the qubit and the qumode.

The observation that this hybrid entangled state can be used for creating a macro-

scopic superposition state of a qumode, a cat state, by measuring the microscopic

system, the qubit, is about 20 years old [310]. A suitable measurement is a pro-

8.2 Experiment: Creation of Non-Gaussian States, Cat States 303

−

Figure 8.2 Controlled phase rotation of a qumode in a coherent state,

α real. Depending on the qubit state, σ

D˙1,thephaseangleofthe

controlled rotation will be θ . When the qubit starts in a superposition

state, /j0iCj1i, we obtain a hybrid entangled state between the qubit

and the qumode.

jection onto the conjugate σ

qubit basis, fj˙ig,equivalenttoaHadamardgate

applied to the qubit,



αe

iθ

jCi C

αe

iθ

ji



2, (8.8)

followed by a qubit computational σ

measurement. Depending on the result, we

obtain /jαe

iθ

i˙jαe

iθ

i for the qumode. The size of this cat state depends on

the distance between the rotated states in phase space, see Figure 8.2, scaling as

αθ for typically small θ values. However, sufﬁciently l arge initial amplitudes α

still lead to arbitrarily “large” cat states (while at the same time increasing their

vulnerability against photon losses).

In the next section, we will describe a cat-state engineering experiment using

photon subtraction. Let us mention that another method using photon counting,

namely, “photon-addition”, that is, in the ideal case, applying the photon creation

operator, serves a similar role in recent hybrid experiments [312].

8.2

Experiment: Creation of Non-Gaussian States, Cat States

In this section, we shall describe the creation of Schrödinger kitten states as experi-

mentally demonstrated by Wakui et al. [313]. This experiment is a hybrid scheme in

the sense that an exotic, non-Gaussian CV qumode state is conditionally prepared

from an unconditional source of Gaussian squeezed vacuum using DV photon sub-

traction measurements. Such heralded qumode states are interesting candidates

for testing the power of CV processing of DV encoded quantum information, for

instance, through CV quantum teleportation using the broadband (time-domain)

entangled states presented in Section 3.2.3.2.

As we have encountered throughout this book, with regards to universal pro-

cessing and so also for conditional state preparation, a sufﬁciently strong nonlin-

earity can be induced even on the single-photon level by suitable measurements.

Various nonclassical states can be generated, for instance, through photon count-

ing on a subsystem of an entangled state produced by parametric down conver-

sion [314, 315]. States produced this way could be, for example, photon number

states or Schrödinger-cat states. The nonclassicality of such states is related with

negative regions of a phase-space distribution function such as the Wigner func-

tion. This is in contrast to the Wigner function of a squeezed state, which is Gaus-

sian and thus non-negative. Here, for the present discussion of the experiment of

304 8 Hybrid Quantum Information Processing

Wakui et al. [313], we recall that the Wigner function can be directly reconstructed

by optical homodyne tomography [113].

Various nonclassical, non-Gaussian optical quantum states with negative values

of W(x, p ) h ave been generated. Those states can be categorized into two fam-

ilies. One family is the Fock states and their variants combined with coherent

states [312, 316–319], created in a non-collinear PDC conﬁguration of the signal

and idler photons. The other is the photon-subtracted squeezed states, where a

small fraction of a squeezed vacuum beam is beam-split and guided into a photon

counter as trigger photons, and the remaining beam is conditioned by the detection

of the trigger photons [315]. In the ideal case, a squeezed vacuum is a superposi-

tion of even photon-number states where the signal and idler photons are collinear,

thus, one-photon-subtracted squeezed states must be a particular superposition of

odd photon-number states. These states are close to optical Schrödinger-cat states

with small coherent amplitudes, and thereby referred to as optical “Schrödinger kit-

tens” [186, 320].

In the previous works of Schrödinger kittens, potassium niobate (KNbO

)

crystals are used as nonlinear optical media for an optical parametric ampl iﬁ-

er (OPA) [320], or in an optical parametric oscillator (OPO) far below thresh-

old [186]. In the case of experiments with KNbO

, however, it is known that there

is a big source of loss referred to as pump (blue) light induced infrared absorption

(BLIIRA) [321]. The big loss caused by BLIIRA weakens the even-photon nature

of a squeezed vacuum, that is, it weakens entanglement between two modes into

which the squeezed vacuum is beam-split, and yields uncorrelated trigger pho-

tons. They i nduce false clicks in state preparation and consequently degrade the

output conditioned states. The most negative value observed with KNbO

thus far

is 0.026 without any corrections of experimental imperfections [320].

On the other hand, periodically-poled KTiOPO

(PPKTP) has turned out not

to have the BLIIRA effect in continuous-wave squeezing experiments [283, 322].

Therefore, a squeezing level at 860 nm has been signiﬁcantly improved [283].

Thanks to its almost BLIIRA-free property, one can obtain squeezing with high-

er purity (even-photon nature) than that in the case of using KNbO

.Purityof

squeezing depends on how big the portion of a squeezed vacuum can escape from

an OPO cavity. The cavity escape efﬁciency, which can be calculated by a trans-

mittance of an OPO output coupler and all intracavity losses [323] is 97% with

PPKTP, while that of KNbO

is 80% at most.

Let us now explain the generation of a wide range of photon-subtracted squeezed

states, including the single-photon state and a Schrödinger kitten state with very

deep negative dips of the Wigner functions [313]. A single-photon state can be

realized to subtract one photon from a squeezed vacuum with a weakly pumped

OPO [184], but it could not be created in photon-subtraction experiments with

KNbO

. This is because the squeezed states from KNbO

are too impure. In con-

trast, the usage of PPKTP results in low pump-induced losses and hence high

squeezing at high purity. This enables one to generate various states from single-

photon to Schrödinger kitten states by simply tuning the squeezing level which can

be directly controlled by the pump power for the squeezer.

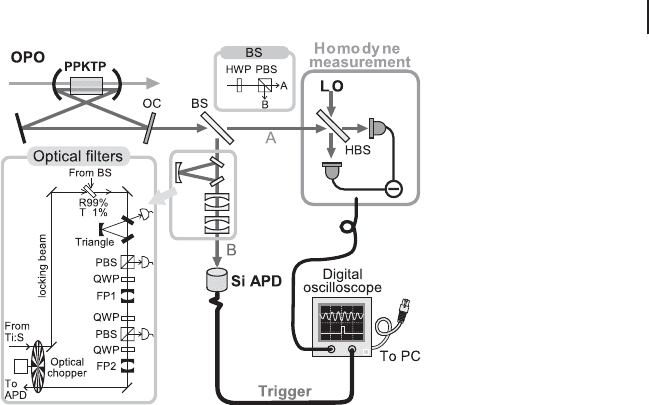
8.2 Experiment: Creation of Non-Gaussian States, Cat States 305

Figure 8.3 Schematic of experimental set-

up [313]. OC: output coupler, HWP: half-wave

plate, PBS: polarizing beam splitter, BS: beam

splitter (consisting of HWP and PBS, variable

splitting ratio), Triangle: triangle cavity, QWP:

quarter-wave plate, FP1 & FP2: Fabry–Perot

cavities, HBS: 50:50 beam-splitter.

A schematic of the experimental setup is shown in Figure 8.3. A continuous-

wave Ti:sapphire laser (Coherent MBR-110) is used as a primary source of the fun-

damental beam at 860 nm, which is mainly used to generate a second harmonic

(430 nm) of about 200 mW by a frequency doubler (a bow-tie cavity with KNbO

). It

is also used as a local oscillator (LO) for homodyne detection, and as probe beams

for various control purposes. The second harmonic beam is used to pump the OPO

with a 10 mm long PPKTP crystal (Raicol Crystals) as a nonlinear medium in an

optical cavity (a bow-tie conﬁguration with a round-trip length of about 523 mm).

The output coupler (OC) of this squeezer cavity has a transmittance of 10.3%. The

intracavity loss is about 0.20.3%, which is nearly independent from the pump

power and much better than that with KNbO

in our case (23%). The FWHM of

the cavity is about 9.3 MHz.

A small fraction (5%) of the squeezed vacuum beam in path A is split at a

beam splitter (BS), guided into a commercial Si-APD (Perkin Elmer SPCM-AQR-

16) through three optical ﬁltering cavities in path B, and is used as trigger signals

for conditional photon subtraction. The ﬁnesses of the ﬁltering cavities are about

60 (Triangle), 600 (FP1), and 1500 (FP2), respectively. All the ﬁltering cavities have

510 times wider bandwidths than that of the OPO. The spectrum of the trig-

ger photons through these ﬁlters consists of a single peak around 860 nm at the

degenerate mode with a bandwidth of 8.6 MHz (FWHM). Other irrelevant, nonde-

generate, modes from the OPO, peaking at every free spectral range of 573 MHz

apart from the degenerate frequency, are sufﬁciently well suppressed. The total

transfer efﬁciency after the BS for the mode of interest is about 30% just in front

of the Si-APD. The trigger counting rate varies from less than 1 up to 50 kcps,

306 8 Hybrid Quantum Information Processing

changing with the pump power of OPO from 1 up to 160 mW and splitting ratios.

These trigger counting rates are mostly much greater than the Si-APD dark counts

(100 cps).

Reducing background light is crucial for using an Si-APD because bright back-

ground light easily degrades signal-to-noise ratio of trigger photons. Usually, weak

coherent beams are used as references to lock optical cavities [283], but they directly

yield vast amounts of counts. Therefore, one has to contrive ways to count photons

and lock optical cavities in the same experimental setup.

For that purpose, Wakui et al. applied a time sharing control of the system by a

“sample-and-hold locking” technique which enables us to alternatively switch the

system from a “locking time-bin” to a “measurement time-bin” [313]. In the locking

time-bin, the resonant frequencies of the ﬁltering cavities are locked in a conven-

tional manner (FM-sideband locking technique [185]). Servo ampliﬁers keep the

ﬁltering cavities in resonance by piezo actuators via demodulating the modulation

applied to a “locking beam” (F igure 8.3). In the measurement time-bin, the locking

beam is completely blocked for photon counting and servo ampliﬁers hold the sys-

tem in the same state as right before the locking beam is blocked. To perform this

periodically, the locking beam ﬁrst passes through an optical chopper (the chop-

ping frequency is 500 Hz), is guided into the ﬁltering cavities, and then returning

to the same chopper again after passing them through (Figure 8.3). When the lock-

ing beam passes through at one side of the optical chopper, it is blocked at the other

side, and vice versa, and thus one realizes the time sharing control. Wakui et al. al-

so made the servo ampliﬁers accept external timing signals in order to be able to

be synchronized to the optical chopper’s driver. A different experimental approach

other than the method presented here can be found in [186].

The generated nonclassical states of light are combined with the LO at a 50 : 50

beam-splitter (HBS) and detected by a balanced homodyne detector with Si pho-

todiodes (Hamamatsu S3759, anti-reﬂective coated at 860 nm, 99.6% quantum ef-

ﬁciency). In order to improve the homodyne efﬁciency, the LO beam is spatially

ﬁltered by a mode cleaning cavity which yields the same spatial mode as the OPO

output. The propagation loss mainly comes from the pickup of a squeezed vacuum

itself (5% at BS), and the homodyne efﬁciency is 98%.

For every trigger signal from the Si-APD, a digital oscilloscope (LeCroy WaveRun-

ner 6050A) samples homodyne signals around the time when trigger photons are

detected. Recall the discussion in Section 3.2.3.2; the spectroscope and power mea-

surements of the more conventional frequency-domain CV experiments are here in

the time-domain approach replaced by the digital oscilloscope and amplitude mea-

surements. Now, each segment of data contains homodyne signals over a period

0.5 µs [see Eq. (3.82)]. These are piled one after another until 10 000 segments

ﬁll up the oscilloscope’s memory in a single run of the experiment. Each segment

of the homodyne signals are sent to a PC, and then time-integrated after being

multiplied by a particular temporal mode function Ψ

(t). Each Wigner function is

reconstructed using the iterative maximum-likelihood estimation algorithm [302]

from about 50 000 data points of quadrature amplitude.

8.2 Experiment: Creation of Non-Gaussian States, Cat States 307

ThetemporalmodefunctionΨ

(t) should be chosen such that it deﬁnes the

signal mode which shares the maximal entanglement with the trigger photon

mode. The trigger photon mode is well localized in the time domain at least within

T  1 ns. This depends on the single-photon timing resolution of SPCM and is

much shorter than the inverse bandwidth of the squeezed vacua.Thebandwidthof

the squeezed vacua are typically 2B  10 MHz and can be characterized by the

bandwidthoftheOPOcavity.ForsuchasmallBT, a single mode description is

valid [183] (see Figure 2.11). In a good approximation, one can consider Ψ

(t)ina

form [184] Ψ

(t) D

ζ

jtj

, assuming a trigger signal detected at t D 0where

 (γ

C γ

)/2 determines the characteristic bandwidth ζ

/2π  4.6 MHz.

Here, the leakage rate of the output coupler is γ

 57 MHz and the cavity loss

rate is γ

 1.2 MHz.

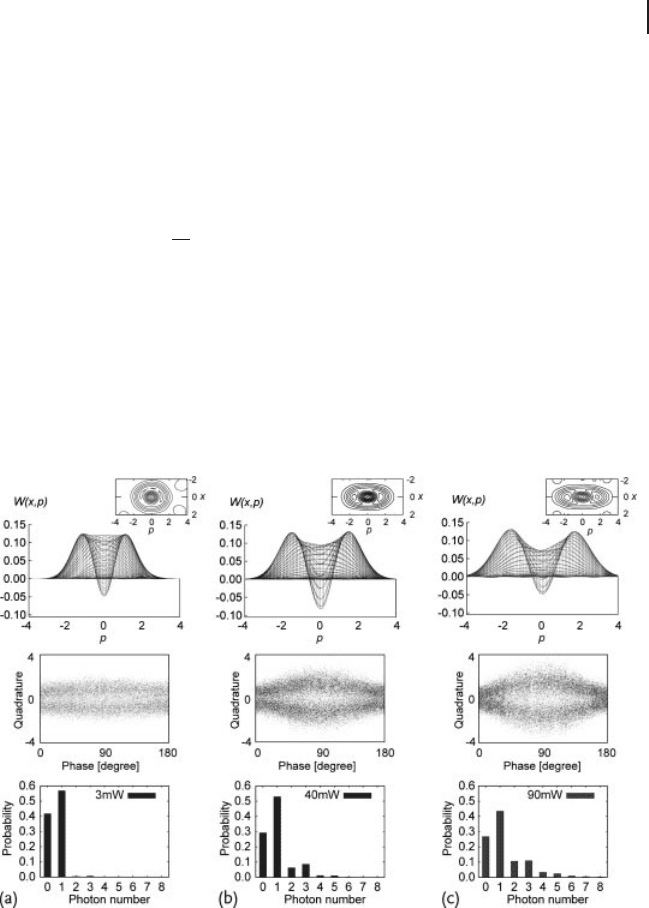
Figure 8.4 shows experimental Wigner functions (top panels) and its contour

plots (insets in top panels), raw data of quadrature distributions over half a pe-

riod (middle panels), and photon-number distributions (bottom panels) of the

photon-subtracted squeezed states. First, experimental density matrices in the

Fock (photon-number state) basis are obtained from the raw data in the middle

Figure 8.4 Experimental Wigner functions

(top panels) constructed from raw data with-

out any correction of measurement imper-

fections in the case of 5% splitting ratio. (a)

The single-photon state generated by 0.7 dB

squeezed input. (b) and (c) Schrödinger kit-

tens generated by 2.6 and 3.7 dB squeezed

inputs, respectively. The values of the Wign-

er function at the origin are (a) W(0, 0) D

0.049, (b) W(0, 0) D0.083, and (c)

W(0, 0) D0.048. The insets in the top

panels are the contours of the Wigner func-

tions. The middle panels are quadrature dis-

tributions obtained by homodyne detection.

The bottom panels are photon-number distri-

butions obtained by the iterative maximum-

likelihood estimation. In the calculations in

this section, units of „D1areused.

308 8 Hybrid Quantum Information Processing

panels by using the iterative maximum-likelihood estimation. Then, the Wigner

functions in the top panels can be directly calculated from the density matrices.

Here, any corrections for measurement imperfections are not applied. The bottom

panels are diagonal elements of the density matrices in the Fock basis.

The negativity of the photon-subtracted squeezed states tightly depends on a

signal-to-noise (S/N) ratio of trigger photons because one cannot distinguish trig-

ger (signal) clicks and false (noise) clicks in state preparation. False clicks just yield

vacuum con tributions to the gen erated states. A vacuum state has a Gaussian dis-

tribution of the Wigner function and a positive peak at its origin. Therefore, the

negative dips of the generated states become shallow when the S/N ratio gets worse

and worse, that is, the vacuum contributions increase more and more.

Figure 8.4a corresponds to a single-photon state generated by 0.7 dB squeezed

input. In such a low level of squeezing, the counting rate of trigger photons is

extremely low (less than 1 kcps) and become comparable to Si-APD’s dark-count

rate (100 cps). Thus, the negativity in the single-photon state easily disappears even

with a small amount of false clicks rather than that in the Schrödinger-kitten states.

Therefore, the single-photon state particularly requires a nearly pure squeezed state

generated with PPKTP, as mentioned above.

Figure 8.4b and c are for Schrödinger kittens with two kinds of amplitudes gener-

ated by 2.6 and 3.7 dB squeezed inputs, respectively. The odd-number enhanced

distributions of photon numbers are illust rated in the bottom panels. Furthermore,

these two states can be seen as superpositions of mesoscopically distinct compo-

nents. The large negativity is obtained in a wide range of squeezing levels.

The experimental values of the Wigner functions at their origins are Fig-

ure 8.4a: W(0, 0) D0.049, Figure 8.4b: W(0, 0) D0.083, and Figure 8.4c:

W(0, 0) D0.048.

These values are signiﬁcantly improved, compared to the

values with KNbO

By using a similar technology, Neergaard-Nielsen et al. succeeded in creating a

single photon state [324], which ﬁts CV experiments.

Figure 8.5 shows the setup for creation of a single photon state for CV QIP [324].

This setup is very similar to Figure 8.3, except for frequency shifts to ω

and ω



from the fundamental frequency ω

of the laser where jω

 ω

j corresponds to

the free spectral range (FSR) of the OPO cavity. Since the ﬁl tering cavities are all

resonant with ω



,theω



component of the output of the OPO passes through

the cavities and hits a single-photon detector (APD: avalanche photodiode). On the

other hand, the ω

component is reﬂected and goes to a homodyne measurement

setup. Here, ω

and ω



components have EPR-type entanglement.

When there is a click at the APD, a single photon state appears at frequency ω

which is detected by using the local oscillator of frequency ω

of the homodyne

measurement. Note that the difference between the previously described single-

photon subtraction scheme and the scheme introduced in the preceding paragraph

is that single-photon subtraction uses the ω

component which has even-photon

2) Note that here, in order to compute the measured negativities, the convention „D1wasused,

differing from our usual convention of „D1/2 throughout this book.

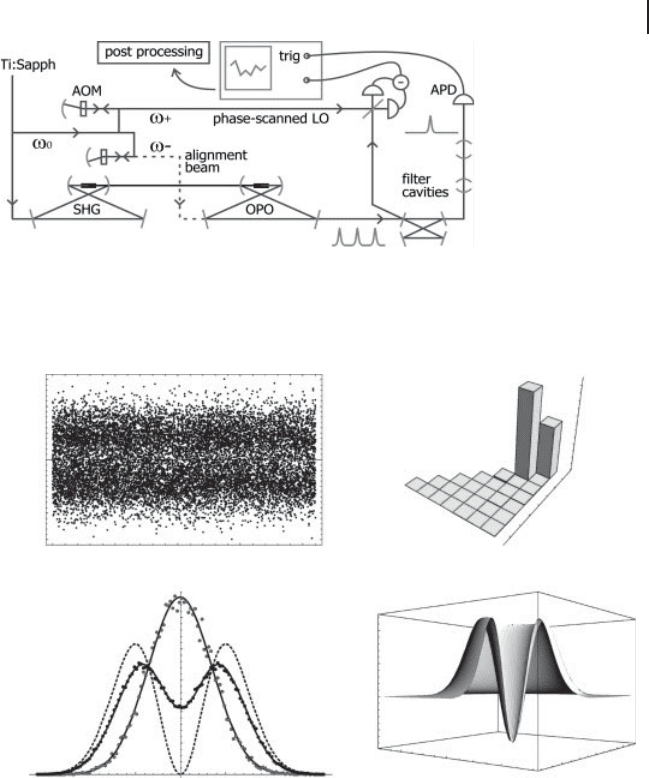
8.2 Experiment: Creation of Non-Gaussian States, Cat States 309

Figure 8.5 Experimental setup for single-

photon creation for CV QIP demonstrated by

Neergaard-Nielsen et al. [324]. SHG: second

harmonic generator for pumping the OPO,

AOM: acousto optic modulator to shift the

fundamental frequency ω

, LO: local oscilla-

tor, APD: avalanche photo diode.

–3

0.5

0.4

0.3

0.2

0.1

–2

–1

Quadrature value

1–1–2–3 2 3

–2

–0.05

0.05

0.1

LO phase (rad)

0.2

0.4

0.6

(a) (c)

(b) (d)

Figure 8.6 Experimental results for single-

photon creation for CV QIP demonstrated by

Neergaard-Nielsen et al. [324]. (a) Part of the

recorded quadrature data set with correspond-

ing phases. (b) Histogram of distribution of

conditional quadrature points and vacuum

points. The dashed curve is the ideal single

photon distribution. (c) The density matrix of

the state reconstructed via the maximum like-

lihood method. (d) The corresponding Wigner

function.

nature and not EPR-type entanglement. Figure 8.6 shows the experimental re-

sults [324].