Fujita S., Ito K., Godoy S. Quantum Theory of Conducting Matter

Подождите немного. Документ загружается.

References 191

3. I. Terasaki, M. Hase, A. Maeda, K. Uchinokura, T. Kimura, K. Kishio, I. Tanaka and H. Kojima,

Physica C 193, 365 (1992).

4. W. Pauli, Zeits. f. Phys. 41, 81 (1927).

5. e.g. L. D. Landau and E. M. Lifshitz, Statistical Physics, part I, 3rd ed. (Pergamon Press, Ox-

ford, England, 1980), pp. 171–174.

6. S. Fujita, T. Obata, T. F. Shane and D. L. Morabito, Phys. Rev. B 63, 54402 (2001).

7. L. Onsager, Phil. Mag. 43, 1006 (1952).

Chapter 15

d-Wave Cooper Pair

The d-wave Cooper pairs (pairons) in cuprates with strong binding along the a- and

b-axes are shown to arise from the optical-phonon exchange attraction.

15.1 Introduction

Josephson tunneling experiments in underdoped cuprates [1,2] indicate that Cooper

pairs (pairons) in cuprates are of a d-wave type with a strong binding occurring in

the a- and b-crystal axes, see Fig. 15.1. Such lattice-dependent anisotropy may be

explained by an intrinsically anisotropic optical-phonon-exchange and Fermi sur-

face, rather than any spin-dependent mechanisms.

15.2 Phonon–Exchange Attraction

The electron-pair density matrix ρ(k

, k

; k

, k

, t) ≡ ρ(1, 2, 3, 4, t), in the pres-

ence of a Coulomb interaction v

, changes in time following a quantum Liouville

equation

i

⭸ρ(1, 2; 3, 4, t)

⭸t



[

1, 2|v

|5, 6ρ(5, 6; 3, 4, t)

−5, 6|v

|3, 4ρ(1, 2; 5, 6, t)

]

. (15.1)

1, 2|v

|3, 4≡4πe

−k

, k

≡

4π

Earlier in Section 2.3 we showed that if a phonon having momentum q and

energy ω

is exchanged, the density matrix ρ changes following the same equation

with an effective interaction v



1, 2 |v

|3, 4



=|V

ω

(

−

)

−(ω

)

−k

, (15.2)

S. Fujita et al., Quantum Theory of Conducting Matter,

DOI 10.1007/978-0-387-88211-6

15,



Springer Science+Business Media, LLC 2009

193

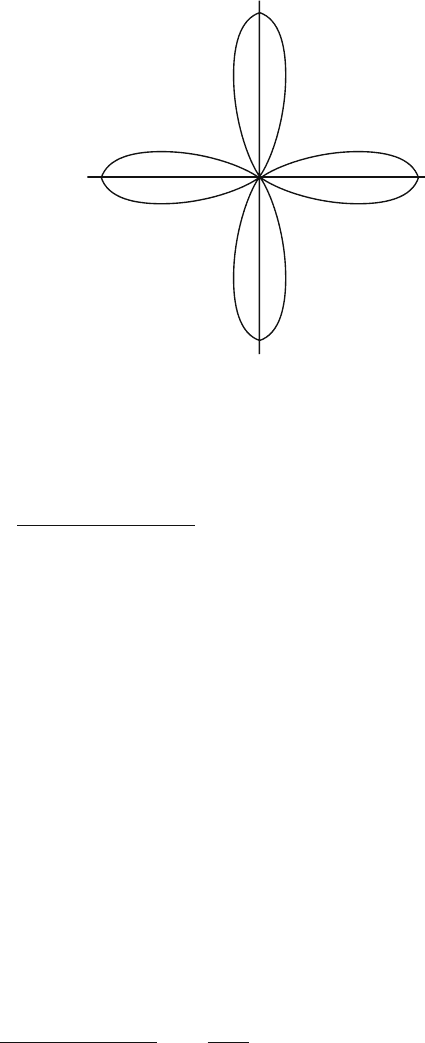
194 15 d-Wave Cooper Pair

Fig. 15.1 A d-wave Cooper

pair with strong binding

along the a-andb-axes

[010]

[100]

where 

≡ 

is the electron energy, and V

the electron–phonon interaction

strength. We note that this result (15.2) is partially in agreement with the form of a

pairing Hamiltonian appearing in Equation (2.4) of the original BCS work [3]:

int



k,σ





,σ





ω

(

−

k+q

)

−(ω

)

†



+qσ



†

k+qσ

kσ



. (15.3)

We examine the effect of the exchange of the phonon with momentum q and

energy ω

on ρ. The most important attraction occurs in the speciﬁc k-space region

near the Fermi surface where the phonon-mediated momentum transfer q is nearly

parallel to the surface so that 

− 

= 0. As we see in this example, the phonon–

exchange attraction is direction-dependent. This is important for the d-wave pairon

formation discussed below.

The nature of phonon-exchange interaction v

depends on the type of phonons.

Consider ﬁrst longitudinal acoustic phonons, whose dispersion relation is linear:

ω

= c

q . (c

= sound speed) (15.4)

If a deformation potential model [4] is assumed, the interaction strength V

= A(/2ω

)

(1/2)

iq . (A = constant) (15.5)

Using Equations (15.4) and (15.5), we obtain

ω

(

−

)

−(ω

)

∼−



≡−v

(15.6)

15.3 d-Wave Pairon Formalism 195

for the dominant attraction at 0 K (

− 

= 0), showing that phonons of any

wavelengths are equally effective. For optical phonons whose dispersion relation is

given by

ω

= 

(constant) , (15.7)

we obtain

ω

(

−

)

−(ω

)

∼−



, (15.8)

indicating that optical phonons of shorter wavelengths (greater q) are more effective.

The wavelength λ ≡ 2π/q of a phonon has a lower bound 2a

, a

= the lattice

constant, yielding a shorter interaction range compared with the case of an acoustic

phonon exchange. The ratio of the rhs of Equations (15.8) and (15.6), c

/

,isof

the order unity for the maximum q

max

= π/a

. Hence the short-wavelength optical

phonon exchange is as effective as the acoustic phonon exchange. The optical-

phonon exchange pairing becomes weaker for longer wavelengths (small q).

15.3 d-Wave Pairon Formalism

Let us consider the copper plane. Linear arrays of O-O and Cu-O-Cu alternate in

the [100] and [010] directions, see Fig. 13.2 (a). Thus we recognize longitudinal

optical modes of oscillations along the a- and b-axes. Now let us look at the motion

of an “electron” wave packet extending over unit cells. If the “electron” density is

small, the Fermi surface should be a small circle as shown in the central part in

Fig. 13.3 (a). Next consider a “hole” wave packet. If the “hole” density is small, the

Fermi surface should consist of four small pockets near the Brillouin zone corners as

shown in Fig. 13.3 (b). Under the assumption of such a Fermi surface, pair creation

of ± pairons by means of an optical phonon exchange can occur as shown in the

ﬁgure. Here a single-phonon exchange generates the electron transition from A in

the O-Fermi sheet to B in the Cu-Fermi sheet and the electron transition from A



, creating the − pairon at (B, B



) and the + pairon at (A, A



). The optical phonon

having momentum q nearly parallel to the a-axis is exchanged here. Likewise, the

optical phonon with a momentum nearly along the b-axis helps create ± pairons.

But because of the location of the Fermi surface, there is no pairon formation in

the direction [110] and [1

10]. Consequently the pairon is of a d-wave type with the

dominant attraction along the a- and b-axes, see Fig. 15.1.

If the doping is increased, the O-Fermi surface grows as shown in Fig. 13.4 (b),

At the end of the overdoping, the O-Fermi surface undergoes a curvature inversion

as in Fig. 13.4 (c) and (d). Near the inﬂection point, the pairon is isotropic and

s-wave type.

196 15 d-Wave Cooper Pair

A direct way of mapping a 2D Fermi surface is to perform an angle-resolved

photo-emission spectroscopy (ARPES) [5, 6]. It would be highly desirable to see

the curvature inversion by this technique.

15.4 Discussion

The attraction generated by the optical-phonon exchange is intrinsically anisotropic.

Because of the location of the Fermi surface in the optimum and underdoped cuprate

the exchange of an optical longitudinal phonon generates a d-wave Cooper pair with

the dominant attraction in the directions [110] and [1

10]. Our model predicts that the

d-wave character will be lost in the extremely overdoped sample, which is observed

in the experiments.

References

1. D. A. Wollman, et al., Phys. Rev. Lett. 71, 2134 (1993).

2. C. C. Tsuei, et al., Nature 386, 481 (1997).

3. J. Bardeen, L. N. Cooper and J. R. Schrieffer, Phys. Rev. 108, 1175 (1957).

4. W. A. Harrison, Solid State Theory (Dover, New York, 1980) pp. 390–397.

5. D. S. Dessau, et al., Phys. Rev. Lett. 71, 2781 (1993).

6. Z.-X. Shen, et al., Phys. Rev. Lett. 70, 1553 (1993).

Chapter 16

Transport Properties Above T

Magnetotransport properties in Nd

2−x

CuO

, and La

2−x

CuO

above T

show

unusual behaviors with respect to the temperature (T )-and doping concentration

(x)-dependence. The resistivity ρ in optimum (highest T

) samples shows a T -linear

behavior while that in highly overdoped samples exhibits a T -quadratic behavior.

The cot θ

, where θ

is the Hall angle, shows a T -quadratic behavior. The Hall

coefﬁcient R

changes the sign as the concentration x passes the super-to-normal

phase. We shall explain these properties based on the independent pairon model in

which ± pairons and conduction electrons are carriers in the superconductor.

16.1 Introduction

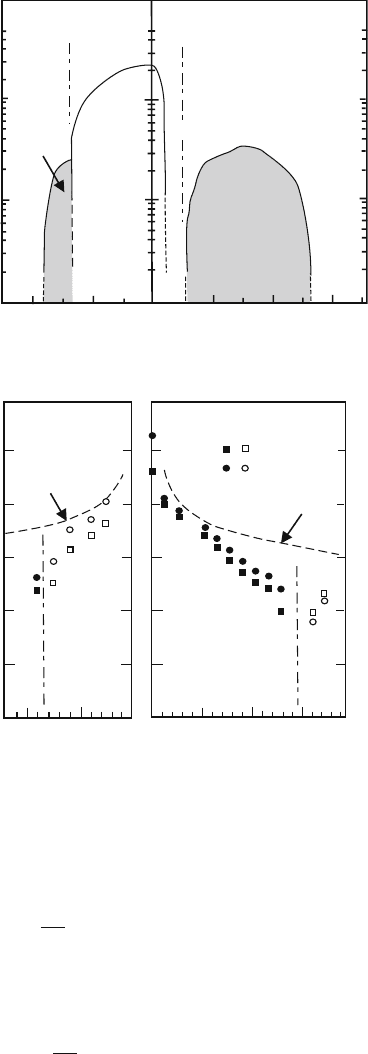
A summary of data for the resistivity ρ in various cuprates at optimum doping after

Iye [1] is shown as solid lines in Fig. 16.1. The T -linear behavior:

ρ ∝ T (16.1)

has been observed ever since the discovery of the ﬁrst HTSC by Bednorz and M

uller

[2]. Data for ρ in highly overdoped samples are shown in dotted lines; they show a

T -quadratic behavior. The cot θ

, where θ

is the Hall angle, follows a T -quadratic

behavior

cot θ

∝ T

. (16.2)

Data for the Hall coefﬁcient R

in Nd

2−x

CuO

, and La

2−x

CuO

versus

the “electron” (“hole”) - concentration are shown in Fig. 16.2 (b) [3–6]. Note that

the sign changes in R

at the end of the overdoping region (dash-dot lines). Also

note that the magnitude of the Hall coefﬁcient |R

| is smaller for higher T and

for greater x in superconductor samples. These data clearly indicate that at least

two (charge) carriers contribute to the electrical conduction. We shall show that

S. Fujita et al., Quantum Theory of Conducting Matter,

DOI 10.1007/978-0-387-88211-6

16,



Springer Science+Business Media, LLC 2009

197

198 16 Transport Properties Above T

Fig. 16.1 Resistivity in the

ab plane, ρ

versus

temperature T . Solid lines

represent data for cuprates at

optimum doping and dashed

lines data for highly

overdoped samples, after

Iye [1]

the unusual magnetotransport properties can quantitatively be explained based on a

two-carrier model, in which fermionic electrons and bosonic pairons are scattered

by phonons.

16.2 Simple Kinetic Theory

16.2.1 Resistivity

We use simple kinetic theory to describe the transport properties [7]. Kinetic theory

originally was developed for a dilute gas. Since a conductor is far from being the

gas, we shall discuss the applicability of kinetic theory. The Bloch wave packet in a

crystal lattice extends over one unit cell or more, and the lattice-ion force averaged

over a unit cell vanishes, see Book 1, Equation (10.12). Hence the conduction elec-

tron (“electron,” “hole”) runs straight and changes direction if it hits an impurity or

phonon (wave packet). The electron–electron collision conserves the net momen-

tum, and hence, its contribution to the conductivity is zero. Upon the application of

a magnetic ﬁeld, the system develops a Hall electric ﬁeld so as to balance out the

Lorentz magnetic force on the average, see Fig. 16.3. Thus, the electron still moves

straight and is scattered by impurities and phonons, which makes the kinetic theory

applicable.

Consider a system of “holes,” each having effective mass m

and charge +e,

scattered by phonons. Assume a weak electric ﬁeld E applied along the x-axis.

Newton’s equation of motion for the “hole” with the neglect of the scattering is

16.2 Simple Kinetic Theory 199

Fig. 16.2 (a) Phase diagrams

for Nd

2−x

Cuo

,and

2−x

CuO

.(b) Doping

dependence of Hall

coefﬁcient R

,after

Takagi [3]

(a)

Super C

Metallic Metallic

Super C

x (Ce) x (Sr)

| [cm

/C]

0.2 0.1 0 0.1 0.2 0.3

500

100

2-x

CuO

4-δ

2-x

CuO

(b)

x (Ce) x (Sr)

< 0R

< 0

| [cm

/C]

0.2 0.1

0 0.1 0.2 0.3

–2

–4

–6

1/x

2-x

CuO

2-x

CuO

at 300 K

at 80 K

1/x

/dt = eE. Solving it for v

and assuming that the acceleration persists in the

mean free time τ

, we obtain

(16.3)

for the drift velocity υ

. The current density (x-component) j is

j = en

E, (16.4)

200 16 Transport Properties Above T

Fig. 16.3 (a) The magnetic

and electric forces (F

, F

)

balance out to zero in the Hall

effect measurement. (b)The

Hall angle θ

(a)

(b)

where n

is the “hole” density. Assuming Ohm’s law: j = σ E, we obtain an ex-

pression for the electrical conductivity:

, (16.5)

where γ

≡ τ

−1

is the scattering rate. This rate can be computed, using

= n

(16.6)

where S

is the scattering diameter. If acoustic phonons having average energies:

ω

≡α

ω

 k

T,α

∼ 0.20 are assumed, the phonon number density is [8]

= n

[exp(α

ω

T ) −1]

−1

 n

ω

, (16.7)

where n

≡ (2π)

−2

(

k is the small k-space area where the acoustic phonons are

located.

Using Equations (16.5), (16.6), and (16.7), we obtain

, a ≡

ω

. (16.8)

Thus, the resistivity ρ (conductivity σ ) is (inversely) proportional to T .

Let us now consider a system of +pairons, each having charge +2e and mov-

ing with the linear dispersion relation:  = cp. Since v

= (d/dp)(⭸ p/⭸ p

)

= c(p

/p), Newton’s equation of motion is



= 2eE, (16.9)

16.2 Simple Kinetic Theory 201

yielding v

= 2e(c

/)Et + initial velocity. After averaging over the angles, we

obtain

(2)

= 2ec

E 

−1

, (16.10)

where τ

is the pairon mean free time and the angular brackets denote a thermal

average. Using this and Ohm’s law, we obtain

= (2e)

c

−1

n

−1

,γ

≡ γ

−1

, (16.11)

where n

is the pairon density. If we assume a Boltzmann distribution for bosonic

pairons above T

,(T > T

), we obtain



−1

≡

2π

(2π)



∞

dp p



Bcp

2π

(2π)



∞

dp pe

Bep

= (k

T )

−1

. (16.12)

The rate γ

is calculated with the assumption of a phonon scattering. We then

obtain

, b ≡

ω

. (16.13)

The total conductivity σ is σ

+σ

. Taking the inverse of σ, we obtain

ρ ≡

(an

T +2bn

)

. (16.14)

16.2.2 Hall Coefﬁcient

We take a rectangular sample having only “holes,” see Fig. 16.3 (a). The current j

runs in the z-direction. Experiments show that if a magnetic ﬁeld B is applied in the

y-direction, the sample develops a Hall electric ﬁeld E

so that the magnetic force

≡ e(v

×B) be balanced out to zero:

e(E

×B) = 0orE

=−v

B. (16.15)

If the sample contains +pairons only, Equation (16.15) also holds. Since the

“hole” and the + pairon have like charges (e, 2e) the two components (“holes,”

+pairons) separately maintain drift velocities (v

(1)

(2)

) and Hall ﬁelds (E

(1)

, E

(2)

)

so that

( j)

=−v

( j)

B, j = 1, 2. (16.16)

Fujita S., Ito K., Godoy S. Quantum Theory of Conducting Matter - Superconductivity

Подождите немного. Документ загружается.