Fujita S., Ito K., Godoy S. Quantum Theory of Conducting Matter

Подождите немного. Документ загружается.

Chapter 14

The Susceptibility in Cuprates

The unusual concentration (x) and temperature (T ) dependence of the suscep-

tibility χ in La

2−x

CuO

is discussed in this chapter. The susceptibility χ at

400 K increases with x in the range 0.04 < x < 0.25 and decreases in the range

0.25 < x < 0.33. The maximum at x = 0.25 is interpreted in terms of the curvature

inversion of the O Fermi surface. At the inﬂection point the density of states is

extremely high, which causes χ to have a temperature behavior χ = A

+ B

, B

= constant). The Cooper pair (pairon) has no net spin, and hence its spin

contribution to χ is zero. But its motion contributes diamagnetically. This gener-

ates a T -dependent contribution −B

/T (B

= constant). These two contributions

generate a χ maximum at T

in the range 0.15 < x < 0.25.

14.1 Introduction

Takagi et al. [1], Torrance et al. [2], Terasaki et al. [3], and others studied transport

and magnetic properties of La

2−x

CuO

over a wide range of concentration x

including a nonsuperconducting phase beyond the overdoped region. Remarkable

changes, in the resistivity ρ, the Hall coefﬁcient R

and the magnetic susceptibility

χ were observed near the super-to-normal transition at x = 0.25. The susceptibility

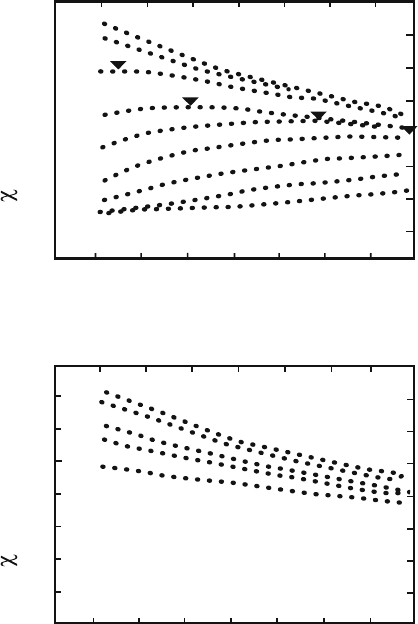
data after Torrance et al. [2] are reproduced in Fig. 14.1. The notable features of the

data are as follows:

(a) χ at x = 0.04 is nearly ﬂat for 40K < T < 400 K. At this concentration the

material is not a superconductor.

(b) The susceptibility χ at 400 K grows with increasing x in the range 0.04 <

x < 0.25 and decreases in the range 0.25 < x. The turning point x =

0.25 roughly corresponds to the concentration at which the superconducting

temperature T

vanishes. See Fig. 14.2 (a).

and χ has a T -dependence represented by

χ = A

+ B

/T, A

, B

= (positive) constants. (14.1)

S. Fujita et al., Quantum Theory of Conducting Matter,

DOI 10.1007/978-0-387-88211-6

14,



Springer Science+Business Media, LLC 2009

181

182 14 The Susceptibility in Cuprates

(d) In the range 0.06 < x < 0.15, χ has the following T dependence:

χ = A

− B

/T, A

, B

= constants. (14.2)

The end point x = 0.15 coincides with the highest T

, see Figs. 14.1 (a) and

14.2 (a).

(e) In the range 0.15 < x < 0.25, χ has a maximum, indicated by solid triangles

 in Fig. 14.1 (a), at T

.ThisT

disappears at x = 0.25, where T

vanishes,

see Fig. 14.1 (a).

The parent material La

CuO

is a cuprate of a perovskite structure. It is an anti-

ferromagnetic insulator with the N

eel temperature T

= 230 K. The substitution of

trivalent La by divalent Sr reduces the number of electrons and changes the ionicity

of the group (LaO) neighboring the copper plane (CuO

). This in turn reduces the

Fig. 14.1 Normal-state

susceptibility of

2−x

CuO

,for

increasing x,(a) increases for

0.04 < x < 0.25 and (b)

decreases for

0.25 < x < 0.33, after

Torrance et al. [2]. The solid

triangles mark the

temperatures where χ is a

maximum

2-x

CuO

2-x

CuO

Temperature (K)

100 200 300

400

1.0

2.0

100 200 300

400

(b)

(a)

0.04

0.25

0.23

0.21

0.19

0.17

0.15

0.12

0.08

0.25

0.27

0.29

0.31

0.33

(10

–4

emu/mol)

1.0

2.0

(10

–4

emu/mol)

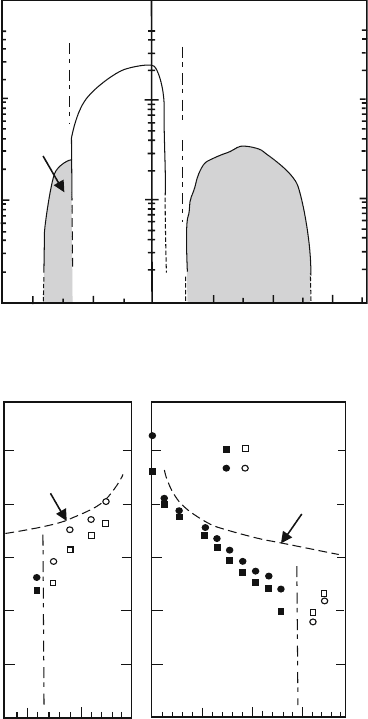
14.1 Introduction 183

Fig. 14.2 (a) Critical

temperature T

concentration x for

2−x

CuO

and

2−x

CuO

4−δ

.(b)Hall

coefﬁcient (absolute value)

| vs x, after Takagi

et al. [1]

(a)

Super C

Metallic Metallic

Super C

x (Ce) x (Sr)

| [cm

/C]

0.2 0.1 0 0.1 0.2 0.3

500

100

2-x

CuO

4-δ

2-x

CuO

(b)

x (Ce) x (Sr)

< 0R

< 0

| [cm

/C]

0.2 0.1

0 0.1 0.2 0.3

–2

–4

–6

1/x

2-x

CuO

2-x

CuO

at 300 K

at 80 K

1/x

number of electrons in the O sublattice of the copper plane due to the perovskite

structure. Thus, the doping generates “holes” in the O Fermi surface, which can be

seen by the positive R

, see Fig. 14.2 (b), after Takagi et al. [1], where (a) phase

diagram and (b) the doping concentration (x) dependence of R

are shown. The

conduction electrons (“holes,” “electrons”) in the copper plane can contribute to

the magnetization by their spins and motion. According to the elementary theories

by Pauli [4] and by Landau [5], the susceptibility χ due to the electrons of high

degeneracy:

T  T

(Fermi temperature) (14.3)

184 14 The Susceptibility in Cuprates

is T -independent. This explains the feature (a). The rest of the features (b) through

(e) must be explained by introducing new mechanisms and/or new charge-spin

carriers.

14.2 Theory

A. The feature (a) suggests a Pauli paramagnetism:

χ =

2μ

N(

),μ

= Bohr magneton, (14.4)

where N() is the density of states per spin, and A the sample area. Note that this χ

is T -independent. If we use an effective mass (m

∗

) approximation (quasifree elec-

tron model):

 =

∗

+ p

), (14.5)

the density of states per spin in 2D is

N() = m

∗

A(π 

)

−1

, (14.6)

which is independent of energy .

B. At high temperatures 400 K, the Pauli paramagnetism and the Landau diamag-

netism can account for the behavior (b) as follows.

The doping in La

2−x

CuO

reduces the number of electrons in the O Fermi

sheet without changing the Cu Fermi surface at the center of the Brillouin zone, see

Fig. 14.3 (a), (b), (c), and (d). A further doping changes the nature of the O Fermi

surface from “hole-like” in (c) to “electron-like” in (d). Observe the curvature sign

change. The density of states, N, has a maximum at the point of the curvature inver-

sion (x = 0.25). In this neighborhood χ is T -dependent, which will be explained in

the next subsection [6].

C. In the region 0.25 < x < 0.33 the Hall coefﬁcient R

is negative, see

Fig. 14.2 (b), indicating that the “electron” is the majority carrier in the conduction.

Assume that the density of states per spin at zero magnetic ﬁeld is given by

N() = N

δ( −

), c

,

= constants. (14.7)

The density of states in an ideal 2D system is energy-independent,

see Equation (14.7), and this part is represented by N

. By examining the changes

 = 

, and it is symmetric in the neighborhood of this point. We represented this

component by the delta-function term c

δ( −

), see Fig. 14.4.

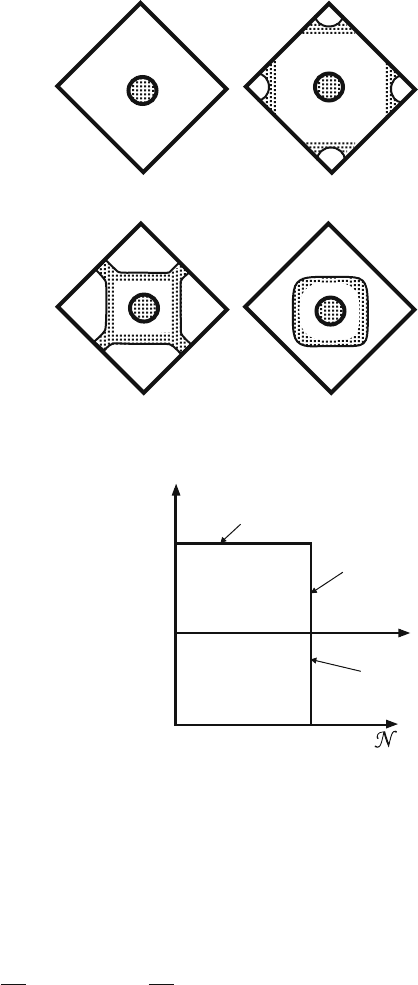
14.2 Theory 185

Fig. 14.3 The O Fermi

surface changes “hole”-like

in (c) to “electron”-like in (d)

as the number of electrons is

reduced

(a)

(b)

(c)

(d)

Fig. 14.4 The density of

states per spin N() at zero

magnetic ﬁeld

top of the band

density of states

2D "holes"

2D "electrons"

(ε−ε

)

(ε)

When a magnetic ﬁeld is applied, the electron energy is split, and the up-spin (+)

and down-spin (−) electrons have different energies:



= 

∓μ

B = 

∓ x, x ≡ μ

B . (14.8)

The magnetization (magnetic moment per area) I is given by

I =

− N

−

) ≡

⌬N , (14.9)

where N

−

) is the number of up- (down-) spin electrons. The electron-number

difference ⌬N = N

− N

−

can be read from Fig. 14.5, and is given by

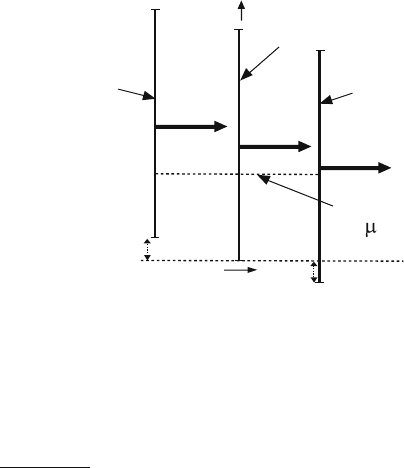
186 14 The Susceptibility in Cuprates

Fig. 14.5 The spin-dependent

density of states N

in the

presence of a magnetic ﬁeld

energy

– spin

+ spin

chemical

potential

density of states

no field

⌬N =





−x

(

) f (

; μ)d

−





−

(

−

) f (

−

; μ)d

−

, (14.10)

where f is the Fermi distribution function

f (; μ) =

β(−μ)

,β≡ (k

T )

−1

, (14.11)

and 

is the upper band edge, see Fig. 14.4. The spin-dependent densities of states

can be related to that density of the zero-ﬁeld system, N(), by

(

) = N(

+ x),

> −x , (14.12)

−

(

−

) = N(

−

− x),

−

> x , (14.13)

see Fig. 14.5. The two systems of the up-spin and the down-spin electrons are in

equilibrium, and hence they have the same chemical potential, (the dotted level in

Fig. 14.5).

Using Equations (14.11), (14.12), and (14.13) and changing the integration vari-

ables, we obtain from Equation (14.10)

⌬N =





N()[ f ( − x; μ) − f ( + x; μ)]d. (14.14)

The chemical potential μ entering in f must be determined from the normaliza-

tion condition

N = N

+ N

−





N()[ f ( − x; μ) + f ( + x; μ)]d, (14.15)

from which we clearly see that μ is an even function of x. In the present model a

constant density of states N

is assumed, so that μ = 

14.2 Theory 187

We now use N() in Equation (14.7) and evaluate Equation (14.14). The con-

stant term N

reproduces Pauli’s term in Equation (14.4). The delta-function term

generates, to the linear in B,

(⌬N)

= c

cosh

[(

−

)/(2k

T )]

. (14.16)

Multiplying this expression by μ

−1

we obtain the magnetization I. The sus-

ceptibility χ, deﬁned by I = χ B, is given by

T cosh

[(

−

)/(2k

T )]

. (14.17)

This result indicates that (a) if the Fermi energy 

is equal to 

, then χ

behaves

as B

/T and (b) if 

is greater or less than 

, this contribution becomes smaller

because of {cosh

[(

− 

/(2k

T )]}

−1

. Both behaviors are in good qualitative

agreement with the experimental data, see Fig. 14.1.

D. The Cooper pair has zero net spin, and hence there is no spin contribution.

Itsmotionintheab plane can contribute diamagnetically to χ . The system of free

pairons moving in 2D with the linear dispersion relation (12.23) undergoes a BEC

transition at

= 1.24 k

−1

1/2

, (14.18)

where n

is the pairon density. Solving Equation (14.18) for n

, we obtain

= (v

)

. (14.19)

From Fig. 14.2 (a), we see then that n

has a maximum at x = 0.15.

Each pairon with charge q in the presence of a static magnetic ﬁeld moves, fol-

lowing the equation of motion

= q(v ×B), v ≡

⭸

⭸p

, c ≡ (2/π)v

. (14.20)

The cyclotron frequency ω



|q|B . (14.21)

The magnitude of the magnetic moment μ for a circulating pairon is

μ = (current) ×(area) =

|q|r

, (14.22)

188 14 The Susceptibility in Cuprates

where r is the cyclotron radius. Note that the magnetic moment μ is proportional to

the charge magnitude |q| and the cyclotron frequency ω

As Landau’s treatment indicates [5], see Book 1, Section 5.3, the motional dia-

magnetism cannot be treated in terms of the classical orbits, but must be treated

quantum mechanically. We take Onsager’s quantum ﬂux view of magnetization [7].

If a magnetic ﬁeld is applied perpendicular to the ab plane, a set of ﬂux quanta

penetrate the plane. A charged particle circulates about the ﬂux lines, and occasion-

ally its guiding center motion is scattered by impurities, phonons,.... The charged

particle motion always reduces the magnetic ﬁeld energy

(

/(2μ

r. That is,

the motion diamagnetically (with a minus sign) contributes to the magnetization I .

We postulate in view of Equation (14.22) that each pairon contributes an amount

proportional to |q|ω

. We then obtain

pairon

=−α



∞

()|q|ω

()F

(; β, μ)d, α= constant , (14.23)

where F

is the Bose distribution function

() =

β(−μ

)

−1

, (14.24)

with μ

being the pairon chemical potential, normalized such that



()F()d = N

. (14.25)

The magnetization I

pairon

is negative irrespective of whether q = 2e or q =−2e.

The density of states for pairons N

()is

() =

A

2π

. (14.26)

Far above T

, the Bose distribution function F

can be approximated by the clas-

sical (Boltzmann) distribution function

() = e

−β(−μ

)

, T  T

, (14.27)

normalized in the form (14.25). Carrying out the -integration in Equation (14.23),

we obtain

pairon

=−n

⌬/T, n

≡ N

/A, ⌬ ≡ αc

−1

, (14.28)

which establishes the second term of the desired formula (14.2), B

= n

⌬.

E. In the region: 0.15 < x < 0.25 there are pairons whose density (n

) decreases

with increasing x. We can express χ, using Equations (14.1), (14.2), and (14.28) as

14.3 Discussion 189

χ = A(x) + B

(x)/T −n

(x)⌬/T. (14.29)

At x = 0.25, n

= 0, and Equation (14.29) is reduced to Equation (14.1). At

x = 0.15, the pairon density is highest and B

(x) is small since |

− 

(x)| is

not small. Then, Equation (14.29) generates a χ-maximum at T

. Experimentally

= 390 K. Between the two extremes, there are χ-maxima at T

. Numerically

= 260, 150, 70, 20, and 0 at x = 0.17, 0.19, 0.21, 0.23, and 0.25.

14.3 Discussion

The susceptibility χ in La

2−x

CuO

above T

exhibits unusual concentration and

temperature dependence. The doping reduces the number of electrons in the cop-

per plane and changes the O Fermi surface. This generates “holes” in the range

0.04 < x < 0.25 and “electrons” in the range 0.25 < x < 0.33. The dividing point

x = 0.25 corresponds to the curvature inversion point of the O Fermi surface, where

the density of states, N, is greatest. Hence, the susceptibility χ has a maximum. At

this inﬂection point the density of states N has a delta-function singularity, yielding

a T -dependent term B

/T for χ. This term decreases in magnitude as the concen-

tration x is distanced from x = 0.25. The pairons, each having charge q = 2e and

moving with the linear dispersion relation  = (2/π)p, can contribute diamagneti-

cally in the (superconductor) range 0.06 < x < 0.25. Based on the model that the

diamagnetic current is proportional to |q| and ω

(cyclotron frequency), we obtain

the term −⌬n

/T for χ, whose magnitude is greatest at x = 0.15. The two effects,

arising from the Fermi surface curvature inversion and the pairon diamagnetic cur-

rents, are signiﬁcant in the range 0.15 < x < 0.25 and generate the χ maximum at

. Thus, all of the unusual behaviors are explained based on the model in which

pairons coexist with the conduction electrons above T

Terasaki et al. [3] measured the susceptibilities (χ

⊥

, χ



), with the ﬁeld B perpen-

dicular to, and parallel to, the c-axis, in La

2−x

CuO

, examining χ more closely

near the optimum doping (x = 0.15), where T

is the highest. Their data for χ

⊥

are

essentially similar to the data shown in Fig. 14.1. They found, see Fig. 14.6, that

⊥

at x = 0.14, 0.15 is smaller than χ

⊥

at x = 0.12. That is, χ

⊥

has a maximum

at x = 0.12 in the range (100 K < T < 200 K), an anomaly which cannot be

explained if the magnetization comes from the conduction electrons only since the

“hole” density smoothly increases with x. This anomaly can be explained simply

in our model. The pairon density n

has a peak at x = 0.15. Hence, the pairon

diamagnetic contribution can make a small anomaly in the smooth increase due to

the “hole” spin.

The susceptibility of a system of moving charge carriers is relatively easy to

treat. Since the susceptibility χ is an equilibrium property, no complicated scat-

tering effects go into the calculation. We only need to know charge, spin (statis-

tics), and mass (dispersion relation) of each carrier and the Fermi surface of the

conduction electrons. Thus, the measurement and analysis of χ gives a clear-cut

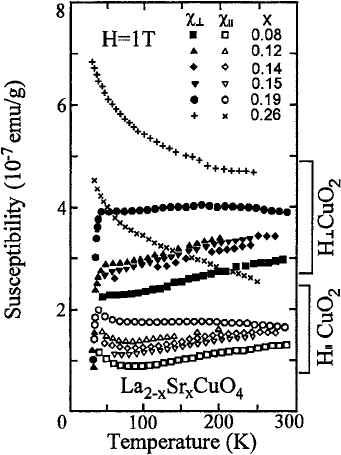
190 14 The Susceptibility in Cuprates

Fig. 14.6 Magnetic

susceptibilities of single

crystal La

2−x

CuO

with

various x under B = 1T,

after Terasaki et al. [3]. For

each χ, χ

⊥

(T, x)and



(T, x) are measured. The

upper curves (or circles)

correspond to χ

⊥

(T, x)with

the ﬁeld perpendicular to the

c-axis, while the lower ones

correspond to χ



(T, x)with

the ﬁeld parallel to the c-axis

information about the charge and spin carriers. The spin paramagnetism, as seen

from Equation (14.13), depends on the density of states N(). Near the inﬂection

point (x = 0.25), the Fermi surface is highly anisotropic. We predict that the sus-

ceptibility χ in La

2−x

CuO

measured with the ﬁeld B

applied at the angle π/4

relative to the a axis should show anisotropy. In our calculation we assumed an

isotropic (angle-averaged) density of states in Equation (14.7). The heat capacity

C, which depends on the density of states should also show a distinct maximum at

x = 0.25.

Consider now Nd

CuO

, which is a cuprate of nonperovskite structure. The sub-

stitution of trivalent Nd by quadrivalent Ce changes the ionicity of the group (NdO)

neighboring the copper plane, which in turn increases the number of electrons in the

Cu sublattice. Thus, the doping in Nd

2−x

CuO

4−δ

generates “electrons” in the

Cu-Fermi sheet, which can be seen by the negative R

, see Fig. 14.2 (b). A further

doping eventually changes the Cu Fermi surface from “electron”-like to “hole”-like.

This change occurs at x = 0.18, see Fig. 14.2 (b), which roughly corresponds to the

vanishing T

, see Fig. 14.2 (a). This is due to the curvature inversion of the Cu Fermi

surface. We predict that the susceptibility χ has a maximum at x = 0.18, and has

the temperature behavior χ = A

+ B

/T .

References

1. H. Takagi, T. Ido, S. Ishibashi, M. Uota, S. Uchida and Y. Tokura, Phys. Rev. B 40, 2254 (1989).

2. J. B. Torrance, A. Bezinge, A. I. Nazzal, T. C. Huang, S. S. P. Parkin, D. T. Keane, S. J. La

Placa, P. M. Horn and G. A. Held, Phys. Rev. B 40, 8872 (1989).

Fujita S., Ito K., Godoy S. Quantum Theory of Conducting Matter - Superconductivity

Подождите немного. Документ загружается.