Фирсов И.П., Семерий О.С. (сост.) Методические указания к лабораторным работам по математической статистике с применением ЭВМ
Подождите немного. Документ загружается.


41
Поскольку
() () ()
12
12
1
tt
tt
fxdx fxdx fxdx
∞
−∞
++=
∫∫∫
, то, учитывая равен-
ства (4.5) и (4.6), получим
()
1
21
t
fxdx
β
−∞
=−
∫
,
()
2
21
t
fxdx
β
∞
=
−
∫
. (4.7)
Из (4.7) найдем
1
t и
2
t , а решая неравенство
2
12
2
nS
tt
σ
<
<
, найдем
доверительный интервал
22
21
,
nS nS
l
tt
⎛⎞
=
⎜⎟
⎝⎠
.
Применение методов получения доверительных интервалов для
оценок параметров иллюстрируют примеры 4.1-4.4. В начале примера
создается выборка нормально распределенных чисел с заданными па-
раметрами (математическим ожиданием и дисперсией). Далее в доку-
менте вычисляются оценки для этих параметров по методу моментов.
Для дальнейших вычислений вводятся плотности распределений Стью-
дента,
2
χ
и нормального. Далее находятся доверительные интервалы
для математического ожидания при известной и неизвестной диспер-
сии. В следующем разделе примеров решается задача определения до-
верительного интервала для дисперсии при известном и неизвестном
математических ожиданиях.
Пример 4.1 (Mathematica)
Получение выборки с заданными
μ
и
σ
<<Statistics`ContinuousDistributions`
<<Statistics`ConfidenceIntervals`
Объём выборки
n=50;
Заданные параметры нормального закона
muX=3; sigmaX=2;
Выборка с нормальным распределением
x=RandomArray[NormalDistribution[muX,sigmaX],n];
Вычисление моментов
1-й начальный момент (оценка математического ожидания)
Mx=1/n*Apply[Plus,x]
2.91748
2-й центральный момент (оценка дисперсии)
Dx=1/n*Apply[Plus,(x-Mx)^2]
4.63328
Оценка ср. кв. отклонения
42
sigma=Sqrt[Dx]
2.1525
Плотность распределения нормального закона
fn[x_,sigma_]:=Exp[-x^2/2/sigma^2]/
Sqrt[2*Pi*sigma^2];
Плотность распределения Стьюдента
ft[t_,n_]:=Gamma[(n+1)/2]/Gamma[n/2]/
Sqrt[Pi*n]*(1+t^2/n)^(-(n+1)/2);
Плотность распределения
2
χ
fx[x_,n_]:=x^((n-2)/2)*Exp[-x/2]/2^(n/2)/
Gamma[n/2];
Случай 1. Оценка мат. ожидания при известной дисперсии
Доверительная вероятность
beta=0.95;
Заданная дисперсия
S=sigmaX^2;
sigma1=Sqrt[S/n];
Нахождение доверительного интервала
delta=z/.FindRoot[
2*Integrate[fn[y,sigma1],{y,0,z}]-beta==0,{z,0}]
0.554362
dz=delta*sigma1; m={Mx-dz,Mx+dz};
Доверительный интервал для мат. ожидания
Print["Mx=",Mx," ",m]
Mx=2.91748 {2.76068,3.07428}
Случай 2. Оценка мат. ожидания при неизвестной дисперсии
Оценка дисперсия
S=Dx;
Нахождение доверительного интервала
delta=z/.FindRoot[
2*Integrate[ft[y,n-1],{y,0,z}]-beta==0,{z,0}]
2.00958
dz=delta*Sqrt[S/n]; m={Mx-dz,Mx+dz};
Доверительный интервал для мат. ожидания
Print["Mx=",Mx," ",m]
Mx=2.91748 {2.30574,3.52921}
Случай 3. Оценка дисперсии при известном мат. ожидании
alpha=1-beta
0.05
delta1=z/.FindRoot[
Integrate[fx[y,n],{y,0,z}]-alpha/2==0,{z,n}]
32.3574
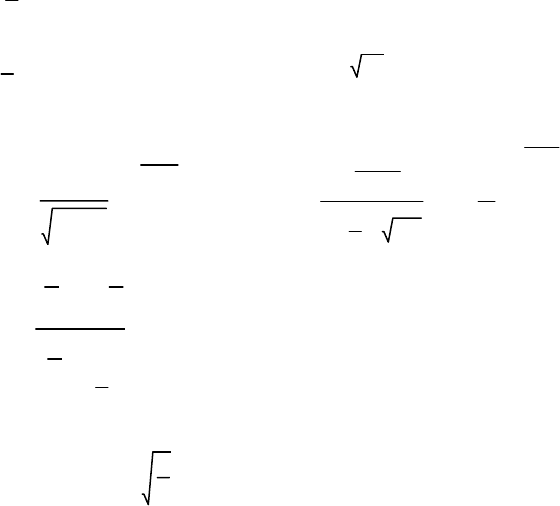
43
delta2=z/.FindRoot[
Integrate[fx[y,n],{y,z,20*n}]-alpha/2==0,{z,n}]
71.4202
dz=n*S; s={dz/delta2,dz/delta1};
Доверительный интервал для дисперсии
Print["Dx=",Dx," ",s]
Dx=4.63328 {3.24367,7.15954}
Случай 4. Оценка дисперсии при неизвестном мат. ожидании
delta1=z/.FindRoot[
Integrate[fx[y,n-1],{y,0,z}]-alpha/2==0,{z,n}]
31.5549
delta2=z/.FindRoot[
Integrate[fx[y,n-1],{y,z,2*n}]-alpha/2==0,{z,n}]
70.2173
dz=(n-1)*S; s={dz/delta2,dz/delta1};
Доверительный интервал для дисперсии
Print["Dx=",Dx," ",s]
Dx=4.63328 {3.23325,7.19477}
Пример 4.2 (Matlab)
n=50; muX=3; sigmaX=2; x=normrnd(muX,sigmaX,1,n);
Mx=1/n*sum(x)
Dx=1/(n-1)*sum((x-Mx).^2), sigma=sqrt(Dx)
fn=inline(...
'exp(-x.^2/2/sigma^2)/sqrt(2*pi*sigma^2)',...
'x','sigma');
ft=inline(strcat('gamma((n+1)/2)/gamma(n/2)/',...
'sqrt(pi*n)*(1+t.^2/n).^(-(n+1)/2)'),'t','n');
fx=inline(...
'x.^(n/2-1).*exp(-x/2)/2^(n/2)/gamma(n/2)',...
'x','n');
df1=inline('2*quad(f,0,y,[],[],theta)-lambda',...
'y','f','theta','lambda');
df2=inline('2*quad(f,y,n,[],[],theta)-lambda',...
'y','f','theta','lambda','n');
zf1=inline('fzero(df,z,[],f,theta,beta)',...
'f','df','z','theta','beta');
zf2=inline('fzero(df,z,[],f,theta,beta,n)',...
'f','df','z','theta','beta','n');
beta=0.95; S=sigmaX^2; sigma1=sqrt(S/n)
delta=zf1(fn,df1,0,sigma1,beta), dz=delta*sigma1;
Mx, m=[Mx-dz,Mx+dz]
S=Dx; delta=zf1(ft,df1,0,n-1,beta)
44
dz=delta*sqrt(S/n); Mx, m=[Mx-dz,Mx+dz]
alpha=1-beta, delta1=zf1(fx,df1,n,n,alpha)
delta2=zf2(fx,df2,n,n,alpha,5*n), dz=n*S;
Dx, m=[dz/delta2,dz/delta1]
delta1=zf1(fx,df1,n,n-1,alpha)
delta2=zf2(fx,df2,n,n-1,alpha,5*n), dz=(n-1)*S;
Dx, m=[dz/delta2,dz/delta1]
Пример 4.3 (Matcad)
n5
0
:=
i0n1
−
.
.:=
μX
3
:=
σX
2
:=
x rnorm n μX,σX,
(
)
:=
Mx
1
n
i
x
i
∑
⋅:=
Mx 2.919
=
Dx
1
n
i
x
i
Mx−
()
2
∑
⋅:=
Dx 3.203
=
σ D
x
:=
σ 1.79=
fn x σ,
()
1
2 π⋅σ
2
⋅
e
x
2
2 σ
2
⋅
−
⋅:=
ft t n,()
Γ
n1+
2
⎛
⎜
⎝
⎞
⎟
⎠
Γ
n
2
⎛
⎜
⎝
⎞
⎟
⎠
π n⋅⋅
1
t
2
n
+
⎛
⎜
⎝
⎞
⎟
⎠
n1+
2
−
⋅:=
fx x n,()
x
n
2
1−
e
x
2
−
⋅
2
n
2
Γ
n
2
⎛
⎜
⎝
⎞
⎟
⎠
⋅
:=
β 0.9
5
:=
S σX
2
:=
σ1
S
n
:=
z
0
:=
δ root 2
0
z
yfn y σ1,
()
⌠
⎮
⌡
d⋅β− z,
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
δ 0.554=
dz δσ1⋅:=
mMxdz− Mx dz+()
T
:=
Mx 2.919=
m
T
2.762 3.075()=
SD
x
:=
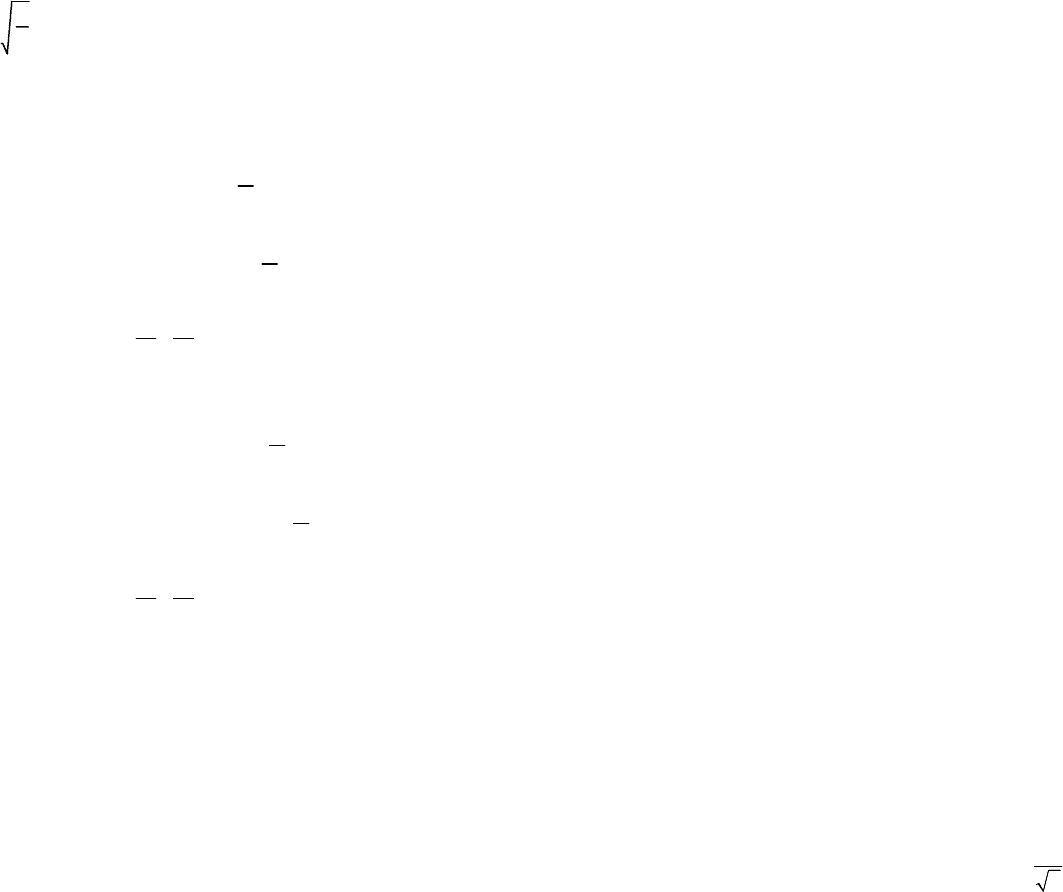
45
z
0
:=
δ root 2
0
z
yft y n 1−,()
⌠
⎮
⌡
d⋅β− z,
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
δ 2.008=
dz δ
S
n
⋅:=
mMxdz− Mx dz+()
T
:=
Mx 2.919=
m
T
2.41 3.427()=
α 1 β−:=
α 0.05=
z
n
:=
δ1 root
0
z
yfx y n,()
⌠
⎮
⌡
d
α
2
− z,
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
δ1 32.394=
z
n
:=
δ2 root
z
20 n⋅
yfx y n,()
⌠
⎮
⌡
d
α
2
− z,
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
δ2 71.394=
dz n
S
⋅:=
s
dz
δ2
dz
δ1
⎛
⎜
⎝
⎞
⎟
⎠
T
:=
Dx 3.203=
s
T
2.244 4.945()=
z
n
:=
δ1 root
0
z
yfx y n 1−,()
⌠
⎮
⌡
d
α
2
− z,
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
δ1 31.584=
z
n
:=
δ2 root
z
20 n⋅
yfx y n 1−,()
⌠
⎮
⌡
d
α
2
− z,
⎛
⎜
⎜
⎝
⎞
⎟
⎟
⎠
:=
δ2 70.201=
dz n 1−()
S
⋅
:=
s
dz
δ2
dz
δ1
⎛
⎜
⎝
⎞
⎟
⎠
T
:=
Dx 3.203=
s
T
2.236 4.97()=
Пример 4.4 (Maple)
> restart: with(stats): with(describe):
randomize():
> n:=50: muX:=3: sigmaX:=2:
> x:=[random[normald[muX,sigmaX]](n)]:
> Mx:=moment[1](x);
> Dx:=moment[2,mean,0](x); sigma:=sqrt(Dx);
> fn:=(x,sigma)->exp(-x^2/2/sigma^2)/
sqrt(2*Pi*sigma^2):
46
> ft:=(t,n)->GAMMA((n+1)/2)/GAMMA(n/2)/
sqrt(Pi*n)*(1+t^2/n)^(-(n+1)/2);
> fx:=(x,n)->x^((n-2)/2)*exp(-x/2)/2^(n/2)/
GAMMA(n/2);
> beta:=0.95:
> S:=sigmaX^2: sigma1:=evalf(sqrt(S/n));
> delta:=fsolve(2*int(fn(y,sigma1),y=0..z)-beta,z);
> dz:=delta*sigma1: m:=[Mx-dz, Mx+dz]: 'Mx'=Mx, m;
> S:=Dx:
> delta:=fsolve(2*int(ft(y,n-1),y=0..z)-beta,z);
> dz:=delta*sqrt(S/n): m:=[Mx-dz, Mx+dz]:
> 'Mx'=Mx, m;
> alpha:=1-beta;
> delta1:=fsolve(int(fx(y,n),y=0..z)-alpha/2,z);
> delta2:=fsolve(int(fx(y,n),y=z..20*n)-alpha/2,z);
> dz:=n*S: s:=[dz/delta2, dz/delta1]: 'Dx'=Dx, s;
> delta1:=fsolve(int(fx(y,n-1),y=0..z)-alpha/2,
z,0..n);
> delta2:=fsolve(int(fx(y,n-1),y=z..20*n)-alpha/2,
z,n..20*n);
> dz:=(n-1)*S: s:=[dz/delta2, dz/delta1]:
> 'Dx'=Dx, s;
Задание
1. В условиях примера 1 записать формулы доверительного интервала
математического ожидания
ma
ξ
=
, считая дисперсию
2
σ
извест-
ной.
2.
В условиях примера 1 записать формулы для доверительного ин-
тервала дисперсии
2
D
ξ
σ
= , считая математическое ожидание из-
вестной величиной.
3.
Используя выборку из примера 2.1 (первая часть) и полагая, что
доверительная вероятность
0,8; 0, 9; 0, 95,
β
=
вычислить довери-
тельные интервалы:
1) для математического ожидания, считая дисперсию: а) известной
величиной
22
S
σ
=
, б) неизвестной величиной (использовать оценку);
2) для дисперсии, считая математическое ожидание а) известной
величиной
mMx
ξ
=
, в) неизвестной величиной. Результаты сравнить.
Указание к заданию 1. Учесть, что статистика
(
)
,
n
txa Mxa
=
− рас-
пределена по нормальному закону
0,N
n
σ
⎛⎞
⎜⎟
⎝⎠
.
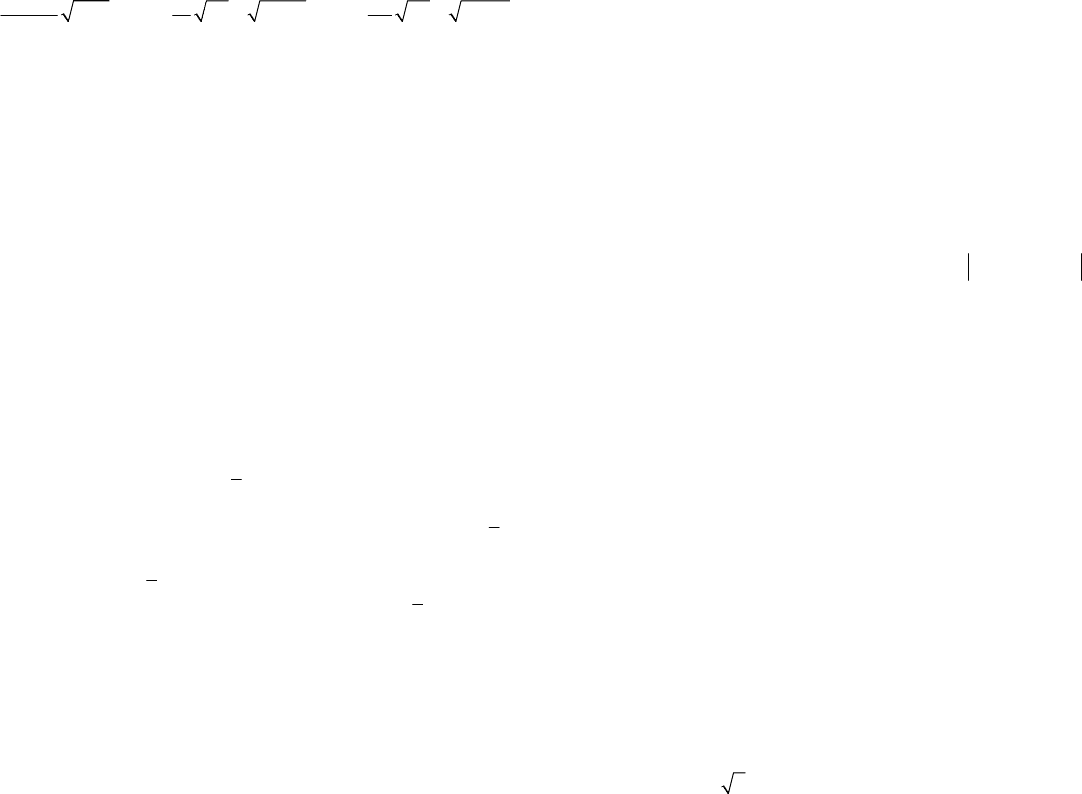
47
Указание к заданию 2. Рассмотреть статистику
(
)
222
,/
n
tx nS
σ
σ
∗
= .
Замечание к заданию 3. Считать, что генеральная совокупность, из
которой взята выборка, распределена по нормальному закону. При этом
в случае больших
n распределения
2
χ
и Стьюдента сходятся к нор-
мальному закону, поэтому при
30n > можно считать, что статисти-
ки
1
n
Mx a
n
S
t
−
=−
, 221
S
n
nn
t
σ
∗
=−−, 223
n
S
nn
t
σ
=
−− рас-
пределены по нормальному закону
()
0,1N .
4.
Провести расчеты доверительных интервалов для
μ
и
σ
, заданных
преподавателем (смотри примеры 4.1-4.4), при объеме выборок 10,
50 и 100.
Контрольные вопросы
1. Что называется доверительным интервалом и доверительной веро-
ятностью?
2.
Дайте общую схему построения доверительного интервала.
3.
Как изменяется доверительный интервал с увеличением надежно-
сти? С увеличением объема выборки?
4.
Как изменяется доверительный интервал в зависимости от того,
известны ли другие параметры точно или нет?
Выборочные оценки в задачах 5-8 определялись по результатам
n
наблюдений. Используя эти данные, найти 90%-ные и 99%-ные
доверительные интервалы для математического ожиданияследующих
характеристик (Задачи № 3.1–3.4 гл.15 [2]):
5.
Ёмкость конденсатора, если 20x = мкФ, 16n
=
, с.к.о. известно и
равно 4 мкФ.
6.
Время безотказной работы электронной лампы, если 500x
=
,
100n = , с.к.о. известно и равно 10 ч.
7.
Диаметр вала, если 30x = мм, 9n = ,
2
9s
=
мм
2
.
8.
Содержание углерода в единице продукта, если 18x
=
г, 25n
=
,
4s = г.
48
5. Equation Section (Next)Критерии согласия
Допустим, что построенную по выборке статистическую функцию
распределения
(
)
n
F
x мы сгладили с помощью некоторой гипотетиче-
ской функции распределения
(
)
F
x . Возникает вопрос: а верна ли гипо-
теза о том, что функция распределения именно
(
)
F
x
, а не какая-либо
другая? Точнее, не противоречит ли гипотеза о законе распределения
()
F
x
результатам эксперимента? Чтобы ответить на этот вопрос, поль-
зуются критериями согласия.
Под критерием согласия понимают некоторую величину
(
)
,
n
F
FΔ
,
которая отражает количественную меру расхождения гипотетического
()
F
x
и эмпирического
(
)
n
F
x
распределений. Эту величину можно
выбрать многими способами, в соответствии с которыми получаются и
различные критерии проверки интересующей нас гипотезы. Например,
можно положить
(
)
(
)
(
)
,sup
nnn
F
FD FxFxΔ== −
(5.1)
или
( ) () () ()
2
2
,
nn
F
FFxFxdFx
ω
∞
−∞
Δ== −
⎡⎤
⎣⎦
∫
.
В первом случае получаем критерий Колмогорова, во втором – кри-
терий Мизеса.
Схема применения критерия согласия следующая. Возьмём
0
α
>
настолько малым, чтобы осуществление события с вероятностью
α
можно было считать практически невозможным в единичном опыте.
Зная закон распределения случайной величины
(
)
,
n
F
FΔ=Δ
, найдем ее
возможное значение
0
Δ
из уравнения
(
)
0
P
α
Δ
>Δ = . По данной вы-
борке вычислим значение критерия согласия
(
)
1
,
n
F
FΔ=Δ . Если ока-
жется, что
10
Δ
>Δ , то это значит, что произошло практически неверо-
ятное событие. Следовательно, эксперимент опровергает нашу гипоте-
зу, и она отбрасывается. При этом вероятность того, что мы отбросили
верную гипотезу, равна
α
. Если
10
Δ
<Δ , то гипотеза не противоречит
эксперименту и должна быть принята. Число
α
называется уровнем
значимости критерия.
Колмогоров нашел предельную функцию распределения величины
n
nD
λ
= . Эту функцию обычно обозначают
(
)
K
x :

49
()
()
()
22
2
lim 1
k
kx
n
n
k
Kx P nD x e
∞
−
→∞
=−∞
=<=−
∑
, 0x > . (5.2)
Формулой (5.2) можно пользоваться для больших
n
.
Чтобы воспользоваться критерием согласия Колмогорова, нужно
построить графики гипотетической и выборочной функций распределе-
ния, по графикам найти статистику
n
D и вычислить величину
1 n
nD
λ
= . Найти вероятность события
1n
nD
λ
> по формуле
()
() ( )
22
1
2
11
1
121
k
k
n
k
PnD K e
λ
λλ
∞
−
=
>=− =− −
∑
. (5.3)
Если эта вероятность меньше
α
, то гипотеза отвергается, если
больше, то признается непротиворечащей эксперименту.
Предположим теперь, что, например, из физических соображений
мы можем высказать гипотезу только о виде закона распределения, а
параметры, входящие в него, неизвестны. Тогда критерий согласия
Колмогорова не применим. В таких случаях часто используют критерий
согласия Пирсона.
Всю числовую ось разобьем на
r непересекающихся разрядов точ-
ками
012
...
r
xxx x−∞=<<<<=∞. Примем гипотезу о функции рас-
пределения. Неизвестные параметры, входящие в нее, заменим их
оценками. Таким образом, гипотетическая функция распределения
(
)
F
x будет известна, и можно будет найти вероятности
()
(
)
1ii i
pFx Fx
−
=−
попадания случайной величины в i -й разряд.
Возьмем статистику
()
2
2
1
r
ii
n
i
i
mnp
t
np
χ
=
−
==
∑
. (5.4)
Здесь
n – объем выборки, r – число разрядов,
i
m – число значений в
i -м разряде.
За меру расхождения между гипотетической
(
)
F
x
и эмпирической
()
n
F
x функциями распределения примем статистику
(
)
,
nn
tFF=Δ ,
определенную формулой (5.4). Фишером доказано, что предельным
законом распределения статистики
n
t является распределение
2
χ
с
1rm−− степенями свободы, если параметры оценены по методу мак-
симального правдоподобия. Здесь
m – число параметров, входящих в
гипотетическую функцию распределения. Доказано также, что при объ-
еме выборки
30n > с достаточной точностью можно пользоваться пре-
дельным законом распределения, если
5
i
np > .
50
Схема применения критерия Пирсона следующая. По формуле (5.4)
вычисляют значение статистики
0n
t
=
Δ . Вычисляют вероятность
()()
0
0
pfxdx
∞
Δ
Δ>Δ =
∫
. (5.5)
Здесь
()
f
x определяется формулой (2.5), а n следует заменить на
1rm
−
− . Если эта вероятность меньше уровня значимости
α
, то гипо-
тезу следует отбросить.
Применение критериев согласия иллюстрируют примеры 5.1-5.4. В
начале генерируется (по методу обратных функций) выборка значений
случайной величины, распределенной по показательному закону с за-
данным параметром
a . Далее выборка группируется и находится груп-
пированная функция распределения, что необходимо для критерия
Колмогорова. В соответствии со схемой применения критерия Колмо-
горова, задается теоретическая функция распределения
(
)
F
x , и по
этим значениям вычисляется статистика
n
D . Вычисляется вероятность
по формуле (5.3) и сравнивается с уровнем значимости
α
.
В следующем разделе примеров применяется критерий Пирсона,
Отметим, что, поскольку критерий Пирсона работает с плотностью рас-
пределения, для него может понадобиться другая группировка той же
исходной выборки. Теоретическая плотность распределения может
быть получена дифференцированием ранее введенной функции распре-
деления. Теперь можно вычислить значение статистики и оценить веро-
ятность (5.5), сравнивая ее
с уровнем значимости
α
.
Пример 5.1 (Matlab)
% Часть 1. Критерий Колмогорова
% Получение выборки заданного объема
n
n=100;
% Теоретическая функция распределения
f=inline('1-exp(-a*x)','x','a');
% Теоретическая плотность распределения
df=inline('a*exp(-a*x)','x','a');
% Обратная функция распределения
g=inline('-log(1-x)/a','x','a');
% Параметр закона распределения
a=2;
% Равномерно распределённые случайные числа
eps=1*1e-2; Y=unifrnd(0,1-eps,1,n);
% Числа, распределённые по показательному закону
X=g(Y,a);

51
% Группировка для критерия Колмогорова
% Вариационный ряд
Y=sort(X);
% Число разрядов для группировки
k=10;
% Размах выборки
R=Y(n)-Y(1)
R=2.0231
% Длина разряда
h=R/k
h=0.2023
% Определение абсолютных частот и середин разрядов
[m,xs]=hist(Y,k);
% Относительные частоты
p=m/n;
% Накопленные частоты
Fg=cumsum(p);
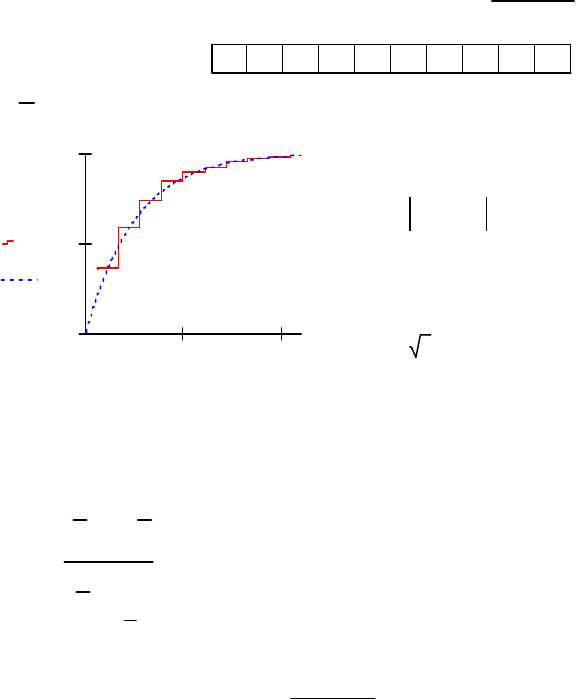
% График эмпирической функций распределения
stairs(xs,Fg), hold on
% График теоретической функций распределения
x1=Y(1):0.1:Y(n); y1=f(x1,a);
plot(x1,y1,'r'), hold off, pause
% Уровень значимости
alpha=0.05;
Ft=f(xs,a);
epsilon=abs(Ft-Fg);
Dn=max(epsilon)
Dn=0.1466
lambda1=sqrt(k)*Dn
lambda1=0.4637
52
j=1:n; PL=-2*sum((-1).^j.*exp(-2*j.^2*lambda1^2))
PL=0.9826
if PL>alpha
sprintf('Гипотеза не противоречит эксперименту')
else
sprintf('Гипотеза противоречит эксперименту')
end
Гипотеза не противоречит эксперименту
% Часть 2. Критерий Пирсона
% Теоретические вероятности
pr=df(xs,a)*h;
chi2=n*sum((p-pr).^2/pr)
chi2=0.1360
% Плотность распределения хи-квадрат
fx=inline(...
't.^(n/2-1).*exp(-t/2)/2^(n/2)/gamma(n/2)',...
't','n');
dfx=inline('quad(f,0,y,[],[],n)-(1-alpha)',...
'y','f','n','alpha');
zx=inline('fzero(df,z0,[],f,n,alpha)',...
'f','df','n','alpha','z0');
r=k-1;
w=zx(fx,dfx,r,alpha,r)
w=16.9190
if chi2<w
sprintf('Гипотеза
не противоречит эксперименту')
else
sprintf('Гипотеза противоречит эксперименту')
end
Гипотеза не противоречит эксперименту
Пример 5.2 (Mathcad)
n10
0
:=
j0n1
−
.
.:=
a
2
:=
ε 10
2
−
:=
fx( ) 1 exp a
−
x
⋅
()−:=
gx()
ln 1 x
−
()
a
−:=
df x()
x
fx()
d
d
:=
Y runif n 0, 1 ε−,
(
)
:=
X
j
gY
j
(
)
:=
Y sort X():=
RY
n1−
Y
0
−
:=
R 2.186
=
k1
0
:=
i0k1
−
.
.:=
h
R
k
:=
h 0.219
=
53
xr
0
Y
0
:=
xr
i1+
xr
i
h
+:=
xr
k
xr
k
10
4
−
+:=
xs
i
xr
i1+
xr
i
+
2
:=
m hist xr Y
,
():=
m
T
36231511523212
=
p
m
n
:=
Fg
0
p
0
:=
j1k1−..:=
Fg
j
Fg
j1−
p
j
+
:=
12
0.5
1
Fg
i
fy()
xs
i
y,
α 0.0
5
:=
Ft
i
fxs
i
(
)
:=
ε
i
Ft
i
Fg
i
−:=
Dn max ε
(
)
:=
Dn 0.159
=
λ1kD
n
⋅:=
λ1 0.504=
j1
n
..:=
PL 2−
j
1−()
j
exp 2− j
2
⋅λ1
2
⋅
(
)
⋅
∑
⎡
⎢
⎢
⎣
⎤
⎥
⎥
⎦
⋅:=
PL 0.961
=
if PL α> "True", "False",
()
"True"=
fx x n,()
x
n
2
1−
e
x
2
−
⋅
2
n
2
Γ
n
2
⎛
⎜
⎝
⎞
⎟
⎠
⋅
:=
rk1
−
:=
pr
i
df xs
i
(
)
h
⋅
:=
χ2n
i
p
i
pr
i
−
()
2
pr
i
∑
⋅:=
χ2 4.165=
y
r
:=
w root
0
y
xfx x r,()
⌠
⎮
⌡
d1α−
()
− y,
⎡
⎢
⎢
⎣
⎤
⎥
⎥
⎦
:=
w 16.893
=
if χ2w< "True", "False",
()
"True"=
Пример 5.3 (Maple)
> restart: with(stats): with(transform):
randomize():
54
> n:=100:
> f:=x->1-exp(-a*x);
> df0:=diff(f(x),x): df:=unapply(df0,x);
> g0:=solve(f(x)=y,x): g:=unapply(g0,y);
> a:=2:
> eps:=1e-2: Y:=[random[uniform[0,1-eps]](n)]:
> X:=map(g,Y): Y:=sort(X):
> k:=10: R:=Y[n]-Y[1]; h:=R/k;
> xr:=[Y[1]+i*h $i=0..k]: xr[k+1]:=xr[k+1]+1e-4:
> xrr:=[(xr[i]..xr[i+1]) $i=1..k]:
> xs:=evalf([xr[i]+0.5*h $i=1..k],3):
> xp:=scaleweight[1/n](statsort(tallyinto(Y,xrr))):
> p:=evalf(frequency(xp),3):
> F:=x->sum(p[i]*Heaviside(x-xs[i]),i=1..k):
> plot([F,f],Y[1]..Y[n],0..1,labels=['Y','F']);
> alpha:=0.05:
> Fg:=cumulativefrequency(xp): Ft:=map(f,xs):
> epsilon:=map(abs,Ft-Fg):
> Dn:=max(op(epsilon));
> lambda1:=evalf(sqrt(k)*Dn);
> PL:=-2*sum((-1)^j*exp(-2*j^2*lambda1^2),j=1..n);
> `if`(PL<alpha,'false','true');
> pr:=map(df,xs)*h:
> chi2:=n*sum((p[i]-pr[i])^2/pr[i],i=1..k)/n;
> fx:=(x,n)->x^((n-2)/2)*exp(-x/2)/2^(n/2)/
GAMMA(n/2);
> r:=k-1:
> w:=fsolve(int(fx(t,r),t=0..y)-(1-alpha),y);
> `if`(chi2<w,'true','false');
Пример 5.4 (Mathematica)
<<Calculus`DiracDelta`; <<Graphics`Colors`
<<Statistics`ContinuousDistributions`
<<Statistics`DataManipulation`
n=100; a=2; eps=0.01;
f[x_]:=1-Exp[-a*x]; df[x_]=D[f[x],x];
g[x_]:=-Log[1-x]/a;
Y=RandomArray[UniformDistribution[0,1-eps],n];
X=Map[g,Y]; Y=Sort[X];
k=10; R=Y[[n]]-Y[[1]]; h=R/k
xs=Table[Y[[1]]+(i-1/2)*h,{i,k}];
m=BinCounts[Y,{Y[[1]],Y[[n]],h}]; m[[1]]+=1; m
p=N[m/n];

55
F[y_]:=Sum[p[[i]]*UnitStep[y-xs[[i]]],{i,k}];
Plot[{F[y],f[y]},{y,Y[[1]],Y[[n]]},
PlotStyle->{Red,Green}];
alpha=0.05;
Fg=CumulativeSums[p]; Ft=Map[f,xs];
epsilon=Abs[Ft-Fg];
Dn=Max[epsilon]
lambda1=Sqrt[k]*Dn
PL=-2*Sum[(-1)^j*Exp[-2*j^2*lambda1^2],{j,n}]
If[PL>alpha,"true","false"]
pr=df[xs]*h;
chi2=n*Sum[(p[[i]]-pr[[i]])^2/pr[[i]],{i,k}]
fx[x_,n_]:=x^((n-2)/2)*Exp[-x/2]/2^(n/2)/
Gamma[n/2];
r=k-1;
w=z/.FindRoot[
Integrate[fx[y,r],{y,0,z}]-(1-alpha)==0,{z,r}]
If[chi2<w,"true","false"]
Задание
1. Получить выборку значений случайной величины, распределенной
по показательному закону с заданным параметром
a .
2.
Используя критерий согласия Колмогорова, проверить гипотезу о
том, что генеральная совокупность, выборка которой получена ра-
нее, распределена по закону
()
1
ax
F
xe
−
=− . Уровень значимости
0, 05
α
= .
3.
Используя критерий согласия Пирсона, проверить гипотезу о за-
данном распределении той же генеральной совокупности. Критерий
значимости
0, 05
α
=
.
4.
Провести расчеты по документу для объемов выборок 20, 50 и 100.
Контрольные вопросы
1. Что такое критерий согласия?
2.
Какие критерии согласия Вы знаете?
3.
Опишите схему применения критериев согласия Колмогорова и
Пирсона.
4.
Запишите плотность распределения закона
2
χ
с 1nm
−
− степенью
свободы.
5.
Могут ли опытные данные одновременно согласовываться с не-
сколькими гипотезами о законе распределения?
6.
Решить задачи № 6.8, 6.12–6.16 гл. 15[2].
56
6. Equation Section (Next)Зависимость случайных
величин, регрессия.
Оценка регрессии методом наименьших квадратов
Рассмотрим двумерную случайную величину
(
)
,
ξ
η
, т.е. упорядо-
ченную пару случайных величин. Пусть, например,
ξ
– диаметр де-
ревьев некоторого леса, а
η
– высота деревьев. Тогда m
ξ
и m
η
– сред-
ние диаметр и высота деревьев, а
ξ
σ
и
η
σ
характеризуют разброс диа-
метра и высоты относительно средних значений.
Интуитивно ясно, что диаметр и высота деревьев связаны некото-
рой зависимостью, однако эта зависимость не является функциональ-
ной, так как для деревьев, имеющих одинаковый диаметр
x
ξ
=
высота
η
является величиной случайной. Такую зависимость называют веро-
ятностной или стохастической. Однако можно говорить о функцио-
нальной зависимости средней высоты деревьев от диаметра
()
(
)
M
xgx
η
=
. Здесь
(
)
M
x
η
– условное математическое ожидание,
т.е. средняя высота деревьев, имеющих диаметр
x
. Если
(
)
2
f
x
η
– ус-
ловная плотность распределения
η
, то
()
()
()
2
M
xgx yfyxdy
η
∞
−∞
==
∫
. (6.1)
Аналогично
()
()
()
1
M
yqy xfxydx
ξ
∞
−∞
==
∫
. (6.2)
Здесь
(
)
M
y
ξ
– средний диаметр деревьев высотой y . Функции
()
y
gx= и
(
)
x
qy= , определенные формулами (6.1) и (6.2), называют-
ся соответственно регрессией величины
η
на
ξ
и регрессией величины
ξ
на
η
. Графики этих линий называются кривыми регрессии. Плотно-
сти распределения
(
)
1
f
x и
(
)
2
f
y (компоненты двумерной случайной
величины) и условные плотности распределения связаны с плотностью
()
,
f
xy двумерной случайной величины формулой
(
)
(
)
(
)
12 21
,() ()
f
xy f xf yx f y f xy==. (6.3)
Если
η
и
ξ
связаны функциональной зависимостью, то при
x
ξ
=
величина
η
принимает единственное значение
(
)
g
x
η
= . При
вероятностной зависимости будет неизбежно наблюдаться рассеяние
η

57
ностной зависимости будет неизбежно наблюдаться рассеяние
η
около
центра
(
)
g
x . Мерой этого рассеяния естественно считать условную
дисперсию
()
()
()
()
2
2
Dx ygxfyxdy
η
∞
−∞
=−
∫
. (6.4)
Величину
(
)
Dx
η
можно рассматривать как среднюю квадратич-
ную погрешность оценки величины
η
по наблюдаемому значению
x
случайной величины
ξ
, если за оценку берется регрессия
(
)
g
x . Эта
погрешность зависит от
x
, т.е. от закона распределения
ξ
. Чтобы по-
лучить представление о точности оценки во всем диапазоне изменения
ξ
, величину
(
)
Dx
η
усредняют. С учетом (6.3) и (6.4) получим
()
() ()
()
()
()
()
()
() ()
()
2
221
22
,.
D x f x dx y g x f y x f x dxdy
ygx fxydxdy M gx
δη
η
∞∞
−∞ −∞
∞
−∞
==− =
=− =−
∫∫∫
∫∫
(6.5)
Известно, что рассеяние, определяемое средним квадратом откло-
нения, минимально, если его вычислять относительно центра рассея-
ния. Отсюда следует, что величина
()
()
2
M
gx
δη
=− принимает свое
минимальное значение. Другими словами, регрессия
η
на
ξ
является
наилучшей (в смысле минимума среднего квадратичного отклонения)
оценкой зависимости
η
от
ξ
.
Очевидно, что регрессия может служить оценкой зависимости, ко-
гда эта регрессия известна. Если регрессия неизвестна, то ищут оценку
η
в некотором классе функций случайной величины
ξ
и вместо (6.5)
требуют минимума величины
()
()
2
My
εηξ
=−
%
. (6.6)
Оценка
(
)
y
ξ
%
случайной величины
η
, принадлежащая определен-
ному классу функций и доставляющая минимум величине
η
, опреде-
ляемой формулой (6.6), называется средней квадратичной регрессией
η
на
ξ
.
Будем, например, искать оценку
(
)
y
ξ
%
среди класса линейных
функций, т.е.
(
)
y
ξ
αβξ
=+
%
. Коэффициенты
α
и
β
найдем из условия
минимума
ε
, т.е. методом наименьших квадратов. Преобразуем снача-
58
ла (6.6) следующим образом:
()
()()( )
()
2
2
2
222
2.
M
Mm mm m
mmK
ηξηξ
ηξη ξ ξη
εηαβξ
ηβξ αβ
σβσ αβ β
=−−=
⎡⎤
=−−−+−− =
⎣⎦
=+ + −− −
(6.7)
Здесь
(
)
(
)
KM m m
ξη ξ η
ξη
⎡
⎤
=−−
⎣
⎦
– корреляционный момент слу-
чайных величин
ξ
и
η
.
Необходимыми условиями минимума функции (6.7) являются
0
ε
α
∂
=
∂
, 0
ε
β
∂
=
∂
или
2
0,
0.
mm
K
ηξ
ξξη
αβ
βσ
−
−=
⎧
⎪
⎨
−=
⎪
⎩
(6.8)
Решая систему (6.8), найдем
α
,
β
и вместе с тем линейную оценку
регрессии
()
()
.ymm
η
ηξ
ξ
σ
ξαβξ ρ ξ
σ
=+ = + −
%
(6.9)
Здесь
K
ξ
η
ξ
η
ρ
σ
σ
= – коэффициент корреляции. Линия
()
ym xm
η
η
ξ
ξ
σ
ρ
σ
=+ − (6.10)
называется прямой линией регрессии
η
на
ξ
. Коэффициент
1
η
ξ
σ
βρ
σ
=
называется коэффициентом регрессии.
Аналогично можно получить прямую регрессии
ξ
на
η
()
x
mym
ξ
ξ
η
η
σ
ρ
σ
=+ − . (6.11)
Прямые (6.10) и (6.11) не совпадают, но обе проходят через центр
распределения
(
)
,mm
ξ
η
. Коэффициент корреляции
ρ
служит мерой
линейной корреляционной связи между
ξ
и
η
. Если 1
ρ
=
± , то
ξ
и
η
связаны линейной функциональной зависимостью, если
0
ρ
=
, то они
не коррелированы. Прямые регрессии в этом случае параллельны осям
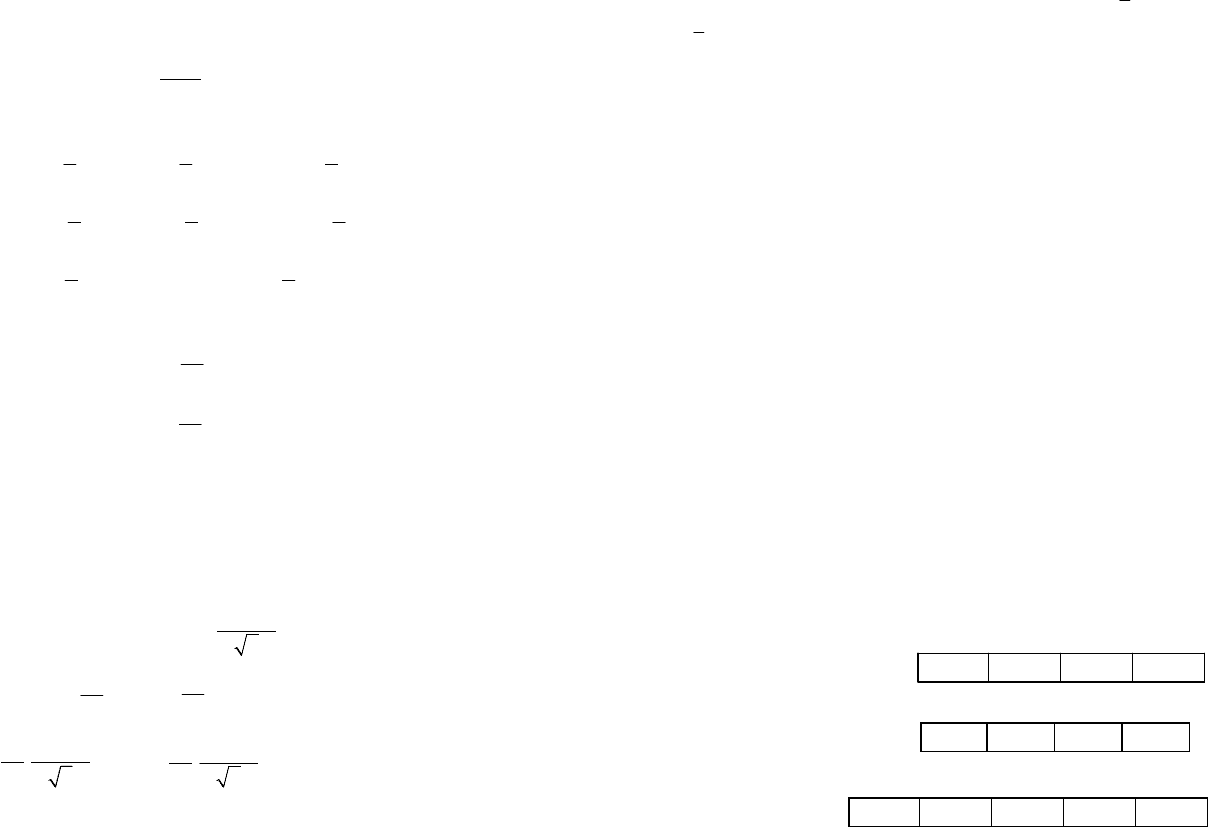
59
координат.
Если числовые характеристики, входящие в уравнения регрессии,
неизвестны, то их заменяют оценками
x
mM
ξ
=
;
y
mM
η
=
;
x
S
ξ
σ
=
;
y
S
η
σ
= ;
x
y
K
K
ξη
=
;
x
y
x
y
K
r
SS
ρ
==
,
где
1
1
n
x
i
i
M
x
n
=
=
∑
;
()
2
222
11
11
nn
x
ix i x
ii
SxM xM
nn
==
=−=−
∑∑
;
1
1
n
yi
i
M
y
n
=
=
∑
;
()
2
222
11
11
nn
yiy iy
ii
SyM yM
nn
==
=−=−
∑∑
(6.12)
()
()
11
11
nn
x
yixiyiixy
ii
K
xM yM xyMM
nn
==
=−−= −
∑∑
.
В результате получим эмпирические прямые регрессии
()
()
y
yx
x
x
x
y
y
S
yM r xM
S
S
x
Mr yM
S
=+ −
=+ −
. (6.13)
Задача нахождения регрессии тесно связана с задачей сглаживания
экспериментально полученной зависимости по методу наименьших
квадратов. В подтверждение этого можно сравнить формулы (6.13) и
(1.9).
Если генеральная совокупность имеет нормальное распределение,
то можно считать при
30n ≥ выборочный коэффициент корреляции r
нормально распределенным:
2
(1 )
,
r
Nr
n
⎛⎞
−
⎜⎟
⎝⎠
. Выборочные коэффициен-
ты регрессии
1
y
x
S
br
S
=
и
2
x
y
S
br
S
=
также распределены нормально:
2
1
(1 )
,
y
x
S
r
Nb
S
n
⎛⎞
−
⎜⎟
⎝⎠
,
2
2
(1 )
,
x
y
S
r
Nb
S
n
⎛⎞
−
⎜⎟
⎜⎟
⎝⎠
.
Учитывая это, можно легко построить доверительные интервалы
для
ρ
,
1
β
и
2
β
.
Линейная регрессия имеет важное практическое значение,
поскольку генеральная совокупность чаще всего распределена
нормально. В противном случае возможна нелинейная регрессия, а при
большом диапазоне изменения величин линеаризация регрессии
60
неправомерна. В этом случае поступают следующим образом. Для
каждого
i
x
выборки вычисляют среднее значение
i
y . Наносят точки
(
)
,
ii
x
y и соединяют их ломаной линией. По этой ломаной линии
решают вопрос о виде нелинейной зависимости. Затем проводят
сглаживание.
Следующие примеры демонстрируют применение методов нахож-
дения регрессии. Для моделирования стохастической зависимости ге-
нерируется массив нормально распределенных значений
x
и массив
случайных величин v с нулевым математическим ожиданием (помеха).
Величина
y получается путем суммирования значений
x
и помехи
v
.
Изменяя параметр
σ
для помехи v, можно регулировать степень слу-
чайности связи величин x и y , что оценивается визуально по виду гра-
фика, на котором наносятся точки.
По данным из массивов
x
и y строятся эмпирические прямые рег-
рессии. Для этого вычисляются оценки необходимых числовых харак-
теристик и строятся прямые. Для сравнения здесь же еще раз приводит-
ся график исходных данных.
Поскольку в данном случае коэффициент корреляции и выбороч-
ные коэффициенты регрессии распределены по нормальному закону,
задаем надежность и определяем доверительные интервалы путем ре-
шения соответствующих функциональных уравнений.
Пример 6.1 (Mathcad)
Получение выборок объёма n для нормально распределённых случайных
величин
X
и Y с заданными параметрами
μ
и
σ
n2
0
:=
i0n1
−
.
.:=
μX1
0
:=
σX
2
:=
μV
0
:=
σV
2
:=
Получение выборки в массиве
x
x rnorm n μX,σX,
(
)
:=
x
T
9.961 10.064 10.53 10.983
=
Вспомогательная случайная величина
v rnorm n μV,σV,
(
)
:=
v
T
-0.818 -1.348 -0.264 2.036
=
Получение выборки в массиве y
yx
v
+:=
y
T
9.143 8.716 10.266 13.019 10.838
=
Изображение полученных точек
