Фирсов И.П., Семерий О.С. (сост.) Методические указания к лабораторным работам по математической статистике с применением ЭВМ

Подождите немного. Документ загружается.

В лабораторной работе закон распределения задается функцией

арктангенса с параметрами

a и

a :

() ()

arctg

Fx a ax

=++, (2.8)

Значения параметров задаются преподавателем.

Следующие разделы примеров показывают, как по заданной

выборке вычисляются эмпирические характеристики исследуемой

случайной величины. Результатом вычислений примеров являются

таблицы значений эмпирической функции распределения

g и середин

разрядов

s .

По этим данным необходимо решить задачу методом наименьших

квадратов для двухпараметрической функции (2.8).

В случае, когда задачи получения и обработки выборки и

аппроксимации функции распределения решены правильно,

полученные при аппроксимации значения оценок параметров

будут близки к значениям параметров, заданных при получении

выборки, что легко проверить.

Пример 2.1 (Maple)

Часть 1. Обработка выборки малого объёма

> restart: with(stats): with(transform):

randomize():

Исходная выборка

> x:=[10,10,10,30,20,12,10,12,20,10]:

Объём выборки

> n:=nops(x):

Вариационный ряд для исходной выборки

> Y:=sort(x);

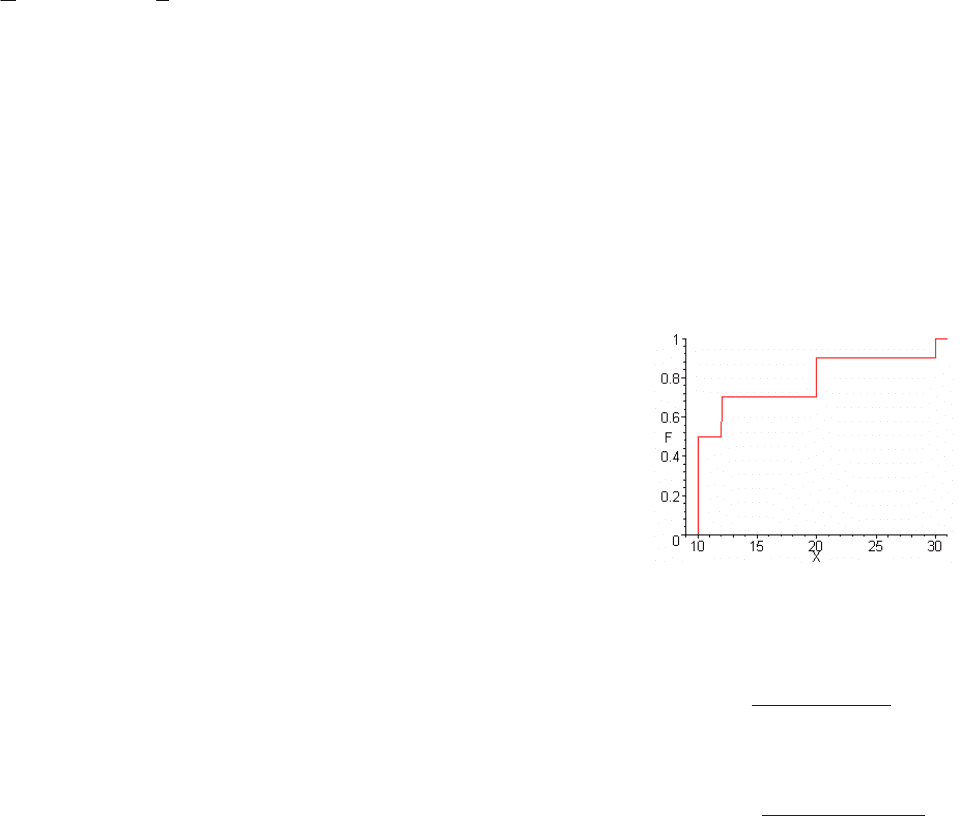
:= Y [],,,,,,,,,10 10 10 10 10 12 12 20 20 30

Построение статистического ряда для исходной выборки

Группировка повторяющихся элементов

> xm:=tally(Y);

m [],,,()Weight ,10 5 ( )Weight ,12 2 ( )Weight ,20 2 30

Неповторяющиеся элементы

> X:=statvalue(xm);

[],,,10 12 20 30

Количество неповторяющихся элементов

> k:=nops(X):

Абсолютные частоты для элементов вектора

> m:=frequency(xm);

:= m [],,,5221

Относительные частоты

> p:=evalf(m/n,1);

:= p [],,,.5 .2 .2 .1

Статистический ряд для исходной выборки

> 'X'=X,'p'=p;

[],,,10 12 20 30

= p [],,,.5 .2 .2 .1

> xp:=evalf(scaleweight[1./n](xm),1);

p [],,,()Weight ,10 .5 ( )Weight ,12 .2 ( )Weight ,20 .2 ( )Weight ,30 .1

Статистическая функция распределения

> F:=y->sum(p[i]*Heaviside(y-X[i]),i=1..k);

:= F → y

∑

= i 1

()Heaviside − yX

График статистической функции распределения

> plot(F,X[1]-1..X[k]+1,0..1,labels=['X','F']);

Часть 2. Обработка выборки большого объёма с группировкой

Объём выборки

> n:=500:

Заданная функция распределения

> f:=x->arctan(a[0]+a[1]*x)/Pi+0.5;

:= f → x +

()arctan

+ a

Плотность распределения

> df0:=diff(f(y),y): df:=unapply(df0,y);

:= df → y

() + 1( ) + a

Обратная функция распределения

> g0:=solve(f(y)=z,y): g:=unapply(g0,z);

:= g → z −1.

+ a

()cot 3.141592654

Параметры закона распределения

> a[0]:=0: a[1]:=10:

Равномерно распределённые случайные числа

> eps:=1e-2: Y:=[random[uniform[0+eps,1-eps]](n)]:

Числа, распределённые по закону арктангенса

> X:=map(g,Y):

Вариационный ряд

> Y:=sort(X):

Число разрядов для группировки

> k:=10:

Размаха выборки

> R:=Y[n]-Y[1];

5.18394458

Длина разряда

> h:=R/k;

:= h .518394458

Границы разрядов

> xr:=[Y[1]+i*h $i=0..k]: xr[k+1]:=xr[k+1]+1e-4:

Интервалы разрядов

> xrr:=[(xr[i]..xr[i+1]) $i=1..k]:

Середины разрядов

> xs:=evalf([xr[i]+0.5*h $i=1..k],3);

s [], , , , ,,,,,-2.33 -1.81 -1.29 -.771 -.254 .265 .783 1.30 1.82 2.34

Группированный статистический ряд

> xp:=scaleweight[1/n](statsort(tallyinto(Y,xrr))):

Гистограмма

> pic2:=statplots[histogram](xp):

> plots[display](plot(df,Y[1]..Y[n]),pic2);

Относительные частоты

> p:=evalf(frequency(xp),3);

:= p [], ,,,,,,, ,.00600 .00200 .0200 .0260 .496 .402 .0300 .0100 .00200 .00600

Группированная статистическая функция распределения

> F:=x->sum(p[i]*Heaviside(x-xr[i]),i=1..k):

> plot([F,f],Y[1]..Y[n],0..1,labels=['Y','F']);

Оценка параметров закона распределения

Накопленные частоты

> Fg:=evalf(cumulativefrequency(xp),3);

g [], , , ,,,,,,.00600 .00800 .0280 .0540 .550 .952 .982 .992 .994 1.

Линеаризация

> yg:=evalf(map(y->tan((y-0.5)*Pi*(1-2*eps)),Fg)):

Оценка параметров методом наименьших квадратов

> fit[leastsquare[[y,z]]]([xs,yg]);

+ 3.495959435 10.72620093

Пример 2.2 (Mathematica)

<<Calculus`DiracDelta`

<<Graphics`Graphics`; <<Graphics`Colors`

<<Statistics`ContinuousDistributions`

<<Statistics`DataManipulation`

x={10,10,10,30,20,12,10,12,20,10}; n=Length[x];

Y=Sort[x]; xm=Frequencies[Y]; X=Column[xm,2]

k=Length[X]; m=Column[xm,1]; p=N[m/n]

xp=Transpose[{N[Column[xm,1]/n],Column[xm,2]}]

f[y_]:=Sum[p[[i]]*UnitStep[y-X[[i]]],{i,k}];

Plot[f[y],{y,X[[1]]-1,X[[k]]+1}];

n=500; a0=0; a1=10; eps=0.01;

f[x_]:=ArcTan[a0+a1*x]/Pi+0.5; df=D[f[y],y];

g[z_]:=-( a0+Cot[Pi* z])/a1;

Y=RandomArray[UniformDistribution[0+eps,1-eps],n];

X=Map[g,Y]; Y=Sort[X];

k=10; R=Y[[n]]-Y[[1]]; h=R/k

xr=Table[Y[[1]]+i*h,{i,0,k}]

xs=Table[Y[[1]]+(i-1/2)*h,{i,k}]

m=BinCounts[Y,{Y[[1]],Y[[n]],h}]; m[[1]]+=1; m

p=N[m/n]

p1=BarChart[Transpose[{p,xs}],BarStyle->{Blue}];

p2=Plot[df,{y,Y[[1]],Y[[n]]},PlotStyle->{Red}];

pic1=Show[{p1,p2}];

F[y_]:=Sum[p[[i]]*UnitStep[y-xr[[i]]],{i,k}];

Plot[{F[y],f[y]},{y,Y[[1]],Y[[n]]},

PlotStyle->{Red,Green}];

Fg=CumulativeSums[p]

ygf[y_]:=Tan[(y-0.5)*Pi*(1-2*eps)]; yg=Map[ygf,Fg];

pXY=Transpose[{xs,yg}]; psi=Fit[pXY,{1,y},y]

Пример 2.3 (Matlab)

x=[10,10,10,30,20,12,10,12,20,10]; n=length(x);

Y=sort(x), X=[10,12,20,30], k=length(X);

m=[0,0,0,0];

for i=1:k, for j=1:n,

if Y(j)==X(i), m(i)=m(i)+1; end

end, end

m, p=m/n, f=cumsum(p), stairs(X,f)

n=500; a0=0; a1=10; eps=1e-2;

f=inline('atan(a0+a1*x)/pi+0.5','x','a0','a1');

df=inline('a1./((1+(a0+a1*x).^2)*pi)',...

'x','a0','a1');

g=inline('-(cot(pi*x)+a0)/a1','x','a0','a1');

Y=unifrnd(0+eps,1-eps,1,n); X=g(Y,a0,a1);

Y=sort(X); k=10; R=Y(n)-Y(1), h=R/k, i=0:k-1;

xr=Y(1)+i*h, [m,xs]=hist(Y,k), p=m/n, F=p/h

bar(xs,F,'histc'), hold on

x1=Y(1):0.1:Y(n); y1=df(x1,a0,a1);

plot(x1,y1,'r'), hold off, pause

Fg=cumsum(p); stairs(xr,Fg), hold on

y2=f(x1,a0,a1); plot(x1,y2,'r'), hold off, pause

yg=tan((Fg-0.5)*pi*(1-2*eps)), c=polyfit(xs,yg,1)

Пример 2.4 (Mathcad)

x 10101030201210122010()

n length x():=

Y sort x():=

10 10 10 10 10 12 12 20 20 30

X 10122030()

k length X():=

i0k1

−

.:=

j0n1−

.:=

if x

1, 0,

(

)

∑

5221()=

Fx()

Φ xX

−

(

)

⋅

∑

10 12 20 30()=

10 20 30

0.5

Fy()

0.5 0.2 0.2 0.1()=

n50

j0n1

−

.:=

ε 10

−

fx()

atan a

x⋅+

()

⋅

+:=

gx()

cot π x⋅

(

)

−:=

df x()

fx()

Y runif n 0 ε+, 1 ε−,

(

)

(

)

Y sort X():=

n1−

−

R 5.484

i0k1

−

.:=

h 0.548

i1+

+:=

−

+:=

i1+

m hist xr Y

():=

5 5 5 9 59 391 16 4 2 4

j1k1

−

..:=

j1−

202

df y()

202

0.5

fy()

-2.66 -2.11 -1.56 -1.01 -0.46 0.09 0.63 1.18 1.73 2.28

0.01 0.02 0.03 0.05 0.17 0.95 0.98 0.99 0.99 1

g2 x( ) tan x 0.5−()π⋅ 12ε⋅−

()

⋅

⎡

⎣

⎤

⎦

g2 Fg

(

)

F1 x() 1 x()

c linfit xs yg, F1,():=

1.753 9.944()=

Задание

1. Изучив теоретическое введение и примеры 2.1-2.4, разработать

собственный документ , решающий следующие задачи :

• получение выборки случайных чисел заданного объема с

заданным законом распределения (2.8) с помощью метода

обратных функций для заданный преподавателем значений пара-

метров закона распределения

a и

a ;

• получение вариационного ряда для негруппированной выборки;

• вычисление размаха выборки;

• группировка выборки;

• построение статистической функции распределения

(

)

x для

группированной выборки с разным количеством разрядов;

• оценка плотности распределения для группированной выборки.

Результатом работы документа должны быть массивы, содержащие

значения группированной статистической функции распределения

и значения середин разрядов. Эти данные являются исходными для

оценки параметров функции распределения по методу наименьших

квадратов (подобно тому, как это делалось в работе 1).

3. Аппроксимировать группированную статистическую функцию

распределения известной функцией (2.8), используя ранее

разработанный документ из работы 1 для решения задачи аппрок-

симации методом наименьших квадратов с линеаризацией.

Формулы для линеаризации зависимости (2.8)

вывести

самостоятельно.

4. Вычисления повторить для разных объемов исходной выборки -

N=100, 500 и 1000. Исследовать влияние количества разрядов груп-

пировки на получаемые значения параметров функции

распределения для объема выборки 1000.

Сравнить полученные по методу наименьших квадратов значения

оценок параметров

с заданными преподавателем и сделать

выводы о правильности проделанной работы.

Контрольные вопросы

1. Дайте определение генеральной совокупности, выборки, размаха

выборки и объема выборки.

Что мы называем вариационным и статистическим рядом, функци-

ей распределения и статистической функцией распределения?

Какими свойствами обладает статистическая функция распределе-

ния?

Дайте определение группированного статистического ряда. Как

строится гистограмма?

Дать определение сходимости по вероятности.

Что такое гамма-функция?

Записать формулы плотности распределения для нормального,

и распределения Стьюдента.

Для каждой из приведённых ниже выборок определить размах, а

также построить вариационный и статистический ряды

(Задачи № 1.1-1.3 гл.15 [2]).

3, 8, 1, 3, 6, 5, 2, 2, 7.

11, 15, 12, 0, 16, 19, 6, 11, 12, 13, 16, 8, 9, 14, 5, 11, 3.

10.

17, 18, 16, 16, 17, 18, 19, 17, 15, 17, 19, 18, 16, 16, 18, 18.

11.

Решить задачи №1.4–1.15, гл. 15[2].

3. Equation Section (Next)Точечная оценка числовых

характеристик.

Методы оценок параметров

Наиболее часто применяемыми числовыми характеристиками слу-

чайной величины

являются начальные и центральные моменты раз-

личного порядка. Для дискретной случайной величины моменты поряд-

ка

k определяются следующими формулами:

kii

∑

()

ki i

=−

∑

, (3.1)

для непрерывной случайной величины

()

fxdx

∞

−∞

∫

()

mfxdx

∞

−∞

=−

∫

Чаще всего используется первый начальный момент

, назы-

ваемый

математическим ожиданием случайной величины

, и второй

центральный момент

= , называемый дисперсией. Матожидание –

это среднее значение случайной величины, его называют еще центром

распределения, дисперсия характеризует разброс случайной величины

относительно центра распределения. Часто вместо дисперсии исполь-

зуют среднее квадратичное отклонение

Если закон распределения случайной величины неизвестен, то мы

не сможем вычислить числовые характеристики. В этом случае их за-

меняют оценками, полученными как функции выборки

()

, ,...,

xx x= . Всякую функцию

(

)

tx от выборки называют стати-

стикой. Подходящую статистику используют в качестве оценки число-

вой характеристики. Чаще всего оценками начальных и центральных

моментов служат соответствующие выборочные начальные и централь-

ные моменты

∑

()

mxMx

=−

∑

. (3.2)

Таким образом, оценкой математического ожидания служит выбо-

рочное среднее

∑

, но в качестве оценки можно взять и, на-

пример, величину

()

max min

0,5 xx⋅+ и другие величины.

Чтобы иметь практическую ценность, оценка некоторого параметра

должна удовлетворять следующим требованиям:

Оценка

(

)

tx должна приближаться к оцениваемому параметру

по мере увеличения объема выборки. Если оценка стремится по ве-

роятности к оцениваемому параметру, то она называется состоя-

тельной.

Оценка не должна содержать систематической ошибки. Это означа-

ет, что ее математическое ожидание должно совпадать с оценивае-

мым параметром

, т.е.

(

)

Mt x

⎡⎤

⎣⎦

. Такая оценка называется

несмещенной.

Из всех состоятельных и несмещенных оценок предпочтительнее

та, которая имеет наименьшую дисперсию. Такая оценка называет-

ся эффективной.

Например, среднее выборочное

x является состоятельной оцен-

кой математического ожидания, а

(

)

max min

0,5 xx⋅+ – несостоятельной.

Второй выборочный центральный момент

()

mS xMx

== −

∑

(3.3)

является состоятельной оценкой дисперсии, но эта оценка смещенная.

Несмещенными являются оценки

()

SxMx

=−

−

∑

()

Sxm

∗

=−

−

∑

. (3.4)

Если случайная величина распределена по нормальному закону, то

оценка

S является и эффективной.

Пусть закон распределения известен, но зависит от одного или не-

скольких неизвестных параметров. Например,

(

)

– известная плот-

ность распределения, а

(

)

,,..,

θθ

= – неизвестный параметр.

Требуется по выборке

(

)

, ,..,

xx x= оценить параметр

Существует несколько методов оценки параметра

. Мы рассмот-

рим два из них – метод моментов и метод функции правдоподобия.

Метод моментов заключается в том, что теоретический момент

го порядка

(

)

αθ

приравнивают к соответствующему

выборочному моменту

. Из полученного уравнения

(

)

θα

на-

ходят неизвестный параметр

. Например, случайная величина

(время безотказной работы радиоаппаратуры) распределена по экспо-

ненциальному закону

()

−

, 0t ≥ , (3.5)

где

T – неизвестный параметр. Оценим его по методу моментов. Для

этого найдем первый начальный момент

()

tf t dt te dt

∞∞

−

−∞

== =Τ

∫∫

Так как первый выборочный момент равен

x , то из равенства

= получим TMx

. Таким образом, оценкой неизвестного пара-

метра

, найденной по методу моментов, является среднее выборочное

x .

Пусть

(

)

,Lu

– плотность распределения выборочного вектора

()

,,..,

xx x= ,

(

)

,,..,

θθ

= – неизвестный параметр.

(

)

,Lu

–

функция двух аргументов, неслучайного

и случайного

()

,,..,

xx x= , называется функцией правдоподобия. Так как

(

)

,Lu

– плотность распределения, то оценка параметра

, доставляющая мак-

симум функции правдоподобия, является наиболее вероятной. Отсюда

(

)

∂θ

= или

()

ln , 0Lx

∂

∂θ

⎡⎤

⎣⎦

(3.6)

есть необходимые условия существования максимума. Оценка, полу-

ченная из условий (3.6), называется оценкой наибольшего правдоподо-

бия.

Пусть

(

)

, ,..,

xx x= – случайная выборка из генеральной сово-

купности, распределенной по нормальному закону

()

fx e

πσ

−

= , (3.7)

где

()

μσ

= – неизвестный параметр. Запишем функцию правдопо-

добия. Так как

– независимые случайные величины, распределенные

по тому же закону, а плотность распределения вектора равна произве-

дению плотностей составляющих вектора, то функция правдоподобия

будет следующей:

() ( ) ()

,, exp

(2 )

Lx f x x

θθ μ

πσ

⎡

⎤

== −−

⎢

⎥

⎣

⎦

∑

∏

. (3.8)

Пусть

– дискретная случайная величина, закон распределения

которой зависит от неизвестного параметра

(

)

(

)

pxp

. Будем

рассматривать выборку

()

, ,..,

xx x= как реализацию того, что слу-

чайная величина приняла последовательно значения

,,..,

xx. Веро-

ятность этого равна произведению вероятностей. Следовательно, функ-

ция правдоподобия будет

() ( )

Lx Px

∏

. (3.9)

Например, для дискретной случайной величины, распределенной по

закону Пуассона

()

pp k e

−

=== , 0,1, 2,3,...k

(3.10)

функция правдоподобия согласно (3.9) может быть записана в виде

()

Lx x e

μμ

−

⎛⎞

⎜⎟

⎝⎠

∑

∏

. (3.11)

Здесь

– целые неотрицательные числа. Однако при больших n

вычисления по формуле (3.11) могут приводить к переполнениям

разрядной сетки.

Получение оценок параметров иллюстрируется примерами 3.1-3.4.

В данных примерах создается выборка случайных чисел с

нормальным законом распределения при заданных параметрах

По полученной выборке вычисляются первый начальный момент и

второй центральный момент, которые могут служить состоятельными

несмещенными оценками математического ожидания и дисперсии

случайной величины.

Следующий раздел примеров показывает, как оценки этих

параметров могут быть получены по методу максимального

правдоподобия. Для этого вводятся функции правдоподобия и

определяются их экстремумы. В примере приводятся

графики функций

правдоподобия.

В примере также иллюстрируется использования метода

наибольшего правдоподобия к оценке параметров дискретной

случайной величины, распределенной по закону Пуассона. Находятся

оценки параметра

по методу моментов и по методу максимального

правдоподобия.

Пример 3.1 (Maple)

Часть 1. Оценка параметров нормального закона распределения

> restart: with(stats): randomize():

Объём выборки

> n:=50:

Заданные параметры нормального закона

> mu:=-1: sigma:=2:

Выборка с нормальным распределением

> x:=[random[normald[mu,sigma]](n)]:

Вычисление моментов

1-й начальный момент (оценка математического ожидания)

> m1:=1/n*sum(x[i],i=1..n);

:= m1 -1.28896380

2-й центральный момент (оценка дисперсии)

> m2:=1/(n-1)*sum((x[i]-m1)^2,i=1..n);

:= m2 3.48637842

оценка ср. кв. отклонения

> s:=sqrt(m2);

1.86718462

Оценка параметров

нормального распределения

Плотность нормального распределения

> f:=(x,mu,sigma)->exp(-(x-mu)^2/2/sigma^2)/

sqrt(2*Pi*sigma^2);

:= f → (),,x μσ

⎛

⎝

⎜

⎞

⎠

⎟

− /12

() − x μ

2 πσ

Функция правдоподобия

> L:=(mu,sigma)->product(f(x[i],mu,sigma),i=1..n);

:= L → (),μσ

∏

= i 1

()f,,x

μσ

Поиск наиболее правдоподобных значений параметров

> sys:={sigma1>0, diff(ln(L(mu1,sigma1)),mu1)=0,

diff(ln(L(mu1,sigma1)),sigma1)=0}:

> M:=solve(sys,{mu1,sigma1});

{}, =

1 1.848418476

= μ1 -1.288963807

Наиболее правдоподобные значения параметров

> m:=subs(M,[mu1,sigma1]);

:= m [],-1.288963807 1.848418476

Другой способ вычисления

> M:=maximize(L(mu1,sigma1),mu1=-infinity..

infinity,sigma1=0..infinity, location)[2];

:= M {}

⎡

⎣

⎢

⎤

⎦

⎥

,[], = σ1 1.848418476 = μ1 -1.288963807 .189179040810

-31

> m:=subs((op@op)(M)[1],[mu1,sigma1]);

:= m [],-1.288963807 1.848418476

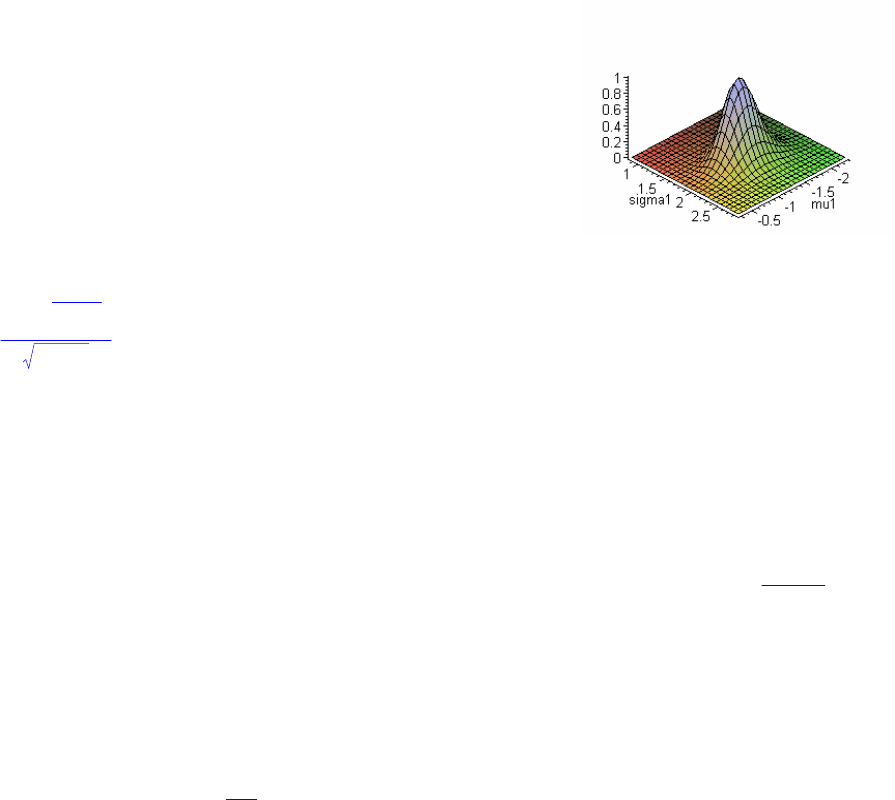
График функции правдоподобия

> plot3d(L(mu1,sigma1)/L(m[1],m[2]),mu1=m[1]-1..

m[1]+1,sigma1=m[2]-1..m[2]+1,axes=FRAME);

Часть2. Исследование параметров выборки с распределением Пуассона

Объём выборки

> n:=20:

Заданный параметр распределения Пуассона

> mu:=5:

Выборка с распределением Пуассона

> x:=evalf([random[poisson[mu]](n)]);

[],,,,,,,,,,,,,,,,,,,4. 5. 4. 2. 8. 5. 4. 3. 5. 6. 1. 4. 6. 5. 3. 6. 7. 7. 6. 4.

1-й начальный момент

> m1:=1/n*sum(x[i],i=1..n);

:= m1 4.75000000

Плотность распределения Пуассона

> p:=(x,mu)->exp(-mu)*mu^x/x!;

:= p → (),x μ

()

−

Функция правдоподобия

> L:=(mu)->product(p(x[i],mu),i=1..n);

:= L → μ

∏

= i 1

()p,x

Наиболее правдоподобное значение параметра

> m:=solve(diff(ln(L(mu1)),mu1)=0,mu1);

:= m 4.75000000

Другой способ вычисления

> M:=maximize(evalf(L(mu1)),

mu1=0..infinity,location)[2];

:= M {}[],{} =

1 4.750000000 .325905629410

-17

> m:=subs((op@op)(M)[1],mu1);

:= m 4.75000000

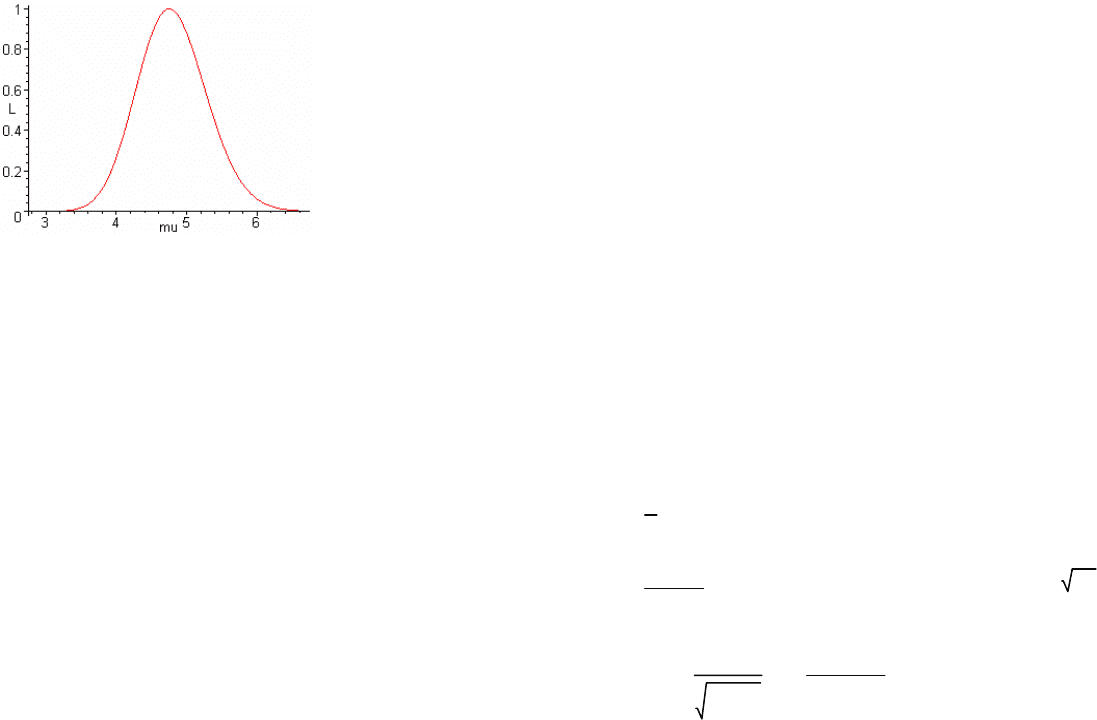
График функции правдоподобия

> plot(L(mu1)/L(m),mu1=m-2..m+2,labels=['mu','L']);

Пример 3.2 (Matematica)

<<Statistics`ContinuousDistributions`

<<Statistics`DiscreteDistributions`

n=50; mu=-1; sigma=2;

x=RandomArray[NormalDistribution[mu,sigma],n];

m1=1/n*Apply[Plus,x]

m2=1/n*Apply[Plus,(x-m1)^2]

s=Sqrt[m2]

f[x_,mu_,sigma_]:=Exp[-(x-mu)^2/2/sigma^2]/

Sqrt[2*Pi*sigma^2];

L[mu_,sigma_]:=Apply[Times,f[x,mu,sigma]];

M=FindMinimum[-L[mu1,sigma1],{mu1,0},{sigma1, 1}]

m={mu1,sigma1}/.M[[2]]

Plot3D[L[mu1,sigma1]/L[m[[1]],m[[2]]],{mu1,

m[[1]]-1,m[[1]]+1},{sigma1, m[[2]]-1,m[[2]]+1},

AxesLabel->{"mu","sigma","L"}];

n=20; mu=5;

x=N[RandomArray[PoissonDistribution[mu],n]];

m1=1/n*Apply[Plus,x]

p[x_,mu_]:=Exp[-mu]*mu^x/x!;

L[mu_]:=Apply[Times,p[x,mu]];

M=FindMinimum[-L[mu1],{mu1,1}]

m=mu1/.M[[2]]

Plot[L[mu1]/L[m],{mu1,m-2,m+2}];

Пример 3.3 (Matlab)

n=50; mu=-1; sigma=2; x=normrnd(mu,sigma,1,n);

m1=1/n*sum(x)

m2=1/(n-1)*sum((x-m1).^2), s=sqrt(m2)

f=inline(...

'exp(-(x-mu).^2/2/sigma^2)/sqrt(2*pi*sigma^2)',...

'x','mu','sigma');

L=inline('-prod(feval(f,x,theta(1),theta(2)))',...

'theta','f','x');

m=fminsearch(L,[0,1],[],f,x)

mu1=m(1)-1:0.1:m(1)+1; sigma1=m(2)-1:0.1:m(2)+1;

for i=1:length(mu1), for j=1:length(sigma1)

L1(i,j)=L([mu1(i),sigma1(j)],f,x);

end, end

L1=L1/L(m,f,x); surfl(mu1,sigma1,L1), pause

n=20; mu=5; x=poissrnd(mu,1,n);

m1=1/n*sum(x)

p=inline('exp(-mu)*mu.^x/factorial(x(1))',...

'x','mu');

L=inline('-prod(feval(p,x,theta))',...

'theta','p','x');

m=fminsearch(L,[1],[],p,x)

mu2=m-2:0.1:m+2;

for i=1:length(mu2), L2(i)=L(mu2(i),p,x); end

L2=L2/L(m,p,x); plot(mu2,L2)

Пример 3.4 (Mathcad)

i0n1

−

.:=

μ 1−:=

x rnorm n μ,σ,

(

)

∑

⋅:=

m1 1.081

−

n1−()

m1−

()

∑

⋅:=

m2 3.269

s 1.808

fxμ,σ,

()

2 π⋅σ

⋅

exp

x μ−

()

−

2 σ

⋅

⎡

⎢

⎣

⎤

⎥

⎦

⋅:=

L μσ,

(

)

μ,σ,

(

)

∏

μ1

σ11:=

Give

σ1

μ1

ln L μ1 σ1,

()()

σ1

ln L μ1 σ1,

()()

m Find μ1 σ1,

()

1.081− 1.79()=

i02

..:=

j02

.:=

ij,

−

0.1 i

⋅

−

0.1 j

⋅

(

)

()

i0n1−

.:=

x rpois n μ,

(

)

∑

⋅:=

m1 4

pxμ,

()

μ−

⋅:=

L μ

()

μ,

(

)

∏

⎛

⎜

⎝

⎞

⎟

⎠

⋅:=

μ11:=

m root

μ1

ln L μ1

()()

μ1,

⎛

⎜

⎝

⎞

⎟

⎠

0.5

L μ2()

Lm()

μ2

Задание

Изучив теоретическое введение и примеры, разработать

собственный документ, решающий следующие задачи:

получение выборки случайных чисел заданного объема с

нормальным законом распределения

(

)

(непрерывная

случайная величина);

получение оценок параметров

по методу моментов;

получение оценки параметров

по методу максимального

правдоподобия;

получение выборки случайных чисел заданного объема с

распределением по закону Пуассона с заданным параметром

(дискретная случайная величина);

получение оценок параметра

закона Пуассона по методу

максимального правдоподобия и по методу моментов.

Расчитать по двум документам для объемов выборок 10, 50 и 100.

Сравнить полученные результаты с теоретическими и сделать

выводы о правильности проделанной работы.

Записать функцию правдоподобия для закона Коши:

()

⎛⎞

⎜⎟

+−

⎝⎠

Можно ли оценить параметр

по методу наибольшего правдопо-

добия?

Контрольные вопросы

1. Назовите выборочные числовые характеристики.

Что такое статистики и для чего они служат?

Какими свойствами должны обладать оценки?

Приведите примеры состоятельной, несмещенной и эффективной

оценок.

Что такое функция правдоподобия? В чем сущность метода

наибольшего правдоподобия ?

Пусть

,,,

XXK – выборка из генеральной совокупности с из-

вестным средним m и неизвестной дисперсией

. Показать, что

несмещённой оценкой для

будет статистика

()

SXm

=−

∑

(Задача № 2.13 гл.15 [2]).

Решить задачи № 2.14, 2.21, 2.32-2.35 гл. 15 [2].

4. Equation Section (Next)Интервальные оценки

числовых характеристик

В предыдущей работе были рассмотрены методы, дающие оценку

параметра в виде некоторого числа или точки на числовой оси. Такие

оценки называют точечными. Точечная оценка без указания степени

точности и надежности не имеет практического значения, так как пред-

ставляет собой только возможное значение случайной величины, т.е.

сама точечная оценка является величиной

случайной. Можно доказать,

что в выборке объема n из генеральной совокупности, распределенной

по нормальному закону

()

,Na

среднее выборочное

x распределено

также по нормальному закону

()

,Na n

. Величина

/nS

∗

распре-

делена по закону

с n степенями свободы, а

(

)

tMxanS=− − –

по закону Стьюдента с

1n − степенью свободы.

Чтобы получить представление о точности и надежности оценки

для параметра

, возьмем достаточно большую вероятность

и най-

дем такое

> , для которого

()

θδ

−< =

или

(

)

(

)

θθ δ θδ θ δθ

−

<−< = −<<+ =

%% %

. (4.1)

Равенство (4.1) означает, что точное, но неизвестное значение па-

раметра

с вероятностью

накрывается интервалом

()

δθ δ

=− +

. Этот интервал называют доверительным, а вероят-

ность

– доверительной вероятностью или надежностью оценки. Оче-

видно, чем меньше

для заданного

, тем точнее оценка.

В общем случае интервал, образованный статистиками

(

)

Ux и

()

Vx, называется доверительным для оцениваемого параметра

, если

выполняется равенство

() ()

()

PU x V x

θβ

<< = . (4.2)

Здесь

– выборочный вектор, надежность

выбирается близкой

к единице. Концы интервала называются доверительными границами.

Порядок нахождения доверительного интервала следующий. По-

дыскивают подходящую статистику

(

)

, зависящую от параметра

, но распределение которой от этого параметра не зависит. Задают

надежность

, и по закону распределения статистики

(

)

находят

доверительные границы из условия (4.2). Затем полученное неравенство

решают относительно

Рассмотрим нахождение доверительного интервала на примерах.

Пример 1. Найдем доверительный интервал для математического

ожидания

по заданной выборке

(

)

,,...,

xx x= из генеральной

совокупности, распределенной по нормальному закону

(

)

,Na

считая, что

x и

S – точечные оценки математического ожидания и

дисперсии.

Рассмотрим статистику

(

)

(

)

txa Mxa n S=− −. Как отмечалось

выше, она распределена по закону Стьюдента с

−

степенью свобо-

ды. Тогда

() ()

2fxdx fxdx

δδ

−

∫∫

. (4.3)

В формуле (4.3) плотность

(

)

x определяется выражением (2.6), в

которое вместо

n следует поставить 1n

−

. Неизвестное

определяет-

ся из (4.3), а доверительный интервал – из неравенства

()

1Mx a n S

−−<.

Таким образом,

lMx Mx

δδ

⎛⎞

=− +

⎜⎟

−

⎝⎠

. (4.4)

Пример 2. В условии примера 1 найдем доверительный интервал

для дисперсии

Для этого выберем статистику

()

= . Согласно сказанно-

му выше она распределена по закону

с 1n

−

степенью свободы. Оп-

ределение доверительного интервала аналогично, но осложняется не-

симметричностью закона распределения

. Действительно, уравнение

()

fxdx

∫

(4.5)

имеет неоднозначное решение относительно

t и

t . Здесь плотность

()

x определяется формулой (2.5), только n следует заменить на

−

. Ради однозначности наложим дополнительные условия, а именно

будем считать, что

() ()

xdx f xdx

∞

−∞

∫∫

. (4.6)