Филатов Е.Ю., Ясинский Ф.Н. Математическое моделирование течений жидкостей и газов
Подождите немного. Документ загружается.


движении жидкости в сосуде. В задаче имеются все
перечисленные виды границ: твердая стенка (верхняя и нижняя
границы), входная (левая) и выходная (правая) границы.
Рассмотрим, как граничные и начальные условия
используют для нахождения поля скоростей.
На твердой стенке скорость (обе ее проекции) должна
быть равна 0: здесь используется граничное условие I рода.
В приточном отверстии обычно также используют
граничное условие I рода: проекцию скорости вдоль границы U
y
(рис. 1) берут равной 0, а проекцию скорости по нормали к
границе U
x
рассчитывают исходя из параболического профиля
(рис. 1). Таким образом, вблизи стенок проекция скорости U
x
уменьшается до 0, а в середине отверстия она достигает
максимального значения U
max
. Параболический профиль можно
рассчитать, например (в случае, если приточное отверстие
располагается вдоль всей левой границы) по формуле
.
2
1
1
2
,0
max
y
y
j
x
U
N
jjN
U
(7.1)
Для вытяжного отверстия можно использовать различные
граничные условия. Если есть уверенность, что профиль
исходящего потока будет также параболическим (как в
приведенном примере), то можно задать граничное условие I
рода с этим профилем. Важно правильно рассчитать U
max
для
этого отверстия, если приточных отверстий несколько или
приточное и вытяжное отверстия разных размеров. Для
вытяжного отверстия, для проекции скорости по нормали к
границе U
x
можно также использовать граничное условие II рода,
при котором производная (по нормали к границе) скорости U
x
равна 0. Разностная схема при этом имеет вид
.
,,1 jN
x
jN
x
xx
UU
(7.2)
Иногда также используют такое граничное условие, при
котором вторая производная (по нормали к границе) скорости U
x
равна 0.
21

.2
,1,,1 jN
x
jN
x
jN
x
xxx
UUU
(7.3)
В качестве начального значения для поля скоростей можно
взять нулевое значение на всей рассматриваемой области. Однако
представляется, что стационарное решение будет найдено скорее,
если в качестве начального значения для поля скоростей взять
значение, приближенное к результату.
Для поля давления (или поля плотности) обычно на всех
границах используют граничное условие II рода, то есть задается
производная давления (плотности) по нормали к границе.
Величину этой производной находят из уравнений Навье-Стокса
(2.1) и (2.2). Однако это требует дополнительных расчетов.
Поэтому в целях упрощения производную давления (плотности)
часто берут равной 0 на всех границах. На входных и выходных
границах используют также граничное условие, при котором не
первая, а вторая производная равна 0. Заметим, что поскольку
нигде на границе не используется граничное условие I рода, то
давление (плотность), не закрепленное ни в одном узле, может
плавать. Поэтому иногда давление (плотность) принудительно
закрепляют в каком-либо узле или в среднем по всей
рассматриваемой области.
Если расчет давления ведется с помощью уравнения
Пуассона, то представляется, что начальные условия для поля
давления не окажут особого влияния на результат: после первого
же шага по времени поле давления будет зависеть лишь от поля
скорости. Если же давление находится с помощью метода слабой
сжимаемости, то, наверное, выбор начальных значений, близких
к результату, будет более продуктивен. В любом случае самый
простой способ задания полей давления и плотности – это
задание их константами на всей рассматриваемой области.
Иногда используют такие граничные условия. В
приточном и вытяжном отверстиях давление задают разными
константами, а для скорости берут граничное условие II рода, при
котором производная скорости равна 0. Таким образом, движение
жидкости происходит из-за разности давлений на входе и выходе,
22

будучи ограничено при этом влиянием силы трения о твердые
стенки.
8. Уравнения гидродинамики в системе
«вихрь – функция тока»
В разделах 1–7 мы решали задачи гидродинамики в
системе «давление – скорость». В данном разделе будет
рассмотрена система «вихрь – функция тока». Она устойчивее,
быстрее и удобнее, чем система «давление – скорость».
Определим прежде такие физические величины, как функция
тока ψ и вихрь ω.
Перепишем уравнения Навье-Стокса:
;
1
2
2
2
2
x
xxx
y
x
x
x
F
x
P
y
U
x
U
y
U
U
x
U
U
t
U
(8.1)
.
1
2
2
2
2
y
yyy
y
y
x
y
F
y
P
y
U
x
U
y
U
U
x
U
U
t
U
(8.2)
Определим вихрь
.
y
U
x
U
x
y
(8.3)
Продифференцируем уравнение (8.1) по y, а уравнение
(8.2) по x и вычтем одно из другого. Учитывая уравнение
неразрывности, получим:
,
2
2
2
2
yxy
U
x
U
t
yx
(8.4)
где
.
y
F
x
F
x
y
(8.5)
23

Уравнение (8.4) носит название уравнения Гельмгольца.
Для того чтобы система была полной, требуются дополнительные
уравнения. Определим функцию тока ψ так, чтобы
.;
x
U
y
U
yx
(8.6)
Такая функция ψ существует, это следует из уравнения
неразрывности. Если мы подставим эти формулы (8.6) в
определение вихря (8.3), то получим уравнение Пуассона:
.
2
2
2
2
yx
(8.7)
Уравнение (8.7), уравнение Гельмгольца (8.4),
определение функции тока (8.6) и начальные и граничные
условия образуют полную систему.
Расчет полей выполняется по следующему алгоритму.
Изначально известны поля функции тока ψ и вихря ω. Из
определения функции тока (8.6) находится поле скоростей
U
.
Затем решается уравнение Гельмгольца (8.4) и находится новое
значение поля вихря ω. И, наконец, из уравнения Пуассона (8.7)
находится новое значение поля функции тока ψ. Далее алгоритм
повторяется.
Уравнение Пуассона и уравнение Гельмгольца решаются
методами, изложенными выше (разделы 3, 5, 6). Для нахождения
поля скоростей используют следующую разностную схему:
.
4
1,11,11,11,1
,
h
U
jijijiji
ji
x
(8.8)
Схема для U
y
строится аналогично.
9. Граничные и начальные условия
в системе «вихрь – функция тока»
Для решения задачи в системе «вихрь – функция тока»
осталось лишь задать граничные и начальные условия. В этой
24

системе имеется большое разнообразие граничных условий.
Приведем лишь некоторые из них.
Для функции тока на твердой стенке, входной и иногда
выходной границах используют граничное условие I рода.
Значения функции тока рассчитываются исходя из профилей
скорости в приточных отверстиях по формулам (8.6). Вдоль
каждой твердой стенки значение функции тока постоянно. На
выходной границе также используют граничное условие II рода,
при котором производная функции тока равна 0.
Для примера рассчитаем значения функции тока на
границах для задачи, показанной на рис. 1. Узлом с координатами
(0,0) будем считать узел, расположенный сверху слева. Для
верхней стенки зададим
.0
0,
i
На левой границе ψ будем
рассчитывать следующим образом:
.
0
,0
,0
j
l
l
xj
Uh
(9.1)
На нижней стенке зададим
maxNNi
yy
1,01,
.
На правой границе поставим граничное условие II рода:
.
,,1 jNjN
xx
(9.2)
В качестве начального условия распределение функции
тока лучше задавать близкой к результату. Например, для
рассматриваемого примера можно задать:
.
,0, jji
Найдем теперь граничные условия для вихря.
Рассмотрим горизонтальную твердую стенку j=0. Так как
нормальная составляющая скорости U
y
в пограничном слое вдоль
этой стенки можно считать равной 0, то из определения вихря
(8.3) и определения функции тока (8.6) следует
.
2
2
yy
U
x
(9.3)
Для этого выражения можно записать следующую
разностную схему, используя фиктивный член ψ
i,–1
:
.
2
2
1,0,1,
0,
h
iii
i
(9.4)
25

Так как на твердой стенке
0
x
U
, то, учитывая
определение функции тока (8.6), можно записать
1,0,
ii
,
следовательно:
.
2
1,0,
0,
h
ii
i
(9.5)
Это и есть граничное условие для вихря ω на твердой
стенке.
На входной и выходной (если для функции тока задано
граничное условие I рода) границах для вихря можно поставить
либо граничное условие I рода:
2
1,0,01,0
2
,1,0
,0
2
hh
jjjjj
j
(9.6)
(оно выводится аналогично граничному условию на твердой
стенке), либо граничное условие II рода, при котором
производная вихря равна 0:
.
,1,0 jj
(9.7)
Для выходной границы, если для функции тока на ней
задано граничное условие II рода, следует поставить граничное
условие II рода, при котором производная вихря равна 0
(аналогично (9.7)).
В качестве начального условия для вихря, его можно
задать равным 0 на всей рассматриваемой области.
10. Расчет нагрузки
при гидродинамических процессах
Для того чтобы рассчитать силу, с которой среда
действует на помещенное в нее твердое тело, необходимо знать
распределение давления в этой среде. В системе «давление –
скорость» поле давления находится автоматически. Чтобы найти
26
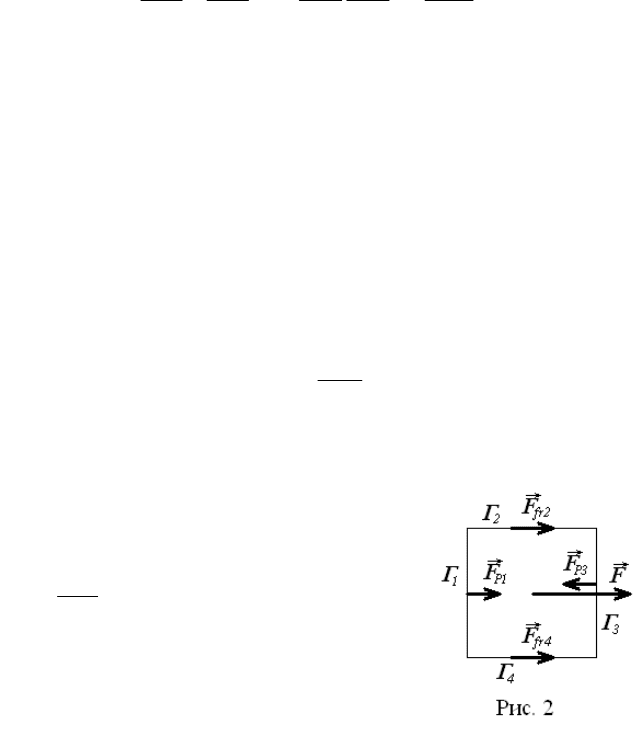
поле давления в системе «вихрь – функция тока», необходимо
решить уравнение Пуассона
.2
2
2
2
2
2
2
2
2
2
2
yxyxy
P
x
P
P
(10.1)
Силу, действующую на тело, находят как векторную
сумму двух составляющих – силы давления среды на тело и силы
трения среды о тело:
.
frP
FFF
(10.2)
Сила давления вычисляется как интеграл давления по
поверхности тела:
,
S
P
dsnPF
(10.3)
где S – поверхность тела, а
n
– вектор нормали к элементарной
поверхности ds, направленный от тела.
Сила трения вычисляется по следующей формуле:
,
S
s
fr
ds
n
U
F
(10.4)
где
s
U
– проекция вектора скорости на плоскость, параллельную
элементарной поверхности ds.
Для примера рассмотрим задачу в
двумерном случае. Здесь уже будем
вычислять не силу
F
, а силу на единицу
длины
z
F
. Пусть поток жидкости
движется слева направо и обтекает тело
прямоугольной формы (рис. 2). Положим
также, что движение симметрично
относительно оси симметрии тела,
параллельной оси Ox. Тогда силу давления
нужно вычислять только на границах Г
1
и Г
3
, а силу трения –
только на одной из границ Г
2
или Г
4
(на этих границах сила
трения одинакова). В результате расчет ведется по формулам:
27
;
;0;
31
PdyPdy
z
F
z
F
z
F
z
F
z
F
P
yfr
P
x
.2
2
dx
y
U
z
F
x
fr
(10.5)
11. О моделировании турбулентных
течений
Как ламинарные, так и турбулентные течения можно
описать уравнениями
;3,2,1;
1
3
1
3
1
i
x
P
x
S
x
U
U
t
U
j
ij
ij
j
i
j
j
i
(11.1)
;0
3
1
i
i
i
x
U
(11.2)
.
i
j
j
i
effij
x
U
x
U
S
(11.3)
Здесь U
i
– составляющие вектора скорости по
координатным осям x
i
соответственно; ν
eff
– эффективная
кинематическая вязкость. Она состоит из молекулярной ν
mol
и
турбулентной ν
turb
:
.
turbmoleff
(11.4)
Если турбулентная вязкость отсутствует или она может
быть принята постоянной в изучаемом объеме, то уравнение
(11.1) принимает вид Навье-Стокса:
.3,2,1;
1
3
1
2
2
3
1
i
x
P
x
U
x
U
U
t
U
i
j
j
i
eff
j
i
j
j
i
(11.5)
28
В противном случае сохраняется форма Рейнольдса (11.1).
Для вычисления турбулентной вязкости существует
множество моделей. Рассмотрим три из них.
Согласно модели Прандтля–Кармана турбулентная
вязкость вычисляется следующим образом:
.
2
Dl
turb
(11.6)
Здесь l – длина пути перемешивания. Это некоторый
аналог длины свободного пробега молекул между соударениями.
Только в данном случае обмен количеством движения
происходит не между отдельными молекулами, а между жидкими
макрочастицами при хаотических пульсациях скорости в
турбулентном потоке. D – величина, оценивающая интенсивность
деформации среды. Она вычисляется следующим образом:
.
2/1
,
i
j
j
i
ji
j
i
x
U
x
U
x
U
D
(11.7)
Вблизи неподвижной твердой стенки D принимает
следующий простой вид:
,
y
U
D
(11.8)
где U – величина скорости (параллельной стенке); y – нормаль к
стенке.
Т. Карман для вычисления l предложил выражение
,
2
2
y
U
y
U
l
(11.9)
где κ – так называемая постоянная Кармана. Эксперимент
показал, что κ = 0,36÷0,4. Можно легко убедиться, что вблизи
стенки выражение (11.9) принимает особенно простой вид:
.yl
(11.10)
В этом случае
.
22
y
U
y
turb
(11.11)
Вместо (11.9) для грубой оценки l подходит также
выражение
,
min
Ll
(11.12)
29

где L
min
– кратчайшее расстояние до ближайшей неподвижной
твердой поверхности.
Сполдингом предложена следующая формула для
вычисления в двумерном случае турбулентной вязкости:
.
2/1
2
1
2
2
2
1
2
x
U
x
U
l
turb
(11.13)
При всей своей простоте эта формула дает хорошие
результаты.
Существенным недостатком изложенной выше модели,
которую часто называют алгебраической, помимо невысокой
точности, является мгновенное изменение турбулентной вязкости
с изменением поля средних скоростей. Это, очевидно, не
соответствует действительности, т.к. реальное поле турбулентной
вязкости обладает определенной инерционностью и с изменением
поля скоростей
U
сложно изменяется со временем. Очевидно,
что поля ν
turb
и
U
взаимозависимы. Однако для установившихся
течений изложенная модель достаточно удобна и дает
приемлемую для инженерных расчетов точность.
Более совершенной является модель А.Н.Секундова. В
этой модели поле турбулентной вязкости описывается
дифференциальным уравнением
3
1
3
1 j
j
turb
turbmol
jj
turb
j
j
turb
xxx
U
t
.
8
2
turbturbmolmin
mol
turb
turb
LDf
(11.14)
Здесь f(∙) – следующая функция:
;
147,1
2,047,1
2,0
2
2
zz
zz
zf
(11.15)
κ, β, γ – эмпирические константы (κ = 2; β = 0,06; γ = 50).
На неподвижных твердых поверхностях Г ставится
граничное условие
0
Гturb
. Чтобы поле турбулентной вязкости
сформировалось, нужно задать некоторое его начальное
значение. В качестве такого можно принять значения,
30
