Филатов Е.Ю., Ясинский Ф.Н. Математическое моделирование течений жидкостей и газов



































h

DD

UU

h

DD

UU

h

DD

UU

h

DD

UU

k

ji

k

ji

k

ji

y

k

ji

y

k

ji

k

ji

k

ji

y

k

ji

y

k

ji

k

ji

k

ji

x

k

ji

x

k

ji

k

ji

k

ji

x

k

ji

x

1

,

1

1,

,,

1

1,

1

,

,,

1

,

1

,1

,,

1

,1

1

,

,,

22

















2

1

,

1

1,

1

1,

1

,1

1

,1

4

h

DDDDD

k

ji

k

ji

k

ji

k

ji

k

ji



.

22

1

1,

1

1,

1

,1

1

,1



















h

FF

h

FF

k

ji

y

k

ji

y

k

ji

x

k

ji

x

(2.10)

3. Решение уравнения Пуассона

Рассмотрим, как решается уравнение Пуассона:

.

2

A

y

P

x

P

P 









(3.1)

Запишем разностную схему для этого уравнения:

,

22

,

2

1,,1,

2

,1,,1

ji

jijijijijiji

A

h

PPP

h

PPP











(3.2)

или:

 

.

,

2

1,1,,1,1

4

1

, jijijijijiji

AhPPPPP 



(3.3)

Значение P

i,j

будем рассматривать как значение на новом

(l+1)-м шаге, а остальные значения P – как значения на старом l-м

шаге:

 

.

,

2

1,1,,1,1

4

1

, ji

l

ji

l

ji

l

ji

l

ji

l

ji

AhPPPPP 





(3.4)

Эти вычисления проводятся до тех пор, пока поле P не

станет «почти» стационарным. Условие завершения итераций

можно записать следующим образом:

,max

,

1

,





 l

ji

l

ji

PP

(3.5)

11

где



– допустимая погрешность.

Заметим, что для каждого шага по времени при решении

системы уравнений гидродинамики нужно использовать серию

итераций (3.4) в решении уравнения Пуассона. Не следует путать

шаги l в решении уравнения Пуассона с шагами по времени k в

решении системы уравнений гидродинамики.

Изложенный метод носит название метода Ричардсона.

При такой реализации требуется заводить временный массив для

нового (или старого) значения P и дополнительно (при

простейшей реализации) потребуется пересылать значения из

одного массива в другой. Однако можно обойтись и без

дополнительного массива. Для этого при сканировании сетки,

нужно сразу же заменять старое значение P новым:

 

.

,

21

1,1,

1

,1,1

4

1

, ji

l

ji

l

ji

l

ji

l

ji

l

ji

AhPPPPP 











(3.6)

Данный метод носит название метода Либмана. Он всегда

сходится, хотя иногда довольно медленно. Для ускорения

сходимости можно использовать метод верхней релаксации:

 

,

4

1

,

21

1,1,

1

,1,1,

1

, ji

l

ji

l

ji

l

ji

l

ji

l

ji

l

ji

AhPPPPPP 













(3.7)

где θ –некоторая константа. Практика показала, что если взять

85,1



, то вычисления сходятся достаточно быстро.

4. Метод слабой сжимаемости

для нахождения поля давления

Для нахождения поля давления из поля скорости

используют также метод слабой сжимаемости. Этот метод

предполагает, что рассматриваемая жидкость может немного

сжиматься. В таком случае уравнение неразрывности принимает

вид

12

 

.0div 



U

t



(4.1)

Часто вместо него используют уравнение

 

.div









U

t



(4.2)

Раскрыв знак дивергенции, получим уравнение,

напоминающее уравнение Навье-Стокса:

.divU

y

U

x

U

t

yx



















(4.3)

Оно решается теми же методами, что и уравнение Навье-

Стокса (см. разделы 5, 6).

Поле давления из поля плотности находится по формуле

,

n

P





(4.4)

где n – константа среды. Например, для воздуха n = 1,4.

Это уравнение можно переписать таким образом:

,

0

n

P





(4.5)

где P

0

и ρ

0

– средние давление и плотность среды в начальный

момент времени. Таким образом находится поле давления P.

Иногда применяют упрощенный вариант метода слабой

сжимаемости. В этом случае решается уравнение:

,div

2

Uc

t

P







(4.6)

где c – некоторая константа.

Метод слабой сжимаемости навязывает довольно малый

шаг по времени. В противном случае процесс может быть

неустойчивым. Для повышения устойчивости разностную схему

для дивергенции скорости записывают согласно формуле (2.6).

(В методе слабой сжимаемости, в отличие от решения

уравнения Пуассона, выполняется только одна итерация на

каждом шаге по времени.)

13

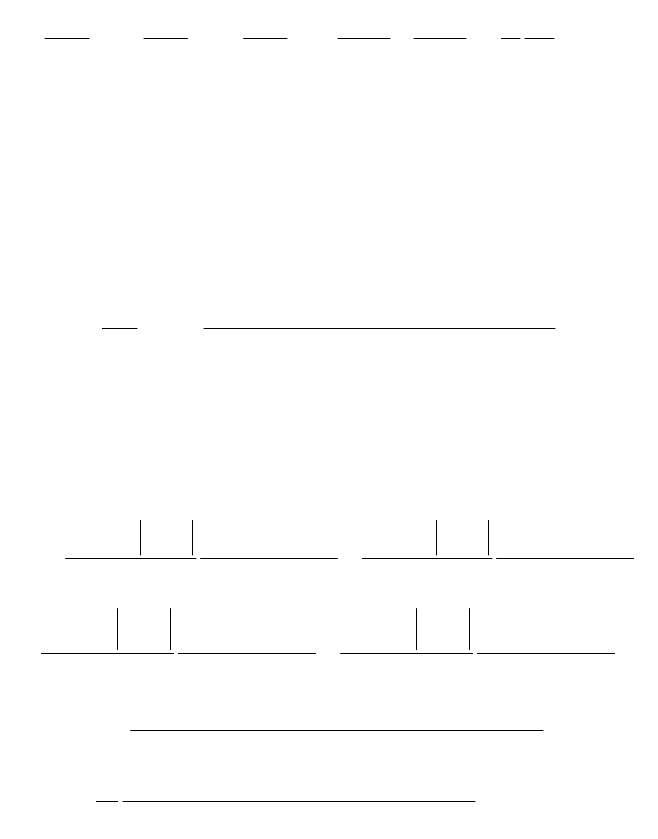
5. Решение уравнений Навье-Стокса:

явная схема

Перепишем уравнение Навье-Стокса при проекции на ось

Ox:

.

1

2

x

xxx

y

x

F

x

P

y

U

x

U

y

U

x

U

t

U









































(5.1)

Составим явную разностную схему к этому уравнению.

Явная разностная схема предполагает запись временной

производной искомого поля (U

x

) в k-й и (k+1)-й моменты

времени, а запись всех остальных членов с искомым полем (U

x

) в

k-й момент времени.

При составлении разностной схемы для повышения

устойчивости используют противоточные производные (2.8), а

для вычисления градиента давления применяют схему

.

4

1,11,11,11,1

,

h

PPPP

x

P

jijijiji

ji





















(5.2)

Для градиента давления по оси Oy строится аналогичная

схема.

Таким образом, явная разностная схема для уравнения

(5.1) имеет вид



















h

UU

h

UU

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

,,1

,,

,1,

,,

,

1

,

22













h

UU

h

UU

k

ji

x

k

ji

x

k

ji

y

k

ji

y

k

ji

x

k

ji

x

k

ji

y

k

ji

y

,1,

,,

1,,

,,

22









2

,1,1,,1,1

4

h

UUUUU

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x



.

4

1

,

1

1,1

1

1,1

1

1,1

1

1,1





























k

ji

x

k

ji

k

ji

k

ji

k

ji

F

h

PPPP



(5.3)

14

6. Решение уравнений Навье-Стокса:

неявная схема

Неявная разностная схема для решения уравнения Навье-

Стокса

x

xxx

y

x

F

x

P

y

U

x

U

y

U

x

U

t

U









































1

2

(6.1)

предполагает запись временной производной искомого поля (U

x

)

в k-й и (k+1)-й моменты времени, а запись всех остальных членов

с искомым полем (U

x

) – в (k+1)-й момент времени. Однако

решить такую разностную схему в двумерном и более случаях не

представляется возможным. Для одномерного случая такой

алгоритм существует. Он называется методом прогонки и будет

рассмотрен ниже. Для решения же уравнений Навье-Стокса в

двумерном и более случаях их сводят к одномерному случаю. В

этом и состоят методы переменных направлений и расщепления.

В методе переменных направлений шаг по времени

делится на 2 этапа продолжительностью τ/2. На первом этапе

строится разностная схема, неявная в направлении Ox и явная в

направлении Oy. На втором этапе наоборот, строится разностная

схема, явная в направлении Ox и неявная в направлении Oy. Для

первого этапа строится схема







































k

x

k

y

k

x

k

x

k

x

k

x

y

U

x

U

UU

2

1

2

1

2/



.

1

2

1



















































k

x

k

x

k

x

F

x

P

y

U

x

U





(6.2)

Для второго этапа:

15









































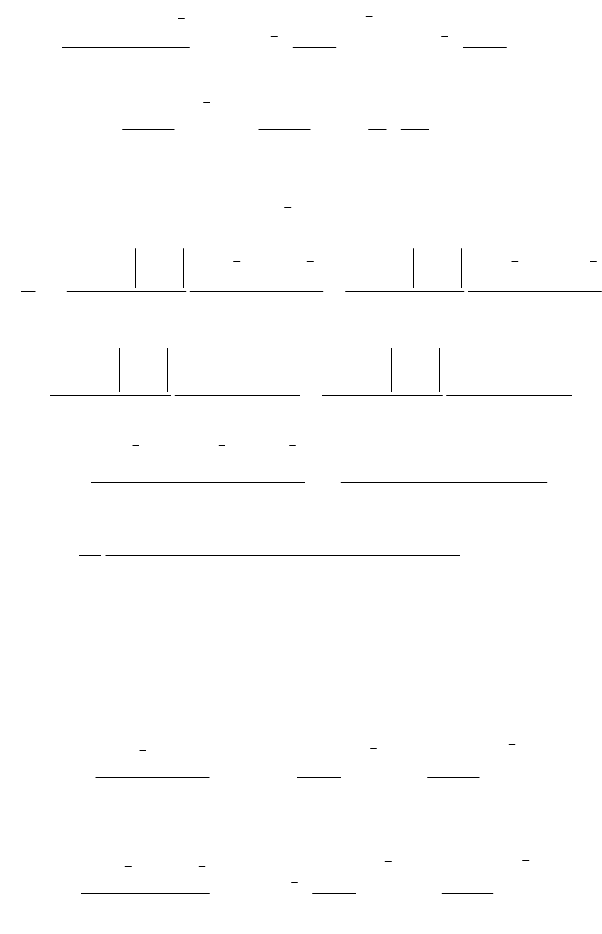
1

2

1

2

1

2

1

2

1

2/

k

x

k

y

k

x

k

x

k

x

k

x

y

U

x

U

UU



.

1

2

1























































k

x

k

x

k

x

F

x

P

y

U

x

U





(6.3)

Более подробно схема (6.2) выглядит следующим образом:

































h

UU

h

UU

h

UU

h

UU

k

ji

x

k

ji

x

k

ji

y

k

ji

y

k

ji

x

k

ji

x

k

ji

y

k

ji

y

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

,1,

,,

1,,

,,

,,1

,,

,1,

,,

22

222

2

1

2

1

2

1

2

1

2

1























2

1,,1,

2

,1,,1

22

2

1

2

1

2

1

h

UUU

h

UUU

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x



.

4

1

,

1

1,1

1

1,1

1

1,1

1

1,1





























k

ji

x

k

ji

k

ji

k

ji

k

ji

F

h

PPPP



(6.4)

В методе расщепления шаг по времени делится на 3 этапа

продолжительностью τ. На первом этапе расчет ведется лишь в

направлении Ox, на втором этапе – лишь в направлении Oy, на

третьем этапе учитываются неучтенные ранее слагаемые, не

содержащие U

x

. Для первого этапа имеем:

.

3

1

3

1

3

1

2





































k

x

k

x

k

x

k

x

k

x

U

x

U

UU





(6.5)

Для второго этапа:

.

3

2

3

2

3

1

3

1

3

2







































k

x

k

x

k

y

k

x

k

x

y

U

y

U

UU





(6.6)

Для третьего этапа:

16

.

1

3

2

























k

x

k

x

k

x

F

x

P

UU



(6.7)

Распишем схему для первого этапа:



















h

UU

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

3

1

3

1

3

1

,1,

,,

2



.

2

,1,,1,,1

,,

3

1

3

1

3

1

3

1

3

1

























h

UUU

h

UU

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x



(6.8)

Схема для второго этапа строится аналогично.

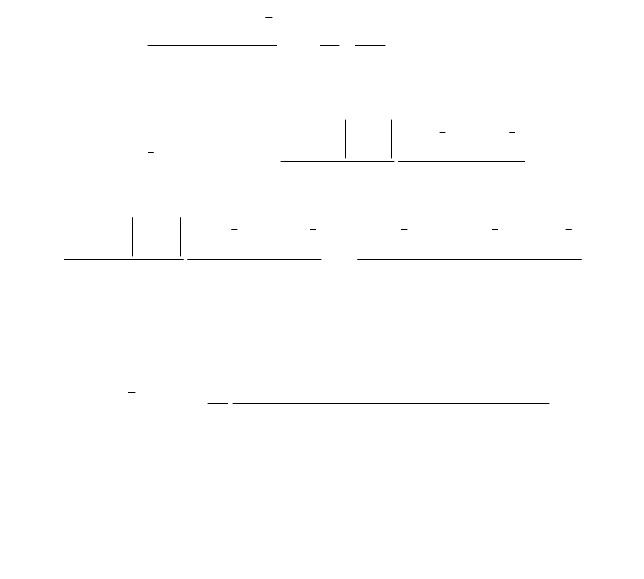
Схема для последнего этапа имеет вид:

.

4

1

,

1

1,1

1

1,1

1

1,1

1

1,1

,

1

,

3

2



































 k

ji

x

k

ji

k

ji

k

ji

k

ji

k

ji

x

k

ji

x

F

h

PPPP

UU





(6.9)

Как можно заметить, приведенные разностные схемы, как

в методе переменных направлений, так и в методе расщепления,

содержат по 3 неизвестных:











k

ji

x

k

ji

x

k

ji

x

UUU

,1,,1

,,

(для метода

переменных направлений κ=

1

/

2

, для метода расщепления κ=

1

/

3

) –

значения искомого поля скорости в новый момент времени. Как

же в таком случае можно решить эти разностные уравнения?

Перегруппировав слагаемые в уравнениях в обоих этапах метода

переменных направлений и в первых двух этапах метода

расщепления, уравнения можно привести к виду

.

,1,,1

i

k

ji

xi

k

ji

xi

k

ji

xi

fUcUbUa 









(6.10)

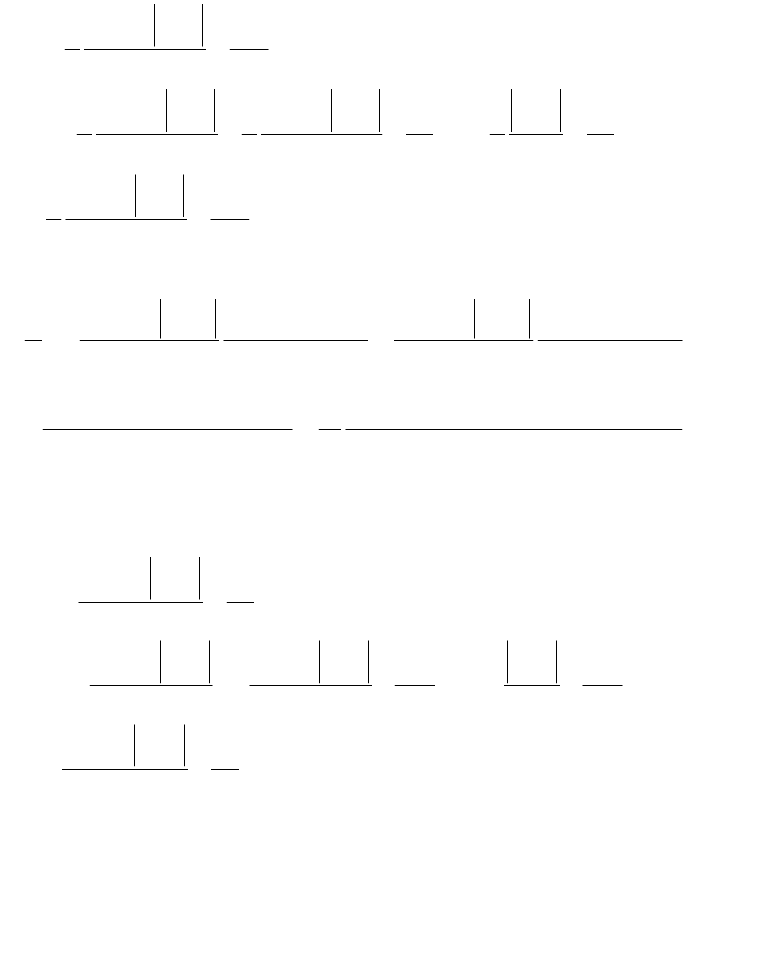
Так, например, в первом этапе метода переменных

направлений:

17

;

222

;

2

1

2222

1

;

222

2

,,

2

,

2

,,,,

2

,,

hh

UU

c

hh

U

hh

UU

h

UU

b

hh

UU

a

k

ji

x

k

ji

x

i

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

i

k

ji

x

k

ji

x

i

























.

4

1

2

222

1

,

1

1,1

1

1,1

1

1,1

1

1,1

2

1,,1,

,1,

,,

1,,

,,

,



















































k

ji

x

k

ji

k

ji

k

ji

k

ji

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

y

k

ji

y

k

ji

x

k

ji

x

k

ji

y

k

ji

y

k

ji

xi

F

h

PPPP

h

UUU

h

UU

h

UU

Uf







(6.11)

По методу расщепления схема получается проще. Для

первого этапа получаем такие коэффициенты:

;

2

,,

hh

UU

a

k

ji

x

k

ji

x

i











;

2

1

2

22

1

2

,

2

,,,,

hh

U

hh

UU

h

UU

b

k

ji

x

k

ji

x

k

ji

x

k

ji

x

k

ji

x

i

















;

2

,,

h

UU

c

k

ji

x

k

ji

x

i









.

,

k

ji

xi

Uf 

(6.12)

Для решения уравнения или, точнее, системы уравнений

(6.10) используется метод прогонки.

Представим







k

ji

x

U

,1

в виде

.

,,1

i

k

ji

xi

k

ji

x

MULU 







(6.13)

18

Аналогично можно записать:

.

1

,1

1

,





i

k

ji

xi

k

ji

x

MULU



(6.14)

Подставим (6.13) в (6.10):

.

,1,,

i

k

ji

xi

k

ji

xiii

k

ji

xii

fUcUbMaULa 







(6.15)

Перегруппировав, получим:

 

.

,1,

iii

k

ji

xi

k

ji

xiii

MafUcUbLa 





(6.16)

Принимая во внимание (6.14), находим рекуррентные

формулы для L

i

и M

i

:

.;

11

iii

i

iii

i

bLa

Maf

M

bLa

c

L













(6.17)

Таким образом, зная L

1

и M

1

, можно вычислить все L

i

и M

i

.

L

1

и M

1

можно найти из граничных условий (см. раздел 7). Если

дано граничное условие I рода, т.е. задано значение скорости на

границе:

,

,0

qU

j

x



где q – некоторая константа, то из равенства

(6.13) следует:

.

1

,1

1

MULq

k

j

x







(6.18)

Чтобы это равенство выполнялось для всех

,

,1



k

j

x

U

необходимо, чтобы:

.;0

11

qML 

(6.19)

Если дано граничное условие II рода, т.е. на границе

задана производная скорости по нормали к границе:

,

,0



















j

x

U

где λ – некоторая константа, то, раскрывая

производную











h

UU

k

j

x

k

j

x

,0,1

(6.20)

и принимая во внимание равенство (6.13), получим:

.;1

11

hML





(6.21)

19

Рис. 1

Итак, теперь все коэффициенты L

i

и M

i

найдены, и чтобы

найти все



k

ji

x

U

,

, остается лишь узнать





k

jN

x

U

,1

. Это значение

также находится из граничных условий. При граничном условии I

рода значение





k

jN

x

U

,1

известно. При граничном условии II рода



















 jN

x

U

,1

получаем:

.

,,1













h

UU

k

jN

x

k

jN

x

xx

(6.22)

Подставив вместо



k

jN

x

U

,

равенство (6.13) и сделав

соответствующие выкладки, получим

.

1

,1









x

N

k

jN

x

L

hM

U





(6.23)

Таким образом находятся все



k

ji

x

U

,

.

Итак, при использовании метода прогонки вначале

выполняется прогонка слева направо и находятся прогоночные

коэффициенты L

i

и M

i

, а затем – справа налево и находится поле

скоростей.

7. Граничные и начальные условия

Выбор граничных условий в значительной мере влияет на

получаемое решение. Поэтому выбору граничных условий

следует уделить должное внимание.

Здесь мы рассмотрим 3 вида границ – твердую стенку и

входную и выходную границы

(приточное и вытяжное отверстия).

На рис. 1 дано условие задачи о

20

Филатов Е.Ю., Ясинский Ф.Н. Математическое моделирование течений жидкостей и газов

Подождите немного. Документ загружается.