Федосеев В.В. и др. Экономико-математические методы и прикладные модели

Подождите немного. Документ загружается.

Оптимальные экономико-математические модели 111

задача в общем случае будет задачей невыпуклого програм-

мирования. Обычный подход заключается в стремлении

«свернуть» частные критерии в один обобщенный скаляр-

ный критерий, оптимизация которого приводит к оптималь-

ному решению задачи в целом. Формулировка подходящего

обобщенного критерия в зависимости от конкретных усло-

вий как раз и является основным вопросом, который изу-

чается в многокритериальной оптимизации.

В некоторых случаях вместо одного обобщенного критерия и

решения одной соответствующей задачи скалярной оптимиза-

ции предлагается рассматривать последовательность обобщен-

ных критериев и последовательность задач скалярной оптими-

зации. К сожалению, многие из описанных в литературе подоб-

ных процедур не всегда приводят к эффективным решениям.

Рассмотрим один из таких методов решения многокрите-

риальных задач: метод последовательных уступок.

Метод последовательных уступок решения задач много-

критериальной оптимизации применяется в случае, когда

частные критерии могут быть упорядочены в порядке убы-

вания их важности. Предположим, что все частные критерии

максимизируются и пронумерованы в порядке убывания их

•к

важности. Находим максимальное значение Zj первого по

важности критерия в области допустимых решений путем

решения однокритериальной задачи

Zi(X) -» max,

X eQ.

Затем, исходя из практических соображений и принятой

точности, назначается величина допустимого отклонения

5i > 0 (экономически оправданной уступки) критерия Z\ и

находится максимальное значение второго критерия Z

npn

условии, что значение первого критерия не должно откло-

няться от своего максимального значения более чем на ве-

личину допустимой уступки, т. е. решается задача:

{X) -> max,

X eQ.

112 Глава 3

Снова назначается величина уступки 82 > 0 по второму

критерию, которая вместе с первой уступкой используется для

нахождения условного максимума третьего частного критерия:

(X) -> max,

(X)

z\ - 6

(X) > Z

-5

X EQ.

Аналогичные процедуры повторяются до тех пор, пока не

будет выявлено максимальное значение последнего по важ-

ности критерия Z

при условии, что значение каждого из пер-

вых т - 1 частных критериев отличается от соответствующего

условного максимума не более чем на величину допустимой

уступки по данному критерию. Полученное на последнем

этапе решение считается оптимальным. Следует заметить,

что этот метод не всегда приводит к эффективному решению.

L. Пример 6. Решение задачи многокритериальной оптими-

зации методом последовательных уступок.

Пусть задача трехкритериальной оптимизации имеет вид:

Z\ = -*i + 2х

-> max (3.32)

= 2*i + х

-» max (3.33)

= хх - Зх

-> max (3.34)

1 < х

3 [. (3.35)

1 < х

< 4

Заметим, что так как коэффициенты при одних и тех же

переменных в данных частных критериях имеют разные

знаки, то в заданной области допустимых решений невоз-

можно одновременно улучшить все частные критерии, т. е.

в рассматриваемом случае область компромиссов (область

Парето) совпадает с областью допустимых решений (3.35).

Оптимальные экономико-Математические модели 113

Для определенности будем считать, что допустимые ус-

тупки по первым двум критериям заданы: 5i= 3; 62= 5/3.

Максимизируем функцию

Z\ в

области допустимых ре-

шений, т. е. решаем однокритериальную задачу (3.32), (3.35).

Это несложно сделать рассмотренным

гл.

графическим

методом решения задач линейного программирования

(см.

рис. 3.1).

4Н

77777

V///////////

Рис. 3.1

Максимум функции

при условиях (3.35) достигается

в точке

области Q с координатами (1;4), так что

данном

случае

д^

=1;

= 4; maxZ

Z^A)

= 7.

Переходим

максимизации функции

при условиях

(3.35)

дополнительном ограничении, позволяющем учесть,

что по критерию

нельзя уступать более чем на 6i. Так

как

нашем примере Z±

= 4, то дополнительное огра-

ничение будет иметь вид:

-Х

+ 2х

> 4.

(3.36)

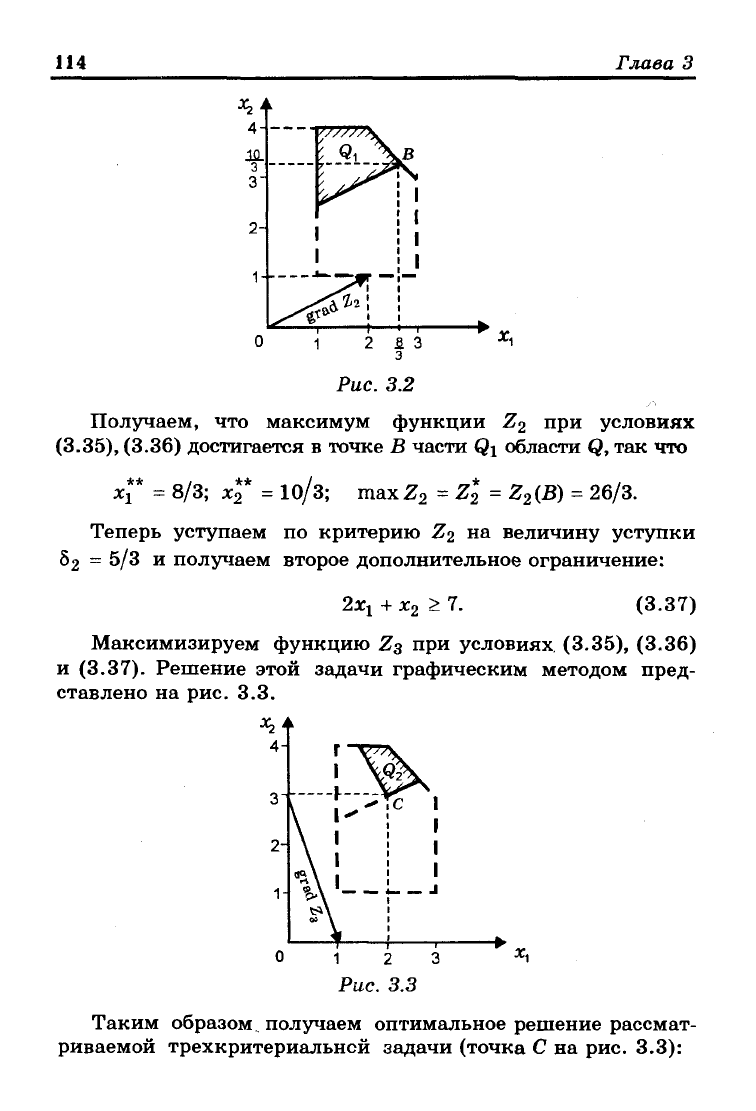
Задачу (3.33), (3.35), (3.36) также решаем графически

(рис.

3.2).

114

Глава 3

X, i

Ж.

•i

-7/ЛУХ

: Qi \

'S^\

—•

о 1 2 a. з *i

Puc.

3.2

Получаем, что максимум функции Z

при условиях

(3.35),

(3.36) достигается в точке В части Qi области Q, так что

х[* = 8/3;

х*

= ю/З; max Z

= z| = 2

(В) = 26/3.

Теперь уступаем по критерию Z

на величину уступки

= 5/3 и получаем второе дополнительное ограничение:

2х

+ х

> 7. (3.37)

Максимизируем функцию Z^ при условиях (3.35), (3.36)

и (3.37). Решение этой задачи графическим методом пред-

ставлено на рис. 3.3.

X,i

з-

«Л

ЪЛ

'^?bv

—•

0 12 3

Рис.

3.3

Таким образом получаем оптимальное решение рассмат-

риваемой трехкритериальнсй задачи (точка С на рис. 3.3):

Оптимальные экономико-математические модели 115

i - 2; х

Соответствующие значения частных критериев при этом

составляют:

= 4; Z

= 7; Z

= -7. J

3.5. Нелинейное и динамическое программирование;

понятие об имитационном моделировании

Задача нелинейного программирования формулируется

так же, как и общая задача оптимального программирова-

ния, т.е. в виде (3.38) — (3.40), со следующими требованиями

к целевой функции и допустимой области: целевая функ-

ция f(X) - f(x

,...,x

)unn (и) хотя бы одна из функций

(xi, х

,.. •, х

i = l,m являются нелинейными:

max(jam)f(x

,...,x

), (3.38)

(xi,x

,...,x

) {<,=,>}б

, i = l,m, (3.39)

Xj >0, j = l,n. (3.40)

Напомним, что для задач линейного программирования

характерно следующее:

• Множество допустимых решений выпукло. Это выпуклое

множество имеет конечное число вершин, называемых

обычно крайними (угловыми) точками.

• Множество всех точек Х1,...,зс

га-мерного пространства, в

которых целевая функция принимает заданное значение,

есть гиперплоскость (линия) уровня. Кроме того, гипер-

плоскости, соответствующие разным значениям целевой

функции, параллельны.

• Локальный max или min является также глобальным

max или min целевой функции на множестве допустимых

решений, т. е. не существует локального оптимума целевой

функции, отличного от глобального оптимума.

116 Глава 3

• Если оптимальное значение целевой функции ограничено,

то по крайней мере одна крайняя точка множества до-

пустимых решений является оптимальным решением.

Кроме того, начав с произвольной вершины множества

допустимых решений, можно достичь оптимума за конеч-

ное число шагов, причем на каждом шаге совершается пе-

реход только в соседнюю вершину. Окончательно данная

вершина является оптимальной тогда и только тогда, когда

значение целевой функции в ней по крайней мере не

меньше, чем значения целевой функции во всех примы-

кающих вершинах.

У произвольной задачи нелинейного программирования

некоторые или все приведенные выше свойства ЗЛП отсут-

ствуют. Вследствие этого задачи нелинейного программиро-

вания несравненно сложнее задач ЛП и для них не сущест-

вует общего универсального метода решения (аналогичного

симплексному методу).

Пример 7. Найти max и rain функции Z = f(x^, х

) = xf

при ограничениях

-х

<А

> 5

• х

О, х

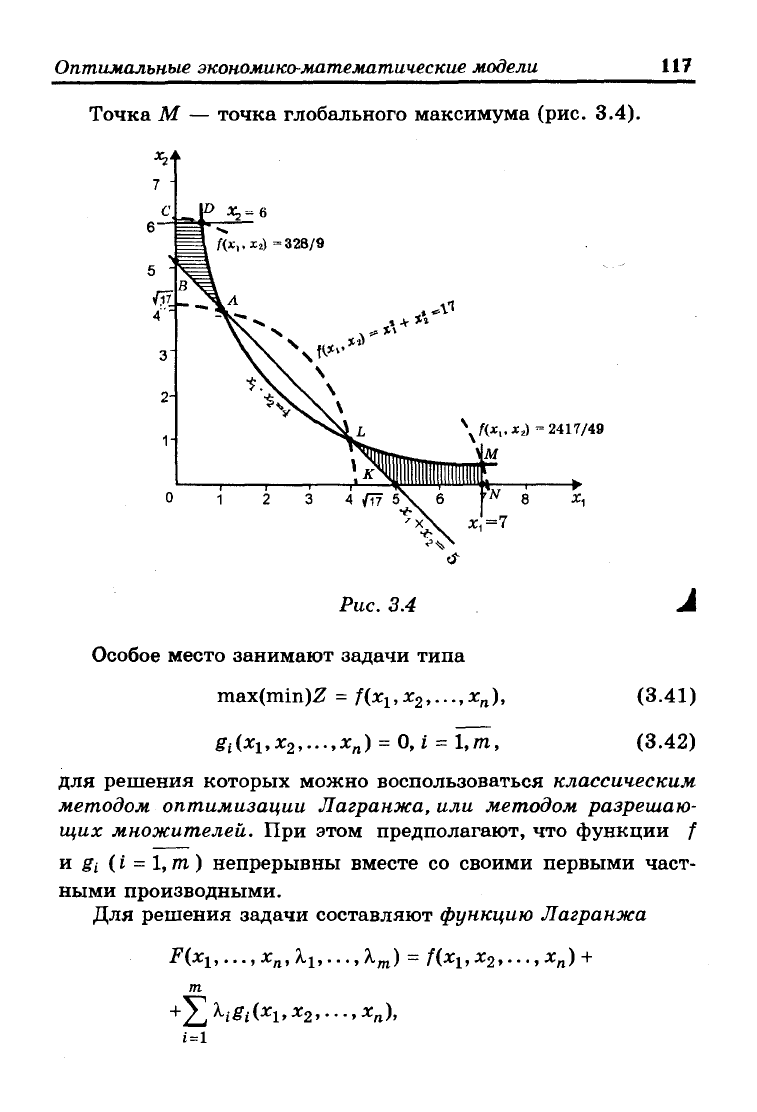
Линии уровня целевой функции {Z ~ const) представляют

собой окружности с центром в начале координат; область

допустимых решений не является выпуклой и состоит из

двух отдельных частей (на рис. 3.4 эти части заштрихова-

ны,

линии уровня показаны пунктиром). Минимальное зна-

чение функции Z = 17 достигается в точках А(1;4) и Д4;1).

Функция Z имеет два локальных максимума: в точке

328

D(2/3;6), где функция Z(D) = , и в точке М(7;4/7), в ко-

торой функция Z(M) = 2417/49.

Оптимальные экономико-математические модели

117

Точка М — точка глобального максимума (рис. 3.4).

4~*

\ «*,.**> "2417/49

Рис. 3.4

Особое место занимают задачи типа

max(min)Z = f(x

,...,x

,..-,x

) = 0, i = 1,т,

(3.41)

(3.42)

для решения которых можно воспользоваться классическим

методом оптимизации Лагранжа, или методом разрешаю-

щих множителей. При этом предполагают, что функции /

и g

(i = 1, т) непрерывны вместе со своими первыми част-

ными производными.

Для решения задачи составляют функцию Лагранжа

i>•••>х

,Х^,...,Х

) - f(xi,X2,-..,x

) +

+ / , ^i£j(-*l.*2> •••>

п)>

118

Глава 3

определяют частные производные этой функции по пере-

менным Xj (j = 1,п) и множителям Лагранжа A.j (i

1,т\

приравнивают их нулю и получают систему уравнений:

dF _ df

^, dg

дх

.Т.Ъ-£

°'!-

ox, ox, .

ox,

(34g)

, ч п -л

—- = g

,...,x

) = 0,1 = \,т.

В основе метода Лагранжа решения классической задачи

оптимизации (3.41), (3.42) лежит утверждение, что если

Z = f{*i,х

,...,х

) в точке X = (д^ ,х

,...,х

)имеет экс-

тремум, то существует такой вектор (A,j,

Х^,...

,Х

), что точ-

ка (x

,...,x

,Xi,X

,...,X

) является решением системы

(3.43).

Следовательно, решая систему (3.43), получаем мно-

жество стационарных точек, в которых функция Z может

иметь экстремальные значения. При этом, как правило, не-

известен способ определения точек глобального максимума

или минимума. Однако если решения системы найдены, то

для определения глобального максимума или минимума дос-

таточно найти значения функции в соответствующих точках

области определения.

Пример 8. Найти экстремум функции Z =

х-у

+ х

Л,

при ограничениях

= 2.

Решение. Составляем функцию Лагранжа

F(x^, х

, х

, Xi, Х

) = х^х

4-A,I(JCJ

+ х

2) +

(х

+ Хо

—

2),

дифференцируем ее по переменным

,х

,Х

и полу-

ченные выражения приравниваем нулю:

Оптимальные экономико-математические модели 119

Aj + х

^»

х^

+ Х± +

О»

• х

= О,

*2 -2 = О,

дг

+ *з ~ 2 = О.

Из первого и третьего уравнений следует, что Х

-х

поэтому

—

4Хо "Ь #3

^»

Хл 4- Хо — ^»

Хп ~Ь Хо = 4,

откуда х{* = х

= х

= 1 и Z = 2 . Поскольку, например,

точка (0;2;0) принадлежит допустимой области и в ней Z = О,

то делаем вывод, что точка (1;1;1) — точка глобального

максимума. Л

К классу задач нелинейного программирования, изучен-

ному наиболее основательно, относятся задачи с линейными

ограничениями и нелинейной целевой функцией. В общем

виде такая задача записывается следующим образом:

найти max(min)Z = f(x

,...,x

^ацХ] {<,=,>}b

,i = l,m;

Xj > О, j =

п.

Отметим, что даже для задач с линейными ограничения-

ми вычислительные методы разработаны лишь в тех случа-

ях, когда целевая функция имеет определенные свойства,

например, функция Z сепарабельная, т.е.

Z = f(x

,...,x

) = hiXi)

)+...+f

Чтобы гарантировать возможность отыскания оптимального

решения, на функции fAxA должны быть наложены доба-

120

Глава

вочные ограничения. Другим примером могут служить

за-

дачи,

которых целевая функция может быть записана как

сумма линейной

квадратичной форм, так что

п п

Z = f(x

,...,x

) =

Yu'Yj

j=i i=ij=i

= с

Х2+...+с

+...+d

xl.

Такие нелинейные задачи называются задачами квадра-

тичного программирования. Чтобы быть уверенным, что оп-

тимальное решение

и в

этом случае может быть найдено, на

величины dtj следует наложить некоторые ограничения.

Имеются достаточно эффективные методы решения задачи

выпуклого программирования, т.е. задачи минимизации

не-

линейной, но гладкой выпуклой функции при ограничениях,

заданных нелинейными неравенствами, определяющими вы-

пуклое множество переменных:

minf(x

,...,x

(3.44)

,...,х

) <b

l,m,

(3.45)

= Т~п. (3.46)

В случае максимизации

таких задачах целевая функ-

ция должна быть вогнутой. Симплексный алгоритм для ре-

шения общей задачи

ЛП

представляет собой итеративную

процедуру, с помощью которой точное оптимальное решение

может быть получено

за

конечное число шагов. Для задач

нелинейного программирования вычислительный метод, даю-

щий точное оптимальное решение

за

конечное число шагов,

удается построить

не

всегда. Здесь часто приходится согла-

шаться

на

использование методов, дающих только прибли-

женное решение или требующих для сходимости бесконечного

числа шагов.

Один

из

наиболее мощных методов решения задач нели-

нейного программирования состоит

преобразовании задачи

каким-либо образом

виду, допускающему применение сим-