Farin G. Curves and Surfaces for CAGD. A Practical Guide
Подождите немного. Документ загружается.


22 Chapter 2 Introductory Material
Qx o
o
Figure 2.5 Norm ellipses: a point set and an associated ellipse.
This method works even if the number of q/ does not equal that of the p/.
An obvious generalization v^orks in 3D. Applications are in image registration,
where two images (typically represented by point sets) have to be mapped to each
other.
2.4 Function Spaces
This section contains material that will later simplify our work by allowing very
concise notation. Although we shall try to develop our material with an emphasis
on geometric concepts, it will sometimes simplify our work considerably if we
can resort to some elementary topics from functional analysis. Good references
are the books by Davis [133] and de Boor
[138].
Let
C[a^
h\ be the set of all real-valued continuous functions defined over the
interval
\a^
h\ of the real axis. We can define addition and multiplication by a
constant for elements /^,g € C[a, h\ by setting (af + Pg)(t) = af(t) + Pg(t) for all
t 6
[a,
b].
With these definitions, we can easily show that
C[a^
b] forms a linear
space over the reals. The same is true for the sets C^[^,
fe],
the sets of all real-
valued functions defined over
[a,
b]
that are fe-times continuously differentiable.
Furthermore, for every k, C^^^ is a subspace of C^.
We say that n functions
/^i,...,
/^
G
C[a^
b]
are linearly independent if ^
Cifi
=
0 for all t e
[a^
b]
implies ci = .. . = c^ = 0.
We mention some subspaces of C[a,
b]
that will be of interest later. The spaces
V^ of all polynomials of degree n are
p'^it)
= ao-\- ait + ait^ +
• • •
+
aj""-,
t e
[a,
b].
2.4 Function Spaces 23
For fixed
n^
the dimension of V^\sn-\-1: each p^ e V^ is determined uniquely by
the
w
+ 1 coefficients
UQ^,
..., a^. These can be interpreted as a vector in {n + 1)-
dimensional finear space R"+\ which has dimension
w
+ 1. We can also name
a basis for V^: the monomials
\,t,t^^.
.. ,t^ are
w
+ 1 finearly independent
functions and thus form a basis.
Another interesting class of subspaces of C[^,
b]
is given by piecewise linear
functions: let ^ =
^Q
< ^l < '
* *
<
^w
= ^ be a partition of the interval
[a,
b\ A
continuous function that is linear on each subinterval [^/, tij^^ is called a piecewise
linear function. Over a fixed partition of
[a.,
b\ the piecev^ise linear functions form
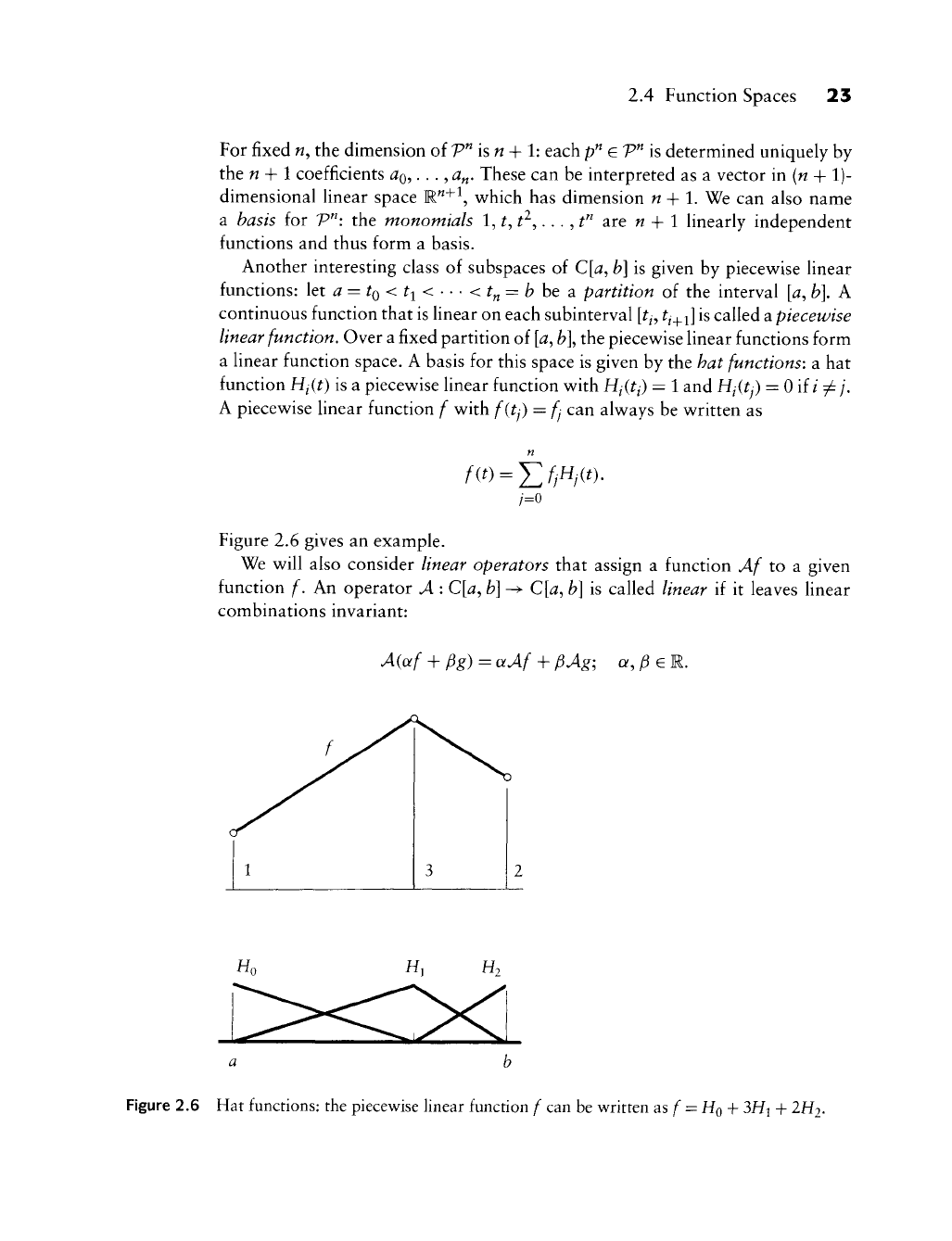
a linear function space. A basis for this space is given by the hat functions: a hat
function Hi{t) is a piecev^ise linear function v^ith H^(^^) =
1
and H^(^y) = 0 if
/ /=
/•
A piecew^ise linear function f v^ith f{tj) = ^ can alw^ays be v^ritten as
n
f{t) =
Y.fi^i^^)'
Figure 2.6 gives an example.
We v^ill also consider linear operators that assign a function Af to a given
function f. An operator ^ : C[a,
b]
-^ C[a,
b]
is called linear if it leaves linear
combinations invariant:
A(af + Pg) = aAf + pAg; a, ^
G
R.
Figure 2.6 Hat functions: the piecewise linear function f can be written as
/"
=
HQ
+ 3Hi + 2H2

24 Chapter 2 Introductory Material
An example is given by the derivative operator that assigns the derivative f^ to a
given function f: Af = f.
2.5 Problems
1 Of all affine maps, shears seem to be the least familiar to most people.^
Construct a matrix that maps the unit square with points (0,0), (1,0), (1,1),
(0,1) to the parallelogram v^ith image points (0,0), (1,0), (2,1), (1,1).
* 2 We have seen that affine maps leave the ratio of three collinear points
constant (i.e., they are ratio preserving). Show that the converse is also
true:
every ratio-preserving map is affine.
* 3 Show that the n-\-l functions fi(t) = f; / =
0,...,«
are linearly indepen-
dent.
P1 Fix two distinct points a, b on the x-axis. Let a third point x trace out all the
X-axis. For each location of x, plot the value of the function ratio(a, x, b),
thus obtaining a graph of the ratio function.
4 Recall that Figure 2.4 illustrates a shear.

Linear Interpolation
M
ost of the computations that we use in CAGD may be broken down into
seemingly trivial steps—sequences of linear interpolations. It is therefore impor-
tant to understand the properties
of
these basic building blocks. This chapter
explores those properties and introduces
a
related concept, called blossoms.
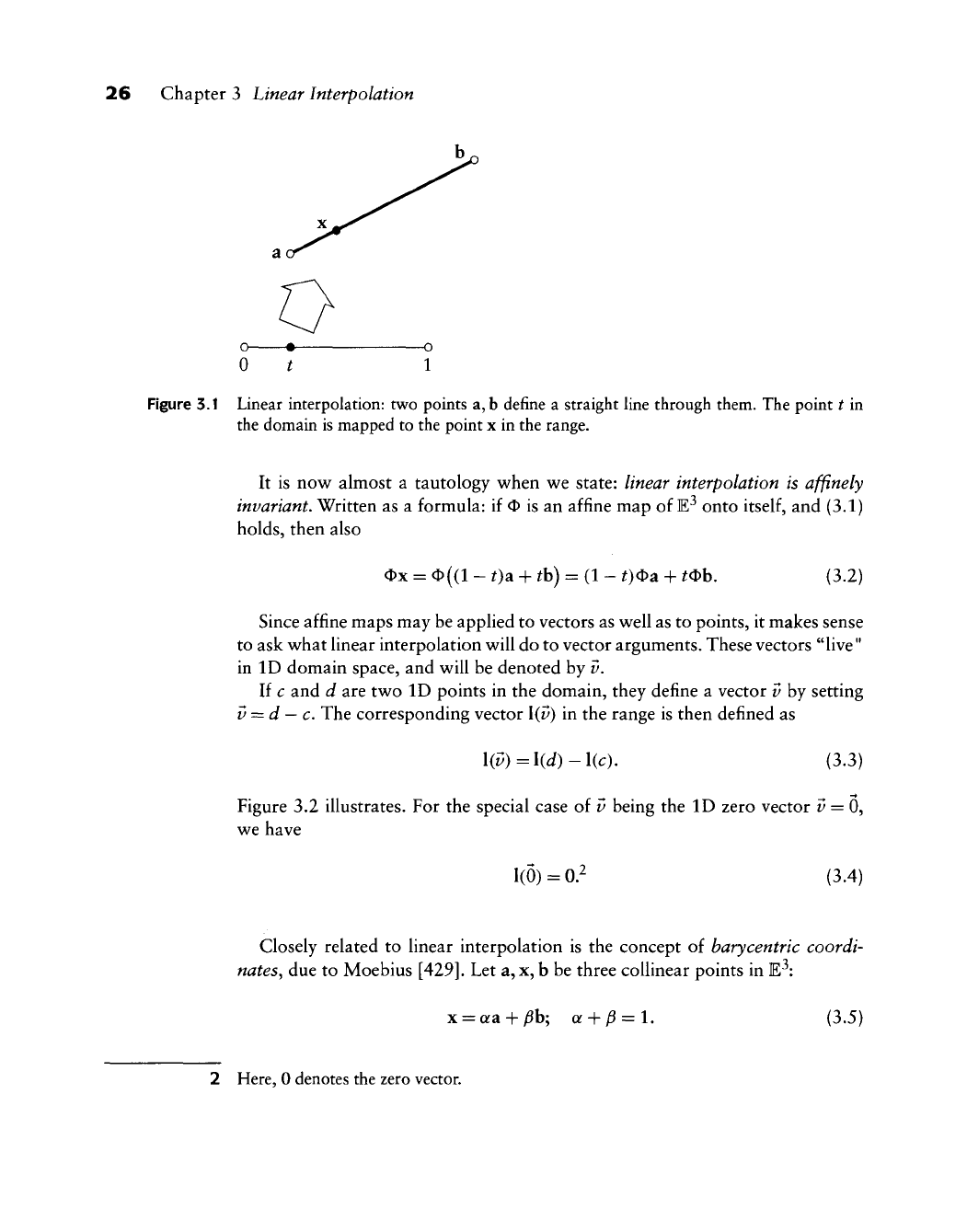
5.1 Linear Interpolation
Let a, b be two distinct points in E^. The set of all points
x e
E^ of the form
x
= x(t) =
(l-t)ei-^th; t eR (3.1)
is called the straight line through a and
b.
Any three (or more) points on a straight
line are said to be collinear.
For
^
=
0, the straight line passes through a and for
^
=
1, it passes through b.
For 0 < ^
<
1, the point x is between
a
and b, whereas for all other values of
t
it
is outside; see Figure 3.1.
Equation (3.1) represents
x
as
a
barycentric combination
of
two points
in
E-^. The same barycentric combination holds for the three points 0, t, 1 in E^:
t =
(l
—
t)-0-\-t'l.Sotis related to 0 and
1
by the same barycentric combination
that relates x to a and b. Hence, by the definition of affine maps, the three points
a,
X,
b are an affine map of the three ID points 0, ^, 1! Thus linear interpolation
is an affine map of the real line onto a straight line in E^.^
1 Strictly speaking, we should therefore use the term affine interpolation instead of
linear
interpolation.
We use linear interpolation because its use is so widespread.
25
26 Chapter 3 Linear Interpolation
0
t 1
Figure 3.1 Linear interpolation: two points a,b define a straight hne through them. The point
t
in
the domain is mapped to the point x in the range.
It
is
now almost
a
tautology when we state: linear interpolation is affinely
invariant. Written as
a
formula:
if 0
is an affine map onto
itself,
and (3.1)
holds,
then also
<Dx
=
^{(1
-
t)a
+
^b)
=
(1
-
t)<t>2i
+ t^h. (3.2)
Since affine maps may be applied to vectors as well as to points, it makes sense
to ask what linear interpolation will do to vector arguments. These vectors "live"
in ID domain space, and will be denoted by
v.
If c and
d
are two ID points in the domain, they define
a
vector
v
by setting
y
—
d
—
c. The corresponding vector \(v) in the range is then defined as
\{v)=\{d)-\{c),
(3.3)
Figure 3.2 illustrates. For the special case
of v
being the ID zero vector
? =
0,
we have
1(0)
=
0.^
(3.4)
Closely related
to
linear interpolation
is
the concept
of
barycentric coordi-
nates^ due to Moebius
[429].
Let a, x, b be three coUinear points in E^:
x
=
aa
+
)Sb;
a +
jS
= l. (3.5)
2 Here, 0 denotes the zero vector.

3.1 Linear Interpolation 27
-o«-
0 1 1
Figure 3.2 Linear interpolation: the vector
1
in the domain is mapped to the vector
1(1)
in the range.
Then a and ^ are called harycentric coordinates of x with respect to a and b.
Note that by our previous definitions, x is a barycentric combination of a and b.
The connection between barycentric coordinates and linear interpolation is
obvious: we have a = \
—
t and ^
—
t. This shows, by the way, that barycentric
coordinates do not always have to be positive: for t ^
[0,1],
either a or ^ is
negative. For any three collinear points a, b, c, the barycentric coordinates of b
with respect to a and c are given by
voli(b,c)
a = —-^ ,
voli(a,c)
voli(a,b)
voli(a, c)'
where vol^ denotes the one-dimensional volume, which is the signed distance
between two points. Barycentric coordinates are not only defined on a straight
line,
but also on a plane. Section 3.5 has more details.
Another important concept in this context is that of ratios. The ratio of three
collinear points a, b, c is defined by
ratio(a, b, c) =
voli(a,b)
(3.6)
voli(b,c)
If a and ^ are barycentric coordinates of b with respect to a and c, it follows that
ratio(a, b, c) =
(3.7)

28 Chapter 3 Linear Interpolation
The barycentric coordinates of a point do not change under affine maps, and
neither does their quotient. Thus the ratio of three cohinear points is not affected
by affine transformations. So if (3.7) holds, then also
ratio(4)a, Ob, Oc) = -, (3.8)
a
where O is an affine map. This property may be used to compute ratios efficiently.
Instead of using square roots to compute the distances between points a, x,
and b, we would project them onto one of the coordinate axes and then use
simple differences of their x- or ^-coordinates.^ This shortcut works since parallel
projection is an affine map!
Equation (3.8) states that affine maps are ratio preserving. This property may
be used to define affine maps. Every map that takes straight lines to straight lines
and is ratio preserving is an affine map.
The concept of ratio preservation may be used to derive another useful prop-
erty of linear interpolation. We have defined the straight line segment [a, b] to be
the affine image of the unit interval
[0,1],
but we can also view that straight line
segment as the affine image of any interval
[a,,
b].
The interval [^,
b]
may itself be
obtained by an affine map from the interval [0,1] or vice versa. With t € [0,1]
and u
G
[a,
b\ that map is given by t = (u
—
a)/(b
—
a). The interpolated point
on the straight line is now given by both
x(t) = (1 - t)a + ^b
and
x(u) = a + b. (3.9)
b
—
a b
—
a
Since
a^
w,
b and 0, ^, 1 are in the same ratio as the triple a, x, b, we have shown
that linear interpolation is invariant under affine domain transformations. By
affine domain transformation, we simply mean an affine map of the real fine
onto
itself.
The parameter t is sometimes called a local parameter of the interval
A more general way to express this is by saying that any barycentric com-
bination of three domain points r, s, t (not necessarily involving any interval
endpoints) carries over to the corresponding range points:
s = {l-ot)r + at=^ x(s) = (1 - Qf)x(r) + ax(0. (3.10)
3 But be sure to avoid projection onto the x-axis if
the
three points are parallel to the y-axis!

3.2 Piecewise Linear Interpolation 29
A concluding remark: we have demonstrated the interplay between the two
concepts of linear interpolation and ratios. In this book, we will often describe
methods by saying that points have to be collinear and must be in a given
ratio.
This is the geometric (descriptive) equivalent of the algebraic (algorithmic)
statement that one of the three points may be obtained by linear interpolation
from the other two.
5.2 Piecewise Linear Interpolation
Let bo,... ,b„
G
E^ form a polygon B. This polygon consists of a sequence of
straight line segments, each interpolating to a pair of points
b^,
b^_^i.
It is therefore
also called the piecewise linear interpolant VC to the points b^. If the points b^
lie on a curve c, then B is said to be a piecewise linear interpolant to c, and we
write
B
=
H:C.
(3.11)
One of the important properties of piecewise linear interpolation is affine
invariance. If the curve c is mapped onto a curve Oc by an affine map O, then
the piecewise linear interpolant to Oc is the affine map of the original piecewise
linear interpolant:
P£Oc = ^ VLz, (3.12)
Another property is the variation diminishing property. Consider a continuous
curve c, a piecewise linear interpolant VC c, and an arbitrary plane. Let cross c be
the number of crossings that the curve c has with this plane, and let cross(7X c)
be the number of crossings that the piecewise linear interpolant has with this
plane. (Special cases may arise; see Section 3.8.) Then we always have
cross(P£ c) < cross c. (3.13)
This property follows from a simple observation: consider two points b/, hj^i.
The straight line segment through them can cross a given plane at one point at
most, whereas the curve segment from c that connects them may cross the same
plane in many arbitrary points. The variation diminishing property is illustrated
in Figure 3.3.

30 Chapter
3
Linear Interpolation
Figure
3.3
The variation diminishing property:
a
piecewise hnear interpolant
to a
curve has
no
more
intersections with
any
plane than
the
curve
itself.
5.5
Menelaos' Theorem
We
use the
concept
of
piecewise linear interpolation
to
prove
one of the
most
important geometric theorems
for the
theory
of
CAGD: Menelaos' theorem.
This theorem
can be
used
for the
proof
of
many constructive algorithms,
and
its importance
v^as
already realized
by de
Casteljau
[146] and
W. Boehm
[67].
Referring
to
Figure
3.4,
w^e define
b[0,
^]
=
(1
-
^)bo
+ thi,
b[s,
0]
=
(1
- s)bo + sbi,
b[l,^]=(l-^)bi
+ fb2,
b[s,l]
=
(l-s)bi
+ sb2.
Let
us
further define
tv^o
points
b[s,
^]
=
(1
-
Ob[s, 0]
+ th[s,
1]
and
b[^
s]
= (1 -
s)b[0, t]
+ sh[t,
1]. (3.14)
Menelaos' theorem
now
states that these points
are
identical:
b[5,^]
= b[^4
(3.15)
For
a proof, we
simply verify that
b[s,
t]
= h[t, s\ = {l- t){l - s)bo + [(1 - t)s + t{l - s)]bi +
sth2. (3.16)
Some interesting special cases
are
given
by b[0, 0] = bo or by
b[0,1]
= b^.
Equation (3.15)
is a
"CAGD version"
of the
original Menelaos' theorem,
which
may be
stated
as (see
Coxeter [130]):

3.4 Blossoms 31
Figure 3.4 Menelaos' theorem: the point b[s,
t]
may be obtained from Hnear interpolation at t or
at s.
ratio(b[s, l],b[l,4bi)
•
ratio(bi,b[0,4b[s, 0])-
ratio(b[s, 0],b[s, 4b[s, 1]) =
-1.
(3.17)
The proof of (3.17) is a direct consequence of (3.15). Note the ordering of points
in the second ratio! Menelaos' theorem is closely related to Ceva's, which is given
in Section 3.5.
5.4 Blossoms
The bivariate function b[^i, ti] from (3.16) will be very important for the remain-
der of this book. Functions of that type are called blossoms. Before we introduce
the general concept, we will further explore properties of (3.16).
The first property is called symmetry. It states that the order of the blossom
arguments does not matter—which is exactly Menelaos' theorem.
In Section 3.1, we saw that linear interpolation carries domain relationships
over to corresponding range relationships; see (3.10). Since blossoms are evalu-
ated using linear interpolations, we now have: if the first argument ti of a blossom
is a barycentric combination of two (or more) ID points r and s, we may compute
the blossom values for each argument and then form their barycentric combina-
tion:
h[ar + ^s,
t2]
= ah[r, ti] + ^h{s, til a +
^6
= 1. (3.18)
Equation (3.18) states that the blossom b is affine with respect to its first argu-
ment, but it is affine for the second one as well because of the symmetry property.
This is the reason the blossom is called multiaffine—the second of its main prop-
erties.
For a third property, we study what happens if both blossom arguments are
equal: ti = t2 = t. Then the expression b[^, t\ denotes a point that depends on
