Everitt B.S. The Cambridge Dictionary of Statistics

Подождите немного. Документ загружается.

Galton^Watson process: A commonly used name for what is more properly called the

Bienaymé–Galton–Watson process.

GAM: Abbreviation for geographical analysis machine and generalized additive models.

Gambler’sfallacy: The belief that if an event has not happened for a long time it is bound to occur

soon. [Chance Rules , 2nd edition, 2008, B. S. Everitt, Springer, New York.]

Gambler’sruinproblem: A term applied to a game in which a player wins or loses a ﬁxed amount

with probabilities p and q (p 6¼ q). The player’s initial capital is z and he plays an adversary

with capital a z. The game continues until the player’s capital is reduced to zero or

increased to a, i.e. until one of the two players is ruined. The probability of ruin for the player

starting with capital z is q

given by

ðq=pÞ

ðq=pÞ

ðq=pÞ

 1

[KA2 Chapter 24.]

Gambling: The art of attempting to exchange something small and certain, for something large and

uncertain. Gambling is big business; in the US, for example, it is at least a $40-billion-a-year

industry. Popular forms of gambling are

national lotteries

, roulette and horse racing. For

these (and other types of gambling) it is relatively easy to apply statistical methods to

discover the chances of winning, but in no form of gambling does a statistical analysis

increase your chance of winning. [Chance Rules, 2nd edn, 2008, B. S. Everitt, Springer,

New York.]

Gametheory: The branch of mathematics that deals with the theory of contests between two or more

players under speciﬁed sets of rules. The subject assumes a statistical aspect when part of the

game proceeds under a chance scheme. Game theory has a long history of being applied to

security, beginning with military applications, and has also been used in the context of arms

control. [Simulation and Gaming, 2003, 34, 319–337.]

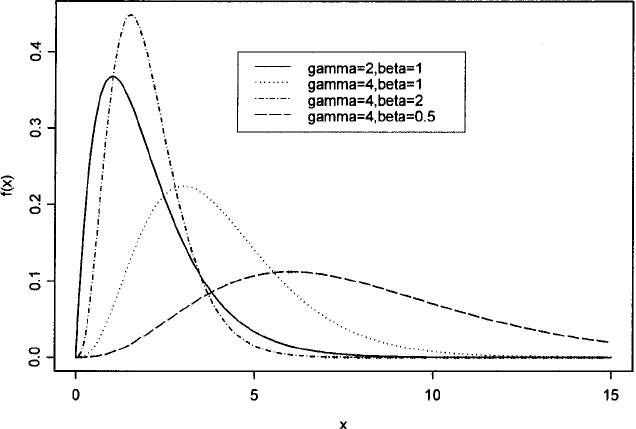
Ga mma d ist ri but i on: The probability distribution, f(x), given by

f ðxÞ¼



γ1

expðx=βÞ

βGðγÞ

; 0  x

1; β

0; γ

β is a

scale parameter

and γ a

shape parameter

. Examples of the distribution are shown in

Fig. 67. The mean, variance,

skewness

and

kurtosis

of the distribution are as follows

mean ¼ βγ

variance ¼ β

skewness ¼ 2γ



kurtosis ¼ 3 þ

The distribution of u ¼ x=β is the standard gamma distribution with corresponding density

function given by

f ðuÞ¼

γ1

x

GðγÞ

[STD Chapter 18.]

Ga mma functi o n: The function Γ deﬁned by

179

GðrÞ¼

r1

t

where r

0(r need not be an integer). The function is recursive satisfying the relationship

Gðr þ 1Þ¼rGðrÞ

The integral

r1

t

is known as the incomplete gamma function.

Gap statistic: A statistic for estimating the number of clusters in applications of

cluster analysis

Applicable to virtually any clustering method, but in terms of

K-means cluster analysis

, the

statistic is deﬁned speciﬁcally as

Gap

ðkÞ¼E



½logðW

Þ logðW

where W

is the pooled within-cluster sum of squares around the cluster means and E



denotes expectation under a sample of size n from the reference distribution. The estimate of

the number of clusters,

k, is the value of k maximizing Gap

(k) after the sampling distribution

has been accounted for. [Journal of the Royal Statistical Society, Series B, 2001, 63,411–23.]

Gap-straggler method: A procedure for partitioning of treatment means in a

one-way design

under the usual normal theory assumptions. [Biometrics , 1949, 5,99–114.]

Gap time: The time between two successive events in survival data in which each individual subject

can potentially experience a series of events. An example is the time from the development

of AIDS to death. [Biometrika , 1999, 86,59–70.]

Garbage i n garbage out: A term that draws attention to the fact that sensible output only follows

from sensible input. Speciﬁcally if the data is originally of dubious quality then so also will

be the results.

Fig. 67 Gamma distributions for a number of parameter values.

180

Gardner, Martin (1940^1993): Gardner read mathematics at Durham University followed by a

diploma in statistics at Cambridge. In 1971 he became Senior Lecturer in Medical Statistics

in the Medical School of Southampton University. Gardner was one of the founders of the

Medical Research Council’s Environmental Epidemiology Unit. Worked on the geograph-

ical distribution of disease, and, in particular, on investigating possible links between

radiation and the risk of childhood leukaemia. Gardner died on 22 January 1993 in

Southampton.

GA USS: A high level programming language with extensive facilities for the manipulation of matrices.

[Aptech Systems, P.O. Box 250, Black Diamond, WA 98010, USA. Timberlake Consulting,

Unit B3, Broomsley Business Park, Worsley Bridge Road, London SE26 5BN, UK.]

Gauss, Karl Friedrich (1777^1855): Born in Brunswick, Germany, Gauss was educated at the

Universities of Göttingen and Helmstedt where he received a doctorate in 1799. He was a

prodigy in mental calculation who made numerous contributions in mathematics and statistics.

He wrote the ﬁrst modern book on number theory and pioneered the application of mathematics

to such areas as gravitation, magnetism and electricity–the unit of magnetic induction was

named after him. In statistics Gauss’ greatest contribution was the development of

least squares

estimation

under the label ‘the combination of observations’. He also applied the technique to

the analysis of observational data, much of which he himself collected. The normal curve is also

often attributed to Gauss and sometimes referred to as the Gaussian curve, but there is some

doubt as to whether this is appropriate since there is considerable evidence that it is more

properly due to

de Moivre

. Gauss died on 23 February 1855 in Göttingen, Germany.

Gaussian distribution: Synonym for normal distribution.

Ga ussian M a rk ov rando m fi eld: A multivariate normal random vector that satisﬁes certain

conditional independence

assumptions. Can be viewed as a model framework that contains

a wide range of statistical models, including models for images,

time-series, longitudinal

data

, spatio-temporal processes, and graphical models. [Gaussian Markov Random Fields:

Theory and Applications, 2005, H. Rue and L. Held, Chapman and Hall/CRC, Boca Raton.]

Gaussian process: A generalization of the normal distribution used to characterize functions. It is

called a Gaussian process because it has Gaussian distributed ﬁnite dimensional marginal

distributions. A main attraction of Gaussian processes is computational tractability. They are

sometimes called Gaussian random ﬁelds and are popular in the application of

nonpara-

metric Bayesian models

.[Gaussian Processes for Machine Learning, 2006, C. E.

Rasmussen and C. K. I. Williams, MIT Press, Boston.]

G aussia n quad ra ture: An approach to approximating the integral of a function using a weighted

sum of function values at speciﬁed points within the domain of integration. n-point Gaussian

quadrature involves an optimal choice of quadrature points x

and quadrature weights w

for

i =1,...,n that yields exact results for polynomials of degree 2n–1 or less. For instance, the

Gaussian quadrature approximation of the integral [−∞, ∞] for a function f(x) becomes

1

f ðxÞdx 

i¼1

f ðx

Þ:

[Generalized Latent Variable Modeling: Multievel, Longitudinal and Structural Equation

Models, 2004, A. Skrondal and S. Rabe-Hesketh, Chapman and Hall/CRC, Boca Raton.]

Gaussian random field: Synonymous with Gaussian process.

181

Gauss^Markov theorem: A theorem that states that if the error terms in a

multiple regression

have the same variance and are uncorrelated, then the estimators of the parameters in the

model produced by

least squares estimation

are better (in the sense of having lower

dispersion about the mean) than any other unbiased linear estimator. See also best linear

unbiased estimator. [MV1 Chapter 7.]

G a uss- Newto n meth od: A procedure for minimizing an objective function that is a sum of

squares. The method is similar to the

Newton-Raphson method

but with the advantage of

not requiring second derivatives of the function.

Geary’sratio: A test of normality, in which the test statistic is the ratio of the

mean deviation

of a

sample of observations to the standard deviation of the sample. In samples from a normal

distribution, G tends to

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð2=pÞ

as n tends to inﬁnity. Aims to detect departures from a

mesokurtic curve

in the parent population. [Biometrika, 1947, 34, 209–42.]

GEE : Abbreviation for generalized estimating equations.

Gehan’s generalized Wilcoxon test: A

distribution free method

for comparing the survival

times of two groups of individuals. See also Cox–Mantel test and log-rank test.[Statistics

in Medicine, 1989, 8, 937–46.]

Geisser, Seymour (1929^2004): Born in New York City, Geisser graduated from the City College

of New York in 1950. From New York he moved to the University of North Carolina to

undertake his doctoral studies under the direction of

Harold Hotelling

. From 1955 to 1965

Geisser worked at the US National Institutes of Health as a statistician, and from 1960 to 1965

was also a Professorial Lecturer at George Washington University. He made important

contributions to

multivariate analysis

and prediction. Geisser died on 11 March 2004.

Gene: A DNA sequence that performs a deﬁned function, usually by coding for an amino acid sequence

that forms a protein molecule. [Statistics in Human Genetics, 1998, P. Sham, Arnold,

London.]

Gene ^ environment interaction: The interplay of genes and environment on, for example, the

risk of disease. The term represents a step away from the argument as to whether nature or

nurture is the predominant determinant of human traits, to developing a fuller understanding

of how genetic makeup and history of environmental exposures work together to inﬂuence

an individual’s traits. [The Lancet, 2001, 358, 1356–1360.]

Gene frequencyesti mation: The estimation of the frequency of an

allele

in a population from the

genotypes

of a sample of individuals. [Statistics in Human Genetics, 1998, P. Sham, Arnold,

London.]

Gene mappi ng: The placing of

genes

onto their positions on chromosomes. It includes both the

construction of marker maps and the localization of genes that confer susceptibility to

disease. [Statistics in Human Genetics, 1998, P. Sham, Arnold, London.]

General Household Survey: A survey carried out in Great Britain on a continuous basis since

1971. Approximately 100 000 households are included in the sample each year. The main

aim of the survey is to collect data on a range of topics including household and family

information, vehicle ownership, employment and education. The information is used by

government departments and other organizations for planning, policy and monitoring

purposes.

Generallocation model: A model for data containing both continuous and categorical variables.

The categorical data are summarized by a

contingency table

and their

marginal distribution

182

by a

multinomial distribution

. The continuous variables are assumed to have a

multivariate

normal distribution

in which the means of the variables are allowed to vary from cell to cell

of the contingency table, but with the

variance-covariance matrix

of the variables being

common to all cells. When there is a single categorical variable with two categories the

model becomes that assumed by

Fisher’s linear discriminant analysis

.[Annals of Statistics,

1961, 32, 448–65.]

Generalizability theory : A theory of measurement that recognizes that in any measurement

situation there are multiple (in fact inﬁnite) sources of variation (called facets in the theory),

and that an important goal of measurement is to attempt to identify and measure

variance

components

which are contributing error to an estimate. Strategies can then be implemented

to reduce the inﬂuence of these sources on the measurement. [Statistical Evaluation of

Measurement Errors, 2004, G. Dunn, Arnold, London.]

Generalized additive mixed models (GA M M ): A class of models that uses additive non-

parametric functions, for example,

splines

, to model covariate effects while accounting for

overdispersion

and correlation by adding

random effects

to the additive predictor. [Journal

of the Royal Statistical Society, Series B, 1999, 61, 381–400.]

Generalized additive models: Models which use smoothing techniques such as

locally weighted

regression

to identify and represent possible non-linear relationships between the explan-

atory and response variables as an alternative to considering polynomial terms or searching

for the appropriate transformations of both response and explanatory variables. With these

models, the

link function

of the expected value of the response variable is modelled as the

sum of a number of smooth functions of the explanatory variables rather than in terms of the

explanatory variables themselves. See also generalized linear models and smoothing.

[Generalized Additive Models, 1990, T. Hastie and R. Tibshirani, Chapman and Hall/CRC

Press, London.]

Generalized distance: See Mahalanobis D

Generalized estimating equations (GEE): Technically the multivariate analogue of

quasi-likelihood

with the same feature that it leads to consistent inferences about mean

responses without requiring speciﬁc assumptions to be made about second and higher order

moments

. Most often used for likelihood-based inference on

longitudinal data

where the

response variable cannot be assumed to be normally distributed. Simple models are used for

within-subject correlation and a working correlation matrix is introduced into the model

speciﬁcation to accommodate these correlations. The procedure provides consistent

estimates for the mean parameters even if the covariance structure is incorrectly speciﬁed.

The method assumes that missing data are

missing completely at random

, otherwise the

resulting parameter estimates are biased. An amended approach, weighted generalized

estimating equations, is available which produces unbiased parameter estimates under the

less stringent assumption that missing data are

missing at random

. See also sandwich

estimator.[Analysis of Longitudinal Data, 2nd edition, 2002, P. J. Diggle, P. J. Heagerty,

K.-Y. Liang and S. Zeger, Oxford Science Publications, Oxford.]

Ge nera lized ga mma di st ributi o n: Synonym for Creedy and Martin generalized gamma

distribution.

Generalized least squares (GLS): An estimator for the regression parameter vector β in the

multivariate linear regression model

y ¼ Xβ þ

’

183

where y is the vector of all n responses, X is a covariate matrix where the n covariate

vectors are stacked, and

’

a residual error vector. For the general case where

’

has a

variance-covariance matrix

Σ, the generalized least squares estimator of β is

GLS

¼ðX

1

XÞ

1

In practice Σ is unknown and estimated by the sample covariance matrix,

S yielding the

feasible generalized least squares (FGLS) estimator

FGLS

¼ðX

1

XÞ

1

In the special case where S ¼ 

I,the

ordinary least squares (OLS)

estimator is obtained.

[Multivariate Analysis, 1979, K. V. Mardia, J. T. Kent and J. M. Bibby, Academic, New York.]

Generalized linear mixed models (GLMM):

Generalized linear models

extended to include

random effects

in the linear predictor. See multilevel models and mixed-effects logistic

regression.

Generalized linear models: A class of models that arise from a natural generalization of ordinary

linear models. Here some function (the link function) of the expected value of the response

variable is modelled as a linear combination of the explanatory variables, x

; x

; ...; x

, i.e.

f ðEðyÞÞ ¼ β

þ β

þþβ

where f is the link function. The other components of such models are a speciﬁcation of the

form of the variance of the response variable and of its probability distribution (some

member of the

exponential family

). Particular types of model arise from this general

formulation by specifying the appropriate link function, variance and distribution. For

example, multiple regression corresponds to an identity link function, constant variance

and a normal distribution.

Logistic regression

arises from a

logit

link function and a

binomial

distribution

; here the variance of the response is related to its mean as,

variance ¼ meanð1 ðmean=nÞÞ where n is the number of observations. A dispersion

parameter (often also known as a scale factor), can also be introduced to allow for a

phenomenon such as

overdispersion

. For example, if the variance is greater than would be

expected from a binomial distribution then it could be speciﬁed as meanð1 ðmean=nÞÞ.

In most applications of such models the scaling factor, , will be one. Estimates of the

parameters in such models are generally found by

maximum likelihood estimation

. See also

GLIM, generalized additive models and generalized estimating equations. [GLM]

[Generalized Latent Variable Modeling, 2004, A. Skrondal, S. Rabe-Hesketh, Chapman

and Hall/CRC Press, Boca Raton.]

Generalized method of moments (GMM): An estimation method popular in

econometrics

that generalizes the

method of moments

estimator. Essentially the same as what is known as

estimating functions

in statistics. The

maximum likelihood estimator

and the

instrumental

variables estimator

are special cases. [Generalized Method of Moments, 2005, A. R. Hall,

Oxford University Press, Oxford]

Generalized multi nomial distri bution: The joint distribution of n discrete variables

; x

; ...; x

each having the same

marginal distribution

Prðx ¼ jÞ¼p

ðj ¼ 0; 1; 2; ...; kÞ

and such that the correlation between two different xs has a speciﬁed value .[Journal of the

Royal Statistical Society, Series B, 1962, 24, 530–4.]

184

Genera l ized odds ratio: Synonym for Agresti’s α.

Generalized p-values: A procedure introduced to deal with those situations where it is difﬁcult to

derive a signiﬁcance test because of the presence of

nuisance parameters

. The central idea is

to construct an appropriate generalized

test statistics

and to deﬁne an extreme region

consisting of all random samples for the testing problem that are as extreme as the observed

sample. Some general conditions are assumed satisﬁed, in particular that the generalized

test statistic is free of nuisance parameters. Given the observed sample the generalized

p-value is deﬁned to be the largest probability that a sample is in the extreme region under

the null hypothesis. The procedure has been shown to provide small sample solutions for

many hypothesis testing problems. [Journal of the American Statistical Association , 1989,

84, 602–607.]

Generalized Poisson distribution: A probability distribution deﬁned as follows:

PrðX ¼ 0Þ¼e

l

ð1 þlÞ

PrðX ¼ 1Þ¼le

l

ð1 Þ

PrðX ¼ xÞ¼

l

ðx  2Þ

The distribution corresponds to a situation in which values of a random variable with a

Poisson distribution

are recorded correctly, except when the true value is unity, when there is

a non-zero probability that it will be recorded as zero. [Communication in Statistics: Theory

and Methods, 1984, 10, 977–991.]

Generalized principal components analysis: A non-linear version of

principal components

analysis

in which the aim is to determine the non-linear coordinate system that is most in

agreement with the data conﬁguration. For example, for

bivariate data

, y

, if a quadratic

coordinate system is sought, then as a ﬁrst step, a variable z is deﬁned as follows:

z ¼ ay

þ by

þ cy

þ dy

þ ey

with the coefﬁcients being found so that the variance of z is a maximum among all such

quadratic functions of y

and y

.[Methods of Statistical Data Analysis of Multivariate

Observations, R. Gnanadesikan, 2nd edition, 1997, Wiley, New York.]

Genera l ized Procrustes analysis: See Procrustes analysis.

Generalized variance: See moments of the generalized variance.

Genetic algorithms: Optimization procedures motivated by biological analogies. The primary idea

is to try to mimic the ‘survival of the ﬁttest’ rule of genetic mutation in the development of

optimization algorithms. The process begins with a population of potential solutions to a

problem and a way of measuring the ﬁtness or value of each solution. A new generation of

solutions is then produced by allowing existing solutions to ‘mutate’ (change a little) or cross

over (two solutions combine to produce a new solution with aspects of both). The aim is to

produce new generations of solutions that have higher values. [IMA Journal of Mathematics

Applied in Business and Industry, 1997, 8, 323–46.]

Genetic epidemiol ogy: A science that deals with etiology, distribution, and control of disease in

groups of relatives and with inherited causes of disease in populations. [Outline of Genetic

Epidemiology, 1982, N. E. Morton, Karger, New York.]

Genetic heritabil ity: The proportion of the trait variance that is due to genetic variation in a

population. [Statistics in Human Genetics, 1998, P. Sham, Arnold, London.]

185

Genomics: The study of the structure, fuction and evolution of the deoxyribonucleic acid (DNA) or

ribonucleic acid (RNA) sequences that comprise the genome of living organisms. Genomics

is closely related (and almost synoynmous) to genetics; the former is more directly concerned

with DNA structure, function and evolution whereas the latter emphasizes the consequences

of genetic transmission for the distribution of heritable traits in families and in populations.

Genotype: The set of

alleles

present at one or more loci in an individual. [Statistics in Human

Genetics, 1998, P. Sham, Arnold, London.]

Genotypic assortment: See assortative mating.

GENSTAT: A general purpose piece of statistical software for the management and analysis of data.

The package incorporates a wide variety of data handling procedures and a wide range of

statistical techniques including, regression analysis,

cluster analysis

, and

principal compo-

nents analysis

. Its use as a sophisticated statistical programming language enables non-

standard methods of analysis to be implemented relatively easily. [http://www.vsni.co.uk.]

Geographical analysis machi ne: A procedure designed to detect clusters of rare diseases in a

particular region. Circles of ﬁxed radii are created at each point of a square grid covering the

study region. Neighbouring circles are allowed to overlap to some ﬁxed extent and the

number of cases of the disease within each circle counted. Signiﬁcance tests are then

performed based on the total number of cases and on the number of individuals at risk,

both in total and in the circle in question, during a particular census year. See also scan

statistic.[Statistics in Medicine, 1996, 15, 1961–78.]

Geographical correlations: The correlations between variables measured as averages over geo-

graphical units. See also ecological fallacy.[Environmental Research, 2003, 92,78–84.]

Geographical information system (GIS ): Software and hardware conﬁgurations through

which digital georeferences are processed and displayed. Used to identify the geographic or

spatial location of any known disease outbreak and, over time, follow its movements as well

as changes in

incidence

and

prevalence

.[Computers and Geoscience, 1997, 23,371–85.]

Geometric distribution: The probability distribution of number of trials (N) before the ﬁrst

success in a sequence of

Bernoulli trials

. Speciﬁcally the distribution is given by

PrðN ¼ nÞ¼pð1  pÞ

n1

; n ¼ 1; 2; ...

where p is the probability of a success on each trial. The mean, variance,

skewness

and

kurtosis

of the distribution are as follows:

mean ¼ 1=p

variance ¼ð1  pÞ=p

skewness ¼ð2  pÞ=ð1 pÞ

kurtosis ¼ 9 þp

=ð1 pÞ

[STD Chapter 19.]

Geometric mean: A measure of location, g, calculated from a set of observations x

; x

; ...; x

g ¼

j¼1

The geometric mean is always less than or equal to the arithmetic mean. [SMR Chapter 3 .]

186

Geostatistics: A body of methods useful for understanding and modelling the spatial variability in a

process of interest. Central to these methods is the idea that measurements taken at locations

close together tend to be more alike than values observed at locations farther apart. See also

kriging and variogram.[Practical Geostatistics, 1979, I. Clark, Applied Science, London.]

G-estimator: Estimator for causal effects, for instance in

structural nested models

, based on the

notion of potential outcomes (see

Neyman-Rubin causal framework

). Can be viewed as a

generalization of

standardization

.[Epidemiology, 1992, 3, 319–336.]

GGobi: Free software for interactive and dynamic graphics that can be operated using a command line

interface or from a graphical user interface. [Computational Statistics and Data Analysis,

2003, 43, 423–444.]

Gibbs sampling: See Markov chain Monte Carlo methods.

Gini concentration: A measure of spread, V

(X), for a variable X taking k categorical values and

deﬁned as

ðX Þ¼

i¼1

ð1 p

where p

¼ PrðX ¼ iÞ; i ¼ 1; ...; k. The statistic takes its minimum value of zero when X is

least spread, i.e., when Pr(X = j)=1 for some category j, and its maximum value (k - 1)/k when

X is most spread, i.e., when Pr(X = i)=1/k for all i.[Statistical Analysis of Categorical Data,

1999, C. J. Lloyd, Wiley, New York.]

Gini, Corrado (18 8 4^1965): Born in a small town in the region of Veneto, Italy, Gini studied

jurisprudence at the University of Bologna before becoming interested in statistics.

His thesis for his degree became, in 1908, t he ﬁrst of his eighty books, Il sesso dal

punto di vis ta statist ico. At the age of 26 Gini was already a university professor and

throughout his life held chairs in the Univers ities of Cagliari, Padua and Rome. Founded

two journals Genus and Metron and wrote over a thousand scientiﬁc papers in the areas of

probability, demography and biometry. Elected an Hona rary Fellow of the Royal

Statis tical Society in 1920, Gini was also a member of the Academia dei Lincei. He died

on 13 March 1965.

Gini index : See Lorenz curve.

GIS: Abbreviation for geographical information system.

Gittins indices: Synonym for dynamic allocation indices.

Glejser test: A test for heteroscedasticity in the error terms of a regression analysis that involves

regressing the absolute values of regression residuals for the sample on the values of the

independent variable thought to covary with the variance of the error terms. See also

Goldﬁeld–Quandt test.[Regression Analysis, Volume 2, ed. M. S. Lewis-Beck, Sage

Publications, London.]

GLIM: A software package particularly suited for ﬁtting

generalized linear models

(the acronym stands

for Generalized Linear Interactive Modelling), including

log-linear models

logistic models

and models based on the

complementary log-log transformation

. A large number of GLIM

macros are now available that can be used for a variety of non-standard statistical analyses.

[NAG Ltd, Wilkinson House, Jordan Hill Road, Oxford OX2 8DR, UK; NAG Inc., 1400

Opus Place, Suite 200, Downers Grove, Illinois 60515-5702, USA.]

187

G l ivenko-Cantel li theorem: A theorem stating that the empirical distribution function for a

random variable x converges, for all x, almost surely to the true distribution function as

the number of independent identically distributed observations increases. [Annals of

Probability, 1987, 15, 837–870.]

GLL AMM: A program that estimates generalized linear latent and mixed models by maximum like-

lihood. The models that can be ﬁtted include

multi-level models

structural equation models

and

latent class models

. The response variables can be of mixed types including continuous,

counts, survival times, dichotomous, and ordinal. [Details and manuals available at http://

www.gllamm.org/]

GLM: Abbrevation for generalized linear model.

GLMM: Abbreviation for generalized linear mixed models.

GLS: Abbreviation for generalized least squares.

Glyphs: A general term for the graphics that are sometimes used to represent multivariate observations.

Two examples are

Chernoff faces

and

snowﬂakes

Gnedenko, Boris (1 91 2^1995): Born on 1 January 1912 in Simbirsk a town on the River Volga,

Gnedenko studied at the University of Saratov. In 1934 he joined the Institute of

Mathematics at Moscow State University and studied under Khinchin and later

Kolmogorov. In 1938 he became associate professor in the Department of Mechanics

and Mathematics. Gnedenko’s main work was on various aspects of theoretical statistics

particularly the limiting distribution of maxima of independent and identically distributed

random variables. The ﬁrst edition of what is widely regarded as his most important

published work, Limit Distributions for Sums of Independent Random Variables appeared

in 1949. In 1951 Gnedenko published The Theory of Probability which remained a

popular account of the topic for students for over a decade. Later in his career

Gnedenko took an interest in

reliability theory

and

quality control procedures

and

played a role in the modernization of Soviet industry including the space programme.

He also devoted much time to popularizing mathematics. Gnedenko died in Moscow on

27 December 1995.

Goelles, Josef (1929^2000): Goelles studied mathematics, physics and psychology at the

University of Graz, and received a Ph.D in mathematics in 1964. He began his scientiﬁc

career at the Technical University of Graz and in 1985 founded the Institute of Applied

Statistics and Systems Analysis at Joanneum Research and chaired it until shortly before his

death. He collaborated in a large number of joint projects with clinicians and biologists and

tried hard to convince other colleagues to incorporate statistical reasoning into their own

discipline.

Golden ^ Thompson inequality: An inequality relating to the

matrix exponential transformation

and given by

trace½expðAÞexpðBÞ  trace½expðA þ BÞ

with equality if and only if A and B commute. [Linear Algebra and its Applications, 1996,

243, 105–12.]

Goldfeld^ Quandt test: A test for heteroscedastic ity in the error terms of a regression analysis that

involves examining the monotonic relationship between an explanatory variable and the variance

oftheerrorterm.SeealsoGlejser test.[Review of Agricultural Economics, 2000, 22, 421–37.]

188