Епифанов В.Н. Краткий курс метрологии, стандартизации и сертификации
Подождите немного. Документ загружается.


31
Эти, а также системы измерений количества топлива в баках строительных
машин, температуры в печах обжига кирпича, скорости движения лент и нагрузки
на ленты конвейеров на бетонных заводах и другие изучаются студентами на
практических занятиях.
Особым средством измерений является эталон.
Эталон – это высокоточная мера, предназначенная для воспроизведения и хра-
нения единицы величины с целью передачи ее размера другим средствам измере-
ний. От эталона единица величины передается разрядным эталонам, а от них – ра-
бочим средствам измерений.
Эталоны классифицируют на первичные, вторичные и рабочие.
Первичный эталон – это эталон, воспроизводящий единицу физической вели-
чины с наивысшей точностью, возможной в данной области измерений на совре-
менном этапе научно-технических достижений. Первичный эталон может быть на-
циональным (государственным) и международным. В России первичные эталоны
утверждает Госстандарт РФ.
Вторичные эталоны («эталоны-копии») – воспринимают размер единицы от
государственного эталона.
Рабочие эталоны воспринимают размер единицы от вторичных эталонов и
служат для передачи размера менее точному рабочему эталону и рабочим средствам
измерений.
За последние годы получены высокие результаты точности и надежности этало-
нов, создаваемых на основе использования квантовых эффектов. С использованием
квантовых эффектов были созданы современные эталоны ампера, ома, метра.
Ученые полагают, что квантовые эталоны можно будет считать «вечными мера-
ми», так как способность воспроизведения единиц физических величин у таких эта-
лонов не подвержена влиянию внешних условий, географического местонахождения
и времени.
2.5. Погрешности измерений
Результаты измерения физической величины дают лишь приближенное ее зна-
чение. Отклонение результата измерения от действительного (истинного) значения
измеряемой величины называют погрешностью измерения.
Погрешности измерений имеют систематическую и случайную составляющие,
которые также называют систематическими и случайными погрешностями.
Под систематическими погрешностями понимают, погрешности остающиеся
постоянными или изменяющимися по определенному закону при повторных измере-
ниях одной и той же величины. Систематические погрешности могут быть опреде-
лены и устранены путем введения соответствующих поправок, например, погреш-
ность градуировки шкалы измерительного прибора.
Систематические погрешности можно разделить на группы, отличающиеся од-
на от другой причинами возникновения: инструментальные погрешности; погрешно-
сти метода измерений (методические); погрешности возникающие вследствие внеш-
них влияний (температуры воздуха, магнитных полей и т.д.).

32
Инструментальными называются погрешности, причина которых заключается в
свойствах применяемых средств измерений (особенности конструкции, несовершен-
ство технологии изготовления, износ, старение).
Методические погрешности являются следствием тех или иных допущений или
упрощений при определении измеряемой величины (например, из-за того, что не
учитывается потребление мощности средствами измерений.)
Случайными называются погрешности, изменяющиеся случайным образом при
повторных измерениях одной и той же величины. Случайные погрешности нельзя
исключить опытным путем. Они происходят от влияния на результат измерения
причин случайного характера. Наличие случайных погрешностей выявляется при
проведении ряда равноточных измерений одной и той же величины, когда оказыва-
ется, что результаты измерений не совпадают друг с другом.
Равноточные измерения – это ряд измерений какой-либо величины, выполнен-
ных одинаковыми по точности средствами измерений в одних и тех же условиях с
одинаковой тщательностью.
Грубые погрешности (промахи) – это погрешности, значительно превышающие
погрешности результатов других измерений, выполненных при тех же контроли-
руемых условиях. Причиной этого может быть ошибка оператора, возникновение
сильной кратковременной помехи, толчок, нарушение электрического контакта и
т.п. Промахи необходимо выявить, исключить и не учитывать при дальнейшей ста-
тистической обработке результатов измерений.
По способу числового выражения различают погрешности абсолютные и от-
носительные.
Абсолютная погрешность измерения
д
хх
−
=
∆
,
где – измеренное значение; – действительное значение измеряемой величины, х
д
х
которое находится по показанию эталонного прибора или путем статистической об-
работки ряда результатов равноточных измерений.
Абсолютная погрешность выражается в единицах измеренной величины. Аб-
солютная погрешность, взятая с обратным знаком, называется поправкой П:
∆
−
=
П
.
Относительная погрешность измерения
д
х
∆
=
δ
, или в процентах 100⋅
∆
=
д
х
δ
.

33
При практических измерениях чаще всего неизвестно. В этом случае отно-
д
х
сительная погрешность определяется по измеренному значению .
изм
х
100⋅
∆
=
изм
х
δ
.
2.5.1. Способы исключения систематических погрешностей
1) Инструментальные систематические погрешности обычно выявляют по-
средством поверки средства измерения. При поверке показания поверяемого при-
бора сравниваются с показаниями образцового средства измерения. Вводится по-
правка, равная обнаруженной погрешности с обратным знаком.
2) Метод замещения – это метод сравнения с мерой, по которому измеряемая
величина заменяется в измерительной установке известной величиной, воспроизво-
димой мерой, причем путем изменения известной величины измерительная установ-
ка приводится в прежнее состояние, т.е. достигаются те же показания приборов, что
и при действии измеряемой величины.
3) Метод компенсации погрешности по знаку. Этот метод применяют для ис-
ключения известных по природе, но не известных по значению погрешностей, ис-
точники которых имеют направленное действие (например, постоянные магнитные
поля, термо-ЭДС и т.п). Для устранения таких погрешностей измерения производят
дважды так, чтобы погрешность входила в результаты измерений с противополож-
ными знаками. В качестве окончательного результата принимают среднее арифме-
тическое значение результатов двух измерений.
4) Методические систематические погрешности устраняются уточнением ме-
тодики измерений. Например, для уточнения измерения площади прямоугольника
нужно кроме измерения сторон проверить равенство диагоналей и ввести поправку
в расчет, если они не равны.
2.5.2. Возникновение случайных погрешностей
Причины возникновения случайных погрешностей очевидны:
- неисправное состояние в результате старения средств измерений, например,
из-за возникновения чрезмерного трения в опорах измерительного прибора;
- влияние случайных внешних воздействий в виде ухудшения освещенности,
возникновения шума или вибрации от случайных внешних источников;
- недостаточная квалификация или плохое самочувствие персонала испытате-
лей.
Примером субъективных случайных погрешностей может быть непонимание
испытателем явления параллакса. Параллакс – это кажущееся изменение положе-
ния предмета в пространстве в зависимости от положения глаза наблюдателя.
Особенно часто случайная погрешность измерений из-за параллакса возникает
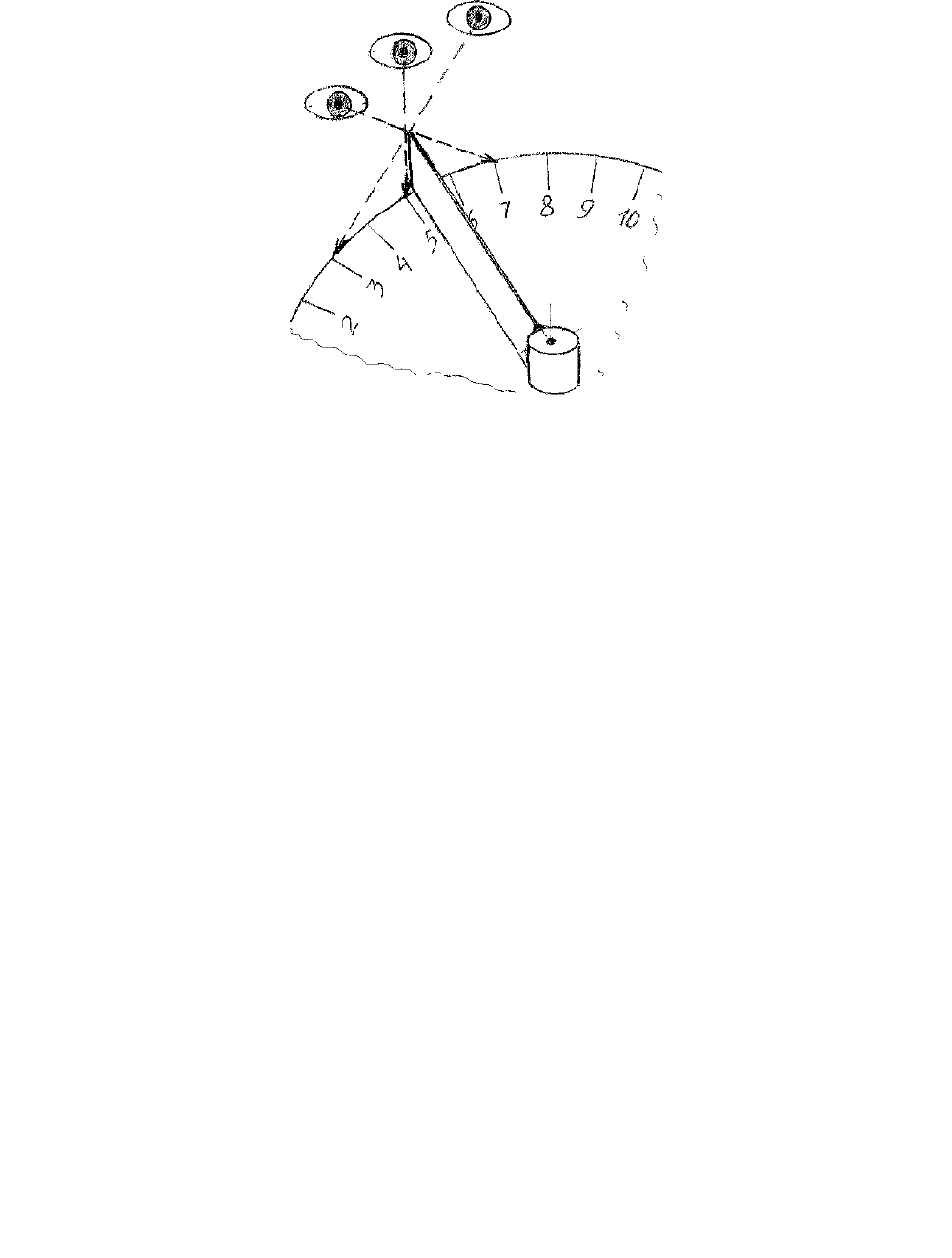
при использовании стрелочных указателей. Суть возникновения случайной по-
грешности видна из рис. 5.
34
Рис. 5
Если глаз наблюдателя расположен правильно над стрелкой прибора, то де-
лается отсчет размера измеряемой величины 5, если справа от стрелки, то опреде-
ляется размер 3, а если слева, то размер 7.
Из сказанного очевидно, что исключить случайные погрешности измерений
введением поправок, как для систематических погрешностей, невозможно. Ко-
нечно, уменьшить вероятность их возникновения можно путем содержания
средств измерения в исправном состоянии, улучшения условий проведения изме-
рений, повышением уровня ответственности и квалификации испытателей.
Тем не менее, единственным надежным методом устранения их влияния яв-
ляются многократные измерения и обработка результатов многократных измере-
ний методами теории вероятностей.
Изложенный ниже метод оценки случайных погрешностей и обработки ре-
зультатов ограниченного числа измерений широко применяется при оценке каче-
ства строительных материалов и конструкций.
Так, при использовании механических методов неразрушающего контроля
прочности бетона в ГОСТ 22690-88 изложены требования к многократности из-
мерений и последующей обработке результатов. Заметим, что в соответствии с
законом «О техническом регулировании», вступившем в силу с 1 июля 2003 г.,
требования ГОСТ остаются в силе в течение семилетнего срока. Многократные
испытания предусмотрены при контроле прочности бетона пружинным молотком
ПМ, универсальным маятниковым прибором УМП, маятниковым дисковым при-
бором ДПГ-4, прибором ОНИКС (упругий отскок). Более того, современные при-
боры ОНИКС-2,4 имеют цифровую индексацию показаний и автоматическую об-
работку информации, полученной при многократных измерениях.

35
2.5.3. Оценка случайных погрешностей и обработка
результатов многократных измерений
Факторы, определяющие возникновение случайных погрешностей, проявля-
ются нерегулярно, в различных комбинациях и с интенсивностью, которую труд-
но предвидеть. Случайная погрешность случайно изменяется при повторных из-
мерениях одной и той же физической величины. Однако если оперировать ис-
правленными результатами измерений, т. е. такими, из которых исключены сис-
тематические погрешности, то чисто случайные погрешности будут обладать сле-
дующими свойствами:
• равные по абсолютной величине положительные и отрицательные погреш-
ности равновероятны;
• большие погрешности наблюдаются реже, чем малые;
• с увеличением числа измерений одной и той же величины среднее арифме-
тическое погрешностей стремится к нулю, и, следовательно, среднее арифметиче-
ское результатов измерений стремится к истинному значению измеряемой вели-
чины.
Наиболее универсальный способ описания случайных величин заключается в
отыскании их интегральных или дифференциальных функций распределения.
В реальных условиях производства может быть выполнено только ограни-
ченное число (10…20, не более) измерений. По их результатам определить дейст-
вительное значение измеряемой величины невозможно. Однако даже ограничен-
ное число измерений дает возможность путем расчета оценить интервал, в кото-
ром должно находиться действительное значение. Причем эта оценка может быть
сделана с очень высокой доверительной вероятностью. Например, доверительная
вероятность оценки 0,999 означает, что ошибка в расчетах не превышает 0,1 %.
Для осуществления таких расчетов используется математический аппарат
теории вероятностей, которая является наукой о закономерностях случайных со-
бытий, в том числе и случайных погрешностей измерений.
Теоретически доказано, что распределение случайных погрешностей близко
к нормальному. Это видно и из приведенных выше свойств этих погрешностей.
Плотность нормального распределения вероятностей для случайной величи-
ны (рис. 6 а) описывается уравнением
2
2
2
)(
2
1
)(
σ
πσ
x
mх
еxр
−
= ,
где и
х
m
σ
– математическое ожидание и среднее квадратическое отклонение, яв-
ляющиеся основными параметрами нормального распределения; е – основание на-
турального логарифма.
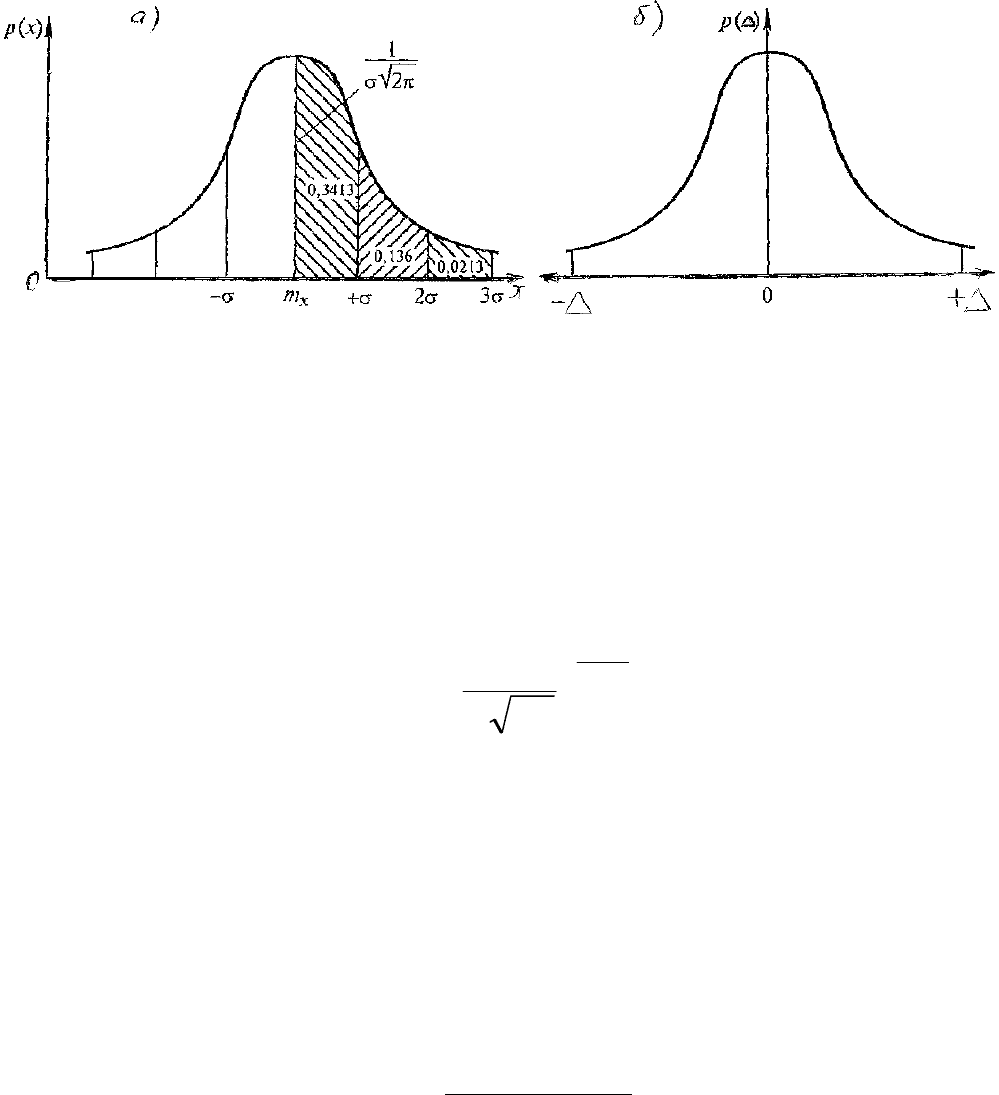
36
Рис. 6
Кривая имеет точки перегиба, соответствующие абсциссам
σ
±
х
m .
Если данную кривую рассматривают как плотность распределения случайных
погрешностей , то начало координат переносят в центр распределения и по оси ∆
абсцисс откладывают значения погрешностей
х
mх
−
=
∆
(рис. 6 б). Уравнение при-
нимает вид
2
2
2
2
1
)(
σ
πσ
∆
=∆ ер .
На практике приходится довольствоваться ограниченным числом измерений
для того, чтобы оценить действительное значение измеряемой величины и досто-
верность этой оценки. Пусть получен ряд значений измеряемой величины
х
1
,
х
2
,…,х
n
, где n – число измерений.
Если принять, что систематические погрешности устранены описанными ра-
нее методами и мы имеем дело только со случайными погрешностями, то наибо-
лее достоверное значение измеряемой величины есть среднее арифметическое по-
лученных значений измерений
n
ххх
ср
х
n
+
+
+
=
...
21
.
Абсолютные случайные погрешности составят:
ср
хх
−
=
∆
11
,
ср
хх
−
=
∆
2
2
,
----------------------
ср
x
n
x
n
−
=
∆
.

37
Так как предполагается, что распределение погрешностей нормальное, то они
должны иметь и положительные, и отрицательные значения.
Средняя квадратическая погрешность определяется по формуле
1
...
22
2
2
1
−
∆+∆+∆
=
n
n
σ
.
В процессе измерений возможны грубые ошибки, которые не должны повли-
ять на оценку действительного значения измеряемой величины. По правилу «трех
сигм» погрешности |∆
i
| > 3σ считаются промахами и при обработке результатов
измерений не учитываются. После исключения из ряда измерений промахов рас-
чет повторяют для нового значения
n.
Как указывалось ранее, среднее арифметическое
х
ср
ряда измерений явля-
ется только наиболее достоверным, но не точным значением измеряемой вели-
чины. Точность результата измерения
х
ср
оценивается с помощью средней квад-
ратической погрешности среднего арифметического значения х
ср
n
S
σ
= .
Из данного выражения видно, что увеличение количества п повторных из-
мерений приводит к уменьшению средней квадратической погрешности S резуль-
тата измерений.
Интервал, за границы которого погрешность не выходит с некоторой вероят-
ностью, называется доверительным интервалом, а характеризующая его вероят-
ность доверительной вероятностью.
Указанный способ определения доверительных интервалов справедлив
только при n > 100. Так, при числе измерений n = 10…20 доверительная вероят-
ность оценки составит только р = 0,65. Такая достоверность расчета не пригодна
для проектирования и оценки качества строительных работ. Если вернуться к не-
разрушающим методам контроля качества бетона, то определить, что бетон соот-
ветствует некоторой марке, и гарантировать это только на 65 % – значит вообще
ничего не определить. Можно было никаких испытаний и не проводить. Нужна
доверительная вероятность не ниже 0,98. Для определения доверительного ин-
тервала с высокой доверительной вероятностью нужно пользоваться коэффици-
ентами Стьюдента t (n, p), которые зависят от требуемой доверительной вероят-
ности р и количества измерений n (табл. 7).

38
Таблица 7
Коэффициенты Стьюдента
Доверительная вероятность р n
0,5 0,6 0,7 0,8 0,9 0,95 0,98 0,99 0,999
2 1,00 1,38 2,0 3,1 6,3 12,7 31,8 63,7 636,6
3 0,82 1,06 1,3 1,9 2,6 4,3 7,0 9,9 31,6
4 0,77 0,98 1,3 1,6 2,4 3,2 4,5 5,8 12,9
5 0,74 0,94 1,2 1,5 2,1 2,8 3,7 4,6 8,6
6 0,73 0,92 1,2 1,4 2,0 2,6 3,4 4,0 6,9
7 0,72 0,90 1,2 1,4 1,9 2,4 3,1 3,7 6,0
8 0,71 0,90 1,1 1,4 1,9 2,4 3,0 3,5 5,4
9 0,71 0,90 1,1 1,4 1,9 2,3 2,9 3,4 5,0
10 0,70 0,88 1,1 1,4 1,8 2,3 2,8 3,3 4,8
15 0,69 0,87 1,1 1,3 1,8 2,1 2,6 3,0 4,1
20 0,69 0,86 1,1 1,3 1,7 2,1 2,5 2,9 3,9
30 0,68 0,85 1,1 1,3 1,7 2,0 2,5 2,8 3,7
Зная S, п, p, определяют доверительный интервал х∆
±
, в который с за-
данной вероятностью р и при количестве измерений п входит действительное
значение измеряемой величины :
д
х
⋅
=
∆
pntSх , .
Окончательный результат измерения записывают так:
ххх
срд
∆
±
=
.
Для экспериментального определения закона распределения погрешностей
строится гистограмма – ступенчатая кривая
(рис. 7). Термин гистограмма
происходит от греческого histos – столб. Для ее построения полученный статиче-
ский ряд погрешностей
)(
/
∆n
n
∆
∆∆ ,...,,
21
делят на несколько равных интервалов шири-
ной
. На рис. 7 таких интервалов восемь. Далее подсчитывают сколько значений
погрешностей из ряда
/
∆
/
i
n
n
∆
∆∆ ,...,,
21
попадают в каждый из интервалов, по оси ор-
динат откладывают эти значения и строят столбики. На рис. 7 первый интервал
попало одно значение погрешности
в
(
)
1
/
1
=
n , во второй – два
(
)
2
/
2
=
n , в третий –
пять
(
)
5
/
3
=
n и т. д. Статическая функция распределения р(
∆
) строится по точкам,
проходящим через середины вершин столбиков. Значения ординат точек этой
кривой имеют смысл вероятности попадания в данный интервал
n
n
i
/
р
i
= , где n –
общее число измерений;
i – номер интервала.
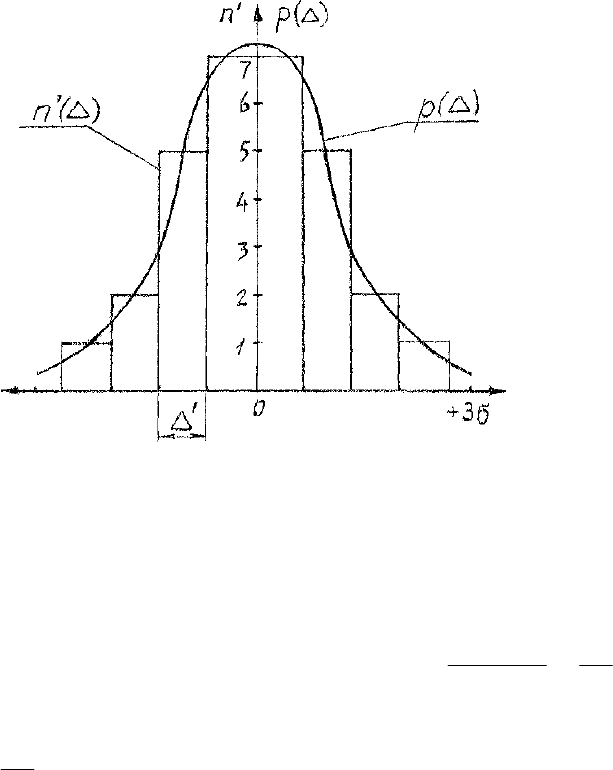
39
Рис. 7
Если принять площадь
S
общ
всей гистограммы за единицу, то площадь каж-
дого столбика S
i
в долях от S
общ
равна вероятности попадания погрешности в
i-й интервал. Действительно, так как основания всех столбиков одинаковы (они
равны
), а , то S
/
∆ n
i
n =∑
/
i
как доля от S
общ
равна
n
n
n
n
S
i
i
i
i
/
//
//
=
∑∆
∆
= . Выше по-
казано, что и
n
n
р
i
i
/
= . На рис. 6а приведены вероятности попадания значений
случайных величин при нормальном распределении в интервалы 0…
σ
,
σ
…2
σ
,
2
σ
…3
σ
.
Подробная методика и пример решения задачи оценки действительного зна-
чения физической величины по ряду измерений приведены в методических указа-
ниях по контрольной работе для студентов-заочников.
2.6. Метрологические характеристики и классы точности
средств измерений
Характеристики свойств средств измерений, оказывающих влияние на ре-
зультаты измерений и возникающие при этом погрешности, называются метроло-
гическими характеристиками средств измерений.
Характеристики, указанные в НТД, называются нормированным, а опреде-
ляемые экспериментально – действительными.
Нормирование метрологических характеристик позволяет правильно выби-
рать измерительные средства и формировать измерительные системы, правильно
оценивать погрешности измерений.
В строительстве используют рабочие средства измерений, метрологические
характеристики которых нормированы на основе классов точности.

40
Класс точности – обобщенная характеристика средств измерений опреде-
ленного типа, позволяющая судить о том, в каком диапазоне находится суммарная
погрешность измерений. Общие требования при делении средств измерений на
классы точности приведены в ГОСТ 8.401-80 «Классы точности средств измере-
ний. Общие требования».
Обозначения классов точности наносятся на циферблаты, щитки и корпуса
средств измерений.
Обозначения могут иметь форму заглавных букв латинского алфавита или
римских цифр с добавлением условных знаков. Смысл таких обозначений рас-
крывается в НТД. Если класс точности обозначается арабскими цифрами с допол-
нительным знаком, то эти цифры оценивают погрешность измерения.
Например, для гирь, штангенинструмента, концевых мер длины указывают
значения абсолютных погрешностей
∆
, класс точности обозначается одной араб-
ской цифрой: 0; 1; 2. Наименьшие погрешности соответствуют классу 0. Значения
этих погрешностей указаны в стандартах.
Если нормируется предельная относительная погрешность
δ
, то класс точ-
ности обозначается в виде 1,0 , где 1,0 – значение предельной относительной по-
грешности в процентах от измеренного значения. Например, при выполнении из-
мерения прибором, имеющим на щитке обозначение 1,5 , получен результат 200.
Тогда по известному выражению (см. стр. 32)
100⋅
∆
=
изм
х
δ
вычисляем абсо-
лютную предельную погрешность измерения
3
100
2005,1
100
===∆
⋅⋅
изм
х
δ
.
Это означает, что измеренное значение находится в интервале 200 ± 3.
Для многих приборов, например вольтметров, амперметров, нормируют зна-
чение приведенной погрешности
γ
, измеряемой в процентах:
100
N
х
∆
=
γ
,
где х
N
– значение верхнего предела измерений.
Класс точности при этом обозначается числом, как и при нормировании от-
носительной погрешности, но дополнительного значка при этом нет. Например,
если вольтметр класса 1,5 с диапазоном измерений от 0 до 250 В показывает на-
пряжение 36 В, то абсолютная погрешность измерения, В, составит:
∆ =250·0,015=
= 3,75, а относительная погрешность измерения, %, составит:
δ
= 3,75 : 36·100 =
=10. Для приборов с нормируемой приведенной погрешностью абсолютная по-
грешность не зависит от значения измеряемой величины, а относительная по-
грешность увеличивается с уменьшением значения измеряемой величины. Значе-
ние абсолютной погрешности можно снизить, если использовать прибор того же
класса точности, но с меньшим диапазоном измерений.
