Emmrich E., Wittbold P. (editors) Analytical and Numerical Aspects of Partial Differential Equations: Notes of a Lecture Series
Подождите немного. Документ загружается.


Standing waves in nonlinear Schrödinger equations 1
65
Now, we remark that, since by (3.3) any solution v o
f (3.1) satisfies I(v) = 0, we have
d 6 m. (3.26)
Since ϕ
ω
is a solution of (3.1), it follows from the definition of the least energy level
m (see (3.20)) that
m 6 S(ϕ
ω
). (3.27)
Combining (3.24)–(3.27) gives
S(ϕ
ω
) = c = d = m
and completes the proof.
Remark 3.14. F
or more general nonlinearities, the equality m = c between the moun-
tain pass level and the least energy level still holds (see [41, 42]).
3.4 Uniqueness
It turns out that we are able to describe explicitly the set G of ground states (see (3.21)).
Theorem 3.15. There exists a real-valued, positive, spherically symmetric and de-
creasing function Ψ ∈ H
1
(R
N
) such that
G = {e
iθ
Ψ(·− y);θ ∈ R, y ∈ R
N
}.
Therefore, the ground state is unique up to translations and phase shifts. It would
exceed the scope of these notes to give a proof of Theorem 3.15 and we just indicate
some references. First, a simple and general proof that any complex-valued ground
state ϕ is of the form e
iθ
˜ϕ with θ ∈ R and ˜ϕ a real positive ground state was recently
given in [16] (see also [36]). The fact that all real positive ground states of (3.1) are
radial up to translations was first proved by Gidas, Ni and Nirenberg in 1979 (see [29])
by using the so-called moving planes method. Alternatively, the same result can be
deduced by the method of Lopes [54], which relies on symmetrizations with respect to
suitably chosen hyperplanes combined with a unique continuation theorem. Recently,
Maris [55] developed for the symmetry of minimizers for a large class of problems a
new method that furnishes a simpler proof of radial symmetry of real ground states, see
[12], without even assuming a priori that they are positive. Uniqueness follows from a
result of Kwong [47] in 1989.
Remark 3.16. When N = 1, it turns out that the set of all solutions of (3.1) (not only
those of least energy) is precisely the set of ground states
G = {e
iθ
Ψ(· −y);θ ∈ R, y ∈ R
N
} = {v;v is a solution of (3.1) }.
Moreover, we are able to give an explicit formula for Ψ,
Ψ(x) =
(p + 1)ω
2
sech
2
(p −1)
√
ω
2
x
1
p−1
.
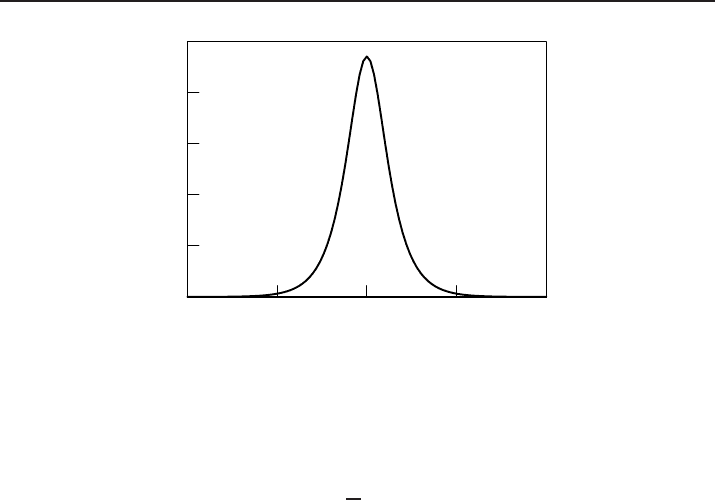
F
or p = 3 and ω = 1, the shape of Ψ is given in Figure 4.
In higher dimensions, it is known that there exist solutions of (3.1) that are not
ground states (see [8, 10, 52]), and no explicit solution is available.
166 S
tefan Le Coz
0.3
0.6
0.9
1.2
1.5
−1
0 −5 0 5 10
Figure 4. The function Ψ for N = 1, p = 3 and ω = 1.
4 Stability
In this section, we will prove that for ϕ ∈ G the standing wave e
iωt
ϕ(x) is stable (in a
sense to be made precise) if 1 < p < 1 +
4
N
.
I
n his report [67] of 1844, Russel was already mentioning the observed remarkable
stability properties of solitary waves. From the mathematical point of view, the concept
of stability that comes naturally in mind for the standing waves e
iωt
ϕ(x) of (1.1) is
stability in the sense of Lyapunov, which means uniformly continuous dependence on
the initial data: For all ε > 0 there exists δ > 0 such that for all u
0
∈ H
1
(R
N
),
ku
0
− ϕk
H
1
(R
N
)
< δ =⇒ ku(t) − e
iωt
ϕk
H
1
(R
N
)
< ε for all t,
where u is the maximal solution of (1.1) with u(0) = u
0
. However, with this definition,
all standing waves would be unstable (see Remark 4.2), which is contradictory with
what is observed for such phenomena. Therefore, we have to look for a different notion
of stability.
The main reason for standing waves being unstable in the sense of Lyapunov is
that (1.1) admits translation and phase shift invariance: If u = u(t, x) is a solution of
(1.1) then for all θ ∈ R and y ∈ R
N
, e
iθ
u(·, · − y) is still a solution of (1.1). In some
sense, the equation does not prescribe the behavior of the solutions in the “direction”
of translations and phase shifts. To take this fact into account, we define the concept of
orbital stability, which is Lyapunov stability up to translations and phase shifts.
Definition 4.1. Let ϕ be a solution of (3.1). The standing wave e
iωt
ϕ(x) is said to be
orbitally stable in H
1
(R
N
) if for all ε > 0 there exists δ > 0 such that if u
0
∈ H
1
(R
N
)
satisfies ku
0
− ϕk
H
1
(R
N
)
< δ then the maximal solution u = u(t) of (1.1) with u(0) =
u
0
exists for all t ∈ R and
sup
t∈R
inf
θ∈R
inf
y∈R
N
ku(t) −e
iθ
ϕ(· − y)k
H
1
(R
N
)
< ε.
Otherwise, the standing wave is said to be unstable.

Standing waves in nonlinear Schrödinger equations 1
67
Remark 4.2. T
he concept of orbital stability is optimal in the following sense (see
[14, 15]).
•
Space translations are necessary: For a solution ϕ of (3.1), ε > 0 and y ∈ R
N
with |y| = 1, let ϕ
ε
(x) := e
iεx·y
ϕ(x). Then it is easy to check that the solution of
(1.1) with initial datum ϕ
ε
is
u
ε
(t, x) = e
iε(x·y−εt)
e
iωt
ϕ(x −2εty).
We clearly have ϕ
ε
→ ϕ in H
1
(R
N
) as ε → 0, but for any ε > 0
sup
t∈R
inf
θ∈R
ku
ε
(t) − e
iθ
ϕk
H
1
(R
N
)
= 2kϕk
H
1
(R
N
)
.
Conversely, note that if we consider (1.1) in the subspace of H
1
(R
N
) consist-
ing of radial functions then no space translation can occur and we can omit the
translations in the definition of orbital stability.
•
Phase shifts are necessary: For a solution ϕ of (3.1) and ε > 0, let ϕ
ε
(x) :=
(1 + ε)
1
p−1
ϕ(
(1 + ε)
1
2
x).
Then it is easy to check that the solution of (1.1) with
initial datum ϕ
ε
is
u
ε
(t, x) = e
iω(1+ε)t
(1 + ε)
1
p−1
ϕ(
(1 + ε)
1
2
x).
W
e clearly have ϕ
ε
→ ϕ in H
1
(R
N
) as ε → 0 but for any ε > 0
sup
t∈R
inf
y∈R
N
ku
ε
(t) − ϕ(· −y)k
H
1
(R
N
)
> kϕk
H
1
(R
N
)
.
Remark that ϕ
ε
is a solution of (3.1) with ω being replaced by ω(1 + ε).
The main result of this section is the following.
Theorem 4.3. Let ϕ be a ground state of (3.1). If 1 < p < 1 +
4
N
th
en the standing
wave e
iωt
ϕ(x) is orbitally stable.
Remark 4.4. The range of p is optimal: We will see in the next section that instability
occurs if p > 1 +
4
N
.
R
emark 4.5. Except for N = 1, where all solutions of (3.1) are ground states, The-
orem 4.3 asserts only the stability of standing waves corresponding to ground states.
It is an open problem to describe the behavior of other standing waves of (1.1) under
perturbations (see nevertheless [33, 74] and the references cited therein).
The first rigorous stability study is due to Benjamin [5] for solitary waves of the
Korteweg–de Vries equation. Roughly speaking, two different approaches are pos-
sible in the study of stability of standing waves. The first one was introduced by
Cazenave [13] and then developed by Cazenave and Lions [15]. It relies on varia-
tional and compactness arguments. The main step in this approach consists in charac-
terizing the ground states as minimizers of the energy on a sphere of L
2
(R
N
). To use

168 S
tefan Le Coz
this approach, it is essential to have a uniqueness result for ground states as Theorem
3
.15, otherwise a weaker result is obtained: stability of the set of ground states (see
Remark 4.9). The second approach was introduced by Weinstein [76, 77] (see also
[66]) and then considerably generalized by Grillakis, Shatah and Strauss [34, 35]. A
criterion based on a form of coercivity for S
′′
(ϕ) is derived in this work and allows to
prove stability of standing waves. Sufficient conditions for instability are also given in
[34, 35].
The rest of this section is devoted to the proofs of Theorem 4.3. In Subsection
4.1, we present the proof using the Cazenave–Lions method and in Subsection 4.2 we
present the proof using Grillakis–Shatah–Strauss method.
4.1 Cazenave–Lions method
The proof of Theorem 4.3 by the Cazenave–Lions method relies on the following com-
pactness result.
Proposition 4.6. Let 1 < p < 1 +
4
N
.
For any τ > 0, define
Σ
τ
:= {v ∈ H
1
(R
N
);kvk
2
L
2
(R
N
)
= τ}.
Consider the minimization problem
−ν
τ
:= inf{E(v);v ∈ Σ
τ
},
where E is the functional defined in (2.2): For v ∈ H
1
(R
N
),
E(v) =
1
2
k
∇vk
2
L
2
(R
N
)
−
1
p + 1
kvk
p+
1
L
p+1
(R
N
)
.
Then ν
τ
< +∞, and if (v
n
) ⊂ H
1
(R
N
) is such that
kv
n
k
2
L
2
(R
N
)
→ τ and E(v
n
) → −ν
τ
as n → +∞,
then there exist a sequence (y
n
) ⊂ R
N
and a function v ∈ H
1
(R
N
) such that, possibly
for a subsequence only,
v
n
(· −y
n
) → v strongly in H
1
(R
N
).
In particular, v ∈ Σ
τ
and E(v) = −ν
τ
.
The proof of Proposition 4.6 is based on the concentration-compactness principle
of Lions [50, 51]. We refer to [14, 15] for a detailed proof.
Remark 4.7. For p > 1+
4
N
, it is easy to see that ν
τ
= +∞. Indeed, let v ∈ Σ
τ
. Using
the scaled functions v
λ
(·) := λ
N
2
v(λ·), we obtain kv
λ
k
2
L
2
(R
N
)
= kvk
2
L
2
(R
N
)
= τ, but
lim
λ→+∞
E(v
λ
) = −∞. Therefore, Proposition 4.6 cannot hold in this case.
Standing waves in nonlinear Schrödinger equations 1
69
Next we characterize the ground states of (3.1) as minimizers of the energy on a
s
phere of L
2
(R
N
).
Proposition 4.8. Let 1 < p < 1 +
4
N
.
Then
(i) there exists τ
G
> 0 such that kϕk
2
L
2
(R
N
)
= τ
G
for all ϕ ∈ G,
(ii) ϕ ∈ G if and only if ϕ ∈ Σ
τ
G
and E(ϕ) = −ν
τ
G
.
Sketch of proof. Point (i) follows immediately from Theorem 3.15. We refer to [14]
for the proof of (ii).
Proof of Theorem 4.3 by the Cazenave–Lions method. T
he result is proved by contra-
diction. Assume that there exist ε > 0 and two sequences (u
n,0
) ⊂ H
1
(R
N
), (t
n
) ⊂ R
such that
ku
n,0
− ϕk
H
1
(R
N
)
→ 0 as n → +∞, (4.1)
inf
θ∈R
inf
y∈R
N
ku
n
(t
n
) −e
iθ
ϕ(· − y)k
H
1
(R
N
)
> ε for all n ∈ N, (4.2)
where u
n
is the maximal solution of (1.1) with initial datum u
n,0
. Set v
n
(x) :=
u
n
(t
n
, x). By (4.1) and the conservation of charge and energy (see (2.3)), we have,
as n → +∞,
kv
n
k
2
L
2
(R
N
)
= ku
n
(t
n
)k
2
L
2
(R
N
)
= ku
n,0
k
2
L
2
(R
N
)
→ kϕk
2
L
2
(R
N
)
= τ
G
, (4.3)
E(v
n
) = E(u
n
(t
n
)) = E(u
n,0
) → E(ϕ) = −ν
τ
G
. (4.4)
By (4.3), (4.4) and Proposition 4.6, there exist (y
n
) ⊂ R
N
and v ∈ H
1
(R
N
) such that
kv
n
(· −y
n
) −vk
H
1
(R
N
)
→ 0 as n → +∞, (4.5)
v ∈ Σ
τ
G
and E(v) = −ν
τ
G
. (4.6)
By (4.6) and Proposition 4.8, we have v ∈ G. Therefore, by Theorem 3.15, there exist
θ ∈ R and y ∈ R
N
such that v = e
iθ
ϕ(· − y). Remembering that v
n
= u
n
(t
n
) and
substituting this in (4.5), we get
ku
n
(t
n
) −e
iθ
ϕ(· − (y − y
n
))k
H
1
(R
N
)
→ 0 when n → +∞,
which is a contradiction with (4.2) and finishes the proof.
Remark 4.9. I
t is essentialfor the proofof Theorem 4.3 bythe Cazenave–Lions method
that the set of ground states G can be explicitly described by {e
iθ
Ψ(· − y);θ ∈ R, y ∈
R
N
} as in Theorem 3.15. This uniqueness result is far from being obvious even with
our simple pure power nonlinearity. For general nonlinearities, such uniqueness re-
sults are usually not available. Without this uniqueness result, one obtains a result
corresponding to a weaker notion of stability: stability of the set G. More precisely,
the concept of stability would read as follows: The set of ground states G is said to

170 S
tefan Le Coz
be s
table if for all ε > 0 there exists δ > 0 such that if u
0
∈ H
1
(R
N
) satisfies
ku
0
− ϕk
H
1
(R
N
)
< δ for some ϕ ∈ G then
sup
t∈R
inf
ψ∈G
ku(t) − ψk
H
1
(R
N
)
< ε,
where u is the maximal solution of (1.1) with u(0) = u
0
.
4.2 Grillakis–Shatah–Strauss method
The method of Grillakis–Shatah–Strauss is a powerful tool to derive stability or insta-
bility results. The results in [34, 35] state, roughly speaking, the following: If we con-
sider afamily (ϕ
ω
) of solutions of the stationary equation, the standing wave e
iωt
ϕ
ω
(x)
is stable if
∂
∂ω
kϕ
ω
k
2
L
2
(R
N
)
> 0
(4.7)
and unstable if
∂
∂ω
kϕ
ω
k
2
L
2
(R
N
)
< 0, (
4.8)
provided some spectral assumptions on the linearized operator S
′′
(ϕ
ω
) are satisfied.
Slope conditions of the type (4.7)–(4.8) can easily be checked when the stationary
equation admits some scaling invariance, typically when the nonlinearity is of power
type. For example, in the case of (3.1), it is easy to see that if ϕ
1
is a solution of (3.1)
with ω = 1 then the scaling ϕ
ω
(·) := ω
1
p−1
ϕ
1
(ω
1
2
·) p
rovides a family of solutions of
(3.1) for ω ∈ (0, +∞) such that
∂
∂ω
kϕ
ω
k
2
L
2
(R
N
)
> 0
if p < 1 +
4
N
,
∂
∂ω
kϕ
ω
k
2
L
2
(R
N
)
< 0
if p > 1 +
4
N
.
I
n such situations, the main difficulty is to handle the spectral conditions (see, e.g.,
[25, 26, 49]). If (3.1) has no scaling invariance, it becomes very difficult to obtain the
slope conditions (4.7)–(4.8) (see nevertheless [27, 28, 56]). An alternative is to use
a stability criterion derived from the work [34]. This stability criterion fits better the
case of general nonlinearities, as, e.g., in [19, 23, 24, 40, 44, 46]. See also [72] for
a review of the different ways to obtain stability for general nonlinearities thanks to
Grillakis–Shatah–Strauss’ results.
Although theses notes are restrictedto nonlinear Schrödinger equations with power-
type nonlinearities, our goal is to provide the reader with methods applicable in rather
general situations and this is why we choose to present the proof of Theorem 4.3 using
the following stability criterion.
Proposition 4.10 (Stability criterion). Let ϕ be a solution of (3.1). Suppose that there
exists δ > 0 such that we have
hS
′′
(ϕ)v, vi > δkvk
2
H
1
(R
N
)
(4.9)
Standing waves in nonlinear Schrödinger equations 1
71
for all v ∈ H
1
(R
N
) s
atisfying the orthogonality conditions
(
v, ϕ
)
2
=
(
v, iϕ
)
2
=
v,
∂ϕ
∂x
j
2
= 0 fo
r all j = 1, . . . , N. (4.10)
Then the standing wave e
iωt
ϕ(x) is orbitally stable in H
1
(R
N
).
Let us heuristically explain why the assumptions of Proposition 4.10 lead to sta-
bility. The idea comes from the theory of Lyapunov stability for an equilibrium in
dynamical systems. A good candidate for a Lyapunov functional would be the func-
tional S. Indeed, let us suppose for a moment that the coercivity condition (4.9) holds
for any v ∈ H
1
(R
N
) (this is not the case, as we will see in the sequel). Let u be a
solution of (1.1) with initial datum u
0
close to ϕ in H
1
(R
N
). A Taylor expansion gives
S(u(t)) − S(ϕ) = hS
′
(ϕ), u(t) − ϕi +
1
2
hS
′
′
(ϕ)(u(t) −ϕ), u(t) − ϕi
+o(ku(t) − ϕk
2
H
1
(R
N
)
).
Since ϕ is a solution of (3.1), S
′
(ϕ) = 0. Combined with (4.9), this would give, for
some constant C > 0 independent of t,
S(u(t)) − S(ϕ) > Cku(t) − ϕk
2
H
1
(R
N
)
. (4.11)
Since S is a conserved quantity this would give an upper bound on ku(t) − ϕk
H
1
(R
N
)
,
hence stability. Of course, as we already know (see Remark 4.2), this cannot be true
since stability is possible only up to translations and phase shifts. In fact, translation
and phase shift invariance generates, as we will see in the sequel, a kernel for S
′′
(ϕ) of
the form
ker{S
′′
(ϕ)} = span
iϕ,
∂ϕ
∂x
j
;j = 1,
. . . , N
.
To avoid this kernel, we require the coercivity condition (4.9) only for v ∈ H
1
(R
N
)
satisfying
(
v, iϕ
)
2
=
v,
∂ϕ
∂x
j
2
= 0
for all j = 1, . . . , N,
which allows phase shifts and translations in the right-hand side of (4.11). The other
orthogonality condition
(
v, ϕ
)
2
= 0 is related to the conservation of mass. Indeed,
since the mass is conserved, the evolution takes place, in some sense, in the tangent
space of the sphere of L
2
(R
N
) at ϕ and therefore it is enough to ask for S to satisfy the
coercivity condition (4.9) on this tangent space to get stability. The rigorous proof of
Proposition 4.10 is involved and we have postponed it to the appendix.
In view of Proposition 4.10, it is clear that Theorem 4.3 follows immediately from
the following proposition.
Proposition 4.11. Let 1 < p < 1 +
4
N
and ϕ be a ground state of (3.1). Then there
exists δ > 0 such that for all w ∈ H
1
(R
N
) satisfying
(
w, ϕ
)
2
=
(
w, iϕ
)
2
=
w,
∂ϕ
∂x
j
2
= 0 for all j = 1, . . . , N, (4.12)

172 S
tefan Le Coz
we have
hS
′
′
(ϕ)w, wi > δkwk
2
H
1
(R
N
)
.
Before giving the proof of Proposition 4.11, some preparation is necessary. First,
from Theorem 3.15, we can assume without loss of generality that the ground state ϕ is
real, positive, and radial. Note that uniqueness is not involved here. It is convenient to
split w in the real and imaginary part. We set w = u+iv for real-valued u, v ∈ H
1
(R
N
).
Then the operator S
′′
(ϕ) can be separated into a real and an imaginary part L
1
and L
2
such that
hS
′′
(ϕ)w, wi = hL
1
u, ui + hL
2
v, vi.
Here, L
1
and L
2
are two bounded operators defined on H
1
(R
N
) restricted to real-
valued functions, with values in H
−1
(R
N
), and given by
L
1
u = −∆u + ωu − pϕ
p−1
u,
L
2
v = −∆v + ωv − ϕ
p−1
v.
Until the end of this subsection, the functions considered will be real-valued. In partic-
ular, H
1
(R
N
) and L
2
(R
N
) will be restricted to real-valued functions.
Proposition 4.11 follows immediately from the two following lemmas.
Lemma 4.12. There exists δ
1
> 0 such that for all u ∈ H
1
(R
N
) satisfying
(
u, ϕ
)
2
=
u,
∂ϕ
∂x
j
2
= 0 fo
r all j = 1, . . . , N,
we have
hL
1
u, ui > δ
1
kuk
2
H
1
(R
N
)
.
Lemma 4.13. There exists δ
2
> 0 such that for all v ∈ H
1
(R
N
) satisfying
(
v, ϕ
)
2
= 0,
we have
hL
2
v, vi > δ
2
kvk
2
H
1
(R
N
)
.
It is not hard to see that the operators L
1
and L
2
admit restrictions
˜
L
1
and
˜
L
2
with
domain H
2
(R
N
) that are unbounded self-adjoint operators in L
2
(R
N
) (the so-called
Friedrichs extensions, see, e.g., [43]).
The proofs of Lemmas 4.12 and 4.13 rely on the analysis of the spectra of
˜
L
1
and
˜
L
2
. The following lemma gives the general structure of these spectra.
Lemma 4.14. The spectra of
˜
L
1
and
˜
L
2
consist of essential spectrum in [ω, +∞) and
of a finite number of eigenvalues of finite multiplicity in (−∞, ω
′
] for all ω
′
< ω.

Standing waves in nonlinear Schrödinger equations 1
73
Proof. W
e first remark that since
˜
L
1
and
˜
L
2
are self-adjoint operators, their spectra lie
on the real line.
The spectra of
˜
L
1
and
˜
L
2
are bounded from below. Indeed, for all u ∈ H
1
(R
N
), we
have
hL
2
u, ui = k∇uk
2
L
2
(R
N
)
+ ωkuk
2
L
2
(R
N
)
−
Z
R
N
ϕ
p−1
u
2
dx
> k∇uk
2
L
2
(R
N
)
+ ωkuk
2
L
2
(R
N
)
− p
Z
R
N
ϕ
p−1
u
2
dx = hL
1
u, ui.
Since ϕ ∈ L
∞
(R
N
), there exists C > 0, independent of u, such that
p
Z
R
N
ϕ
p−1
u
2
dx 6 Ckuk
2
L
2
(R
N
)
and therefore
hL
2
u, ui > hL
1
u, ui > (ω − C)kuk
2
L
2
(R
N
)
.
Now, since ϕ is exponentially decaying,
˜
L
1
and
˜
L
2
are compactly perturbed ver-
sions of
−∆ + ω : H
2
(R
N
) ⊂ L
2
(R
N
) → L
2
(R
N
).
It is well known that the essential spectrum of −∆ + ω is σ
ess
(−∆ + ω) = [ω, +∞),
thus, by Weyl’s Theorem (see, e.g., [43]),
σ
ess
(
˜
L
1
) = σ
ess
(
˜
L
2
) = [ω, +∞).
Since, for j = 1, 2, σ(
˜
L
j
) \σ
ess
(
˜
L
j
) consists of isolated eigenvalues of finite multiplic-
ity and σ(
˜
L
j
) is bounded from below, this completes the proof of the lemma.
From now on, we consider L
1
a
nd L
2
separately. We begin with L
2
.
Lemma 4.15. There exists
˜
δ
2
> 0 such that for all v ∈ H
1
(R
N
) with
(
v, ϕ
)
2
= 0, we
have
hL
2
v, vi >
˜
δ
2
kvk
2
L
2
(R
N
)
.
Proof. We remark that L
2
ϕ = S
′
(ϕ) = 0 since ϕ is a solution of (3.1). This means
that 0 is an eigenvalue of L
2
with ϕ being an eigenfunction. But ϕ > 0, and it is
well known (see, e.g., [11]) that this implies that 0 is the first simple eigenvalue of
˜
L
2
.
Let v ∈ H
1
(R
N
) be such that
(
v, ϕ
)
2
= 0. Then, by the min-max characterization
of eigenvalues (see, e.g., [11]), there exists
˜
δ
2
> 0 independent of v (in fact,
˜
δ
2
is the
second eigenvalue of
˜
L
2
) such that
hL
2
v, vi >
˜
δ
2
kvk
2
L
2
(R
N
)
.

174 S
tefan Le Coz
Proof of Lemma 4.13. T
he proof is carried out by contradiction. Assume the existence
of a sequence (v
n
) ⊂ H
1
(R
N
) such that
k∇v
n
k
2
L
2
(R
N
)
+ ωkv
n
k
2
L
2
(R
N
)
= 1,
(
v
n
, ϕ
)
2
= 0 and hL
2
v
n
, v
n
i → 0 as n → +∞.
Since kv
n
k
2
H
1
(R
N
)
≤ max{ω, ω
−1
}(k∇v
n
k
2
L
2
(R
N
)
+ ωkv
n
k
2
L
2
(R
N
)
), (v
n
) is bounded in
H
1
(R
N
) and there exists v ∈ H
1
(R
N
) such that, possibly for a subsequence only,
v
n
⇀ v weakly in H
1
(R
N
).
In particular, we have
(
v, ϕ
)
2
= 0 and by Lemma 4.15
hL
2
v, vi > 0. (4.13)
By the embedding of H
1
(R
N
) into L
2q
(R
N
) for q ∈ (1, (N − 2)/N), we have v
n
⇀ v
in L
2q
(R
N
). In view of the compact embedding of H
1
(R
N
) into L
2q
loc
(R
N
), we also get
v
2
n
⇀ v
2
in L
q
(R
N
). Since ϕ is exponentially decaying, we have ϕ
p−1
∈ L
q
′
(R
N
),
where q
′
is the conjugate exponent of q,
1
q
+
1
q
′
= 1
. Therefore,
Z
R
N
ϕ
p−1
v
2
n
dx →
Z
R
N
ϕ
p−1
v
2
dx as n → +∞. (4.14)
From (4.14) and by the weak lower semi-continuity of the H
1
(R
N
)-norm, we infer that
hL
2
v, vi 6 liminf
n→+∞
hL
2
v
n
, v
n
i = 0. (4.15)
Combined with (4.13), (4.15) implies hL
2
v, vi = 0. Since
(
ϕ, v
)
2
= 0, we obtain by
Lemma 4.15
v ≡ 0. (4.16)
On the other hand,
0 = liminf
n→+∞
hL
2
v
n
, v
n
i = 1 −
Z
R
N
ϕ
p−1
v
2
dx.
Hence
R
R
N
ϕ
p−1
v
2
dx = 1, which is in contradiction with (4.16).
We now turn our attention to L
1
.
The proof of Lemma 4.12 is more delicate, essen-
tially since the spectrum of
˜
L
1
contains nonpositive eigenvalues. Furthermore, ϕ is no
longer an eigenfunction. We first deal with the negative eigenvalues of
˜
L
1
.
Lemma 4.16. The operator
˜
L
1
has only one negative eigenvalue −λ
1
with a corre-
sponding eigenfunction e
1
∈ H
2
(R
N
) such that ke
1
k
L
2
(R
N
)
= 1.
Proof. Let
˜
S : H
1
(R
N
) → R be the restriction of S to real-valued functions. It is not
hard to see that ϕ is also a mountain pass critical point of
˜
S. Then it is well known
(see, for example, [3]) that the Morse index of
˜
S at ϕ is at most 1 (recall that the Morse
