Emmrich E., Wittbold P. (editors) Analytical and Numerical Aspects of Partial Differential Equations: Notes of a Lecture Series
Подождите немного. Документ загружается.

Coupling of a scalar conservation law with a parabolic problem 145
Lemma 4.11. Let G : R → R be Hölder continuous with exponent α ∈ (0, 1). Then
G(v) ∈ W
αs,
p
α
(Ω) for any v ∈ W
s,p
(Ω), 0 < s < 1, 1 < p < ∞, and the mapping
G : W
s,p
(Ω) → W
αs,
p
α
(Ω) is bounded.
Proof of Proposition 4.10. Note first that (4.13) implies that there exists a subsequence,
still denoted by (u
µ
)
µ>0
, such that u
µ
∗
* u in L
∞
(Q). The two convergence results
about λ
µ
∇φ(u
µ
) are an immediate consequence of (4.15). So we just have to prove the
strong convergence of (u
µ
)
µ>0
in L
q
(Q
p
). To do so, we refer to the arguments used in
[9, Chapt. 2].
From (4.16), (∂
t
u
µ
)
µ>0
is bounded in L
2
(0, T ; H
−1
(Ω
p
)). Moreover, due to (4.13)
and (4.15), the sequence (φ(u
µ
))
µ>0
is bounded in L
2
(0, T ; V ). For any s ∈ (0, 1), we
also have
L
2
(0, T ; V ) ,→ L
2
(0, T ; H
1
(Ω
p
)) ,→ L
2
(0, T ; W
s,2
(Ω
p
)).
Since u
µ
= φ
−1
(φ(u
µ
)), by (4.17) and Lemma 4.11, we assert that u
µ
is bounded
in L
2/τ
(0, T ; W
τs,2/τ
(Ω
p
)). The compactness of the embedding of W
τs,2/τ
(Ω
p
) in
L
2/τ
(Ω
p
) and the Lions–Aubin compactness theorem (see [14, p. 57]) ensure that
W := {v ∈ L
2/τ
(0, T ; W
τs,2/τ
(Ω
p
)); ∂
t
v ∈ L
2
(0, T ; H
−1
(Ω
p
))}
is compactly embedded in L
2/τ
(0, T ; L
2/τ
(Ω
p
)). Hence, the conclusion follows.
We are now able to state the main theorem of this section.
Theorem 4.12. Problem (1.1) has a weak entropy solution that is the limit of the se-
quence (u
µ
)
µ>0
of solutions to (4.12) in L
q
(Q), 1 ≤ q < ∞, as µ → 0
+
.
Proof. We consider the function u given in Proposition 4.10. Because of (4.13), we
can apply Theorem 1.5 to assert that there exists a function π ∈ L
∞
((0, 1) × Q
h
) such
that for any continuous and bounded function ψ on Q
h
× [m, M] and ξ ∈ L
1
(Q
h
)
lim
µ→0
+
Z
Q
h
ψ(t, x, u
µ
(t, x))ξdxdt =
Z
1
0
Z
Q
h
ψ(t, x, π(α, t, x))ξdxdtdα. (4.18)
Our aim is first to establish that, as in Section 3, the process π is reduced to u
|Q
h
and, second, to prove that u is a weak entropy solution to (1.1).
In order to do so, we come back to (4.14) and, for any real k, we choose the test
function v
µ
η
= sgn
η
(φ(u
µ
) − φ(k))ϕ
1
ϕ
2
, where ϕ
1
∈ C
∞
(−T, T ), ϕ
2
∈ C
∞
c
(Ω) with
ϕ
1
, ϕ
2
≥ 0. Thereby, we obtain
h∂
t
u
µ
, v
µ
η
i +
Z
Ω
(λ
µ
(x)∇φ(u
µ
) − b(x)f(u
µ
)) · ∇v
µ
η
dx = 0.
We integrate with respect to the time variable and perform the following transforma-
tions in a same way as in Section 3. Thanks to a generalization of Lemma 1.1 (see

146 Julien Jimenez
[18]), the evolutionary term may be written as
Z
T
0
h∂
t
u
µ
, sgn
η
(φ(u
µ
) − φ(k))ϕ
2
iϕ
1
dt
= −
Z
Q
I
η
(u
µ
)ϕ
2
∂
t
ϕ
1
dxdt −
Z
Ω
I
η
(u
0
)ϕ
2
ϕ
1
(0)dx
with I
η
(u
µ
) =
Z
u
µ
k
sgn
η
(φ(τ) − φ(k))dτ . For the diffusion term, we obtain
Z
Q
λ
µ
(x)∇φ(u
µ
) · ∇v
µ
η
dxdt ≥
Z
Q
λ
µ
sgn
η
(φ(u
µ
) − φ(k))∇φ(u
µ
) · ∇ϕ
2
ϕ
1
dxdt.
Moreover, we have
Z
Q
b(x)f(u
µ
) · ∇v
µ
η
dxdt = −
Z
Q
b(x)F
η
(u
µ
)∇ϕ
2
ϕ
1
dxdt
with F
η
(u
µ
) =
Z
u
µ
k
f
0
(τ)sgn
η
(φ(τ) − φ(k))dτ .
We take the limit with respect to µ separately on the hyperbolic and parabolic area.
On Q
h
, we take advantage of (4.18), while on Q
p
, we use Proposition 4.10. In this
way, we obtain
Z
Q
p
I
η
(u)ϕ
2
∂
t
ϕ
1
+ b(x)F
η
(u) · ∇ϕ
2
ϕ
1
dxdt
+
Z
1
0
Z
Q
h
I
η
(π)ϕ
2
∂
t
ϕ
1
+ b(x)F
η
(π) · ∇ϕ
2
ϕ
1
dxdtdα
−
Z
Q
p
sgn
η
(φ(u) − φ(k))∇(φ(u) − φ(k)) · ∇ϕ
2
ϕ
1
dxdt
+
Z
Ω
I
η
(u
0
)ϕ
2
ϕ
1
(0)dx ≥ 0.
Then we take the limit with respect to η. We remark that
lim
η→0
+
F
η
(u) = sgn(φ(u) − φ(k))(f (u) − f(k)) = F (u, k) a.e. on Q
h
and Q
p
.
Therefore, we get in the limit
Z
Q
p
|u − k|ϕ
2
∂
t
ϕ
1
+ b(x)F(u, k) · ∇ϕ
2
ϕ
1
dxdt
+
Z
1
0
Z
Q
h
|π − k|ϕ
2
∂
t
ϕ
1
+ b(x)F(π, k) · ∇ϕ
2
ϕ
1
dxdtdα
+
Z
Ω
|u
0
− k|ϕ
2
ϕ
1
(0)dx −
Z
Q
p
∇|φ(u) − φ(k)| · ∇ϕ
2
ϕ
1
dxdt ≥ 0. (4.19)

Coupling of a scalar conservation law with a parabolic problem 147
We justify now that π satisfies the initial condition (4.3) and the boundary condition
(4.4). When we consider test functions ϕ
2
that belong to C
∞
c
(Ω
h
), we deduce that
−
Z
1
0
Z
Q
h
|π − k|ϕ
2
∂
t
ϕ
1
+ b(x)F(π) · ∇ϕ
2
ϕ
1
dxdtdα ≤
Z
Ω
h
|u
0
− k|ϕ
2
ϕ
1
(0)dx.
Therefore, we can apply Lemma 3.13 (with Q = Q
h
) to state that
esslim
t→0
+
Z
1
0
Z
Ω
h
|π(α, t, x) − u
0
(x)|dxdα = 0. (4.20)
Hence, π fulfills the initial condition (4.3) on Ω
h
.
Next we choose in (4.14) the test function v
δ
= ∂
1
H
δ
(u
µ
, k)ϕ
1
ϕ
2
(see Example 3.4
for the definition of H
δ
), where ϕ
1
∈ C
∞
c
(0, T ), ϕ
2
∈ C
∞
(Ω
h
) with ϕ
2
= 0 on Γ
hp
,
ϕ
1
, ϕ
2
≥ 0. We take the limit with respect to η and apply Lemma 3.14 to assert that,
for any nonnegative β ∈ L
1
(Σ
h
\ Σ
hp
)
ess lim
s→0
−
Z
1
0
Z
Σ
h
\Σ
hp
J
δ
(π(α, σ + sν
h
), k)βb(σ) · ν
h
dσdα ≥ 0,
where J
δ
is defined in Example 3.4. As δ → 0
+
, we obtain that π satisfies (4.4).
Therefore, π fulfills (4.2) for all ϕ ∈ C
∞
c
(Q
h
) as well as (4.3) and (4.4), where integrals
over Q
h
, Ω
h
and Σ
h
\ Σ
hp
are replaced by integrals over (0, 1) × Q
h
, (0, 1) × Ω
h
and
(0, 1) × Σ
h
\ Σ
hp
, respectively, with respect to the corresponding measure. Then, by
reasoning as in Theorem 4.5, if π
1
(α, ·) and π
2
(β, ·) are two process solutions for initial
data u
0,1
and u
0,2
, we obtain for almost all t ∈ (0, T )
Z
1
0
Z
1
0
Z
Ω
h
|π
1
(α, t, x) − π
2
(β, t, x)|dxdαdβ ≤
Z
Ω
h
|u
0,1
− u
0,2
|dx.
Therefore, if u
0,1
= u
0,2
on Ω
h
, there exists a bounded function u
h
on Q
h
such that
a.e. on Q
h
,
u
h
(·) = π
1
(α, ·) = π
2
(β, ·) for almost all α and β in (0, 1).
Besides, u
h
= u
|Q
h
a.e. on Q
h
. Thus, from (4.19), it follows that u fulfills (4.2) for all
ϕ ∈ C
∞
c
(0, T ) ⊗ C
∞
c
(Ω) and, by density, for all ϕ ∈ C
∞
c
(Q) as well as (4.4).
To complete the proof it remains to show that (4.3) holds for u. Due to (4.20), we
just have to focus on Ω
p
. We consider (4.19) for ϕ
2
∈ C
∞
c
(Ω
p
). This yields
−
Z
T
0
Z
Ω
p
|u − k|ϕ
2
dx + g(t)
!
ϕ
0
1
(t)dt ≤
Z
Ω
p
|u
0
− k|ϕ
2
ϕ(0)dx
with
g(t) =
Z
Ω
p
Z
t
0
(
|φ(u(τ, x)) − φ(k)|∆ϕ
2
− sgn(u(τ, x) − k)(f (u(τ, x) − f(k))b(x) · ∇ϕ
2
)
dτdx.
148 Julien Jimenez
Therefore, the time-depending function
t 7→
Z
Ω
p
|u − k|ϕ
2
dx + g(t)
can be identified a.e. with a nonincreasing and bounded function. Then it has an essen-
tial limit as t → 0
+
. Since g(t) → 0 as t → 0
+
, it follows
esslim
t→0
+
Z
Ω
p
|u − k|ϕ
2
dx ≤
Z
Ω
p
|u
0
− k|ϕ
2
dx,
for all nonnegative ϕ
2
∈ C
∞
c
(Ω
p
), which implies (see [17]), for any k ∈ L
∞
(Ω
p
),
esslim
t→0
+
Z
Ω
p
|u − k(x)|dx ≤
Z
Ω
p
|u
0
− k(x)|dx.
We choose k = u
0
to ensure that u satisfies (4.3). This concludes the proof.
5 Concluding remarks
We end these lecture notes by some remarks. We have studied a simplified coupling
problem. One could, for example, also assume, as in [1, 12], that the nonlinearities are
different on Q
h
and Q
p
. Indeed, we could consider the following problem: Find a mea-
surable and essentially bounded function u on Q such that in the sense of distributions
∂
t
u + ∇ · (b
h
(x)f
h
(u)) = 0 in Q
h
,
∂
t
u + ∇ · (b
p
(x)f
p
(u)) = ∆φ(u) in Q
p
,
u = 0 on (0, T ) × ∂Ω,
u(0, ·) = u
0
on Ω.
(5.1)
In this case, the notion of weak entropy solution in Definition 4.2 is not suitable
anymore. We have to add in the entropy formulation (4.2) an interface integral that
takes into account the discontinuity of the flux function along Σ
hp
. Indeed, setting
b(x)f(u) = b
h
(x)f
h
(u)χ
Ω
h
+ b
p
(x)f
p
(u)χ
Ω
p
, we propose the following definition of
a weak entropy solution.
Definition 5.1. A function u is said to be a weak entropy solution to (5.1) if
(i) u ∈ L
∞
(Q), φ(u) ∈ L
2
(0, T ; V ),
(ii) for all nonnegative ϕ ∈ C
∞
c
(Q)and all k ∈ R
Z
Q
(|u − k|∂
t
ϕ + (b(x)F (u, k) − ∇|φ(u) − φ(k)|) · ∇ϕ)dxdt
+
Z
Σ
hp
(b
h
(σ)f
h
(k) − b
p
(σ)f
p
(k)) · ν
h
sgn(φ(u) − φ(k))dσ ≥ 0.
Coupling of a scalar conservation law with a parabolic problem 149
(iii) u satisfies the initial condition (4.3) and the boundary condition (4.4).
We refer to [11, Chap. 4] or [12] for the study of (5.1). When we use the vanishing
viscosity method, the major difficulty relies on the study of the viscous problem related
to (5.1). Roughly speaking, we are not able to prove the maximum principle without
additional assumption on the flux. We also underline that the existence and uniqueness
results of [12] are obtained in the framework of outwards characteristics (see Remark
4.1). The case of inwards characteristics, i.e., the case where the characteristics are
entering the hyperbolic zone, is treated in [2] for (1.1). We emphasize the fact that the
general case (i.e., no assumption on the characteristics) is still an open problem.
Acknowledgments. I warmly thank Petra Wittbold and Etienne Emmrich for their kind
invitation at the Technische Universität Berlin. Moreover, their remarks, suggestions
and comments greatly improved these lecture notes. I also would like to thank the
Stiftung Luftbrückendank for supporting my stay in Berlin.
References
[1] G. Aguilar, L. Lévi and M. Madaune-Tort, Coupling of multidimensional parabolic and hyper-
bolic equations, J. Hyperbolic Differ. Equ. 3 (2006), pp. 53–80.
[2] , Nonlinear multidimensional parabolic-hyperbolic equations, 2006 International con-
ference in honor of J. Fleckinger, Electron. J. Diff. Eqns. Conf. 16 (2007), pp. 15–28.
[3] G. Aguilar, F. Lisbona and M. Madaune-Tort, Analysis of a nonlinear parabolic-hyperbolic
problem, Adv. Math. Sci. Appl. 7 (1997), pp. 165–181.
[4] C. Bardos, A. Y. LeRoux and J. C. Nédélec, First order quasilinear equations with boundary
conditions, Commun. Partial Differ. Equations 4 (1979), pp. 1017–1034.
[5] R. Dautray and J. L. Lions, Analyse mathématique et calcul numérique pour les sciences et
techniques, vol. 8, Masson, Paris, 1980.
[6] , Mathematical analysis and numerical methods for science and technology, vol. 5,
Springer, Berlin, 1992.
[7] L. C. Evans and R. F. Gariepy, Measure theory and fine properties of functions, CRC Press,
London, 1992.
[8] R. Eymard, T. Gallouët and R. Herbin, Existence and uniqueness of the nonlinear hyperbolic
equation, Chin. Ann. Math. Ser. B 16 (1995), pp. 1–14.
[9] G. Gagneux and M. Madaune-Tort, Analyse mathématiques de modèles non linéaires de
l’ingénierie pétrolière, Springer, Berlin, 1996.
[10] E. Godlewski and P. A. Raviart, Hyperbolic systems of conservation laws, Mathématiques et
Applications, S.M.A.I., Ellipses, Paris, 1991.
[11] J. Jimenez, Modèles non linéaires de transport dans un milieu poreux hétérogène, Ph.D. thesis,
Univ. Pau, 2007.
[12] J. Jimenez and L. Lévi, Entropy formulations for a class of scalar conservation laws with space-
discontinuous flux functions in a bounded domain, J. Engrg. Math. 60 (2008), pp. 319–335.
[13] S. N. Kružkov, First order quasilinear equations with several independent variables, Mat. Sb.
81:123 (1970), pp. 228–255.

150 Julien Jimenez
[14] J. L. Lions, Quelques méthodes de résolution des problèmes aux limites non linéaires, Dunod,
Gauthier-Villars, Paris, 1969.
[15] J. Málek, J. Ne
ˇ
cas, M. Rokyta and M. R˚uži
ˇ
cka, Weak and measure-valued solutions to evolu-
tionary PDEs, Chapman & Hall, London, 1996.
[16] M. Marcus and V. J. Mizel, Every superposition mapping one Sobolev space into another is
continuous, J. Funct. Anal. 33 (1979), pp. 217–229.
[17] F. Otto, Initial-boundary value problem for a scalar conservation law, C. R. Acad. Sci. Paris,
Sér. I 322 (1996), pp. 729–734.
[18] , L
1
-contraction and uniqueness for quasilinear elliptic-parabolic equations, J. Dif-
fer. Equations 131 (1996), pp. 20–38.
[19] J. Wloka, Partial differential equations, Cambridge University Press, Cambridge, 1987.
Author information
Julien Jimenez, Laboratory of applied mathematics, University of Pau, BP 1155, 64013 Pau Cedex,
France.
E-mail:

Analytical and Numerical Aspects of Partial Differential Equations ©
de Gruyter 2009
Standing waves in nonlinear Schrödinger equations
S
tefan Le Coz
Abstract. In the theory of nonlinear Schrödinger equations, it is expected that the solutions will ei-
ther spread out because of the dispersive effect of the linear part of the equation or concentrate at one
or several points because of nonlinear effects. In some remarkable cases, these effects counterbal-
ance, and special solutions that neither disperse nor focus appear, the so-called standing waves. For
the physical applications as well as for the mathematical properties of the equation, a fundamental
issue is the stability of waves with respect to perturbations. Our purpose in these notes is to present
various methods developed to study the existence and stability of standing waves. We prove the
existence of standing waves by using a variational approach. When stability holds, it is obtained by
proving a coercivity property for a linearized operator. Another approach based on variational and
compactness arguments is also presented. When instability holds, we show by a method combining
a virial identity and variational arguments that the standing waves are unstable by blow-up.
Keywords. Nonlinear Schrödinger equation, standing waves, orbital stability, instability, blow-up,
variational methods.
AMS classification. 35Q55, 35Q51, 35B35, 35A15.
1 Introduction
In these lecture notes, we consider the nonlinear Schrödinger equation
i∂
t
u + ∆u + |u|
p−1
u = 0. (1.1)
Equation (1.1) arises in various physical and biological contexts, for example in non-
linear optics, for Bose–Einstein condensates, in the modelling of the DNA structure,
etc. We refer the reader to [14, 73] for more details on the physical background and
references.
Here, the unknown u is a complex valued function of t ∈ R and x ∈ R
N
for N > 1,
u : R ×R
N
→ C.
In most of the applications, t stands for the time and x for the space variable, but
sometimes it can be the converse, for example in nonlinear optics. The number i is the
imaginary unit (i
2
= −1), ∂
t
is the first derivative with respect to the time t, ∆ denotes
the Laplacian with respect to the space variable x (∆ =
P
N
j=1
∂
2
∂x
2
j
). Finally, p ∈ R is
such that p > 1, which means that the equation is superlinear.
To simplify the exposition, we have restricted ourselves to the study of nonlinear
Schrödinger equations with a power-type nonlinearity, but one can also consider more
general versions of these equations, see [14, 73] and the references cited therein.
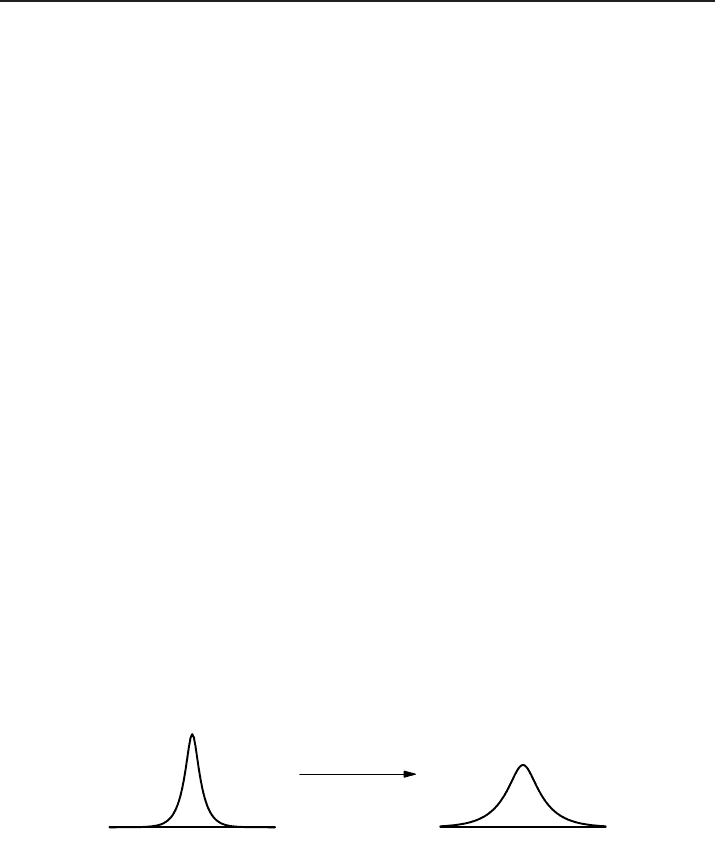
152 S
tefan Le Coz
The purpose of these notes is to study the properties of particular solutions of (1.1)
o
f the form e
iωt
ϕ(x) with ω ∈ R and ϕ satisfying
−∆ϕ + ωϕ −|ϕ|
p−1
ϕ = 0. (1.2)
Such solutions are called standing waves. They are part of a more general class of so-
lutions arising for various nonlinear equations like Korteweg–de Vries, Klein–Gordon
or Kadomtsev–Petviashvili equations. These equations enjoy special solutions whose
profile remains unchanged under the evolution in time. These special solutions are
called solitary waves or solitons (see [14, 18, 20, 73] for an overview of physical and
mathematical questions around solitary waves).
This kind of phenomena was discovered in 1834 by John Scott Russel. The Scottish
engineer was supervising work in a canal near Edinburgh when he observed that the
brutal stop of a boat in the canal was creating a wave that does not seem to vanish.
Indeed, he was able to follow this wave horseback on a distance of several miles. His
life long, he studied this surprising phenomenon but without being able to give it a
theoretical justification. In fact, most of the scientists of that time did believe that such
a wave, which does not disperse, could not exist. The first theoretical justification of the
existence of solitary waves was given by Korteweg and de Vries in 1895. They derived
an equation for the motion of water admitting solitary wave solutions. But one had to
wait until the 1950’s to see the beginning of an intensive research from mathematicians
and physicists about solitary waves.
Heuristically, such solutions appear because of the balance of two contradictory
effects: the dispersive effect of the linear part, which tends to flatten the solution as
time goes on (see Figure 1), and the focusing effect of the nonlinearity, which tends to
concentrate the solution, provided the initial datum is large enough (see Figure 2). For
Figure 1. D
ispersive effect.
some special initial data, each effect compensates the other and the general profile of
the initial data remains unchanged (see Figure 3).
In the study of standing waves, two types of questions arise naturally.
(i) Do standing waves exist, i.e., does (1.2) admit nontrivial solutions? If yes, what
kind of properties for the solutions of (1.2) can be shown: Are they regular, what
is their decay at infinity, can we find variational characterizations for at least some
of these solutions?
Standing waves in nonlinear Schrödinger equations 1
53
Figure 2. F
ocusing effect.
Figure 3. B
alance between dispersion and focusing.
(ii) If standing waves exist, are they stable (in a sense to be made precise) as solutions
of (1.1)? If they are unstable, what is the nature of instability?
The first type of questions is related to the study of existence of solutions for semili-
near elliptic problems. The methods used in this context are often of variational nature
and solutions are obtained by minimization under constraint or with min-max argu-
ments. The second type of questions concerns the dynamics of the evolution equation.
Nevertheless, both problems are intimately related. Indeed, informations of variational
nature on the solutions of the stationary equation are essential to derive stability or
instability results.
The rest of these notes is divided into four sections and an appendix. We first give
basic results on the Cauchy problem for (1.1) in Section 2. In Section 3, we study the
existence of standing waves. Section 4 is devoted to stability whereas Section 5 deals
with instability. The proof of a stability criterion is given in the appendix.
Notation. The space of complex measurable functions whose r-th power is integrable
will be denoted by L
r
(R
N
) and its standard norm by k · k
L
r
(R
N
)
. When r = 2, the
space L
2
(R
N
) will be endowed with the real inner product
(
u, v
)
2
= Re
Z
R
N
u ¯vdx for u, v ∈ L
2
(R
N
).
The space of functions from L
r
(R
N
) whose distributional derivatives of order less than
or equal to m are elements of L
r
(R
N
) will be denoted by W
m,r
(R
N
). If m = 1 and

154 S
tefan Le Coz
r = 2
, we shall denote W
1,2
(R
N
) by H
1
(R
N
), its usual norm by k · k
H
1
(R
N
)
and the
duality product between the dual space H
−1
(R
N
) and H
1
(R
N
) by h·, ·i. If m = r = 2,
we denote W
2,2
(R
N
) by H
2
(R
N
).
For notational convenience, we shall sometimes identify a function and its value at
some point. For example, we shall write e
iωt
ϕ(x) for the function (t, x) 7→ e
iωt
ϕ(x).
Similarly, we shall say that |x|v ∈ L
2
(R
N
) if the function x 7→ |x|v(x) belongs to
L
2
(R
N
). For a solution u of (1.1), we shall denote by u(t) the function x 7→ u(t, x).
Therefore, depending on the context, u may denote either a mapping from R to some
function space or a mapping from R ×R
N
to C.
We make the convention that when we take a subsequence of a sequence (v
n
) we
denote it again by (v
n
).
The letter C will denote various positive constants whose exact values may change
from line to line but are not essential in the course of the analysis.
2 The Cauchy problem
For the physical properties of the model as well as for the mathematical study of the
equation, it is interesting to look for quantities conserved along the time. At least
formally, equation (1.1) admits three conserved quantities. The first one is the mass or
charge: If u satisfies (1.1) with initial datum u(0) = u
0
then
Q(u(t)) :=
1
2
ku(t
)k
2
L
2
(R
N
)
≡ Q(u
0
). (2.1)
The conservation of mass is obtained from multiplying (1.1) with ¯u, integrating over
R
N
and taking the imaginary part. The second conserved quantity is the energy (mul-
tiply (1.1) by ∂
t
¯u, integrate over R
N
and take the real part),
E(u(t)) :=
1
2
k
∇u(t)k
2
L
2
(R
N
)
−
1
p + 1
ku(t
)k
p+1
L
p+1
(R
N
)
≡ E(u
0
). (2.2)
Finally, multiplying (1.1) by ∇¯u, integrating over R
N
and taking the real part, we
obtain the conservation of momentum,
M(u(t)) := Im
Z
R
N
u(t)∇¯u(t)dx ≡ M (u
0
).
Among these three conserved quantities, the mass and the energy are real-valued, but
the momentum may be complex-valued, which makes it less convenient to use.
To benefit from the conserved quantities, it is natural to search solutions of (1.1)
in function spaces where these quantities are well-defined. Consequently, we look
for solutions of (1.1) in H
1
(R
N
) and restrict the range of p to be subcritical for the
Sobolev embedding of H
1
(R
N
) into L
p+1
(R
N
), i.e., 1 < p < 1 +
4
N−2
if N > 3 and
1 < p < +∞ if N = 1, 2. Then we have the following result concerning the well-
posedness of the Cauchy problem for (1.1) (see [14] and the references cited therein).
