Емельянов В.Ю. Методы моделирования стохастических систем управления

Подождите немного. Документ загружается.

формируется случайным образом. Вероятности реализации ее возможных

вариантов могут быть рассчитаны на основе матрицы B.

Рассмотренные формы описания соответствуют наиболее общему слу-

чаю вероятностного автомата. Частные случаи вероятностных автоматов

соответствуют рассмотренным выше видам конечных автоматов.

1. Вероятностный автомат Мили может быть задан таблицей переходов

(табл. 4) и таблицей выходов (табл. 5), элементы которых должны удовлетво-

рять следующим требованиям:











, k=1,2,...,K; K=IJ;

, s=(i,l), i=1,2,...,I; l=1,2,...,L; k=1,2,...,K.

Последнее из указанных соотношений означает статистическую незави-

симость распределений вероятностей нового состояния автомата и выходно-

го сигнала.

Та б л ица 4

Та б л ица 5

Таблица переходов

Таблица выходов

...

Частными случаями всех видов вероятностных автоматов являются Z-

детерминированные и Y-детерминированные автоматы. Рассмотрим их на

примере автомата Мили.

В Z-детерминированном автомате функция переходов  является де-

терминированной, а функция выходов - статистической. Функция переходов

для него может быть задана табл. 1 переходов, матрицей соединений С или

графом (рис.12,б). Законы распределения выходных сигналов задаются мат-

рицей переходных вероятностей B размерностью KL или соответствующей

таблицей.

В Y-детерминированном автомате функция выходов  является детер-

минированной, а функция переходов - статистической. Функция выходов

здесь может быть задана вектором выходов Y, а законы распределения новых

состояний - матрицей переходных вероятностей B размерностью KI.

2. Вероятностный автомат Мура задается таблицей переходов (табл. 4) и

таблицей выходов (табл. 6), по-

строенной в предположении, что

распределение вероятностей

выходных сигналов зависит толь-

ко от состояния автомата. Эле-

менты таблиц должны отвечать

следующим требованиям:







, k=1,2,...,K; K=IJ;







, i=1,2,...,I;

, s=(i,l);

i=1,2,...,I; l=1,2,...,L; k=1,2,...,K.

3. Автономный вероятностный автомат удобнее всего рассматривать и

задавать как частный случай вероятностного автомата Мура при условии

эквивалентности множеств G и Z. Наибольшее практическое использование

получил Y-детерминированный автономный автомат, задаваемый матрицей

переходных вероятностей:

IIIiI

iIiii

ppp











1111



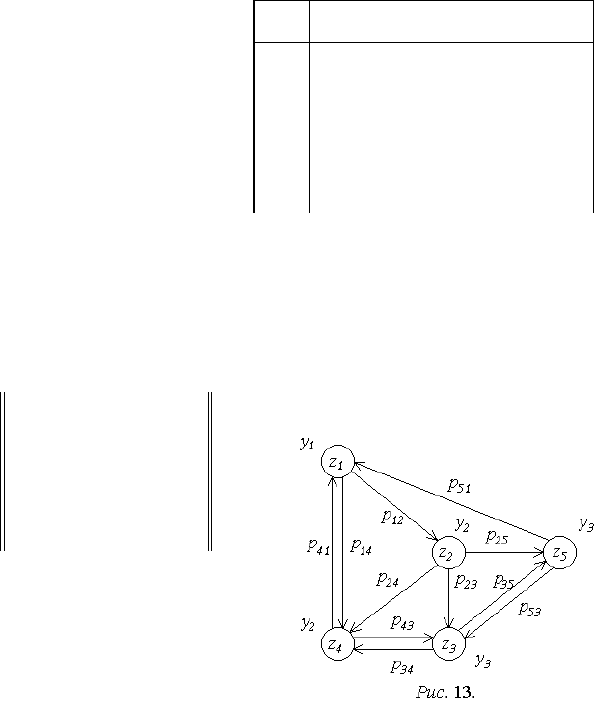
вектором Y или графом (например,

рис. 13). Вершины графа соответст-

вуют состояниям автомата, дуги -

возможным переходам. Около дуг

указываются соответствующие

ходные вероятности, около вершин -

Та б л ица 6

Таблица выходов

...

формируемые выходные сигналы. Модель в форме такого автомата называ-

ется также дискретной марковской цепью.

Вероятностные автоматы без выхода или без памяти можно

расcматривать как частные случаи автомата Мили и использовать соответст-

вующие способы описания.

Выше был приведен пример формализации работы устройства управ-

ления системы обеспечения безопасности движущегося объекта в виде де-

терминированной F-схемы. Если дополнить такую модель частными показа-

телями эффективности отдельных устройств информационной подсистемы,

можно построить модель, позволяющую оценивать эффективность всей

информационной подсистемы в рамках комбинированной схемы (рис. 8).

Эта модель будет иметь вид вероятностного автомата.

Предположим, что алгоритм УУ допускает формализацию в виде авто-

мата без памяти F=X,Y,, и функция выходов  представлена в виде

вектора размерностью J:





, (2.11)

где y

- элементы выходного алфавита Y=(y

,…,y

), то есть меры

обеспечения безопасности, предусмотренные алгоритмом УУ для различных

Условием принятия в УУ решений, соответствующих (2.11), является об-

наружение устройствами информационной подсистемы угрожающих безо-

пасности объекта факторов внешней среды и правильное определение их

характеристик, то есть точное определение x

, что в реальных условиях может

не обеспечиваться.

Предположим, что в текущей ситуации применения системы прису тст-

вуют два угрожающих фактора внешней среды Ц

и Ц

, причем Ц

является

наиболее опасным и его нейтрализация должна обеспечиваться в первую

очередь. Обозначим во входном алфавите как x

элемент, соответствующий

наличию фактора Ц

. Выделим в выходном алфавите три элемента:

- решение УУ о нейтрализации фактора Ц

- таким будет выходной

сигнал детерминированного автомата при поступлении входного сигнала x

;

- решение УУ о нейтрализации фактора Ц

;

- отсутствие мер обеспечения безопасности объекта.

Пусть

- вероятности обнаружения и правильного определе-

ния характеристик соответственно Ц

и Ц

устройствами информационной

подсистемы. Тогда распределение вероятностей выходных сигналов вероят-

ностного автомата будет следующим:

   

 

1111 ц

pxnxynyPp 

   

 

1212 цц

ppxnxynyPp 

   

 

  

1313 цц

ppxnxynyPp 

   

 

 xnxynyPp

, 3 < l ≤ L.

Нетрудно убедиться, что







. Аналогично могут быть получены рас-

пределения вероятностей возможных решений УУ для всех предусмотренных

его алгоритмом ситуаций, которые и составят матрицу, задающую вместе с

множествами X и Y модель информационной подсистемы в форме вероят-

ностного автомата без памяти:

JLJJ

ppp







22221

11211



, (2.12)

где p

- вероятность формирования выходного сигнала y

при поступлении

входного сигнала x

Если найдены частные показатели эффективности устройств информа-

ционной подсистемы в форме вероятностей обнаружения и правильного

определения характеристик факторов внешней среды, полученная модель

позволяет определять вероятности правильного выбора мер обеспечения

безопасности объекта в различных ситуациях, то есть оценивать эффектив-

ность информационной подсистемы.

2.5. Модели с дискретными состояниями и непрерывным временем

Вводится конечное множество дискретных состояний системы

X=(x

,…,x

) таким образом, чтобы выполнялись следующие условия

- в любой рассматриваемый момент времени

система обязательно находится в одном из состоя-

ний, составляющих множество X;

- система не может одновременно находиться в

двух или более состояниях из множества X.

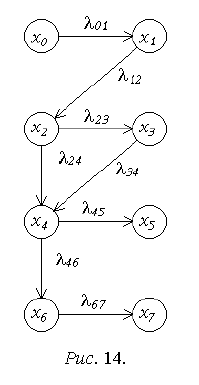
Логика процесса смены состояний описывает-

ся ориентированным графом (рис. 14), вершины

которого соответствуют состояниям системы, а

дуги – возможным переходам в другие состояния.

Отсутствие у вершины входящих дуг означает не-

возможность перехода в соответствующее состоя-

ние из какого-либо другого. Такие состояния назы-

ваются начальными, или источниками (x

на рис.

14). Отсутствие у вершины исходящих дуг означает

невозможность выхода из соответствующего со-

стояния. Такие состояния называются конечными,

или терминальными (x

и x

на рис. 14). При нали-

чии у вершин входящих и исходящих дуг соответствующие состояния назы-

ваются транзитивными (остальные состояния на рис. 14).

Процесс смены состояний рассматривается в непрерывном времени,

причем моменты времени, в которые происходят переходы системы из одно-

го состояния из множества X в другое, и длительности интервалов времени

пребывания системы в отдельных состояниях являются непрерывными слу-

чайными величинами.

Количественное описание такого процесса может быть обеспечено

только в среднем, применительно к многократному его повторению. Поэто-

му для описания состояния системы с дискретными состояниями и непре-

рывным временем используется закон распределения вероятностей дискрет-

ной случайной величины X(t):

----------------

Указанные требования являются достаточно очевидными и распространяются также

на F- и P-схемы. Однако здесь они имеют особое значение для формирования и понима-

ния используемого математического аппарата.

(t)=P(x(t))=x

. . .

(t)=P(x(t))=x

 











 ,0t

где каждая вероятность p

(t) представляет собой вероятность пребывания

системы в состояниии x

в момент времени t в условиях многократного по-

вторения рассматриваемого процесса смены состояний, начиная с t=0.

Кроме того, для количественного описания процесса с дискретными

состояниями и непрерывным временем могут использоваться переходные

вероятности. Переходная вероятность p

,) - это условная вероятность

того, что в момент времени t'= t

+  система окажется в состоянии x

, если в

момент времени t

она была в состоянии x

Процесс смены состояний называется марковским, или процессом без

последействия, если все его переходные вероятности зависят только от ука-

занных в их обозначении параметров: в каком состоянии x

система была в

момент времени t

и в какое состояние x

она должна попасть в момент вре-

мени t

+. Другими словами, все вероятностные характеристики марков-

ского случайного процесса "в будущем" (t>t

) зависят только от его теку-

щего состояния в момент t

и не зависят от того, каким образом и когда оно

достигнуто.

При построении математических моделей таких процессов используется

аппарат теории потоков случайных событий. Потоком случайных событий,

или случайным потоком, - называется последовательность моментов време-

ни {t

}, 0≤t

≤t

≤...≤t

≤… наступления некоторых событий, в которой

все t

(n=1,2,...) являются непрерывными случайными величинами. Поток

случайных событий можно представить также как последовательность интер-

валов времени между отдельными событиями {

}: 

–t

n–1

, n

≥

=0, где отдельные 

также являются непрерывными случайными величи-

нами. Понятие случайного потока предполагает невозможность регистрации

бесконечного числа событий на конечном интервале времени.

Если события, моменты наступления которых образуют случайный по-

ток П, являются неотличимыми друг от друга по каким-либо признакам, они

называются однородными, а поток П - однородным случайным потоком.

Назовем наиболее важные свойства случайных потоков.

1. Ординарность - невозможность одновременного наступления двух

или более событий. Если рассматривать вероятность наступления на некото-

ром малом интервале времени t после момента t более одного события

(t,t), то при ∆t→ 0 для ординарного потока она окажется бесконечно

малой величиной более высокого порядка, чем t:

 

lim









ttp

. (2.13)

2. Отсутствие последействия - количества событий, появляющихся на

непересекающихся конечных интервалах времени, являются независимыми

случайными величинами. Отметим, что данное свойство формально может

иметь место только при условии, что число событий, порождающих случай-

ный поток, не ограничено.

Если однородный поток обладает свойствами ординарности и отсутст-

вия последействия, он называется пуассоновским. Основная количественная

характеристика пуассоновского потока - интенсивность, или среднее число

событий в единицу времени:

 







lim

. (2.14)

Определим среднее число событий на малом интервале времени t как

математическое ожидание дискретной случайной величины с возмо жными

значениями 0,1,2,...,k,... и с учетом (2.13)

 

   

 

   

tttpttpttpttpttk  0,,2,1,0,

1210



где p

(t,t) - вероятность отсутствия событий на интервале t; p

(t,t) -

вероятность регистрации одного события на интервале t и так далее.

В результате получим:

 

ttp







lim

3. Стационарность - интенсивность случайного потока постоянна во

времени:

(t) =  = const.

Пуассоновский поток, обладающий свойством стационарности, назы-

вается простейшим.

Рассмотрим развитие марковского случайного процесса, граф которого

представлен на рис. 14, считая, что в начальный момент времени система

находится в состоянии x

. Поскольку момент времени t

перехода системы в

состояние x

является непрерывной случайной величиной, будем рассматри-

вать его как момент наступления первого события случайного потока П

характеризующегося интенсивностью 

(t). При этом принимается, что

после перехода в x

поток П

обрывается и возникает новый поток П

пе-

реходов из x

в x

с интенсивностью 

(t).

Рассматривая дальнейшее развитие процесса, будем использовать такой

принцип для всех состояний. Например, если система находится в состоянии

, существуют два потока П

с интенсивностью 

(t) и П

с интенсивно-

стью 

(t) переходов из x

соответственно в x

и x

. Если раньше наступит

первое событие потока П

, система перейдет в состояние x

и потоки П

прервутся. Если раньше наступит первое событие потока П

, система

перейдет в состояние x

, потоки П

и П

прервутся и возникнет поток П

переходов из x

в x

. Введенные таким образом случайные потоки П

назы-

вают потоками обрыва длительности состояний, а их интенсивности 

(t) -

интенсивностями обрыва длительности состояний или интенсивностями

смены состояний.

Чтобы случайный процесс в системе с дискретными состояниями и не-

прерывным временем, был марковским, необходимо и достаточно, чтобы

все потоки, переводящие систему из состояния в состояние, были пуассо-

новскими [40].

Перейдем к количественному описанию рассматриваемого процесса.

Пребывание системы в состоянии x

в некоторый момент времени

t'=t

+t следует рассматривать как сложное событие: C



, где A

- пребывание системы в состоянии x

в момент t;

- невыход из состояния

за интервал времени . Вероятность события C

определяется как произ-

ведение:

         















 ,

000

1000

tptpBPPtpCP A

Вероятность невыхода

 















tpBP

определим через вероятность

противоположного события - перехода из x

в x

- и используем интенсив-

ность случайного потока П

в соответствии с (2.14), считая  малой величи-

ной:

(t,)=1-p

(1)

(t,)=1-



(t)-0(),

где p

(1)

(t,) - вероятность наступления события потока П

на интервале .

Определим приращение вероятности p

за интервал времени  и найдем

ее производную:

            

















tpttptptp

tdp

0010

limlim





–

(t)p

(t). (2.15)

Составим теперь дифференциальное уравнение для вероятности транзи-

тивного состояния x

. Пребывание системы в состоянии x

в момент

t'=t

+ представляет собой сложное событие: C

B

A



, где

и A

- пребывание системы в момент t соответственно в состояниях x

; B

- переход из x

в x

на интервале ;

- невыход из состояния x

за

интервал времени . Вероятность события C

определяется с учетом его

состава следующим образом:

         

















11011

BPAPBPAPtpCP

p

(t)p

(t)+p

(t)p

(t)p

(t)p

(t)+p

(t)(1-p

(t)),

где p

(t,) - вероятность невыхода из x

за интервал времени ; p

(t,) -

вероятность противоположного события - перехода из x

в x

за интервал .

Аналогично предыдущему случаю, используя интенсивность случайного

потока П

, найдем производную вероятности p

     

          

















tpttpttp

tptp

tdp

1121010

limlim



(t)p

(t)– 

(t)p

(t). (2.16)

Аналогично (2.15), (2.16) при заданном графе смены состояний м огут

быть получены дифференциальные уравнения для вероятностей всех состоя-

ний марковского процесса с дискретными состояниями и непрерывным

временем, которые носят название уравнений А. Н. Колмогорова. В общем

случае система уравнений А. Н. Колмогорова имеет вид

 

       







iji

jji

ttptpt

tdp

, i=0,1,...,n; ji, (2.17)

где 

(t) - интенсивности случайных потоков, соответствующих исходящим

дугам i-й вершины; 

(t) - интенсивности случайных потоков, соответст-

вующих входящим дугам i-й вершины.

Для практического использования систему (2.17) необходимо допол-

нить условием нормировки:

 







. (2.18)

В ряде случаев система (2.17), решаемая изолированно от (2.18), может не

иметь решения.

При заданном начальном распределении вероятностей состояний p

(0),

i=0,1,...,n, отвечающем условию нормировки, система уравнений (2.17),

(2.18) позволяет определить распределение вероятностей состояний процесса

для любого произвольного момента времени t>0.

Для простейшего марковского процесса смены состояний, у которого

интенсивности 

постоянны, иногда практический интерес представляет

только финальное распределение вероятностей, соответствующее устано-

вившемуся режиму при t  . За исключением некоторых частных случаев,

оно может быть определено решением системы алгебраических уравнений,

получаемых из (2.17), если положить все производные равными нулю:







iji

jji

, i=0,1,...,n; ji, (2.19)

и заменить одно из полученных уравнений условием нормировки (2.18).

Определяемые по (2.18), (2.19) финальные вероятности оказываются

пропорциональны времени пребывания процесса в соответствующих со-

стояниях. Таким образом, установившийся простейший марковский процесс

смены состояний обладает эргодическим свойством (среднее по времени

совпадает со средним по множеству реализаций).

Рассмотрим наиболее часто используемые для решения практических

задач модели процессов и систем с дискретными состояниями и непрерыв-

ным временем. На рис. 15 показаны графы процессов "чистой гибели" (а),

"чистого размножения" (б), "гибели и размножения" (в). В частных случаях