Емельянов В.Ю. Методы моделирования стохастических систем управления

Подождите немного. Документ загружается.

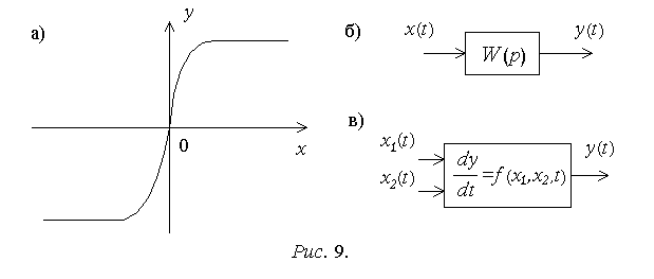
математической модели системы нелинейной статической характеристикой

(рис. 9,а), позволяющей для любого значения входного сигнала x получить

соответствующее значение выходного сигнала y. Такая форма описания

предполагает, что входные и выходные переменные могут меняться во вре-

мени, но для любого момента времени t значение "выхода" Y(t) зависит

только от значения “входа" X(t) в тот же момент времени. Другими слова-

ми, статические модели не учитывают предысторию описываемого процес-

са.

Динамические модели учитывают развитие процессов во времени, то

есть их предысторию. Их общий вид: Y(t)=f({Y(τ),τ<t},{X(τ),τ ≤ t}). Таким

образом, значение "выхода" Y здесь может зависеть и от своих значений в

предшествующие моменты времени, и от значений "входа" в рассматривае-

мый и предшествующие моменты времени. Так если рассматривается пре-

образование усилителем быстро изменяющихся сигналов, приходится учи-

тывать инерционность усилителя, и его модель задается в одной из форм,

представленных на рис. 9,б,в.

Динамические модели применяются для описания как отдельных эле-

ментов, так и систем в целом. Ниже им уделяется основное внимание.

Дискретизация моделей систем может осуществляться путем перехода к

дискретному времени или введения дискретного множества состояний. В

связи с этим различаются следующие варианты.

В непрерывных моделях, или D - схемах, множество состояний системы

и время являются непрерывными. Состояние модели описывается вектором

фазовых переменных, или переменных состояния,

X(t)=(x

(t),x

(t),…,x

(t)). Модель задается в форме системы диффе-

ренциальных уравнений, чаще всего системы уравнений 1-го порядка:

 

    

ttUtX

,,

, i=1,2,…,n,

(t)=ψ

(X(t)), j=1,2,…,m, (2.1)

где U(t)=(u

(t),u

(t),…,u

(t)) – вектор входных переменных; y

– выход-

ные переменные системы. Помимо дифференциальных уравнений, для по-

строения и анализа непрерывных моделей систем управления используются

передаточные функции, частотные характеристики и др. Математический

аппарат исследования непрерывных моделей достаточно хорошо освещен в

технической литературе [3, 11, 32, 39].

Если рассматриваются непрерывное множество состояний и дискрет-

ное время, строятся модели дискретных, или импульсных, систем. При этом

предполагается возможность изменения значений всех или некоторых пере-

менных состояния в моменты времени, разделенные некоторым тактом или

шагом T

. Непрерывные функции времени x(t) здесь заменяются решетча-

тыми функциями x(n), n= 0,1,…, причем

1 Tn 

. Для таких моделей ис-

пользуется аппарат разностных уравнений, импульсных передаточных функ-

ций и псевдочастотных характеристик, также детально разработанный в рам-

ках теории управления [3, 4, 11, 32].

Модели с дискретными состояниями и дискретным временем строятся

на основе теории конечных автоматов и марковских цепей [1, 37, 42]. При

построении модели в форме конечного автомата вводятся дискретные ко-

нечные множества: состояний Z, входных сигналов X и выходных сигналов Y.

Если рассматривается детерминированный конечный автомат (F-схема),

задаются функция переходов  (z,x), формализующая правила смены со-

стояний автомата, и функция выходов, (z,x), формализующая правила

формирования выходного сигнала на очередном такте работы автомата.

Модели с дискретными состояниями и непрерывным временем строят-

ся на основе теории марковских процессов или Q-схем [1, 9, 37, 40]. Задается

дискретное конечное множество состояний системы X=(x

,…,x

Рассматриваются только случайные процессы смены состояний. Для качест-

венного описания процесса используется граф смены состояний, для коли-

чественного описания – переходные вероятности или интенсивности смены

состояний (рис. 10).

Для сложных динамических систем применяются более сложные спосо-

бы дискретизации. Один из вариантов – построение модели динамической

системы со случайной структурой [19].

Модель строится в непрерывном

времени. Вводится дискретное конеч-

ное множество состояний системы

Y=(y

,…,y

), которые называют

также фазами движения или режима-

ми работы. Каждому состоянию соот-

ветствует определенный вектор не-

прерывных фазовых переменных

(l)

(t) =

(l)

(t),x

(l)

(t),…,x

(l)

(t)),

l=1,2,...,L,

и система дифференциальных уравнений вида (2.1):

 

   

 

lll

yttUtXf

tdx

,,

(t) = ψ

(l)

(t)), i=1,2,...,n; j=1,2,...,m; l=1,2,...,L. (2.2)

Частным случаем модели со случайной структурой является модель

динамической разрывной системы (схема ДРС), в которой векторы X

(l)

имеют одинаковую размерность для всех фаз движения [13]. Схема ДРС мо-

жет рассматриваться как двухуровневая комбинированная схема построения

модели, где на нижнем уровне используется D-схема, на верхнем – одна из

дискретных схем.

По характеру моделируемых процессов различают детерминированные

и стохастические модели. Если для характеристик внешних воздействий и всех

элементов моделируемой системы могут рассматриваться фиксированные

значения, а процессы в системе подчиняются известным жестким законо-

мерностям, строят детерминированные модели. В случаях, когда требуется

учет случайных внешних воздействий, значений параметров системы или

начальных условий, строят стохастические модели.

Так, если правила смены состояний конечного автомата являются жест-

кими, используется детерминированная F-схема. Стохастический конечный

автомат называется вероятностным автоматом (P-схемой). У вероятностного

автомата правила смены состояний не являются жесткими. Для каждого воз-

можного сочетания состояния автомата и входного сигнала задается распре-

деление вероятностей переходов в другие состояния [29].

В свою очередь, на основе D-схемы могут быть построены как детер-

минированные, так и разнообразные стохастические модели.

Существенное значение для выбора математического аппарата модели

имеет нестационарность как самой системы, так и исследуемого процесса.

Нестационарные модели, как правило, не допускают получения результата

путем аналитических преобразований и требуют пошагового решения сис-

тем уравнений приближенными методами.

Для детерминированной задачи стационарная модель может быть по-

строена для любой стационарной системы, то есть системы, параметры ко-

торой не изменяются на моделируемом интервале времени.

Для стохастической задачи, где учитываются случайные внешние воз-

действия, стационарная модель и соответствующий математический аппарат

могут использоваться даже для стационарной системы только при расчете

установившегося процесса и при условии, что внешние воздействия стацио-

нарны.

Линейность или нелинейность модели определяется необходимостью

учета нелинейности отдельных элементов моделируемой системы. Приве-

денные выше для D-схемы уравнения (2.1) задают нелинейную модель. Ли-

нейная D-схема будет иметь вид

 

       

tUtBtXtA

tdX



, Y(t)=C(t)X(t),

где A, B и C – матрицы коэффициентов.

Рассмотрим подробнее некоторые математические схемы, применяе-

мые при построении моделей сложных стохастических систем, но не изучае-

мые обычно в рамках курса "Теория автоматического управления".

2.3. Детерминированные конечные автоматы и их применение при

построении моделей сложных систем

Математическая F-схема, или детерминированный автомат [42], являет-

ся удобной формой описания логических закономерностей развития процес-

сов в системе, но не учитывает фактор случайности. Поэтому она обычно

используется для моделирования подсистем контроля и управления и позво-

ляет решать задачи разработки, проверки и оценки качества реализуемых

ими алгоритмов принятия решения, выбора закона управления или измене-

ния структуры системы.

F-схема задается в форме следующей совокупности:

F=(X,Z,Y,,), (2.3)

где Z=(z

,…,z

) – множество состояний, или внутренний алфавит;

X=(x

,…,x

) – конечное множество входных сигналов, или входной

алфавит; Y=(y

,…,y

) – конечное множество выходных сигналов, или

выходной алфавит; =(z,x) - функция переходов, описывающая законо-

мерности смены состояний; =(z,x) – функция выходов, описывающая

закономерности формирования выходных сигналов. Если множество состоя-

ний является конечным, автомат (2.3) называется конечным. Конечный авто-

мат представляет собой абстрактную математическую схему. Поэтому при-

рода состояний и сигналов безразлична.

Теория автоматов получила свое первоначальное развитие в тесной

связи с разработкой логических схем цифровой вычислительной техники. Для

ее применения при построении моделей систем управления целесообразно

уточнить смысл некоторых терминов.

С позиций теории управления конечный автомат может рассматривать-

ся как "черный ящик" с одним входом и одним выходом. На вход подается

сигнал x, а с выхода снимается сигнал y (рис. 11). Сигналы x и y могут при-

нимать только фиксированные значения. Возможные значения входного

сигнала образуют дискретное конечное множество X, значения выходного –

дискретное конечное множество Y.

Другая, расширенная, трактовка понятия автомата допускает наличие

нескольких входов или выходов. Так например, допустим наличие у автомата

M входных каналов с собственными алфавитами X

(m)

 

,...,

 

Тогда алфавит X вводится как произведение алфавитов:

X=X

(1)

×X

(2)

×…×X

(M)

, то есть символами алфавита X объявляются все воз-

можные сочетания элементов алфавитов X

(m)

по одному из каждого. Коли-

чество элементов в X в результате составит





Аналогичный прием может быть использован в предположении, что

имеется несколько выходных каналов. В любом случае сохраняется общий

вид представления автомата в форме (2.3).

Далее будет использоваться терминология, принятая в теории автом а-

тов, которую следует воспринимать с учетом этих замечаний.

Процесс в конечном автомате рассматривается в дискретном времени,

единицей измерения которого является такт. В течение такта значения всех

сигналов сохраняются постоянными. При наступлении следующего такта

может измениться входной сигнал x. В зависимости от его значения в соот-

ветствии с жесткими правилами, заданными функцией переходов, может

измениться или сохраниться состояние автомата z. Одновременно в соответ-

ствии с жесткими правилами, заданными функцией выходов, формир уется

новый выходной сигнал y. Величина такта не обязательно является постоян-

ной (рис. 11).

Рассмотрим простейшие и наиболее широко используемые виды ко-

нечных автоматов.

1. Автомат Мили имеет функции переходов и выходов следующего ви-

да:

z[n+1]=(z[n],x[n]), y[n]=(z[n],x[n]), (2.4)

где n=0,1,2,... – номер такта. Таким образом, в автомате Мили новое состоя-

ние и выходной сигнал выбираются в зависимости от сочетаний текущего

состояния и входного сигнала.

Рассмотрим пример автомата Мили, используя для задания функций

переходов и выходов табличный, графический и матричный способы.

При табличном способе для функции переходов задается таблица пере-

ходов (табл. 1), а для функции выходов – таблица выходов (табл. 2). Строки

таблиц соответствуют элементам входного алфавита, а столбцы – элементам

внутреннего алфавита. Позиция таблицы переходов, соответствующая i-му

столбцу и j-й строке, – это новое состояние, в которое переходит автомат,

если в момент прихода входного сигнала x

он находился в состоянии z

, а

аналогичная позиция таблицы выходов – формируемый при этом выходной

сигнал.

Та б л ица 1

Та б л ица 2

Таблица переходов автомата Мили

Таблица выходов

Входные

сигналы

Состояния

Входные

сигналы

Состояния

При матричном способе обе функции задаются одной матрицей соеди-

нений C размерностью I×I, строки которой соответствуют исходным со-

стояниям z[n], столбцы - состояниям на следующем такте z[n+1]. Элемен-

ты матрицы задаются в виде дроби, в числителе которой указывают входной

сигнал, вызывающий соответствующий переход, а в знаменателе - форми-

руемый при таком переходе выходной сигнал. Вместо элементов, соответст-

вующих невозможному для данного автомата переходу, ставится прочерк:





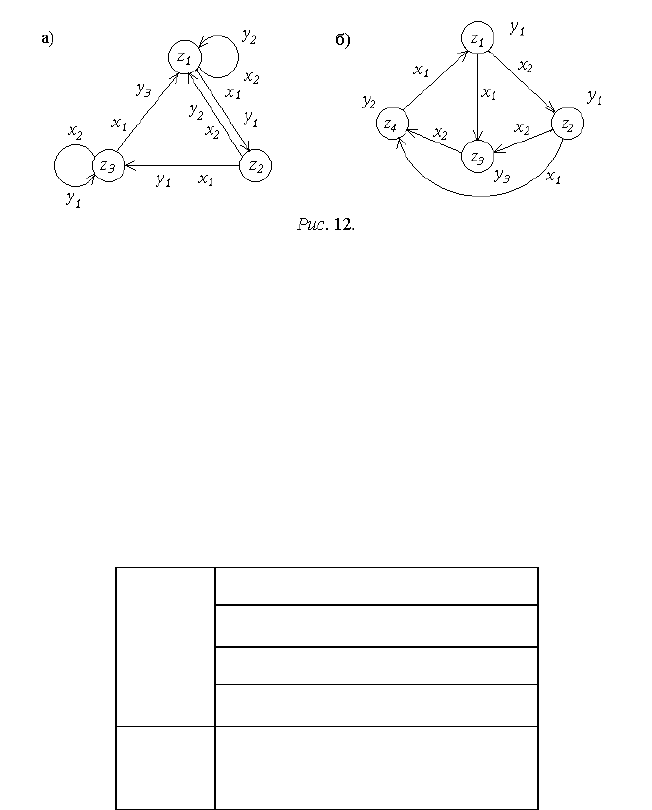
При графическом способе автомат Мили задается графом (рис. 12,а),

вершины которого соответствуют возможным его состояниям. Каждая вер-

шина имеет J исходящих дуг, соответствующих вариантам смены или сохр а-

нения состояний при различных входных сигналах x

(j=1,2,...,J). Около

каждой дуги указывают соответствующие ей входной и выходной сигналы.

Отметим, что количества позиций таблицы переходов, позиций таблицы

выходов, задаваемых элементов матрицы соединений и дуг графа для автома-

та Мили одинаковы.

2. У автомата Мура функции переходов и выходов имеют вид

z[n+1]=(z[n],x[n]), y[n]=(z[n]). (2.5)

Таким образом, здесь новое состояние определяется аналогично авто-

мату Мили, а выходной сигнал зависит только от текущего состояния автома-

та. Способы задания автомата Мура также рассмотрим на примере.

Автомат Мура может задаваться таблицей переходов (табл. 3), которая,

за исключением верхней строки, составляется аналогично табл. 1. В верхней

строке табл. 3 указываются выходные сигналы, связанные с элементами вто-

рой строки в соответствии с функцией выходов.

Та б л ица 3

Таблица переходов автомата Мура

Выходные сигналы

Входные

сигналы

Состояния

Другие варианты задания автомата Мура – граф (рис. 12,б) или матрица

соединений C и вектор выходов Y:





Y 

. (2.6)

3. В автономном автомате отсутствуют входные сигналы:

F=(Z,Y,,), z[n+1]=(z[n]), y[n]=(z[n]). (2.7)

Его удобнее всего задать графом, у которого каждой вершине (состоянию

автомата) соответствует одна и только одна выходная дуга и определенный

выходной сигнал, или соответствующей таблицей.

Следует отметить, что в любом конечном автономном автомате состоя-

ния и выходные сигналы неизбежно начнут периодически повторяться, на-

чиная с некоторого такта. Длина такого периода не превышает количества

состояний автомата, а начальное состояние влияет только на номер такта,

начиная с которого наступает периодический процесс.

4. Автомат без памяти обеспечивает однозначное отображение входно-

го алфавита X в выходной Y:

F=(X,Y,), y[n]=(x[n]) (2.8)

и может быть задан вектором Y вида (2.6), размерность которого соответст-

вует размерности множества X, или соответствующей таблицей.

5. В автомате без выхода отсутствуют выходные сигналы:

F=(X,Z,), z[n+1]=(z[n],x[n]). (2.9)

Его функция переходов задается в форме таблицы, графа или матрицы.

В качестве примера рассмотрим автоматную модель устройства управ-

ления (УУ) системы обеспечения безопасности движущегося объекта. В

зависимости от состояния внешней среды, информация о которой поступает

от устройств информационной подсистемы, УУ в соответствии с жестким

алгоритмом определяет необходимые меры безопасности (маневр, останов-

ка, активное воздействие на внешнюю среду и др.) и формирует команды

управления для устройств исполнительной подсистемы.

Будем рассматривать каждый физический вход УУ, на который посту-

пает сигнал от какого-либо устройства информационной подсистемы, как

один из M входных каналов автомата. Входной алфавит автомата X введем

как произведение алфавитов входных каналов: X=X

(1)

×X

(2)

×…×X

(M)

. Оче-

видно, реальные сигналы от различных устройств могут быть как дискретны-

ми, так и непрерывными и иметь разные диапазоны изменения. Независимо

от этого набор элементов в абстрактном m-м входном алфавите выбирается в

соответствии с количеством J

значений или диапазонов сигнала, различае-

мых УУ при выработке решения.

Элементы выходного алфавита Y=(y

,…,y

) будут соответство-

вать вариантам мер безопасности, предусмотренных алгоритмом УУ.

В зависимости от особенностей алгоритма УУ задается внутренний ал-

фавит Z=(z

,…,z

) и строится автомат вида (2.3), (2.8) или (2.9). В про-

стейшем случае строится автомат без памяти (2.8).

2.4. Вероятностные автоматы и марковские цепи

Вероятностный автомат (P-схема) - это конечный автомат, в котором за-

кономерности смены состояний и формирования выходного сигнала имеют

статистический характер [22, 29].

Пусть заданы множество входных сигналов автомата X размерностью J,

множество состояний Z размерностью I и множество выходных сигналов Y

размерностью L. Введем новое множество G, элементами которого являются

пары x

, и новое множество Ф, элементами которого являются пары z

Очевидно, множество G будет иметь размерность K=IJ, а множество Ф -

размерность S=IL.

Для вероятностного автомата любой элемент множества G индуцирует

на множестве Ф дискретный закон распределения (p

,…,p

). Авто-

мат может быть задан совокупностью

P=G,Ф,В=X,Z,Y,В, (2.10)

где B=║p

║- матрица переходных вероятностей размерностью K×S.

Элементы матрицы B должны отвечать следующим условиям:

≤

1, k =1,2,...,K; s =1,2,...,S;







, k =1,2,...,K.

Вместо матрицы B может быть задана таблица переходных вероятно-

стей. Строки матрицы B и таблицы переходных вероятностей соответствуют

элементам множества G, столбцы - элементам множества Ф.

Таким образом, если в детерминированном автомате заданной последо-

вательности входных сигналов x(1),x(2),…,x(n) будет соответствовать оп-

ределенная жесткая последовательность выходных сигналов

y(1),y(2),…,y(n), то в вероятностном автомате такая последовательность