Ellis A.M., Feher M., Wright T. Electronic and Photoelectron Spectroscopy: Fundamentals and Case Studies

Подождите немного. Документ загружается.

5 Molecular vibrations

Internuclear separation, r

v = 0,

v = 1,

v = 2,

v = 3,

v = 4,

v = 5,

V(r)

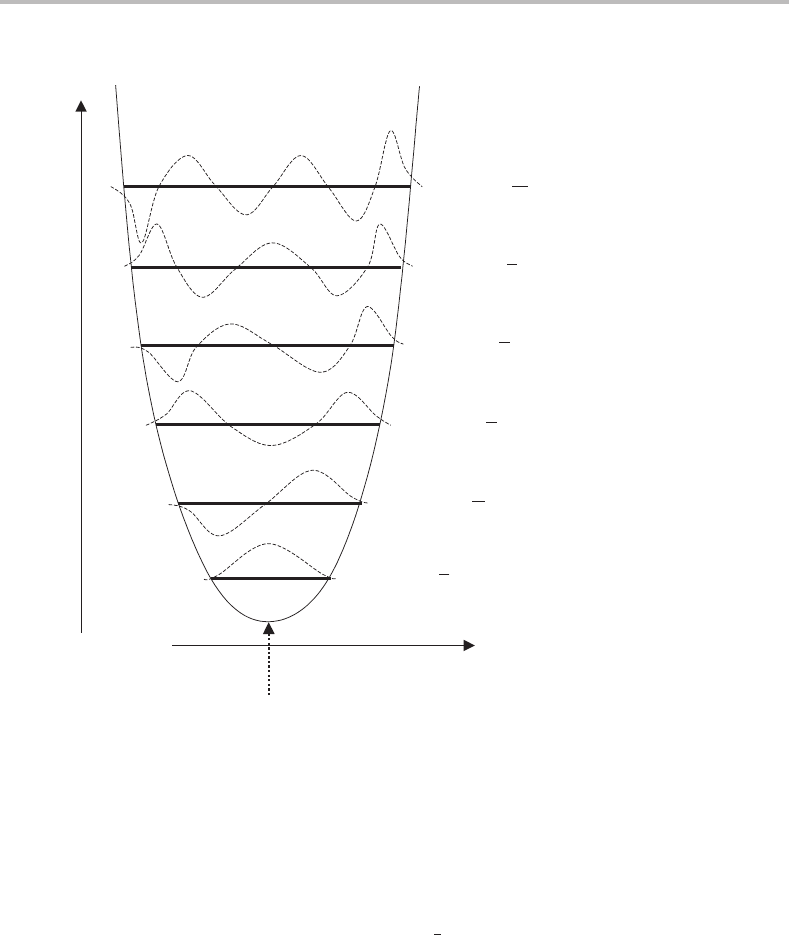
Figure 5.1 Plot showing the parabolic potential energy curve of a diatomic simple harmonic oscillator.

Superimposed on the curve are the ﬁrst few energy levels expected for a quantized harmonic oscillator,

each being labelled by a unique value of the vibrational quantum number v. Also shown (dashed lines)

are the corresponding vibrational wavefunctions.

Substituting for F in equation (5.1) using the expression in (5.2) followed by integration

gives

V =

(5.3)

If it is assumed that a diatomic molecule is also subject to Hooke’s law, then the potential

energy due to distortion will be given by equation (5.3)where x = r − r

, r is the inter-

nuclear separation, and r

is the equilibrium bond length. A plot of V versus r is shown in

Figure 5.1. The potential energy curve is parabolic, being symmetrical about equilibrium

(where r = r

). If one imagines the bond being stretched to a certain displacement and

then released, the stored potential energy is progressively converted to kinetic energy as

the bond shortens until at r

all of the energy is kinetic. The system then passes through

the equilibrium position and gradually converts the kinetic energy back to potential energy

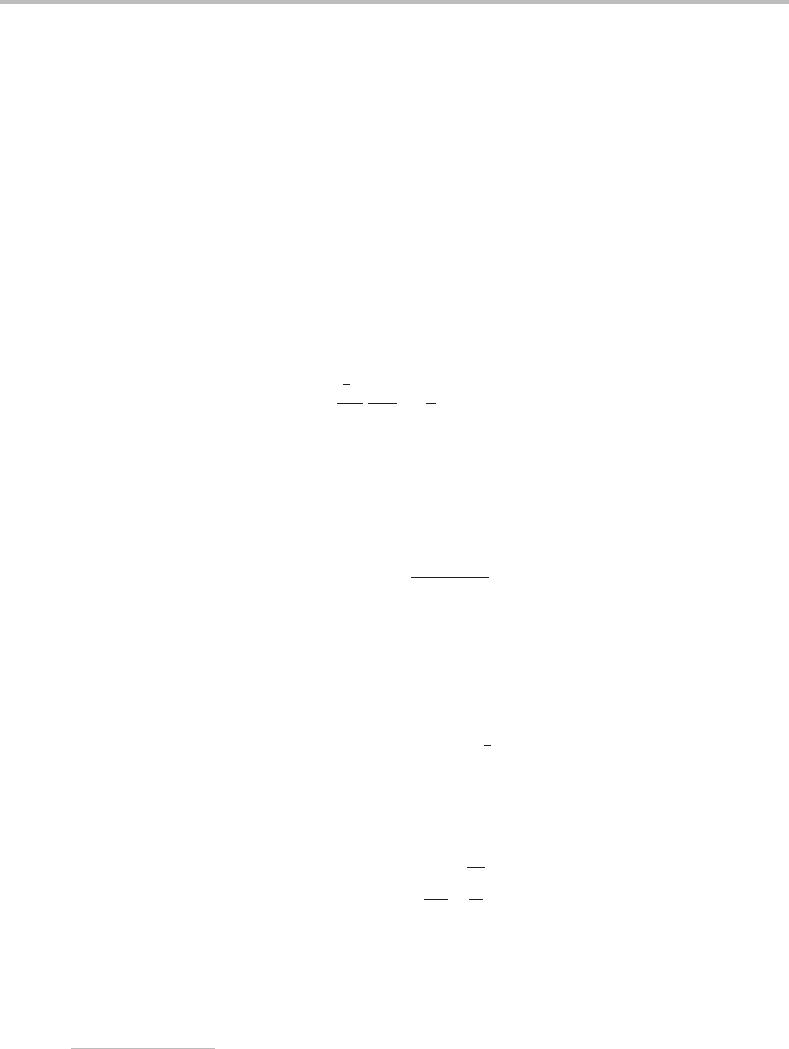
26 Foundations

as the bond is compressed. Once the kinetic energy has all been converted into potential

energy, the molecule is at its inner turning point and then reverses its motion by progressively

stretching the bond again. The total amount of energy in this vibrational motion, potential +

kinetic, is constant and is referred to as the vibrational energy.

5.1.2 The quantum mechanical harmonic oscillator: vibrational energy levels

The above discussion is a classical view of vibrational motion. In the classical world a vibrat-

ing diatomic molecule may have any vibrational energy. However, once quantum mechanics

is taken into account this is no longer the case. To determine the quantum mechanical

energies in the harmonic oscillator limit, the potential energy expression in (5.3)issubsti-

tuted into the Schr¨odinger equation to obtain the following:



−



ψ = Eψ (5.4)

Equation (5.4)isonly valid when one of the atoms is essentially of inﬁnite mass, in which

case it is only the lighter atom, of mass m,which moves in a vibration. In reality no atom

is inﬁnitely heavy and therefore to describe vibrational motion about the centre-of-mass,

m is replaced in (5.4) with the reduced mass µ where

µ =

+ m

(5.5)

and m

are the masses of the two atoms. Equation (5.4) can be solved, although it

is a rather involved process; we focus here solely on the results.

It is found, not surprisingly, that the energy is now quantized. The allowed vibrational

energies are given by the expression

= hω



v +



(5.6)

where ω

is the harmonic vibrational frequency (in Hz),

and v is the vibrational quantum

number,which can have the values 0, 1, 2, 3, . . . The vibrational frequency depends on

both the bond force constant and the reduced mass in the following fashion:

2π



(5.7)

Equation (5.6) shows that the quantized harmonic oscillator consists of a series of equally

spaced energy levels, the separation between adjacent levels being hω

. This is illustrated

in Figure 5.1. According to equation (5.7), ω

will increase as the bond force constant

By specifying atomic displacements relative to the centre-of-mass, no overall translational energy of the molecule

is included in a calculation of the vibrational energy. In a centre-of-mass system, if the two atoms have different

masses, a displacement x involves the lighter atom moving further than the heavier atom (which moves in the

opposite direction) such that the centre-of-mass remains stationary.

The subscript on ω

indicates that vibration is, rather obviously, about the equilibrium position. It is customary to

retain it when referring to diatomic molecules but for polyatomic molecules the e subscript will be omitted and

instead the subscript will be a number designating a particular vibrational mode (see Section 5.2.1).

5 Molecular vibrations

increases. Stronger bonds tend to be stiffer bonds and therefore vibrational frequencies

normally increase with increasing bond strength. The reduced mass acts in the opposite

direction, with an increase in µ leading to a decrease in hω

.Itshould also be noted that

even in the lowest energy level, corresponding to v = 0, the vibrational energy is non-

zero. This residual energy is known as the zero point energy, and plays a celebrated role in

quantum mechanics [1].

It is more usual to employ wavenumber units than energies when dealing with vibrational

transitions in spectroscopy. Equation (5.6) can be re-written as a vibrational term value,

G(v), given by

G(v) = ω



v +



(5.8)

where ω

is now interpreted as the harmonic vibrational wavenumber, usually expressed in

−1

, and therefore G(v) has the same units. Term values will be used extensively throughout

this book.

5.1.3 The quantum mechanical harmonic oscillator: vibrational

wavefunctions

Full solution of the Schr¨odinger equation (5.4) also yields the vibrational wavefunctions in

addition to energies. These have the mathematical form

= N

(η)exp(−η

/2) (5.9)

where N

is a normalization constant and η = 2π (µcω

/h)

(r − r

). Note that η is directly

proportional to the displacement (r − r

). The quantity H

(η)isaHermite polynomial in

the coordinate η, and the ﬁrst few Hermite polynomials are

(η) = 1

(η) = 2η

(η) = 4η

− 2

(η) = 8η

− 12η

(η) = 16η

− 48η

+ 12 (5.10)

We can therefore write down the wavefunctions for the ﬁrst few vibrational levels of a

diatomic molecule as follows:

= N

exp(−η

/2)

= 2N

η exp(−η

/2)

= N

(4η

− 2) exp(−η

/2)

= N

(8η

− 12η)exp(−η

/2)

= N

(16η

− 48η

+ 12) exp(−η

/2) (5.11)

Although the above functions may look quite cumbersome, they have a simple form when

plotted, as shown in Figure 5.1.Anumber of important conclusions arise. First, the prob-

ability of the molecule being at any particular internuclear separation is given by ψ

28 Foundations

the particular value of r − r

. Thus for v = 0 quantum mechanics predicts that the most

probable internuclear separation is r

. This is counterintuitive when one thinks of a spring,

since a vibrating spring will spend most of its time in the region of the two turning points

and is moving at its fastest at the equilibrium position! Note also that there is some ‘leakage’

of the wavefunction outside of the harmonic oscillator potential well, a phenomenon that

is impossible in the classical case. This ‘leakage’ grows in importance as the vibrational

energy is increased.

For levels v = 1 and higher, nodes appear in the wavefunction and indeed the number

of nodes is equal to the vibrational quantum number. As v increases, the wavefunction

progressively heads towards behaviour that is anticipated classically, i.e. the most probable

internuclear separations shift towards the turning points, with the probability of ﬁnding the

molecule at the equilibrium separation becoming rather small.

5.1.4 The anharmonic oscillator

The justiﬁcation for treating a vibrating diatomic molecule like a quantized vibrating

spring is that the harmonic oscillator model works rather well. Spectroscopic measurements

demonstrate that the separation between adjacent pairs of vibrational levels is indeed approx-

imately constant, as equation (5.6) predicts. However, if we look more closely at experi-

mental data, and if we think more clearly about the implications of the potential well shown

in Figure 5.1 we conclude that the harmonic oscillator model is only an approximation and

there are circumstances where its failure can be very serious.

The most obvious deﬁciency is that no allowance is made for the fact that any bond, or

for that matter any spring, will eventually break when sufﬁciently stretched. The harmonic

oscillator potential energy curve is inﬁnitely deep, which would lead to the nonsensical

conclusion that a chemical bond is inﬁnitely strong.

Qualitatively, the potential energy curve of a real diatomic molecule would be expected

to have the same shape as that shown in Figure 5.2.Todetermine the pattern of vibrational

energy levels for such an oscillator, which is now referred to as anharmonic because of

the asymmetry of the potential energy curve, a mathematical form for the potential energy

is needed, which can be substituted into the Schr¨odinger equation (5.4)inplace of the

harmonic potential (5.3). A number of different mathematical functions give rise to a curve

of similar shape to that shown in Figure 5.2 but the most widely used is the Morse potential

function,which has the form

V = D

{1 − exp[−a(r −r

)]}

(5.12)

where D

is the dissociation energy of the molecule, measured from the bottom of the

potential well. The quantity a is a constant that varies from one molecule to another (and

one electronic state to another), as does D

Solution of the Schr¨odinger equation with the potential in equation (5.12)gives

= hω



v +



− hω



v +



(5.13)

5 Molecular vibrations

V(r)

A + B

Internuclear distance, r

Figure 5.2 Morse potential energy curve for a diatomic molecule AB with quantized vibrational

energy levels superimposed. Two different deﬁnitions of dissociation energies are shown, dissociation

energy D

measured from the bottom of the potential well, and D

, measured from the zero point

level. Since all molecules must have at least the zero point vibrational energy, D

is the more useful

quantity.

where ω

is in Hz or, expressed as a term value,

G(v) = ω



v +



− ω



v +



(5.14)

with ω

in wavenumbers. Notice that the ﬁrst term on the right-hand side of (5.13)isidentical

to the harmonic oscillator energy expression (5.6). The second term differs in two ways.

First, it depends on the square of v +

, and second it contains the dimensionless quantity x

which is known as the anharmonicity constant.For almost all diatomics the anharmonicity

constant is small, typically <0.01, and therefore if v is small the second term in (5.13) and

(5.14), the anharmonic correction, is also small. The harmonic oscillator approximation is

therefore a good one for vibrational energy levels near the bottom of the potential well.

However, the anharmonic correction quickly grows in importance as v increases, due to

the quadratic dependence on v +

. Furthermore, the fact that the anharmonic correction is

subtracted from the harmonic term means that adjacent vibrational levels get closer together

as the vibrational ladder is climbed, and in the limit that dissociation is reached the energy

levels form a continuum. This convergence of energy levels is illustrated in Figure 5.2.

5.1.5 Vibrations in different electronic states

A Morse potential of the type shown in Figure 5.2 and equation (5.12)isnormally a good

approximation to the vibrational potential energy of a real diatomic molecule. However,

30 Foundations

Table 5.1 Spectroscopic constants for the ground

and ﬁrst excited electronic states of CO

Parameter X





/Å 1.1281 1.2351

/cm

−1

2170.21 1515.61

/cm

−1

13.46 17.25

/cm

−1

90 230 25 160

let us think more closely about the factors that determine the precise form of the Morse

potential for a particular electronic state of a molecule.

As an example consider CO, which has the ground electronic conﬁguration

1σ

2σ

3σ

4σ

5σ

1π

and therefore has a



ground electronic state.

The ﬁrst four

σ orbitals are bonding/antibonding pairs, and so have the effect of cancelling each other out

in a bonding sense. However, the 5σ and 1π orbitals are bonding orbitals and since both

are full the molecule is held together by a triple bond in very much the same way as N

(which is isoelectronic with CO). The carbon and oxygen atoms will therefore be strongly

bound together in the



ground electronic state, and indeed the dissociation energy D

1074 kJ mol

−1

(90 230 cm

−1

), which is very large. In addition, a strong bond would be

expected to yield a relatively short equilibrium bond length and a relatively high vibrational

frequency (since the bond force constant will be large).

Now suppose that an electron is excited from the 5σ MO to the vacant 2π MO. Providing

the spin of this electron maintains the same orientation, the excited state will be a

 state.

The 2π MO is strongly antibonding, so the dissociation energy should decrease signiﬁcantly.

Concomittantly, the vibrational frequency should also decrease and the equilibrium bond

length should increase. This is precisely what is found experimentally, as illustrated by the

data for CO collected in Table 5.1.

In the general case, different shaped potential energy curves are expected for different

electronic states. The minimum of each of these curves represents the pure electronic energy

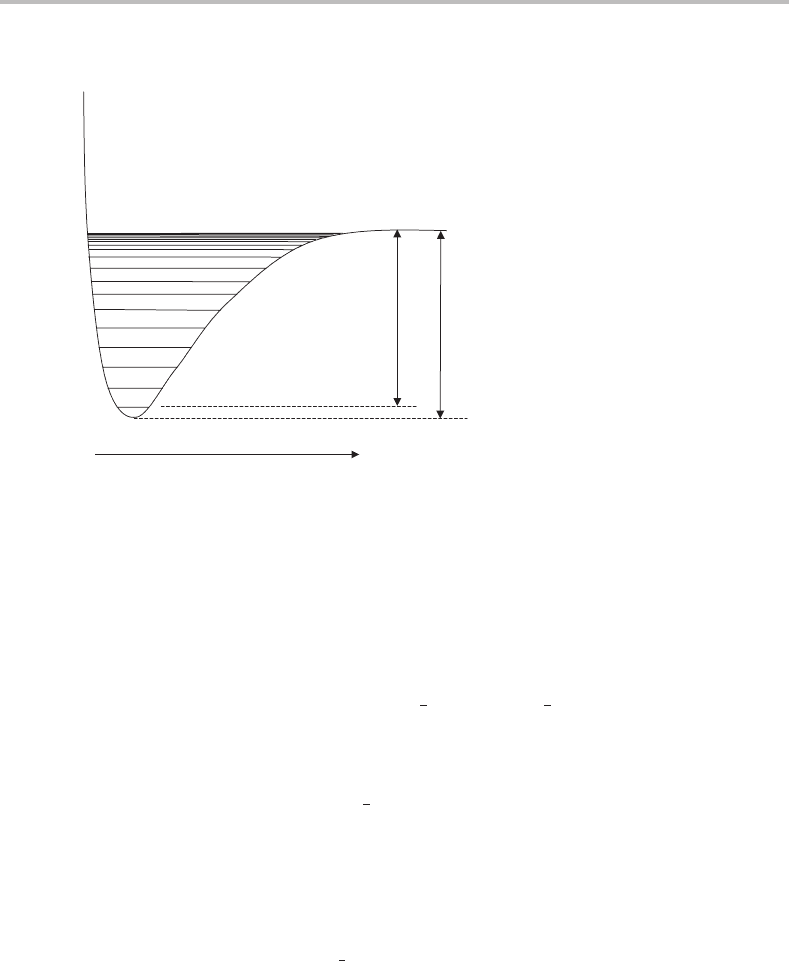
of the state. A diagram showing the potential energy curves for the two states of CO that

we have just considered is shown in Figure 5.3. This ﬁgure is rather simple, but if every

potential energy curve of the known electronic states of CO were shown on this diagram

it would look very complicated, particularly at high energies. This point is illustrated by

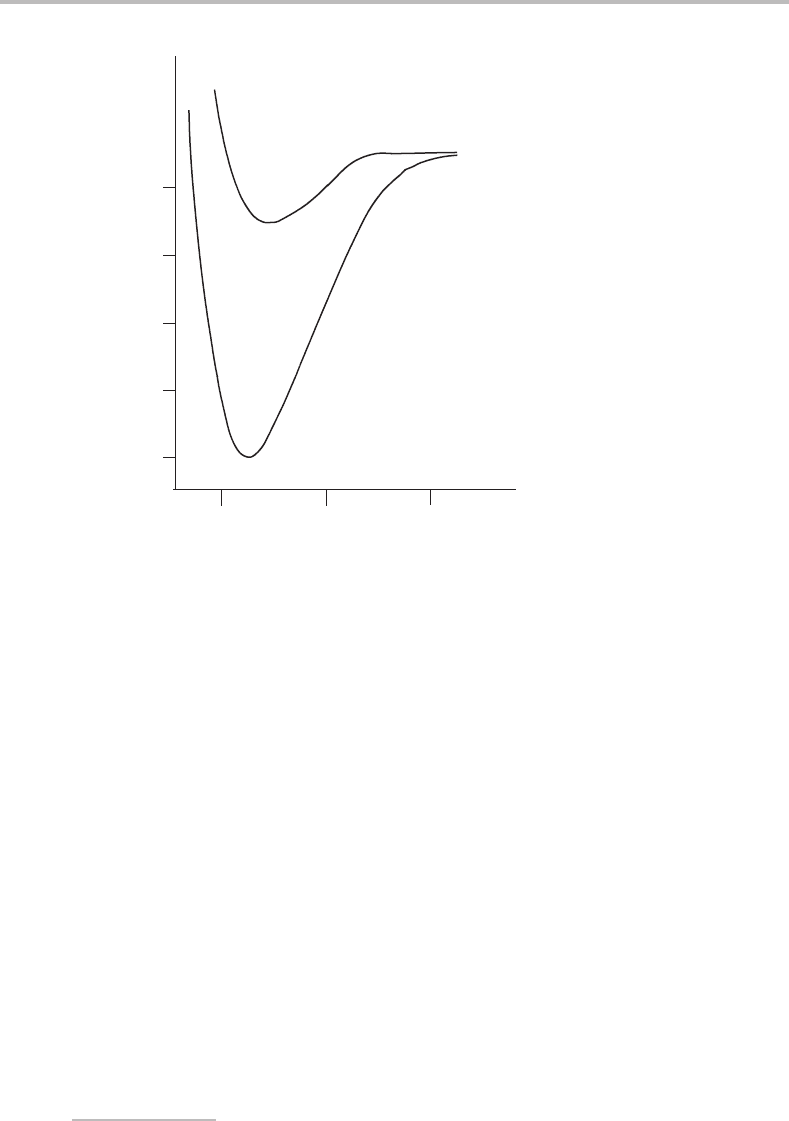
Figure5.4,which showssome of the potential energy curves of PbH, a free radical. Figure5.4

clearly shows that a molecule in some particular electronic state need not dissociate to the

ground state atoms. If this were not true, then it would be impossible to have a bound

state with an electronic energy above that of the two ground state atoms, which would be

contrary to experimental observations. The factors that determine which electronic states of

the atoms correlate with which molecular electronic state is beyond the scope of this book

(see [2]).

Strictly speaking the σ MOs of CO should be labelled σ

to distinguish them from σ

−

symmetry. However, since

all of the σ MOs have σ

symmetry it is common to drop the superscript.

5 Molecular vibrations

P) + O(

1.0

1.5 2.0

r/Å

Wavenumber/cm

−1

20 000

40 000

60 000

80 000

Figure 5.3 Potential energy curves for the X



and the A

 states of CO. Clearly the former is

far more strongly bound than the latter. Both of these states correlate with the lowest dissociation

asymptote, formation of ground state C and O atoms.

5.2 Polyatomic molecules

5.2.1 Normal vibrations

The vibrating diatomic molecule is relatively easy to describe since it has only one bond,

and therefore only one vibrational mode. The situation is clearly more complicated for

polyatomicmolecules, since there is more than one bond that may be stretched/compressed,

and there are also bond angles that can be changed by vibrations. At ﬁrst sight a pessimist

might conclude that it would be difﬁcult, if not impossible, to solve the quantum mechanics

of polyatomic vibrations. However, this is not the case, although there are indeed additional

complications.

It is helpful to focus on small molecules to bring out the key features applicable to more

complicated molecules. In fact we will consider three triatomic molecules, CO

, OCS, and

O, as an illustration.

It is obvious that a vibrating bond will undergoboth stretching and compression as it oscillates about the equilibrium

position. However, it is pedantic to keep referring to it as a stretching/compressing motion, and from now on it

will just be called a stretch.

32 Foundations

r/Å

20 000

40 000

60 000

Pb(

P) + H(

Pb(

D) + H(

Pb(

S) + H(

Pb(

+ H(

Wavenumber/cm

−1

−

∆

−

Figure 5.4 Potential energy curves for PbH obtained from sophisticated ab initio calculations. This

ﬁgure is adapted from work reported by A. B. Alekseyev and co-workers (Mol. Phys. 88 (1996) 591).

Notice that not all potential curves are Morse-like. In this ﬁgure several repulsive curves can be seen

which are unbound at all internuclear separations; an example is the 1

 state, which dissociates to

ground state atoms. In addition, some curves have double wells caused by mixing of character with

other potential energy curves of the same symmetry.

is a linear molecule. When it vibrates, both carbon–oxygen bonds will stretch and

compress, and in addition the molecule may undergo bending vibrational motion in which

the bond angle oscillates about the equilibrium angle, θ

=180

◦

.Tokeep things as simple as

possible, the bending motion will be ignored to begin with and the focus will be solely on the

bond stretches. We have seen that for diatomic molecules the vibrational potential energy

is approximately quadratic in the distortion coordinate, r − r

.Itistherefore reasonable

to suppose that the same type of potential energy relationship holds for each bond in a

polyatomic molecule. The vibrational potential energy would therefore be

V =

(5.15)

5 Molecular vibrations

where r

and r

are the displacements of the two CO bonds from their equilibrium positions

and k

is the force constant for a C O bond. This potential energy function could be

inserted into the Schr¨odinger equation (5.4), but it would be incomplete because the kinetic

energy part would also need modifying. The kinetic energy term can also be written in terms

of the displacements r

and r

, and one obtains the slightly lengthy expression

T =

+ m

)



˙r

+ ˙r



˙r

(5.16)

where M = m

+ 2m

and ˙r

are the ﬁrst derivatives of r

and r

with respect to time.

The key point to note is that the ﬁnal term on the right-hand side of (5.16)isacross-term in

the coordinates r

and r

.Ifthis cross-term was absent the vibrational Schr¨odinger equation

could be solved by the method of separating variables, which would involve transforming the

Schr¨odinger equation into two separate equations, one involving only r

and the other only

. These equations would each be equivalent to the Schr¨odinger equation for a diatomic

harmonic oscillator, and so the solutions would possess the same general form. However, the

presence of the cross-term in the kinetic energy operator (5.16) prevents such a separation,

in much the same way that the interelectronic repulsion terms in the electronic Schr¨odinger

equation prevent a separation in that case (see Section 2.1.4).

Fortunately, there is a way to remove the cross-term. This involves switching to a dif-

ferent coordinate system, the normal coordinate system. It is possible to show that for

all molecules, providing we make the assumption of simple harmonic oscillation in each

internal coordinate (a bond length or bond angle), a set of coordinates can be chosen which

give no cross-terms in either the kinetic or potential energy operators; these are the normal

coordinates for the molecule. Methods are available for working out the form of these co-

ordinates (see References [3, 4]), but here we concentrate on the results. For CO

there are

two stretching normal coordinates, designated Q

and Q

,which are as follows:



− x

)



− 2m

+ m

) (5.17)

The quantities x

, x

, and x

are the displacements of the individual atoms (1, O; 2, C; 3, O),

and M is the total mass of the molecule (= m

+ 2m

). If the kinetic and potential energy

operators are recast as functions of the two normal coordinates, no cross-terms arise and a

diatomic-like vibrational Hamiltonian is obtained for each normal coordinate Q

, i.e.

=−

2µ

∂

∂ Q

(5.18)

Solution of the Schr¨odinger equation for each normal coordinate is achieved in exactly the

same manner as for diatomics. However, it is important to recognize that the vibrational

coordinate may involve displacements of more than two atoms. We now have, therefore,

a rather simple picture of a vibrating CO

molecule. Providing we restrict it to linear

geometries, it has two normal modes of vibration, each having a vibrational term value

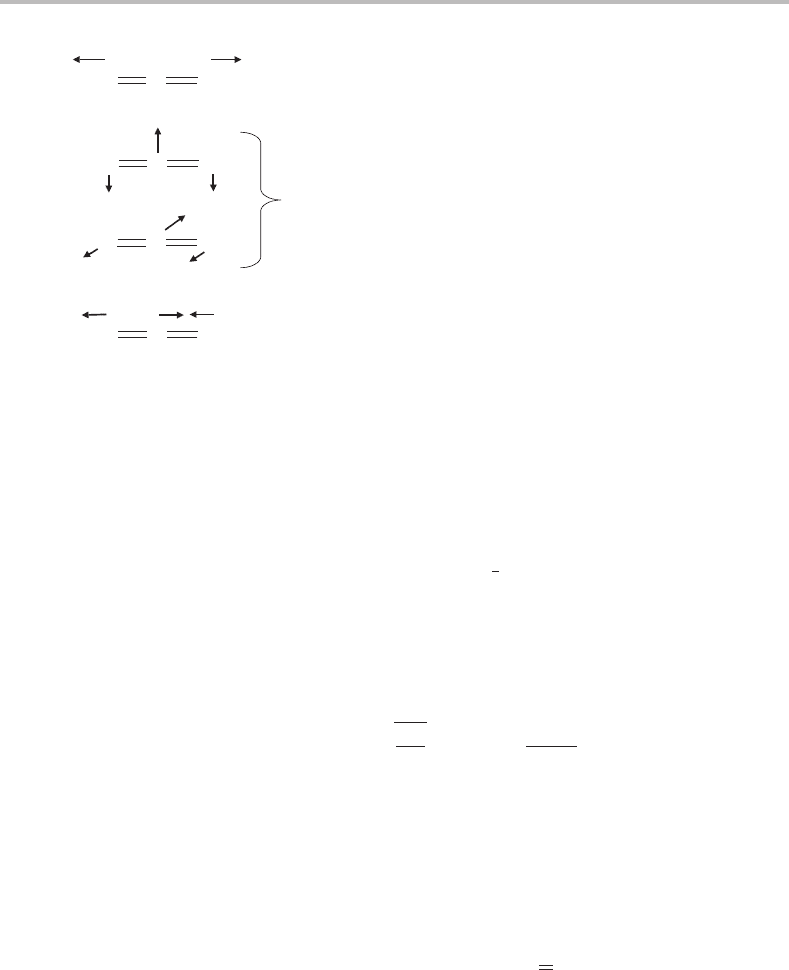
34 Foundations

Antisymmetric

C=O stretch

Symmetric C=O

stretch

Bend

)(

= 1388 cm

−1

)

= 667 cm

−1

)

= 2349 cm

−

)

Figure 5.5 Schematic illustration of the vibrational normal modes of CO

. Also included in the ﬁgure

are the symmetries and the harmonic frequencies of each mode. Lower case labels are commonly

used to show the symmetries of individual vibrations.

given by the diatomic-like harmonic oscillator expression

G(v

) = ω





(5.19)

where i identiﬁes the particular normal mode, v

is the vibrational quantum number and

is the corresponding harmonic vibrational wavenumber of this mode. Each mode has a

diatomic-like wavefunction of the form

= N



2π



cω



exp



−

cω



(5.20)

and the overall vibrational wavefunction is a product of the wavefunctions of the individual

modes. It is important to recognize that the vibrational quantum numbers for each mode are

independent quantities and so any combination of values is possible.

Let us now try to visualize what is happening for CO

in the light of the above results,

and then extend this picture to other molecules. Two independent normal vibrational modes

have been identiﬁed. One of these, designated v

and having a normal coordinate Q

involves in-phase stretching and compressing of the two C

O bonds, as can be seen from

the form of the normal coordinate in (5.17), which is also shown pictorially in Figure 5.5.

The centre-of-mass must be stationary during a vibration, otherwise the motion will be a

mixture of vibration and overall molecular translation and we are not interested in the latter.

The centre-of-mass does not move during vibration v

, since any displacement of one O

atom is exactly compensated for by motion of the other O atom in the opposite direction

(the C atom is at the centre-of-mass and it therefore does not move during this vibration).

This mode is called the symmetric stretch because it maintains the equilibrium point group

symmetry of the molecule at all stages of the vibrational motion.