Edelstein-Keshet L. Mathematical Models in Biology

Discrete Processes

in

Biology

sively

on

what

causes these geometric designs

and

patterns

in

plants, although

the

subject

has

been pursued

for

over

three centuries.

2

Fibonacci stumbled unknowingly onto

the

esoteric realm

of r

through

a

ques-

tion

growth

of

rabbits (see problem 14). Equation

(1) is

arguably

the

first

mathematical idealization

of a

biological

phenomenon phrased

in

terms

of a re-

cursion relation,

or in

more common terminology,

a

difference

equation.

Leaving aside

the

mystique

of

golden rectangles, parastichies,

and

rabbits,

we

find

that

in

more mundane realms, numerous biological events

can be

idealized

by

models

in

which similar discrete equations

are

involved. Typically, populations

for

which difference equations

are

suitable

are

those

in

which adults

die and are

totally

replaced

by

their progeny

at fixed

intervals

(i.e.,

generations

do not

overlap).

In

such

cases,

a

difference equation might summarize

the

relationship between popula-

tion density

at a

given generation

and

that

of

preceding generations. Organisms that

undergo abrupt changes

or go

through

a

sequence

of

stages

as

they

mature

(i.e.,

have discrete life-cycle stages)

are

also commonly described

by

difference

equa-

tions.

The

goals

of

this chapter

are to

demonstrate

how

equations

such

as (1)

arise

in

modeling

biological

phenomena

and to

develop

the

mathematical techniques

to

solve

the

following problem: given particular starting population levels

and a

recursion

re-

lation, predict

the

population level

after

an

arbitrary number

of

generations have

elapsed.

(It

will soon

be

evident that

for a

linear equation such

as

(1),

the

mathemat-

ical sophistication required

is

minimal.)

To

acquire

a

familiarity with difference equations,

we

will begin with

two

rather

elementary examples:

cell

division

and

insect growth.

A

somewhat more elab-

orate problem

we

then investigate

is the

propagation

of

annual

plants. This topic will

furnish

the

opportunity

to

discuss

how a

slightly more complex model

is

derived.

Sections

1.3 and 1.4

will

outline

the

method

of

solving certain linear

difference

equations.

As a

corollary,

the

solution

of

equation

(1) and its

connection

to the

golden

mean will

emerge.

1.1

BIOLOGICAL

MODELS

USING

DIFFERENCE

EQUATIONS

Cell

Division

Suppose

a

population

of

cells

divides synchronously,

with

each member producing

a

daughter

cells.

3

Let us

define

the

number

of

cells

in

each generation with

a

subscript,

that

is, M1, M

2

, . . . , M

n

are

respectively

the

number

of

cells

in the first,

second,

. . . , nth

generations.

A

simple equation relating successive generations

is

2. An

excellent

summary

of the

phenomena

of

phyllotaxis

and the

numerous

theories

that

have

arisen

to

explain

the

observed

patterns

is

given

by R. V.

Jean

(1984).

His

book contains

nu-

merous suggestions

for

independent

research

activities

and

problems related

to

phyllotaxis.

See

also

Thompson (1942).

3.

Note that

for

real

populations only

a > 0

would make

sense;

a < 0 is

unrealistic,

and

a

= 0

would

be

uninteresting.

6

The

Theory

of

Linear

Difference

Equations

Applied

to

Population

Growth

1

Let us

suppose

that initially there

are Mo

cells.

How big

will

the

population

be

after

n

generations?

Applying equation

(2)

recursively results

in the

following:

Thus,

for the nth

generation

We

have arrived

at a

result worth remembering:

The

solution

of a

simple linear dif-

ference

equation involves

an

expression

of the

form

(some number)", where

n is the

generation number. (This

is

true

in

general

for

linear difference equations.) Note that

the

magnitude

of a

will determine whether

the

population grows

or

dwindles

with

time.

That

is,

a

> 1 M

n

increases over successive generations,

< 1 M

n

decreases over successive generations,

a

= 1 M

n

is

constant.

An

Insect Population

Insects generally have more than

one

stage

in

their

life

cycle

from

progeny

to

matu-

rity. The

complete

cycle

may

take weeks, months,

or

even years. However,

it is

cus-

tomary

to use a

single

generation

as the

basic unit

of

time when attempting

to

write

a

model

for

insect population growth. Several stages

in the

life

cycle

can be

depicted

by

writing several difference equations.

Often

the

system

of

equations condenses

to

a

single

equation

in

which combinations

of all the

basic

parameters appear.

As

an

example

consider

the

reproduction

of the

poplar gall aphid. Adult female

aphids produce galls

on the

leaves

of

poplars.

All the

progeny

of a

single aphid

are

contained

in one

gall (Whitham, 1980). Some

fraction

of

these will emerge

and

sur-

vive

to

adulthood. Although generally

the

capacity

for

producing

offspring

(fecundity)

and the

likelihood

of

surviving

to

adulthood (survivorship) depends

on

their environmental conditions,

on the

quality

of

their

food,

and on the

population

sizes,

let us

momentarily ignore these

effects

and

study

a

naive model

in

which

all

parameters

are

constant.

First

we

define

the

following:

a

n

=

number

of

adult female aphids

in the nth

generation,

p

n

=

number

of

progeny

in the nth

generation,

m =

fractional mortality

of the

young

aphids,

/ =

number

of

progeny

per

female aphid,

r =

ratio

of

female aphids

to

total adult aphids.

Then

we

write equations

to

represent

the

successive

populations

of

aphids

and

use

these

to

obtain

an

expression

for the

number

of

adult females

in the nth

genera-

tion

if

initially there were

a

0

females:

8

Discrete Processes

in

Biology

Equation

(7) is

again

a first-order

linear difference equation,

so

that solution

(8)

fol-

lows

from

previous remarks.

The

expression

fr(1

– m) is the per

capita number

of

adult

females that each mother aphid produces.

1.2

PROPAGATION

OF

ANNUAL PLANTS

Annual

plants produce seeds

at the end of a

summer.

The flowering

plants wilt

and

die, leaving their progeny

in the

dormant

form

of

seeds that must survive

a

winter

to

give rise

to a new

generation.

The

following spring

a

certain fraction

of

these seeds

germinate. Some seeds might remain dormant

for a

year

or

more before reviving.

Others

might

be

lost

due to

predation, disease,

or

weather.

But in

order

for the

plants

to

survive

as a

species,

a

sufficiently

large population must

be

renewed

from

year

to

year.

In

this section

we

formulate

a

model

to

describe

the

propagation

of

annual

plants.

Complicating

the

problem somewhat

is the

fact

that annual plants produce

seeds that

may

stay dormant

for

several years before germinating.

The

problem thus

requires

that

we

systematically

keep

track

of

both

the

plant population

and the re-

serves

of

seeds

of

various ages

in the

seed bank.

Stage

1:

Statement

of the

Problem

Plants produce seeds

at the end of

their growth season (say August),

after

which they

die.

A

fraction

of

these

seeds

survive

the

winter,

and

some

of

these germinate

at the

beginning

of the

season (say May), giving

rise to the new

generation

of

plants.

The

fraction

that germinates depends

on the age of the

seeds.

Each female produces

f

progeny; thus

Of

these,

the fraction 1 — m

survives

to

adulthood, yielding

a final

proportion

of r

females.

Thus

While equations

(5) and (6)

describe

the

aphid population, note that these

can be

combined into

the

single statement

For the

rather

theoretical

case

where

f, r, and m are

constant,

the

solution

is

where

a

0

is the

initial number

of

adult females.

The

Theory

of

Linear

Difference

Equations

Applied

to

Population

Growth

9

Stage

2:

Definitions

and

Assumptions

We first

collect

all the

parameters

and

constants specified

in the

problem. Next

we

define

the

variables.

At

that

stage

it

will prove

useful

to

consult

a

rough sketch such

as

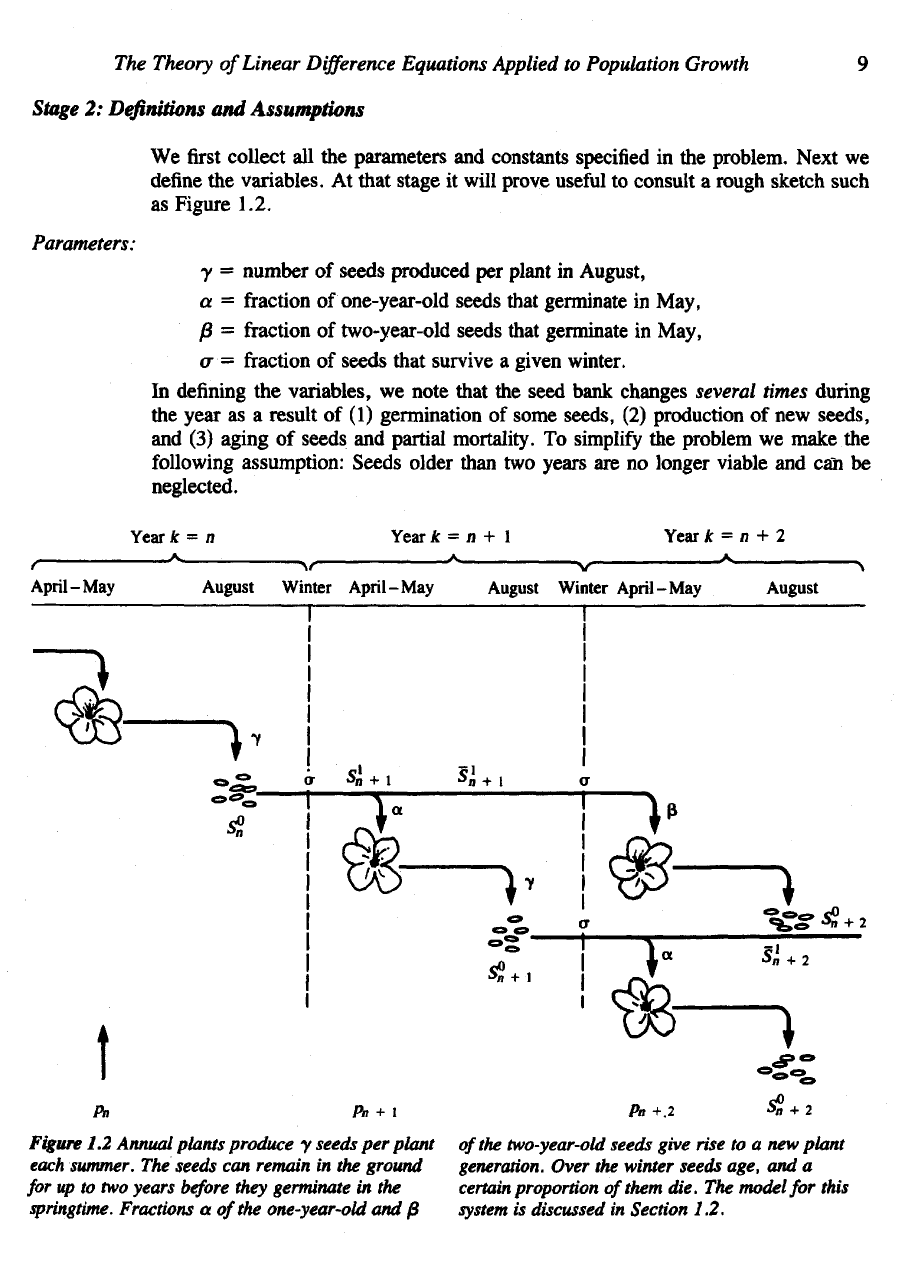
Figure 1.2.

Parameters:

r =

number

of

seeds

produced

per

plant

in

August,

a =

fraction

of

one-year-old

seeds that germinate

in

May,

ß = fraction of

two-year-old seeds that germinate

in

May,

a =

fraction

of

seeds that survive

a

given winter.

In

defining

the

variables,

we

note that

the

seed bank changes

several

times

during

the

year

as a

result

of (1)

germination

of

some seeds,

(2)

production

of new

seeds,

and

(3)

aging

of

seeds

and

partial mortality.

To

simplify

the

problem

we

make

the

following assumption:

Seeds

older

than

two

years

are no

longer viable

and can be

neglected.

Figure

1.2

Annual plants produce

y

seeds

per

plant

each

summer.

The

seeds

can

remain

in the

ground

for

up to two

years

before

they germinate

in the

springtime.

Fractions

a

of

the

one-year-old

and ß

of

the

two-year-old seeds give rise

to a new

plant

generation. Over

the

winter seeds

age,

and a

certain

proportion

of

them

die.

The

model

for

this

system

is

discussed

in

Section

1.2.

10

Discrete Processes

in

Biology

Consulting Figure 1.2,

let us

keep track

of the

various quantities

by

defining

p

n

=

number

of

plants

in

generation

n,

Sn

=

number

of

one-year-old seeds

in

April (before germination),

S2n

=

number

of

two-year-old seeds

in

April (before germination),

S1n =

number

of

one-year-old seeds

left

in May

(after

some have germinated),

S2n

=

number

of

two-year-old seeds

left

in May

(after

some have germinated),

S0n =

number

of new

seeds produced

in

August.

Later

we

will

be

able

to

eliminate some

of

these variables.

In

this

first

attempt

at

for-

mulating

the

equations

it

helps

to

keep track

of all

these quantities. Notice that

su-

perscripts refer

to age of

seeds

and

subscripts

to the

year number.

Stage

3: The

Equations

In

May,

a

fraction

a of

one-year-old

and ß of

two-year-old seeds produce

the

plants.

Thus

The

seed

bank

is

reduced

as a

result

of

this germination.

Indeed,

for

each

age

class,

we

have

Thus

In

August,

new

(0-year-old) seeds

are

produced

at the

rate

of y per

plant:

Over

the

winter

the

seed

bank changes

by

mortality

and

aging.

Seeds

that were

ne

in

generation

n

will

be one

year

old in the

next generation,

n + 1.

Thus

we

have

Stage

4:

Condensing

the

Equations

We

now use

information

from

equations (9a–f)

to

recover

a set of two

equations

linking

successive plant

and

seed

generations.

To do so we

observe that

by

using

equation (9d)

we can

simplify (9e)

to the

following:

The

Theory

of

Linear

Difference

Equations

Applied

to

Population

Growth

11

Sim rly,

from

equation (9b) equation (9f) becomes

Now

let us

rewrite equation (9a)

for

generation

n + 1 and

make some substitutions:

Using

(10), (11),

and

(12)

we

arrive

at a

system

of two

equations

in

which plants

and

one-year-old seeds

are

coupled:

Notice that

it is

also

possible

to

eliminate

the

seed

variable altogether

by first

rewrit-

ing

equation (13b)

as

and

then substituting

it

into equation (13a)

to get

We

observe that

the

model

can be

formulated

in a

number

of

alternative ways,

as

a

system

of two

first-order equations

or as one

second-order equation (15). Equa-

tion

(15)

is

linear since

no

multiples

p

n

p

m

or

terms that

are

nonlinear

in p

n

occur;

it is

second order since

two

previous generations

are

implicated

in

determining

the

present generation.

Notice that

the

system

of

equations (13a

and b)

could also have been written

as

a

single equation

for

seeds.

Stage

5:

Check

To be on the

safe

side,

we

shall

further

explore equation (15)

by

interpreting

one of

the

terms

on its right

hand side. Rewriting

it for the nth

generation

and

reading

from

right to

left

we see

that

p

n

is

given

by

The first

term

is

more elementary

and is

left

as an

exercise

for the

reader

to

translate.

12

Discrete Processes

in

Biology

1.3

SYSTEMS

OF

LINEAR DIFFERENCE EQUATIONS

The

problem

of

annual plant reproduction leads

to a

system

of two first-order

differ-

ence equations (10,13),

or

equivalently

a

single second-order equation (15).

To un-

derstand

such equations,

let us

momentarily turn

our

attention

to a

general

system

of

the

form

As

before, this

can be

converted

to a

single higher-order equation. Starting

with

(16a)

and

using (16b)

to

eliminate y

n+1

,

we

have

From equation (16a),

Now

eliminating

y

n

we

conclude that

or

more simply that

In

a

later chapter, readers

may

remark

on the

similarity

to

situations encountered

in

reducing

a

system

of

ordinary

differential

equations (ODEs)

to

single ODEs (see

Chapter

4). We

proceed

to

discover properties

of

solutions

to

equation (17)

or

equiv-

alently,

to

(16a,

b).

Looking

back

at the

simple

first-order

linear difference equation (2),

recall

that

solutions

to it

were

of the

form

While

the

notation

has

been changed slightly,

the

form

is

still

the

same: constant

de-

pending

on

initial conditions times some number raised

to the

power

n.

Could this

type

of

solution work

for

higher-order linear equations such

as

(17)?

We

proceed

to

test this idea

by

substituting

the

expression

x

n

=

Chn"

(in the

form

of

x

n+1

=

Ch

n+1

and

x

n+2

=

CA

n+2

)

into equation (17), with

the

result that

Now

we

cancel

out a

common factor

of

CA".

(It may be

assumed that

CA" = 0

since

x

n

= 0 is a

trivial solution.)

We

obtain

Thus

a

solution

of the

form (18) would

in

fact

work, provided that

A

satisfies

the

quadratic equation (19), which

is

generally called

the

characteristic equation

of

(17).

The

Theory

of

Linear

Difference

Equations

Applied

to

Population Growth

13

To

simplify notation

we

label

the

coefficients appearing

in

equation (19)

as

follows:

The

solutions

to the

characteristic

equation (there

are two of

them)

are

then:

These numbers

are

called eigenvalues,

and

their properties will uniquely determine

the

behavior

of

solutions

to

equation (17).

(Note:

much

of the

terminology

in

this

section

is

common

to

linear algebra;

in the

next section

we

will arrive

at

identical

re-

sults

using matrix notation.)

Equation (17)

is

linear; like

all

examples

in

this chapter

it

contains only scalar

multiples

of the

variables—no quadratic, exponential,

or

other nonlinear expres-

sions.

For

such equations,

the

principle

of

linear

superposition

holds:

if

several

dif-

ferent

solutions

are

known, then

any

linear combination

of

these

is

again

a

solution.

Since

we

have just determined that

A" and A3 are two

solutions

to

(17),

we can

con-

clude that a general solution is

provided

h1 = h

2

.

(See problem

3 for a

discussion

of the

case

h1 =

h

2

.) This

ex-

pression

involves

two

arbitrary

scalars,

A1 and A

2

,

whose values

are not

specified

by

the

difference equation (17) itself. They depend

on

separate constraints, such

as

par-

ticular known values attained

by x.

Note that specifying

any two x

values uniquely

determines

A1 and A

2

.

Most commonly,

xo and x1, the

levels

of a

population

in the

first two

successive generations,

are

given

(initial

conditions)',

A1 and A

2

are

deter-

mined

by

solving

the two

resulting linear algebraic equations (for

an

example

see

Section 1.7).

Had we

eliminated

x

instead

of y

from

the

system

of

equations (16),

we

would have obtained

a

Edelstein-Keshet L. Mathematical Models in Biology

Подождите немного. Документ загружается.