Edelstein-Keshet L. Mathematical Models in Biology
Подождите немного. Документ загружается.


xl
Mathematical
Models
in
Biology
•
Page 422, Problem 18(b):
See
Section 8.1.
•
Page 424, Problem
22:
Page 425: Both bibliography items under Hardt should have
the
name
"Hardt,
S. L."
Chapter
10.
•
Page 444, line
2:
"where
K =
k/(m
+
1)."
•
Page 452, line
-5: "a
population
of
individuals carrying
a
slightly advan-
tageous recessive allele"...
•
Page 454:
The top figure is
incorrect. Disregard.
•
Page 464, line
before
Figure 10.8: "per unit time uj."
•
Page 477, Problem 2(a):
The
right-hand side
of the
equation should read
-V(fv)–uf.."
•
Page 479, Problem 6(b):
Co = 7 x
10
7
.
•
Page 480, Problem
7:
Note
that
if
step
length
Ax is
constant, then
in 3 di-
mensions,
u =
(Ax2/6r
.
Lovely
and
Dahlquist (1975) consider
a
more general
problem,
where
the
step
length
is
Poisson distributed
to get u =
(l/3)v\.
•
Page 487: Delete problem
21
(b).
•
Page 481, Problem 8(e):
A
better scaling suggested
is:
•
Page 493:
The
Takahashi
references
are
identical. Replace
the
second
one
with
Takahashi,
M.
(1968) Theoretical basis
for
cell cycle analysis
II.
Further
studies
on
labeled mitosis
wave
method,
J.
Theor.
Biol.,
18,
195-209.

Errata
xli
Chapter
11.
•
Page 502: Equation (2b) should have
the
corrected term
Then equation (45)
can be
replaced
by the
condition
for
instability:
•
Page 516, bottom
of
page:
The
heading Positive
feedback
is
better described
as
Substrate
depletion.
•
Page 517:
After
equation (43)
it
should read "... otherwise
the
inequality
a11
+ a22 > 0
contradicts (32a)."
In
equations
(44a,b)
the
tau's
would
be
better defined
as
time constants:
Page 513: Equation (37) should have
the
corrected term:
•
Page 506, bottom third
of
page: Second condition should read
"2.
Values
of
L
must
not be too
small."
•
Page 507,
top
part
of
page: replace
first two
comments
as
follows:
1.
Aggregation
is
favored
more highly
in
larger domains
than
in
smaller
ones
at fixed a.
2.
The
perturbations most likely
to be
unsta
re
those with
low
wavenumbers....
The
perturbation whose wavenumber
is q =
r/L.
..
Comment
(due
to
John Tyson):
Let Xaf be the
bifurcation parameter.
For
Xaf
< uk, the
homogeneous solution
is
stable with respect
to
perturba-
tions
of all
wavenumbers
q. As Xaf
increases above
uk,
the
homogeneous
solution becomes unstable with respect
to
long wavelength perturbations.
The first
possible pattern
is
11.3(a),
and
this arises when
xaf >
uk+uDr2/L2"
.
As
Xaf
increases
further,
other
patterns
become possible.

xlii
Mathematical
Models
in
Biology
where
L1 =
DIT\
is the
range
of the
activator
and L2 =
D2T2
is the
range
of
the
inhibitor.
•
Page 519: Comment about equation (46)
by
John Tyson:
The
term
in
round braces
is
then
the
harmonic mean
of the
ranges
of ac-
tivation
and
inhibition. Further,
d ~ qL1
since
L1 «
L2.
•
Page
521: Comment about qi,q2
by
John Tyson:
We
expect
that
q1 ~ q2,
so
that
Q
2
~
2q
2
.
Amplified
waves
are
then those with
Page 522,
top of
page:
D/a ~
area
of
range
of
activator,
L2a/D~
ratio
of
area characterizing domain
to
range
of
activation,
a/ß =
ratio
of
range
of
activation
to
range
of
inhibition.
•
Page 531:
The
left-hand side
of
equation
62
(a)
should read u,Dh–vD
a
> ...
•
Page 545, Problem
3: the
inequality
is
incorrect. Disregard'.
•
Page 548, Problem 15(g):
Selected Answers.
•
Page 556, Chapter
1,
Problem
3:
Mislabeling should
be
corrected
as
fol-
lows:
(i)
->
(ii); (ii)
->
(iii); (iii)
-»
(iv).
Chapter
1,
Problem
9(c):
Argument
of
trig
functions
should
be
^.
•
Page 557, Chapter
2,
Problem
l(a):
x
n
= C

Errata
xliii
•
Page 558, Chapter
3,
4(c):
stable
for
|1 +b
(h–
1/b
1)| < 1.
•
Page 5 (e): Rightmost arrow should point right instead
of
left.
•
Page 562: Problems mislabled:
20
—>
21; 21
—>
22
•
Page 568: 8(b)
is
i t. Disregard.
•
Page 569, 8(e): Replace
K
with
K.
I
would like
to
thank
those
people
who
submitted
errata.
Special thanks
to
John Tyson
for
many
helpful
comments
and for the
extended loan
of his
personal
annotated copy.
This page intentionally left blank

I
Discrete Processes
in
Biology
This page intentionally left blank

1 The
Theory
of
Linear
Difference
Equations
Applied
to
Population
Growth
For we
will
always
have
as 5 is to 8 so is 8 to 13,
practically,
and as 8 is to
13, so is 13 to 21
almost.
I
think
that
the
seminal
faculty
is
developed
in a
way
analogous
to
this proportion which
perpetuates
itself,
and so in the
flower is
displayed
a
pentagonal
standard,
so to
speak.
I let
pass
all
other
considerations
which
might
be
adduced
by the
most
delightful
study
to
establish
this truth.
J.
Kepler, (1611). Sterna
seu de
nive sexangule,
Opera,
ed.
Christian
Frisch, tome
7,
(Frankefurt
a
Main, Germany: Heyden
&
Zimmer,
1858-1871),
pp.
722-723.
The
early Greeks were fascinated
by
numbers
and
believed them
to
hold
special
magical properties. From
the
Greeks'
special blend
of
philosophy, mathematics,
nu-
merology,
and
mysticism, there emerged
a
foundation
for the
real number system
upon
which modern mathematics
has
been built.
A
preoccupation with aesthetic
beauty
in the
Greek civilization meant, among other things, that architects, artisans,
and
craftsmen based many
of
their works
of art on
geometric principles.
So it is
that
in
the
stark ruins
of the
Parthenon many regularly spaced columns
and
structures
capture
the
essence
of the
golden mean, which derives
from
the
golden rectangle.
Considered
to
have
a
most visually pleasing proportion,
the
golden rectangle
has
sides
that bear
the
ratio
r =
1:1.618033.
. . . The
problem
of
subdividing
a
line
segment into this
so-called
extreme
and
mean ratio
was a
classical problem
in
Greek
geometry, appearing
in the
Elements
of
Euclid (circa
300
B.C.).
It was
recognized
then
and
later that this divine proportion,
as Fra
Luca
Pacioli
(1509)
called
it, ap-
pears
in
numerous
geometric
figures, among them
the
pentagon,
and the
polyhedral
icosahedron
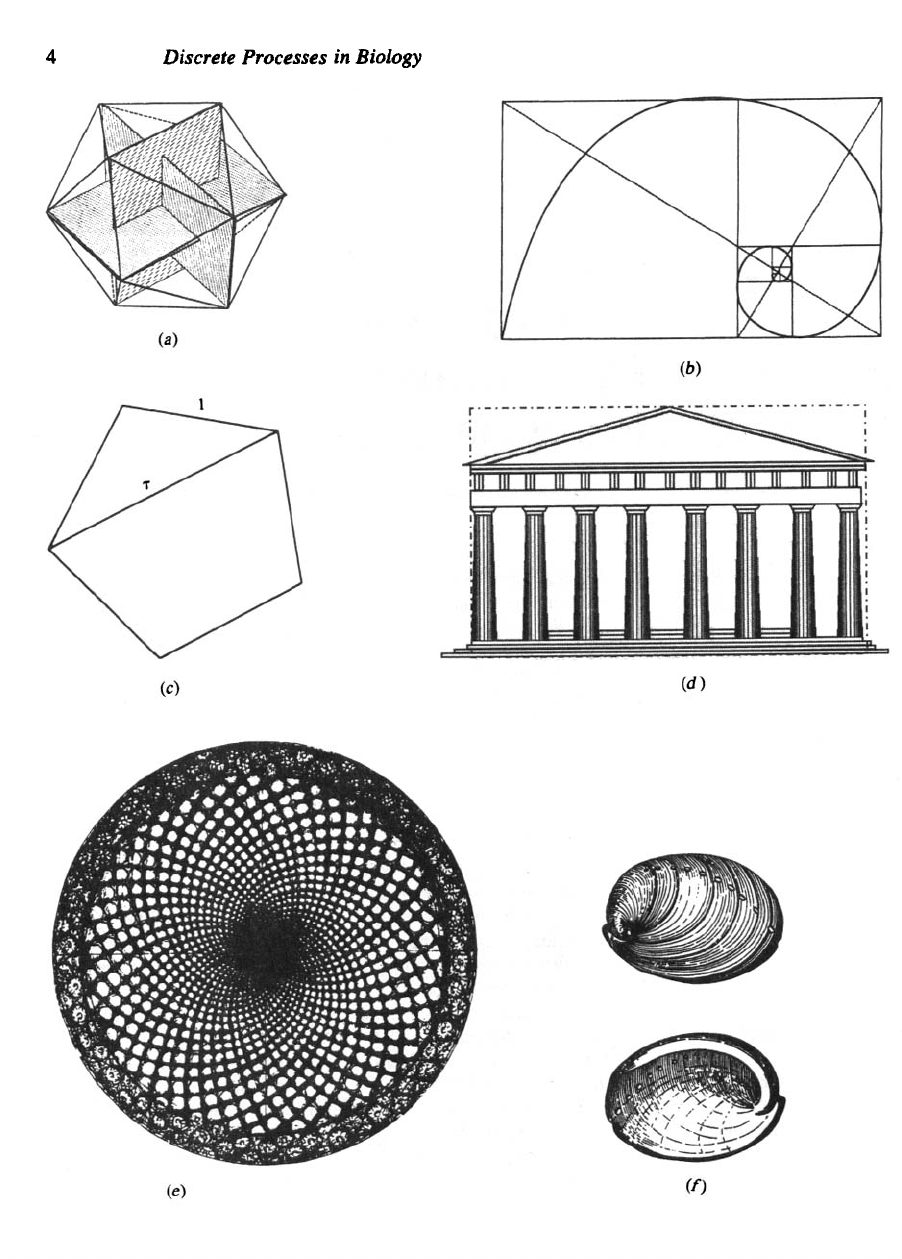
(see
Figure
1.1).
Discrete
Processes
in
Biology
4

The
Theory
of
Linear
Difference
Equations
Applied
to
Population
Growth
5
About
fifteen
hundred years
after
Euclid, Leonardo
of
Pisa
(1175–1250),
an
Italian mathematician more affectionately known
as
Fibonacci ("son
of
good
na-
ture")
,
proposed
a
problem whose solution
was a
series
of
numbers that eventually
led to a
reincarnation
of T. It is
believed that Kepler (1571–1630)
was the first to
recognize
and
state
the
connection between
the
Fibonacci
numbers
(0, 1, 1, 2, 3, 5,
8, 13, 21, .. .), the
golden mean,
and
certain aspects
of
plant growth.
Kepler observed that successive elements
of the
Fibonacci sequence
satisfy
the
following
recursion relation
Figure
1.1 The
golden mean
r
appears
in a
variety
of
geometric forms that include:
(a)
Polyhedra such
as
the
icosahedron,
a
Platonic solid with
20
equilateral
triangle faces
(r =
ratio
of
sides
of
an
inscribed
golden rectangle; three golden rectangles
are
shown here),
(b) The
golden rectangle
and
every
rectangle formed
by
removing
a
square from
it.
Note that corners
of
successive squares
can be
connected
by a
logarithmic spiral),
(c) A
regular
pentagon
(r = the
ratio
of
lengths
of
the
diagonal
and a
side),
(d) The
approximate proportions
of
the
Parthenon
(dotted
line indicates
a
golden
rectangle),
(e)
Geometric designs such
as
spirals
that
result
from the
arrangement
of
leaves, scales,
or
florets on
plants (shown here
on the
head
of
a
sunflower).
The
number
of
spirals running
in
opposite
directions quite
often
bears
one
of
the
numerical
ratios
2/3, 3/5, 5/8, 8/13, 13/21,
21/34,
34/5,
. . .
[see
R. V.
Jean (1984, 86)];
i.e., each member equals
the sum of its two
immediate predecessors.
1
He
also noted
that
the
ratios 2:1, 3:2, 5:3, 8:5, 13:8,
. . .
approach
the
value
of r.
2
Since then,
manifestations
of the
golden mean
and the
Fibonacci numbers have appeared
in
art,
architecture,
and
biological
form.
The
logarithmic
spirals
evident
in the
shells
of
certain mollusks
(e.g.,
abalone,
of the
family
Haliotidae)
are
figures
that result
from
growth
in
size without change
in
proportion
and
bear
a
relation
to
successively
in-
scribed golden rectangles.
The
regular arrangement
of
leaves
or
plant parts along
the
stem, apex,
or flower of a
plant, known
as
phyllotaxis, captures
the
Fibonacci num-
bers
in a
succession
of
helices (called
parastichies);
a
striking example
is the ar-
rangement
of
seeds
on a ripening
sunflower.
Biologists have
not yet
agreed conclu-
1.
The
values
n0 and n1 are
defined
to be 0 and 1.
2.
Certain aspects
of the
formulation
and
analysis
of the
recursion relation
(1)
governing
Fibonacci
numbers
are
credited
to the
French mathematician Albert Girard,
who
developed
the al-
gebraic notation
in
1634,
and to
Robert Simson (1753)
of the
University
of
Glasgow,
who
recog-
nized ratios
of
successive members
of the
sequence
as r and as
continued
fractions
(see prob-
lem
12).
note that
these
are the
ratios
of
successive
Fibonacci
numbers,
(f)
Logarithmic
spirals
(such
as
those
obtained
in (b) are
common
in
shells such
as
the
abalone
Haliotis,
where each increment
in
size
is
similar
to the
preceding one.
See D. W.
Thompson
(1974)
for an
excellent
summary,
[(a and
b)
from M.
Gardner
(1961),
The
Second Scientific
American
Book
of
Mathematical Puzzles
and
Diversions,
pp.
92–93.
Copyright
1961
by
Martin
Gardner.
Reprinted
by
permission
of
Simon
&
Schuster,
Inc., N.Y., N.Y.
(d)from
G.
Gromort
(1947),
Histoire abregee
de
l'Architecture
en
Grece
et
a
Rome,
Fig 43 on p. 75,
Vincent
Freal
&
Cie,
Paris,
France,
(e)from
S.
Colman (1971), Nature's
Harmonic
Unity, plate
64, p. 91;
Benjamin
Blom,
N.Y. (reprinted
from the
1912 edition),
(f) D.
Thompson
(1961),
On
Growth
and
Form
(abridged
ed.)
figure 84, p.
186.
Reprinted
by
permission
of
Cambridge University
Press,
New
York.]
