Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Подождите немного. Документ загружается.

что дрифт не имеет никакого физического смысла. Доверительный интервал просто указывает

ошибку опробования и дает наиболее вероятное значение для дрифта регионализованной перемен-

ной в случае, если бы она подвергалась повторно опробованию, и дрифт вычислялся бы повторно.)

Для того, чтобы численные примеры этого параграфа оказались доступными, было сделано

много упрощений.

Например, используемое число наблюдений является наименьшим из возможных. В дейст-

вительных приложениях рассматривается значительно большее число контрольных точек, так как

это увеличивает точность крайгинга и уменьшает ошибку оценки. Аналогично, предполагается ли-

нейность полувариограммы, так как это простейшая из возможных моделей, имеющая только один

параметр. Строго линейная полувариограмма не имеет максимума, а может быть продолжена до

бесконечных значений дисперсии. В действительности же мы имеем линейную полувариограмму

вплоть до некоторого значения, и только после излома она становится постоянной. Армстронг и

Жабин [3] указали, что полувариограммы, обладающие внезапными изменениями наклона, могут

приводить к неустойчивым решениям и отрицательным дисперсиям. Для представления полуварио-

граммы оказывается удобнее использовать непрерывную функцию, такую, как, например, сфериче-

ская модель, хотя это несколько усложняет вычисления. Неизвестно, не является ли слишком жест-

ким требование линейности полувариограммы, но так как оно довольно широко используется на

практике, то, очевидно, им можно пренебречь. Неопределенность в правильном определении апри-

орной оценки дисперсии остатков также не слишком обременительна, так как только оценка ошибки

дрифта зависит от этого параметра. Сам дрифт будет вычислен правильно, независимо от выбранно-

го в качестве S

значения.

Пример

Вы уже могли заметить, что крайгинг, даже в очень упрощенном варианте, который мы рас-

смотрели, требует выполнения множества скучных арифметических действий. Практическое при-

менение крайгинга к настоящим задачам оказывается возможным лишь при использовании ЭВМ,

так как для того чтобы охарактеризовать изменения регионализованной переменной на некоторой

площади, оценки должны производиться многократно для различных точек. В качестве примера

рассмотрим карту, изображенную на рис. 5.67 и представляющую собой модификацию соответст-

вующей карты [62]. На ней представлены значения уровня воды в Экус Бедз, водоносного горизонта

на юге Центрального Канзаса. Структурный анализ, выполненный на значительно большей площа-

ди, показывает, что значения уровня воды могут рассматриваться как нестационарная регионализо-

ванная переменная, имеющая дрифт первого порядка. Область изменения полувариограммы остат-

ков от дрифта есть 28 миль. В качестве модели полувариограммы можно выбрать линейную функ-

цию с наклоном 60 квадратных футов на 1 милю.

Для построения карты уровней воды с помощью универсального крайгинга была использо-

вана программа построения карты в изолиниях, с помощью которой получались оценки уровней во-

ды в точках, расположенных на равных интервалах вдоль картируемой площади. На карте рис. 5.67

представлено 3161=1891 оценок крайгинга, каждая из которых основана на восьми ближайших

контрольных скважинах, выбранных в октанте поиска вокруг оцениваемой точки. Каждая оценка в

свою очередь требует решения системы одиннадцати уравнений.

В дополнение к карте уровней воды крайгинг был также использован для построения карты

стандартной ошибки оценок, представленной на рис. 5.68. Стандартная ошибка в каждой из 47 на-

блюдательных скважин равна нулю, но увеличивается с расстоянием от известных контрольных то-

чек (рис. 5.68). С вероятностью 95% истинная поверхность уровня воды лежит внутри интервала,

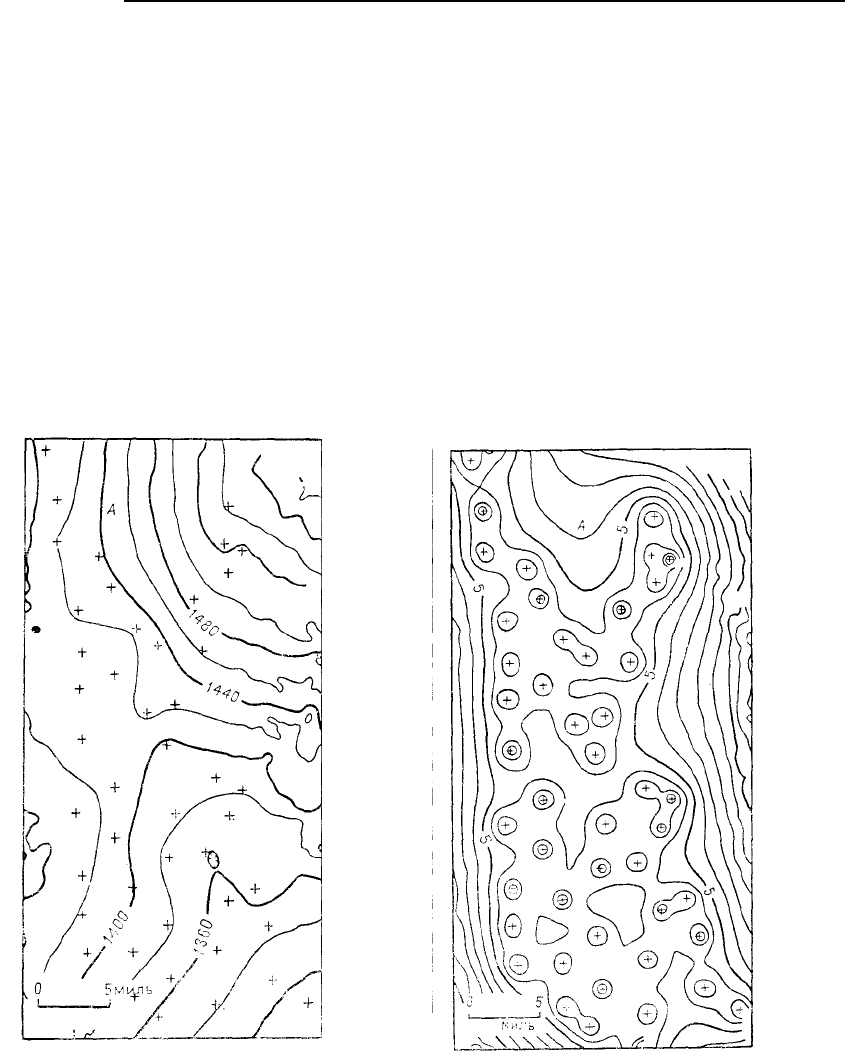
определенного с точностью плюс или минус два указанных значения. Например, в точке А уровень

воды оценивается примерно в 1480 футов. Так как имеется относительно немного наблюдательных

скважин вблизи от этой точки, то карта стандартной ошибки указывает некоторое значение более 6

футов. Поэтому истинное значение в этой точке должно быть 1480±12 футов, т. е. между 1468 и

1492 футами с доверительной вероятностью 95%.

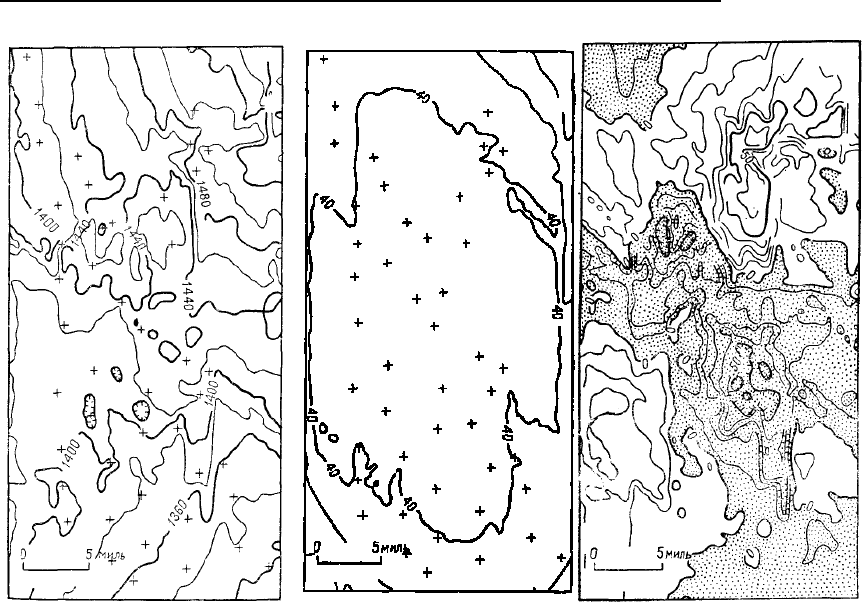
В этом примере мало геологического смысла в отношении самого дрифта, но при необходи-

мости его можно изобразить на карте. На рис. 5.69 показан дрифт первого порядка уровней воды. На

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

рис. 5.70 представлена стандартная ошибка дрифта. Остатки от дрифта, найденные вычитанием кар-

ты дрифта из карты крайгинга, представлены на рис. 5.71. Площади отрицательных остатков, где

уровни воды ниже, чем дрифт, указаны штриховкой.

Оценка значения переменной в точке по точечным наблюдениям – это лишь одно из приме-

нений крайгинга. Этот метод можно обобщить для построения оценок значений площади по выбор-

кам, состоящим из площадей или же для построения оценок значений по выборкам, соответствую-

щих объемам. Последнее применение особенно важно в горном деле, где оцениваемые величины

являются содержанием руды в блоке и наблюдения представляют собой таблицы содержаний в кер-

не скважины. Процедура оценки по существу такая же, как было описано выше, однако здесь возни-

кают дополнительные сложности из-за изменчивости в пределах площадей или объемов. Отличное

введение в использование крайгинга для оценки руды приводится в работе И. Кларк [13]. Более

подробное изложение, включающее более трудные разделы госстатистики, можно найти в книгах

Давида [21] и Журнеля и Юбре [41].

Рис. 5.67. Карта уровней воды в Экус

Бедз, большом водоносном слое в юж-

ной части Центрального Канзаса. Кар-

та построена методом универсального

крайгинга в предположении дрифта пер-

вого порядка. Уровни изолинии указаны

в футах выше уровня моря. Крестик –

наблюдательные скважины

Рис. 5.68. На карте представлена ста

н-

дартная ошибка оценок уровней воды

в Экус Бедз. Интервал между изолиния-

ми 1 фут

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Рис. 5.69. Карта, предста

в-

ляющая дрифт первого по-

рядка уровня воды в Экус

Бедз. Уровни изолиний указа-

ны в футах выше уровня моря

Рис. 5.70. Карта представл

я-

ет стандартную ошибку

дрифта первого порядка

уровней воды в Экус Бедз.

Интервал между изолиниями

равен 10 футам

Рис. 5.71. Карта, на которой

представлены остатки от

дрифта первого порядка

уровня воды в Экус Бедз. Ин-

тервал между изолиниями 10

футов. Заштрихованы площади

отрицательных остатков, на

которых уровни воды ниже

дрифта

ПОВЕРХНОСТИ ТРЕНДА

Тренд-анализ – это чисто геологическое название математического метода разделения двух

компонент: систематической и случайной по эмпирическим данным. Это разделение всегда прово-

дилось геологами интуитивно или с помощью некоторых графических построений. Так, например,

геологи-нефтяники обычно противопоставляют понятия «региональный прогиб», или «конфигура-

ция бассейна», термину «локальная структура». Петрографы могут, например, говорить о «регио-

нальной зернистости» некоторой области метаморфизма. Геофизики же привыкли к понятиям «ре-

гиональный тренд» и «локальные аномалии». Все эти выражения характеризуют ситуацию, ко гда

наблюдаемый результат является следствием двух взаимодействующих геологических факторов или

групп факторов, один (одна) из которых отражает региональную, или общую, геологическую обста-

новку, а второй (вторая) – мелкие локальные отклонения от региональных закономерностей. Весьма

наглядные примеры для иллюстрации этих соотношений можно заимствовать из структурной геоло-

гии. Так, третичный бассейн Вайоминга сформировался в результате движений земной коры по раз-

ломам глубокого заложения, тогда как складчатые структуры внутри бассейна возникли под дейст-

вием гравитационного скольжения, мелких дизъюнктивных нарушений и т.п. В подобной ситуации

форма бассейна характеризует региональную структуру, а более мелкие структуры можно рассмат-

ривать как локальные отклонения.

Понятия «региональный» и «локальный» весьма субъективны. Они в значительной степени

зависят и от размеров изучаемого региона. Так, если мы будем рассматривать всю поверхность до-

кембрия в США, то по отношению к ней бассейны и разделяющие их горные хребты Вайоминга бу-

дут локальными отклонениями, или аномалиями, как и Блэл-Хилс, купол Озарк, Мичиганский бас-

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

сейн и др. Внутри же одного бассейна Вакоминг понятия «региональный» и «локальный» имеют

совершенно иной смысл.

Имеющиеся данные также оказывают влияние на характер устанавливаемого регионального

тренда и локальных отклонений. Так, например, бесполезно искать какой-либо смысл локальных

закономерностей, если области их проявления близки по размерам и участкам опробования. Такие

закономерности независимо от того, существуют они или нет, в подобных условиях просто нельзя

установить. Меру зависимости между размерами участков проявления устанавливаемой закономер-

ности и пространственным размещением точек равномерной сети можно вычислить для правильной

сети точек [71], но не для случая нерегулярно расположенных точек, который значительно хуже

поддается математической обработке.

Цель геологического исследования также влияет на рассматриваемые нами два понятия про-

странственных соотношений. Так, например, для золоторудного месторождения в Южной Африке

представляют интерес только те «отклонения» содержаний золота, которые превышают заданное

значение, заранее определенное экономистами. С другой стороны, при повторных поисках нефти в

какой-либо области могут представить интерес небольшие структурные аномалии, так как заранее

известно, что более крупные структуры данной области уже изучены. В этих условиях закономерно-

сти, выявляемые на таких мелких структурах, следует рассматривать как «региональный тренд».

Для иллюстрации рассмотрим график, изображенный на рис. 5.72,а. В представленной си-

туации можно различными способами выделить «региональную» и «локальную» компоненты. До-

пустим, что региональный тренд характеризуется прямой линией, проходящей через совокупность

точек наблюдения. Тогда все наши данные можно разделить на линейный тренд и три локальные

большие аномалии, что и показано на рис. 5.72,б. Однако может оказаться, что для описания тренда

параболическая функция будет более представительна, чем уравнение прямой линии. На рис. 5.72,в

показано такое разделение на компоненту параболического тренда и локальные отклонения, что

значительно отличается от ситуации, изображенной на рис. 5.72,б. Можно принять и более сложную

функцию для описания тренда, например кубическую, которая приведет к еще меньшей величине

аномалий (рис. 5.72,г). Возможна и такая ситуация, когда результаты опробования и кривая тренда

будут совпадать, так что остаток будет отсутствовать. Конечно, в этом случае нельзя провести раз-

деление на «региональную» и «локальную» компоненты и такое исследование потеряет смысл.

Рис. 5.72. Двумерная иллюстрация

понятия тренда: а – множество дан-

ных точек и линия, на которой они

расположены; б – прямая линия, по-

добранная к наблюдениям; в – пара-

болический тренд; г – кубический

тренд. Заштрихованная область соот-

ветствует отрицательному и положи-

тельному отклонениям от линии

тренда

После всего того, что бы-

ло сказано, вполне естественен

вопрос: можно ли по результатам

наблюдения получить объектив-

ное выделение двух компонент,

если само определение этих ком-

понент в значительной степени

субъективное. Ответ на этот во-

прос будет положительным, если

вместо геологического определе-

ния тренда и отклонения восполь-

зоваться операционным опреде-

лением, которое фиксирует способ обработки данных. Например, тренд можно определить как ли-

нейную функцию географических координат, построенную по набору наблюдений так, что сумма

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

квадратов отклонений их от тренда минимальна. Рассмотрим более подробно три части этого опре-

деления.

1. Определение основано на понятии географических координат. Это значит, что результат наблю-

дения (абсолютная отметка местности, содержание золота в жиле и др.) рассматривается как

функция положения наблюдения в пространстве.

2. Тренд рассматривается как линейная функция. Это значит, что уравнение, описывающее тренд,

имеет форму Y = b

+ b

+ ..., где b – коэффициенты, а Х – географические координаты.

Уравнение будет включать значения Y, которые будут результатами наблюдения.

3. Требование минимизации суммы квадратов отклонений от тренда подробно описано в гл. 2 (см.

кн. 1) применительно к дисперсии. Дело в том, что сумма квадратов отклонений результатов на-

блюдений от среднего характеризует выборочную дисперсию. Если вместо среднего подставить

уравнение прямой линии или плоскости, то тогда, рассматривая это уравнение как функцию

дисперсии, можно выбрать такой его вариант, который бы минимизировал сумму квадратов от-

клонений. Необходимо отметить, что определение уравнения линейной регрессии весьма сходно

с только что приведенным определением. Вообще тренд-анализ можно рассматривать как один

из вариантов статистического метода множественной регрессии, и поэтому все приемы обработ-

ки данных взяты непосредственно из регрессионного анализа. В некоторых случаях при реше-

нии геологических задач будут проверяться гипотезы, связанные с множественной регрессией.

В гл. 4 (см. кн. 1) была построена линия регрессии Y на X, которая являлась линией наилуч-

шей оценки Y для любого заданного значения X. Уравнение прямой Y = b

+ b

Х находилось путем

решения системы нормальных уравнений:



Y = b

n + b





XY = b



X + b



(5.82)

относительно неизвестных коэффициентов b

, b

. Суммирование в этих и последующих уравнениях

проводится от i=1 до n. Для простоты запись пределов суммирования опущена.

Эту систему уравнений легко приспособить, если имеется два аргумента, например такие,

как географические координаты, в результате чего получим уравнение линейной поверхности трен-

да:

Y = b

+ b

. (5.83)

В данном случае результат геологического наблюдения рассматривается как линейная функ-

ция двух координат Х

и Х

с коэффициентами b

, b

, оценить которые можно с помощью систе-

мы следующих уравнений:

  





22211202

212

11101

22110

XbXXbXbYX

XXbXbXbYX

XbXbnbY

(5.84)

Решив уравнения (5.84) относительно b

, b

, найдем их оценки. Этот метод нахождения

оценок называется методов наименьших квадратов.

Уравнения (5.84) можно записать в матричной форме:















































XXXX

XXn

2212

(5.85)

Сходство между матричным уравнением (5.85) и уравнением (4.33) очевидно. Оба эти урав-

нения можно рассматривать как приближенные характеристики функции двух аргументов, которые

в данном случае являются географическими координатами X

и Х

. При подборе кривой второго по-

рядка в рассмотренном выше примере также рассматривались две переменные Х и X

, и задача была

сведена к решению системы линейных уравнений. Таким образом, между этими двумя процедурами

нет принципиальной разницы. В качестве примера построения линейной поверхности тренда рас-

смотрим следующую задачу.

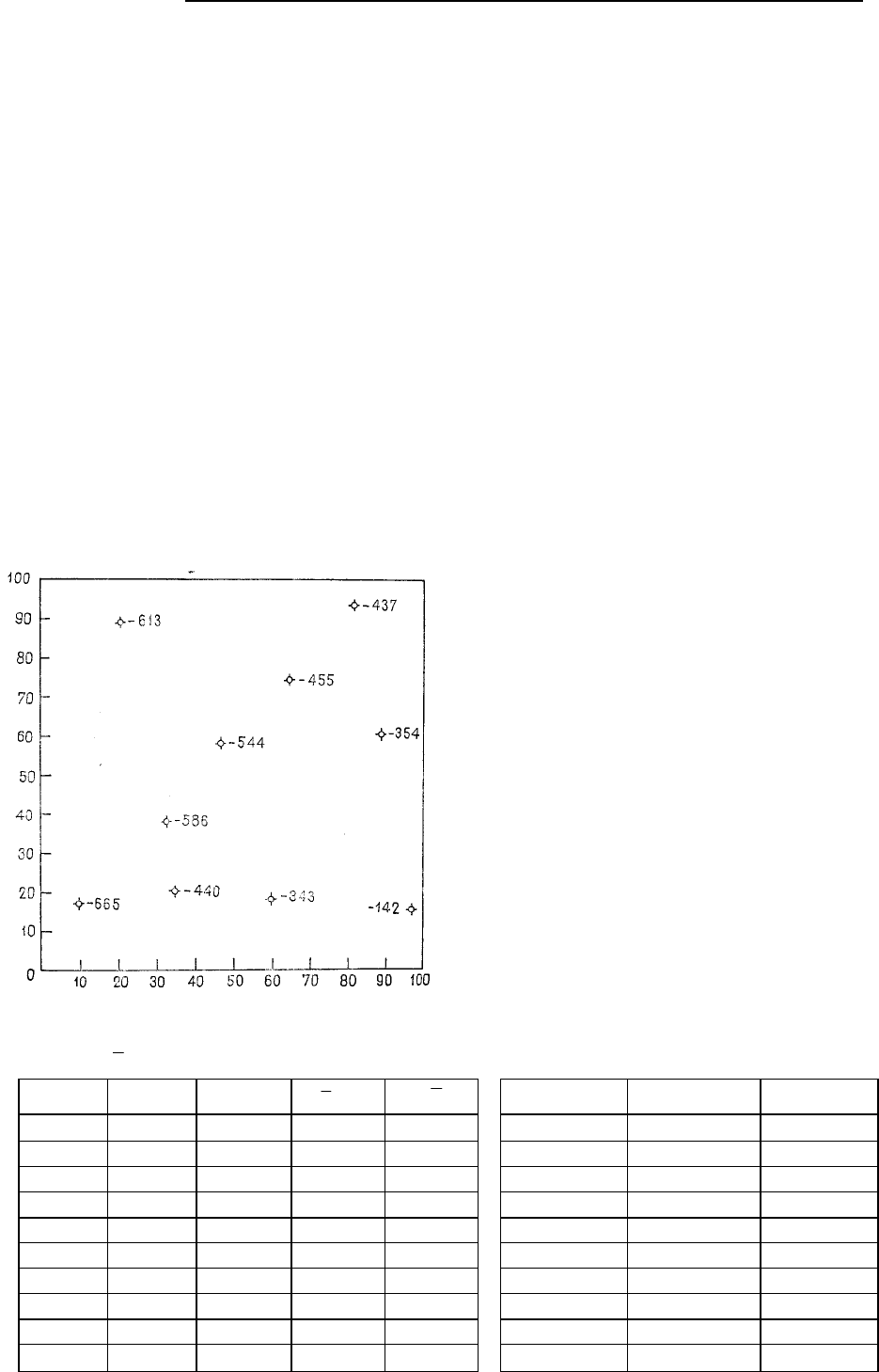
Одна английская нефтяная компания приобрела концессию в весьма удаленной части Севе-

ро-Восточной Африки. Территория была крайне необжитой, труднодоступной и почти полностью

геологически неизученной. По условиям концессии компания должна была пробурить в течение го-

да десять скважин или в случае невыполнения этого условия потерять свои права. Руководство ком-

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

пании приняло решение бурить серию далеко расположенных друг от друга разведочных скважин,

предназначенных для создания геологической основы, необходимой для продолжения поисков. На

рис. 5.73 показано расположение этих скважин на территории концессии, общая площадь которой

составляла 100 км

. Координаты скважин, отсчитываемые в километрах от юго-западного угла тер-

ритории, и абсолютные отметки подошвы меловых отложений, зафиксированные в скважинах, при-

ведены в табл. 5.15. Задача в данном случае заключается в построении линейной поверхности трен-

да и выявлении областей положительных отклонений от нее, которые можно рассматривать как за-

служивающие внимания для проведения дополнительных исследований.

Для построения поверхности тренда мы должны сначала подсчитать суммы значений X

, Х

и Y, суммы квадратов X

и Х

, а также суммы соответствующих смешанных произведений, т.е. чис-

ла, требуемые формулой (5.84)











23234227030

2110983169236934

4579482539

221

YXXX

YXX

Подставив эти значения в формулу (5.85), получим











































232342

211098

4579

3169227030482

2703036943539

48253910

Рис. 5.73. Карта расположения скважин и абсо-

лютных отметок подошвы меловых отложении

в Северо-восточной Африке. По данным нефтя-

ной компании Англо-Баррен Ойл Кампани. От-

метки даны в метрах ниже уровня моря. За едини-

цу выбран километр; отсчет координат ведется от

юго-западного угла карты

Таблица 5.16. Координаты, абсолютные отметки

подошвы меловых отложений, их оценки Y и раз-

ность





YY 

Таблица 5.15 Координаты скважин и воз-

вышений оснований мелового периода в

пределах нефтяной концессии

, км Х

, км Y, м

, м





YY 

,м

, км X

, км Y, м

10,0 17,0 –665,0 –606,6 –58,3 10,0 17,0 –665,0

21,0

89,0

–

613,0

–

695,7

82,7

21,0

89,0

–

613,0

33,0

38,0

–

586,0

–

537,8

–

48,1

33,0

38,0

–

586,0

35,0

20,0

–

440,0

–

492,8

52,8

35,0

20,0

–

440,0

47,0

58,0

–

544,0

–

510,2

–

33,7

47,0

58,0

–

544,0

60,0

18,0

–

343,0

369,3

26,2

60,0

18,0

–

343,0

65,0

74,0

–

455,0

–

455,5

0,5

65,0

74,0

–

455,0

82,0

93,0

–

437,0

–

411,5

–

25,4

82,0

93,0

–

437,0

89,0

60,0

–

354,0

–

313,0

–

40,9

89,0

60,0

–

354,0

97,0 15,0 –142,0 –186,0 44,1 97,0 15,0 –142,0

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Решить это матричное уравнение можно методом, описанным в гл. 3 (см. кн. 1). Решение бу-

дет следующим:

= –621,0, b

= 4,8, b

= –2,0.

Подставив эти значения коэффициентов в уравнение

Y = b

+ b

можно вычислить теоретические значения Y для каждой из десяти скважин, которые вместе с разно-

стями





YY  приведены в табл. 5.16.

Кроме того, можно охарактеризовать качество приближения поверхности тренда к наблю-

даемым результатам, используя формулы с (4.18) по (4.24), введенные для случая линии. В частно-

сти, мы можем охарактеризовать общую изменчивость, вычислив сумму квадратов для Y, т.е.

 

9,215324

1 2



 

YSS

Для того чтобы получить аналогичную характеристику для Y в табл. 5.16, мы должны вы-

числить сумму квадратов, возникающую из уравнения регрессии





 

 4,193861

1 2

YSS

Разность между этими величинами будет характеризовать изменчивость отклонений от по-

верхности тренда:

= SS

– SS

= 21463,5.

Таким образом, поверхность тренда учитывает следующий процент общей изменчивости:

100% R

= (SS

)/(SS

) = 90,0%.

Коэффициент множественной корреляции в данном случае составит 95,0

 RR .

Из полученных крайне высоких значений можно сделать вывод о том, что подошва меловых

отложений изучаемой территории является почти ровной и описывается постепенно погружающей-

ся плоскостью. Как видно из табл. 5.16, отклонения от теоретической плоскости весьма малы. Все

это наглядно представлено на рис. 5.74, где приведена карта подошвы меловых отложений.

Хотя этот простейший вид анализа является удовлетворительным в данном примере, вполне

возможны ситуации, когда плоскости будет недостаточно для описания геологического тренда, ко-

торый может быть весьма сложным. Более того, мы очень редко располагаем априорными сведе-

ниями о форме функции, описывающей тренд. Физики, например, могут заранее сказать, что бро-

шенный камень полетит по параболе, так как они располагают некоторыми сведениями о факторах,

контролирующих этот процесс, т.е. об ускорении свободного падения и др. Геологи крайне редко

могут говорить априори о наилучшей форме функции, описывающей поверхность тренда. Самое

лучшее, что они могут сделать, – это проводить последовательные приближения к неизвестной

функции, начиная с некоторой функции произвольной формы. В частности, они расширяют воз-

можности представления линейной поверхности с помощью полиномов, вводя степени выше первой

и смешанные произведения географических координат. Полиномы исключительно чувствительны,

и, если использовать их достаточно высокие степени, с их помощью можно описывать весьма слож-

ные поверхности.

Необходимо отметить, что полиномиальные функции используются в тренд-анализе глав-

ным образом как удобное средство описания полученных данных. При этом уравнения, по которым

отыскиваются полиномиальные коэффициенты, легко строятся и решаются на ЭВМ.

Применение полиномов может привести к мнению, что геологические процессы являются

полиномиальными функциями и даже их линейными вариантами. Нужно помнить, что природа этих

процессов остается неизвестной и с помощью полиномов может быть описана только приближенно.

В отдельных примерах могут быть более приемлемы и другие варианты приближения, что будет

рассмотрено в данном разделе.

Как уже отмечалось в гл. 4, метод наименьших квадратов может быть применен не только к

уравнению прямой, но и к кривой второго (и более высокого) порядка путем добавления соответст-

вующих компонент:

Y = b

+ b

. (5.86)

Поверхность тренда второго порядка будет описываться уравнением

Y = b

+ b

. (5.87)

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Заметим, что эти уравнения содержат такие компоненты, как квадраты географических ко-

ординат и их смешанное произведение. Перейти от этого уравнения к уравнению более высокого

порядка сравнительно легко. Для этого каждая географическая координата просто возводится в за-

данную степень и добавляются соответствующие смешанные произведения. Например,

Y = b

+ b

(5.88)

представляет собой уравнение поверхности тренда третьей степени. В этом уравнении членам пер-

вой степени соответствуют коэффициенты b

и b

. Коэффициенты b

, b

и b

соответствуют членам

второй степени и стоят перед переменными, которые имеют следующую структуру:

= (X

X

), X

= (X

X

), X

= (Х

X

Таким образом, новые переменные представляют собой различные варианты произведений

исходных переменных. Аналогично коэффициенты b

, b

и b

соответствуют компонентам

третьей степени, которые имеют следующую структуру:

= (X

X

), Х

= (X

Х

X

), X

= (X

X

) и Х

= (Х

Х

Разведчики нефти нашли хорошее применение тренд-анализа поверхностей при поисках

нефти и газа в Центральной Альберте (Канада). Нефтеносный бассейн в Альберте обширен, причем

нефть локализуется как в нижнемеловых отложениях, так и в более глубоких карбонатных рифах

верхнего девонского возраста. Естественно, большее количество скважин достигает меловых обра-

зований, меньшее – девонских, особенно вблизи от передней гряды Скалистых гор, где прогнозы

глубинности рифов составляют 15000 футов или больше. Девонские рифы представлены мощной

толщей карбонатов ледукской формации, переслаивающихся и фациально замещающихся сланцами

лагунного и морского генезиса – кластическими образованиями. Карбонатные рифы не были уплот-

нены, в то время как переслаивающиеся с ними мелкозернистые пластические образования – сланцы

Айртона были уплотнены до их первоначальной мощности по мере опускания бассейна и продол-

жения образования месторождения. Это дифференциальное уплотнение создано складчатыми

структурами над погребенными рифами; эти структуры сохраняются в вышележащих породах, хотя

их величины уменьшаются на более мелких горизонтах.

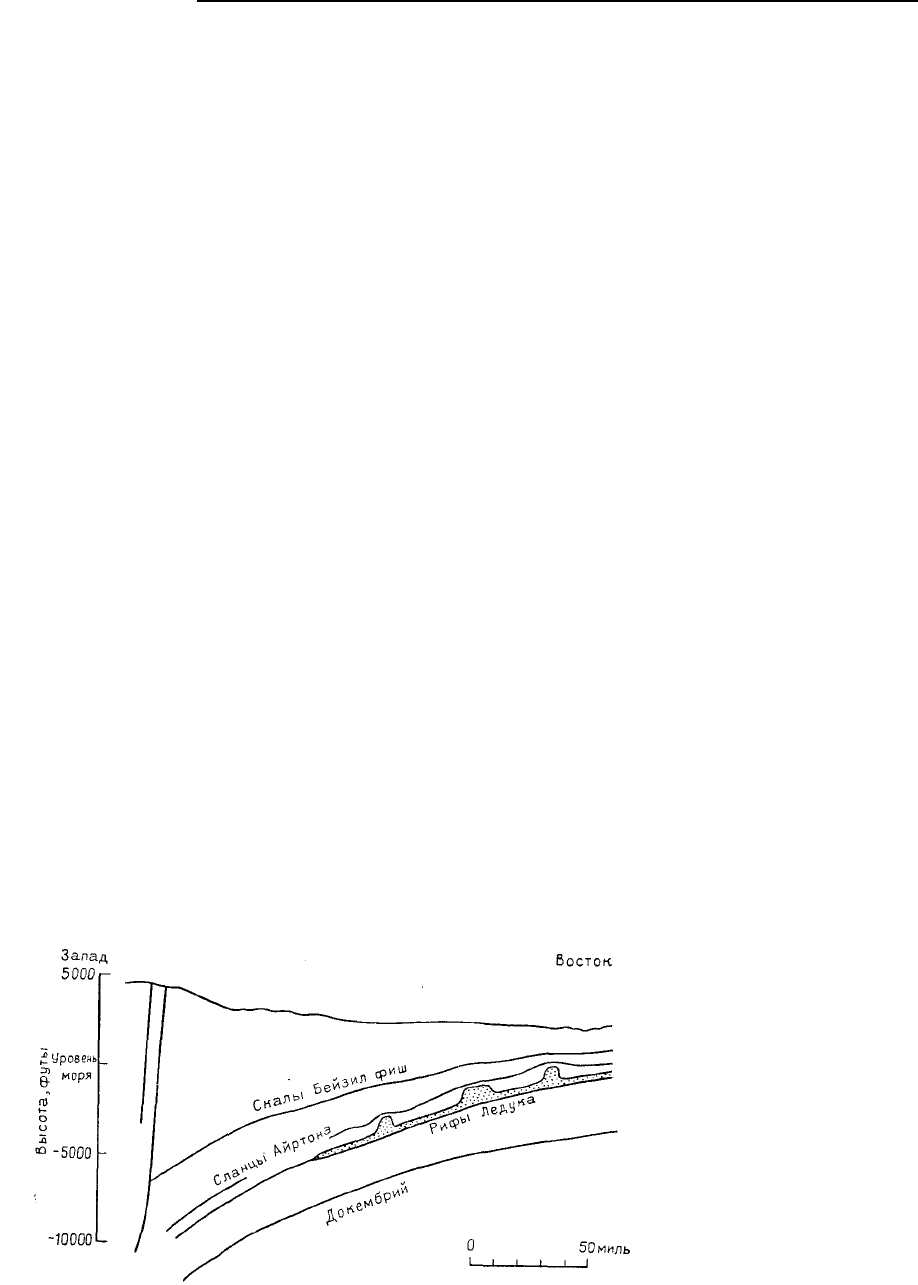
Глубокозаложенные черты уплотнения не являются очевидными на меловых горизонтах из-

за пугающего эффекта сильного регионального наклона пласта (рис. 5.75). Замкнутость на глубине

выражается только как слабые изменения локального градиента, который на структурных картах

меловых горизонтов выглядит как слабое изменение в расположении изолиний. Однако если эта

компонента сильного регионального наклона может быть устранена на этих картах, то гипотетиче-

ские нижележащие складчатые структуры выглядят замкнутыми. Так как плотность скважин в ос-

нованиях меловых отложений относительно высока, их анализ может дать ценную информацию о

возможных прогнозах в девонских пластах, хотя некоторые скважины и проникают в более глубо-

кие горизонты.

Рис. 5.75. Изображение разре-

за западного поля бассейна

Альберта в виде диаграммы.

Рифы Ледука и сланцы Айрто-

на верхнего девона; скалы Бей-

зил-Фиш сложены нижнемело-

выми породами

Скалы Бейзил-Фиш

состоят из черного сланца,

встречающегося вблизи гра-

ницы между нижним и верх-

ним меловыми пластами.

Это место характеризуется многочисленными бентонитовыми образованиями, которые дают зага-

дочные пики при каротаже в гамма лучах из-за их высокой радиоактивности. Бентониты синхронны

и потому образуют отличные маркеры для региональной корреляции. Вершина скал Бейзил-Фиш

может быть отмечена с исключительной точностью по каротажу благодаря заметному отражению от

мощных бентонитов. Карта, представленная на рис. 5.76, охватывает площадь около 3500 квадрат-

ных миль на западе Центральной Альберты и была построена при использовании пика этих бенто-

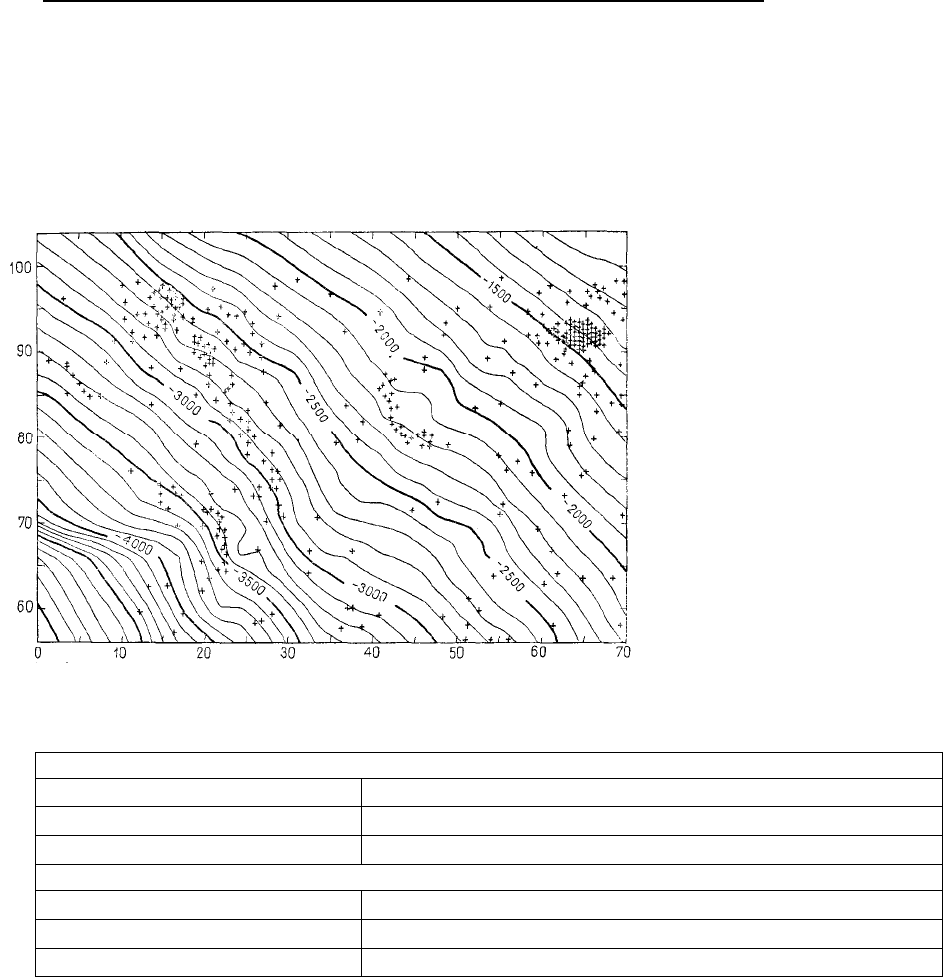
Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

нитов в верхней точке скал Бейзил-Фиш в 360 разведочных скважинах. Картируемая площадь рас-

положена на западном крае бассейна Альберта непосредственно в передней части складчатой зоны,

отделяющей фронт Скалистых гор. Аппроксимируется погружение оснований вниз к юго-западу с

увеличением погружения в западной ветви бассейна. В пределах картируемой площади глубины

скал Бейзил-Фиш изменяются от слабого с эксцессом в 1000 футов ниже уровня моря на северо-

востоке, вплоть до 5000 футов ниже уровня моря на северо-западе.

Рис. 5.76. Структурная кар-

та вершины скал Бейзил-

Фиш, бассейн Альберта.

Изолинии указаны в футах

ниже уровня моря. Крестики –

контрольные скважины

Таблица 5.17 Статистики полиномиальной тренд-поверхности первой и второй степеней, подго-

няемые к возвышениям Бейзил-Фиш в центре Западной Альберты

Тренд

поверхность пер

вой степени:

процент соответствия (R

)

98,6%

Коэффициент корреляции (R)

0,993

Уравнение поверхности тре

да:

Y= –635,4 + 29,3X

+ 33,8Х

Тренд

поверхность второй степени:

процент соответствия (R

)

99,7%

Коэффициент корреляции (R)

0,999

Уравнение пове

рхности тре

да:

Y= –7993,3 + 63,4Х

+ 59,2X

– 0,1Х

– 0,3X

– 0,1Х

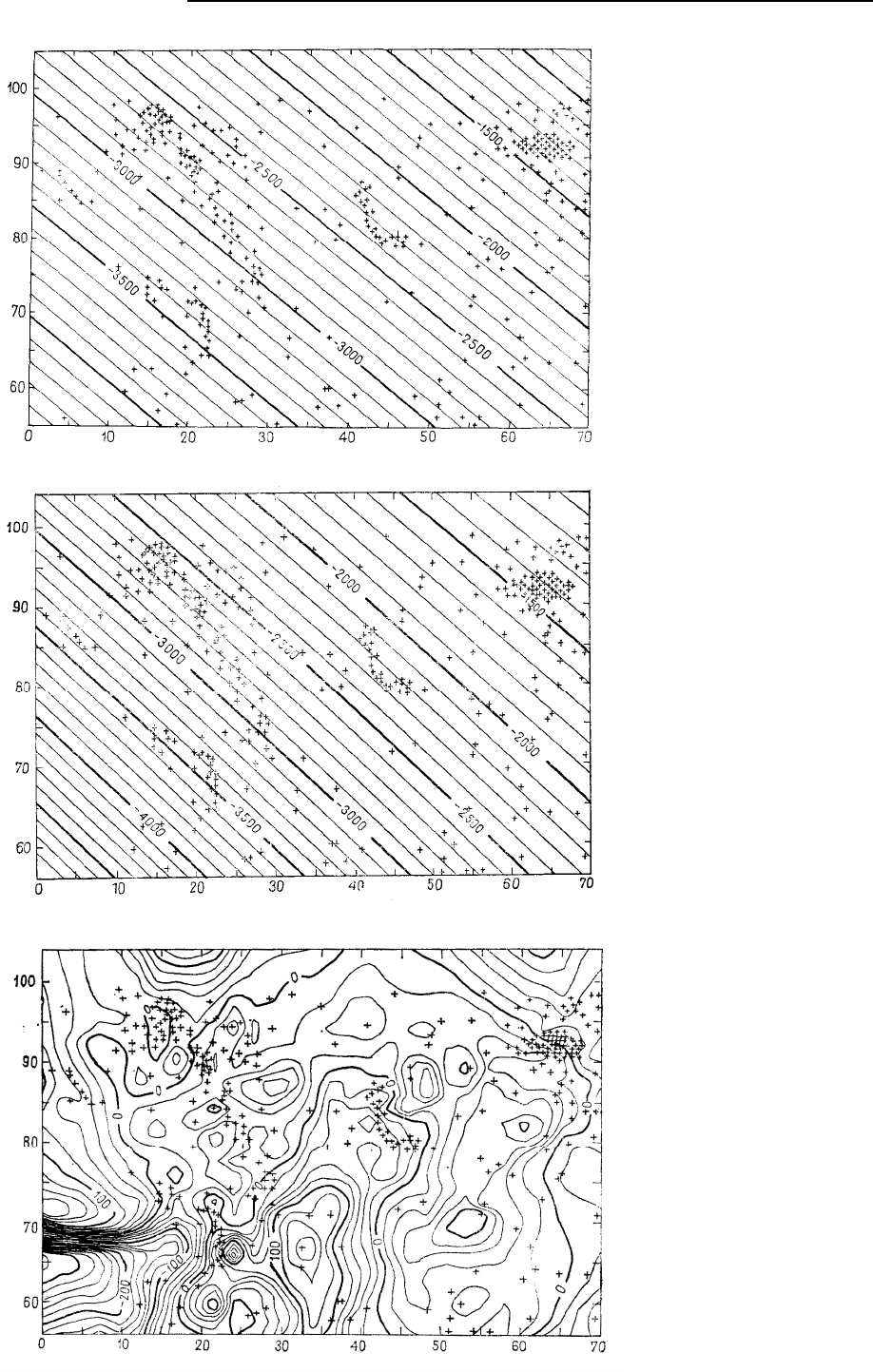
На рис. 5.77 и 5.78 представлены полиномиальные поверхности тренда первого и второго

порядков для скал Бейзил-Фиш; значения статистик, характеризующих подбор поверхностей тренда,

приведены в табл. 5.17. Обе тренд-поверхности обеспечивают очень высокую точность аппроксима-

ции наблюдений, хотя поверхность второй степени дает значительно более точное приближение,

чем поверхность первой степени. В этом примере для выбора степени поверхности тренда статисти-

ческие критерии значимости неприменимы, так как проблема состоит не только в статистической

оценке. Цель скорее состоит в более точном моделировании региональных черт структурной кон-

турной карты, и потому вычитание тренда помогает устранить региональные компоненты структу-

ры. Действительно, поверхность тренда используется как фильтр высокой пропускной способности,

устраняющий крупномасштабные структурные вариации из карты и сохраняющий мелкомасштаб-

ные характерные черты.

На рис. 5.79 изображены остатки от тренд-поверхности второй степени. Рис. 5.80 – это па-

леографическая карта верхнего девона, реконструированная по скважинам и сейсмической инфор-

мации. Заметно сильное совпадение между положительными остатками тренда на скалах Бейзил-

Фиш и положениями Больших девонских рифов, в частности рифов Вайндфолл. После устранения

регионального тренда остаются последовательные изолированные более мелкие компоненты струк-

тур, представляющих складки над этими рифами. Несколько крупных нефтяных полей на этой пло-

щади были открыты с помощью данного метода.

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Рис. 5.77. Поверхность трен-

да первой степени, постро-

енная для скал Бейзил-

Фиш. Изолинии указаны в

футах ниже уровня моря

Pиc. 5.78. Поверхность трен-

да второй степени, построен-

ная для скал Бейзил-Фиш.

Изолинии указаны в футах

ниже уровня моря

Рис. 5.79. Карта разностей

значений структурной кар-

ты скал Бейзил-Фиш (см.

рис. 5.78) и тренда второй

степени (см. рис. 5.75). Кре-

стиками заштрихованы об-

ласти, соответствующие по-

ложительным разностям.

Интервал между изолиниями

20 футов