Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Подождите немного. Документ загружается.

ственно из полувариограммы или из математических функций, описывающих ее вид.

Определив неизвестные веса, значение оцениваемой переменной в точке р представим в ви-

де

33221

YWYWYWY

 . (5.78)

Оценка дисперсии имеет вид



= W



1р

) + W



) + W



2р

) +



(5.79)

Иными словами, дисперсия оценки есть в сущности взвешенная сумма полудисперсий для

расстояний до точек, использованных в оценивании, плюс вклад от коэффициента К, который экви-

валентен постоянному члену. Крайгинг имеет два больших преимущества перед обычными проце-

дурами оценивания, которые используются при построении карт в изолиниях. Оценки процедур

крайгинга в среднем имеют наименьшую возможную ошибку, и также обеспечивают явное выраже-

ние величины этой ошибки.

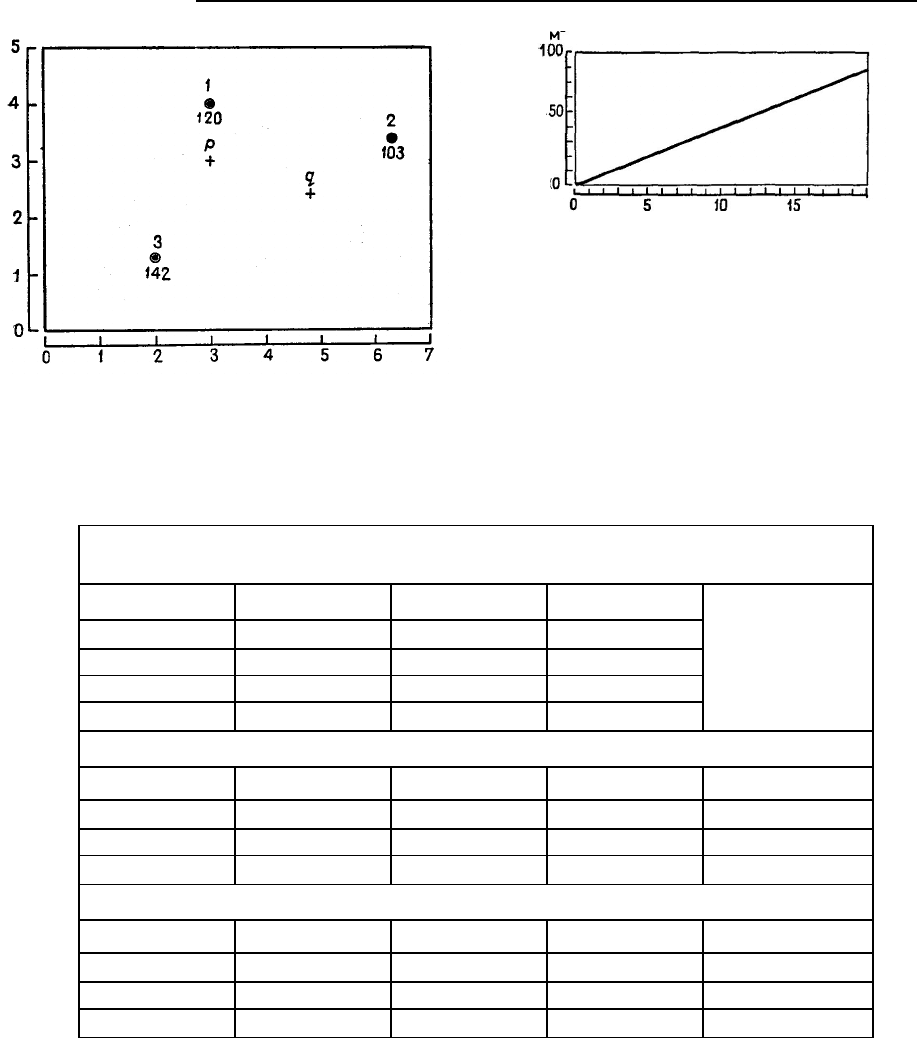
Для иллюстрации точечного крайгинга мы приведем оценку уровня воды в точке р на карте,

представленной на рис. 5.63. Оценка будет проведена по известным уровням, измеренным в трех

наблюдательных скважинах. Координаты карты скважин и расстояния между ними приведены в

табл. 5.12. Предварительный структурный анализ позволил получить линейную полувариограмму

(рис. 5.64). Значения полудисперсии, соответствующие расстоянию между скважинами, даны в табл.

5.12; они могут быть получены прямо из полувариограммы или вычислены из наклона.

Уравнения, которые должны быть решены для определения весов, в этом примере имеют

вид

0,10

9,7)0()1,18()5,11(

1,12)1,18()0()2,12(

0,4)5,11()2,12()0(

321



WWW



или в матричной форме









































0,1

9,7

1,12

0,4

00,10,10,1

0,101,185,11

0,11,1802,12

0,15,112,120



Матрицу, обратную к матрице левой части, можно найти с помощью метода, изложенного в

гл. 3 (см. кн.1), но в целях упрощения вычислений целесообразно поменять порядок уравнений для

того, чтобы избежать нулей на диагонали. Обратная матрица есть















5851,93995,04072,01932,0

3995,00461,00106,00354,0

4072,00106,00433,00326,0

1932,00354,00326,00680,0

Теперь можно найти неизвестные веса умножением справа на транспонированную матрицу

вектора правой части, состоящего из полудисперсий. В результате получим





























7298,0

3071,0

0975,0

5954,0



оценка уровня воды в точке р находится подстановкой подходящих весов в линейное уравнение

(5.78):

1,125)142(3071,0)103(975,0)120(5954,0 

Y м.

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Рис. 5.64. Линейная полувариограмма уровней

воды на площади, включающей карту рис. 5.63.

Полувариограмма имеет наклон 4,0 м

/км внутри

20-километровой зоны.

Рис. 5.63. Карта уровней воды (в м) в трех наблю-

дательных скважинах. Оценки уровня воды сделаны

в точках р и q. Координаты указаны (в км) для произ-

вольного начала

Таблица 5.12

Наблюдения, проведенные в скважинах, используемых для оценки уровня воды в

точке р

Скважина

Координата X

Уровень воды

1 3,0 4,0 120

6,3

3,4

103

2,0

1,3

142

Точка р 3,0 3,0

Расстояния между скважинами и точкой р

Скважина 1 2 3

1 0 3,35 2,88 1,00

4,79

3,32

0 1,97

Полудисперсии для расстояний между скважинами и точкой р

Скважина 1 2 3

1 0 13,42 11,52 4,00

19,14

13,30

3 0 7,89

Аналогично находится и ошибка дисперсии во взвешенной сумме полувариограмм для рас-

стояний от контрольных точек до оцениваемой точки. В матричных обозначениях s



=[W][B]:



=0,5954(4) + 0,0975(12,1) + 0,3071(7,9) – 0,7298(1) = 5,25 м

Стандартная ошибка оценки есть просто квадратный корень из оценки дисперсии или





5,25=2,3 м. Если мы предположим, что ошибки оценивания распределены нормально относи-

тельно истинного среднего значения, то мы можем использовать стандартную ошибку для опреде-

ления доверительного интервала этой оценки. Вероятность того, что истинный уровень воды в точке

р находится в пределах одной стандартной ошибки выше или ниже оцениваемого значения, равна

68%, а вероятность того, что истинный уровень лежит в пределах двух стандартных ошибок, равна

95%. Иными словами, уровень воды в точке должен быть Y

= 125,1 ± 4,6 м с вероятностью 95%. В

каждой точке этой карты мы можем оценить уровень воды и можем также определить стандартные

ошибки этих оценок. Из них мы можем построить две карты; первая основана на самих оценках и

является наилучшим образом предсказанной конфигурацией картируемых переменных, вторая – это

ошибка карты, показывающая доверительную обертывающую поверхность, которая окружает оце-

ниваемую поверхность; она выражает относительную надежность первого отображения. На площа-

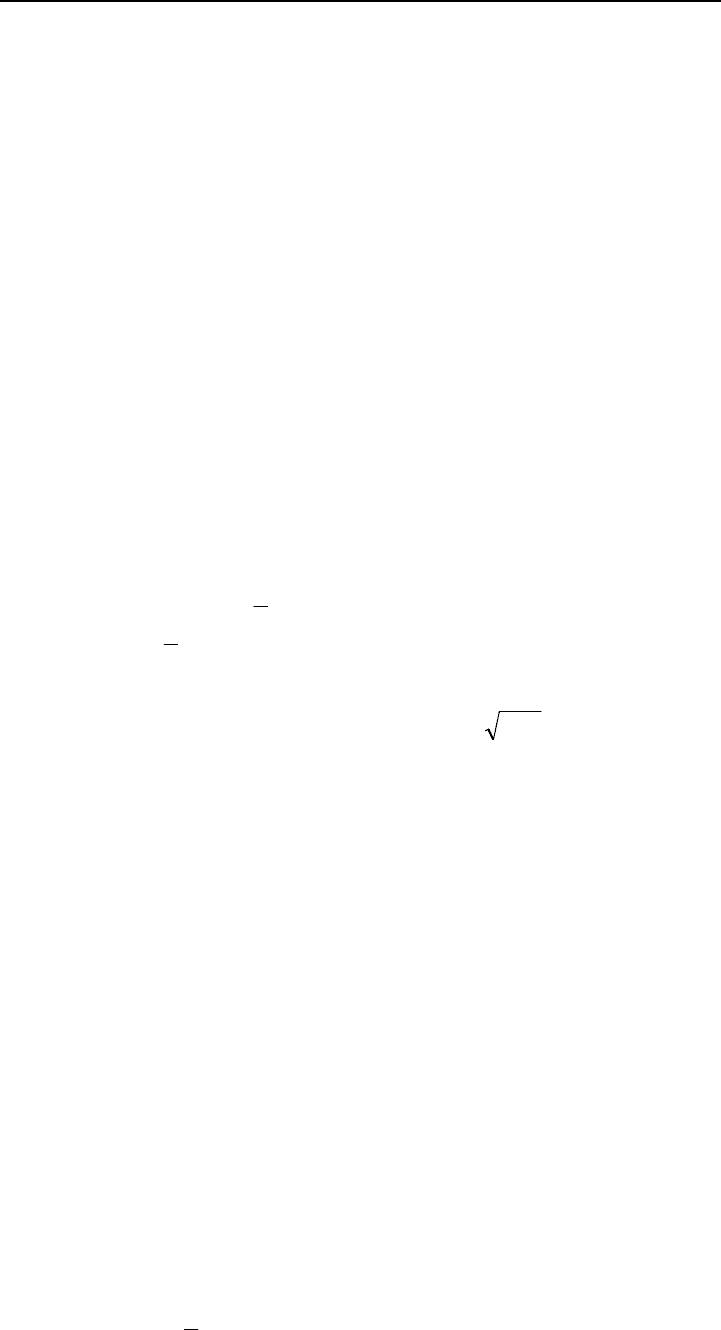
Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

дях слабого контроля ошибка карты может принимать большие значения, показывая, что оценивае-

мый параметр подвергается большой изменчивости. На площадях слабого контроля ошибка карты

будет показывать низкие значения, и в самих контрольных точках ошибка оценки будет равна нулю.

Система уравнений, используемая для нахождения весов крайгинга, должна решаться для

каждой оцениваемой точки до тех пор, пока пробы расположены по регулярной схеме так, что рас-

стояния между точками остаются одинаковыми. Если мы пожелаем оценить уровень воды в точке q

на рис. 5.63, то необходимо рассмотреть расстояния между q и тремя наблюдаемыми скважинами.

Эти расстояния и соответствующие полудисперсии, взятые из рис. 5.64, следующие:

























0,12

2,6

6,9

;

0,3

6,1

4,2

Так как расположение наблюдаемых скважин остается тем же самым, то все расстояния ме-

жду ними одинаковы и левая часть системы совместных уравнений неизменна. Обратная матрица

тоже не изменяется. Поэтому, умножив ее на новый вектор полудисперсий, мы получим веса для

оценки уровня воды в точке q. Новое множество весов таково:





























3711,0

2528,0

5796,0

1676,0



Оценим уровень воды

Y и дисперсию s



Y = 0,1676(120) + 0,5796(103) – 0,2528(142) = 115,7 м;



= 0,1676(9,6) – 0,5796(6,3) + 0,2528(12,0) – 0,3711(1) = 7,91 м

Стандартная ошибка оценки в точке 8,291,7 



sq м, поэтому уровень воды в этой

новой точке может быть выражен в виде Y

= 115,7 ± 5,6 м с вероятностью 95%. Поверхность под-

земных вод в точке q ниже, чем в точке р, и стандартная ошибка больше, что отражает большое об-

щее расстояние до контрольных скважин.

Если одна из контрольных точек изменяется, то некоторые из расстояний также изменяются,

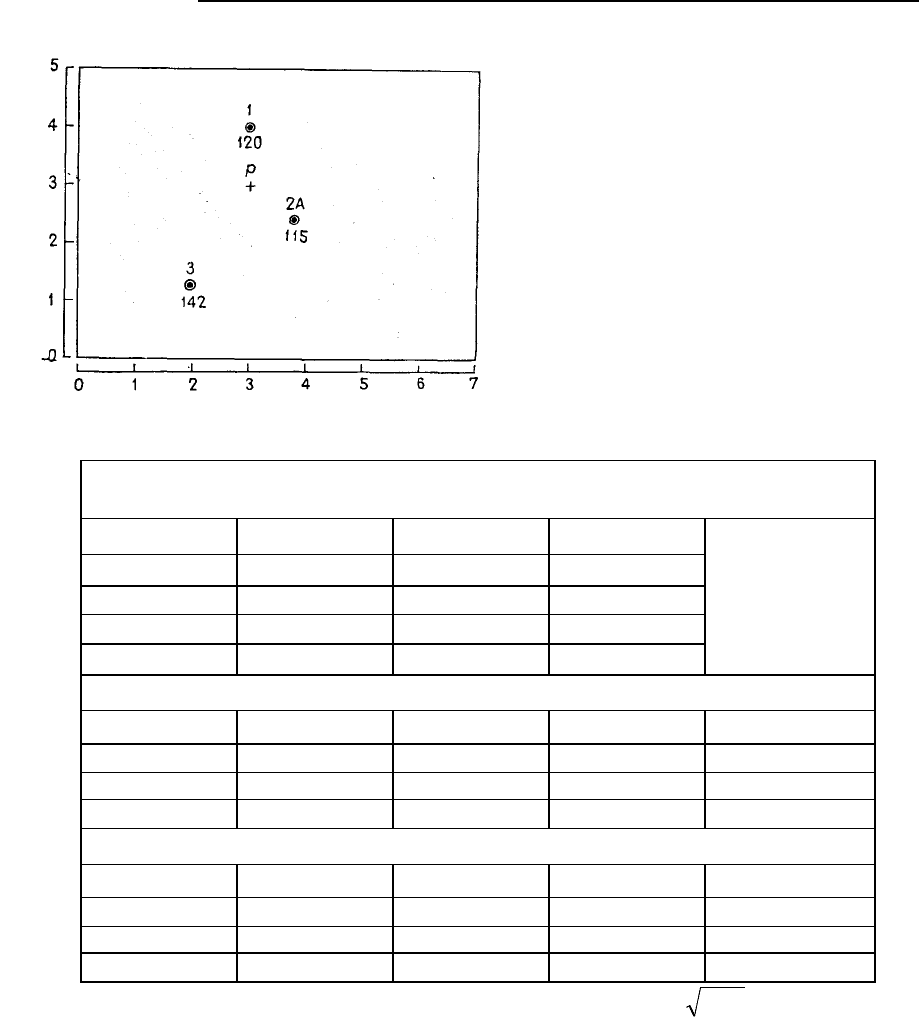
и система уравнений должна быть решена заново. На рис. 5.65 наблюдаемая скв. 2А была пробурена

в точке, более близкой к точке р, и для регионализованной переменной, характеризующей уровень

воды, было замерено значение 115 м. Новые расстояния между точками и соответствующие полу-

дисперсии приведены в табл. 5.13. Система уравнений теперь имеет вид









































0,1

9,7

0,4

00,10,10,1

0,104,85,11

0,14,802,7

0,15,112,70



а решение этой системы





























6001,0

1598,0

3858,0

4545,0



Новая оценка (в м) уровня воды в точке р, основанная на информации по скв. 2А, имеет сле-

дующий вид:

6,121)142(1598,0)115(3858,0)120(4545,0 

Дисперсия этой новой оценки (в м

)



= 0,4545(4,0) + 0,3858(4,0) + 0,1598(7,9) – 0,6001(1) = 4,02.

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Рис. 5.65. Карта, показывающая уровни

воды (в м) в трех наблюдательных сква-

жинах. Скважина 2А ближе к оцениваемой

точке р, чем скважина 2 на рис. 5.63

Таблица 5.13. Второй ряд наблюдений, проведенных в скважинах, используемых

для оценки уровня воды в точке р

Наблюдения, проведенные в скважинах, используемых для оценки уровня воды в

точке р

Скважина

Координата X

Уровень воды

3,0 4,0 120

2А

3,8

2,4

115

2,0

1,3

142

Точка р

3,0 3,0

Расстояния между скважинами и точкой р

Скважина

1 2А 3 Р

1 0 1,79 2,88 1,00

2,11

1,00

0 1,97

Полудисперсии для расстояний между скважинами и точкой р

Скважина

1 2A 3 р

1 0 7,16 11,52 4,00

8,44

4,00

0 7,89

Стандартная ошибка (в м) в точке р теперь будет равна 0,202,4





s , что несколько

ниже, чем было найдено на основе наблюдений скважины 2, а не 2А. Это иллюстрирует тот факт,

что ошибки оценки уменьшаются, если контрольные точки располагаются ближе к оцениваемой

точке.

Предположим, что одна из контрольных точек совпадает с точкой, в которой производится

оценка. Тогда одно из значений правой части матричного уравнения равно нулю; оставшиеся значе-

ния становятся равными некоторым из значений матрицы, стоящей в левой части. Предполагая, что

наблюдаемая скв. 2В пробурена в точке р, можно определить эффект от этой замены в данном при-

мере: оцененный уровень воды оказывается равным 125 м. Расстояние между любой точкой i и точ-

кой 2В теперь то же, что и расстояние между любой точкой i и точкой р. Аналогично полудиспер-

сии будут теми же, и система уравнений примет вид









































0,1

9,7

0,0

0,4

00,10,10,1

0,109,75,11

0,19,700,4

0,15,110,40



Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Можно вычислить вектор весов и, как и следует ожидать,



























0000,0

0000,1

0000,0



Если эти веса использовались для оценки точки р, то оцениваемая отметка в точности равна

измеренному значению уровня воды (в м) в скв. 2В:

0,125)142(0000,0)115(0000,1)120(0000,0 

Значит, как и следовало ожидать,



= 0,0000(4,0) + 1,0000(0) + 0,0000(7,9) + 0,0000(1) = 0,00 м

Это объясняет, что подразумевается под часто используемой характеристикой крайгинга как

точного интерполяционного метода; он действительно позволяет предсказать измеренные значения

в известных точках и делает это с ошибкой, равной нулю. Конечно, мы обычно не занимаемся оцен-

кой в точках, уже известных, но это может понадобиться в случае, если точечный крайгинг будет

использоваться для построения карты в изолиниях. Если случится, что какая-либо из контрольных

точек совпадает с узлом сети, то крайгинг даст правильные, свободные от ошибок значения. Мы

также должны быть уверены, что оцениваемая поверхность пройдет в точности через все контроль-

ные точки и что доверительные области вокруг оценки поверхности проходят через нуль в кон-

трольных точках.

С целью максимального упрощения математических выкладок в этих примерах предполага-

ется, что каждая оценка сделана на основе трех контрольных точек. На практике при получении

оценок приходится использовать больше точек, а возможно, значительно больше. Каждую кон-

трольную точку в оценке можно взвесить, и определение каждого веса требует решения своей сис-

темы уравнений. Большинство программ для получения оценки в каждом узле сети для построения

карты в изолиниях использует 16 контрольных точек или более, что приводит к необходимости ре-

шать по меньшей мере 17 систем уравнений для каждой точки. Таким образом, использование край-

гинга для построения карт в изолиниях приводит к очень трудоемким вычислениям.

В теории число точек, необходимых для получения оценки в точке, изменяется с изменени-

ем локальной плотности контроля. Для получения оценки в точке должны быть учтены все кон-

трольные точки, расположенные в окрестности этой точки. На практике многие из этих точек ока-

зываются избыточными, и их применение лишь незначительно улучшает оценку. При использова-

нии крайгинга для целей картирования в изолиниях следует руководствоваться практическим пра-

вилом, которое ограничивает число действительно необходимых контрольных точек, в пределах зо-

ны влияния или в окрестности. Оптимальное число контрольных точек определяется полуварио-

граммой и пространственной схемой расположения точек [63]. Структурный анализ, таким образом,

играет двойную роль в крайгинге: он обеспечивает получение полувариограммы, необходимой для

построения системы уравнений крайгинга, и также позволяет определить размер окрестности, внут-

ри которой для получения каждой оценки выбираются контрольные точки.

Универсальный крайгинг

Важное свойство точечного крайгинга состоит в том, что он перестает работать в случае, ко-

гда картируемая регионализованная переменная не является стационарной. В присутствии тренда

или медленного изменения среднего значения линейная оценка не будет несмещенной. Вычислен-

ные оценки будут систематически сдвигаться вверх и вниз от истинных значений, зависящих от

размещения контрольных точек и направления наклона поверхности.

Выражаясь языком геостатистики, нестационарная регионализованная переменная рассмат-

ривается как состоящая из двух компонент. Дрифт состоит из среднего или ожидаемого значения

регионализованной переменной в пределах окрестности и медленно изменяется, представляя неста-

ционарную часть поверхности. Остаток представляет собой разность между действительными изме-

нениями и дрифтом. Очевидно, если из регионализованной переменной устранить дрифт, то остатки

будут стационарными, и к ним можно применить крайгинг. Таким образом, универсальный край-

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

гинг можно считать состоящим из трех операций: первая – оценка и устранение дрифта; затем ста-

ционарные остатки крайгируются с целью получения необходимых оценок. Наконец, оцененные

остатки комбинируются с дрифтом с целью получения истинной поверхности.

Дрифт аналогичен поверхности тренда, исключая случай, когда оценка дрифта основана

только на контрольных точках внутри окрестности оцениваемой точки. В общем случае каждая ок-

рестность каждой оцениваемой точки характеризуется различным расположением контрольных то-

чек, поэтому уравнение, определяющее дрифт, должно быть решено столько раз, сколько имеется

точек. Это не так трудно, как кажется, так как уравнения крайгинга должны быть решены для каж-

дой из этих точек, и эти две операции можно комбинировать.

Определим дрифт как некоторую произвольную функцию координат контрольных точек,

например многочлен низкого порядка. Дрифт М в точке р может быть определен как многочлен ли-

бо первого (уравнение 5.80), либо второго (уравнение 5.81) порядка:









(5.80)





















(5.81)

Пусть Х

и X

– географические координаты i-й контрольной точки в пределах окрестности



– неизвестные коэффициенты дрифта, которые должны быть найдены. Однако прежде чем это

делать, необходимо провести структурный анализ с целью определения наилучшей комбинации

размера окрестности и выражения дрифта. Как отмечалось в разделе, посвященном полувариограм-

мам, это нетривиальная задача, так как модель дрифта и размер окрестности взаимозависимы.

Выражения для дрифта в качестве дополнительных ограничений можно ввести в систему

уравнений, используемую для нахождения весов крайгинга. Решая эту расширенную систему урав-

нений, мы получим оценки весов крайгинга, которые включают эффект от заданного дрифта в пре-

делах данной локальной окрестности. Выражения дрифта связывают географические координаты

каждой контрольной точки с географическими координатами крайгируемой точки. Форма модели

дрифта, размер окрестности и форма полувариограммы остатков от дрифта тесно связаны друг с

другом. Это значит, что дисперсия остатков частично зависит от несколько произвольного задания

дрифта. В универсальном крайгинге должны быть определены веса, приписываемые контрольным

точкам, а также коэффициенты дрифта. Так как оценивается большее число членов,. то в пределах

рассматриваемой окрестности следует использовать выборки контрольных точек большего объема.

Простейший пример представляет крайгинг некоторой точки, имеющий линейный дрифт и линей-

ную полувариограмму остатков от дрифта. Линейная модель дрифта, заданная уравнением (5.80),

имеет два коэффициента, поэтому в процессе оценки дрифта должны быть использованы минимум

три точки, или же мы выйдем за рамки степеней свободы.

Если мы хотим оценить методом универсального крайгинга. как дрифт, так и регионализо-

ванную переменную, то для обеспечения необходимых степеней свободы при оценке коэффициен-

тов крайгинга потребуются дополнительные контрольные точки. В противном случае процесс край-

гинга приведет к одинаковым оценкам как для дрифта, так и для крайгируемой поверхности. Целе-

сообразно выбрать пять контрольных точек, три из которых дают степени свободы для определения

дрифта, а дополнительные две – степени свободы для оценки, самой поверхности.

Пусть координаты контрольной точки с номером i обозначаются через Х

(направление с

востока на запад) и X

(.направление с севера на юг). Мы должны определить множество из пяти

весов и коэффициенты единственного ограничения (сумма весов равна 1), плюс еще двух ограниче-

ний для линейного дрифта. Для этого требуется следующая система из восьми уравнений:



) + W



) + W



) + W



) + W



) +













)



) + W



) + W



) + W



) + W



) +













)



) + W



) + W



) + W



) + W



) +













)



) + W



) + W



) + W



) + W



) +













)



) + W



) + W



) + W



) + W



) +













)

+ W

+ 0 + 0 + 0 = 1

+ W

+ 0 + 0 + 0 = X

+ W

+ 0 + 0 + 0 = X

или в матричной форме

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2









































XXXXX

XXhhhhh

2524232221

1514131211

25155545352515

24144544342414

23133534332313

22122524232212

21111514131211

)(

000

00011111

1)()()()()(









Дополнительная процедура, позволяющая упростить вычисления, состоит в переносе начала

системы координат в крайгируемую точку. Тогда координаты Х

и Х

2р

становятся равными нулю.

Это приводит к изменению всех координат X

и Х

, но не изменяет расстояний между точками, по-

этому веса крайгинга остаются неизменными.

С целью демонстрации последовательности шагов при выполнении универсального край-

гинга мы рассмотрим еще один пример, использующий данные по водоносному пласту в западном

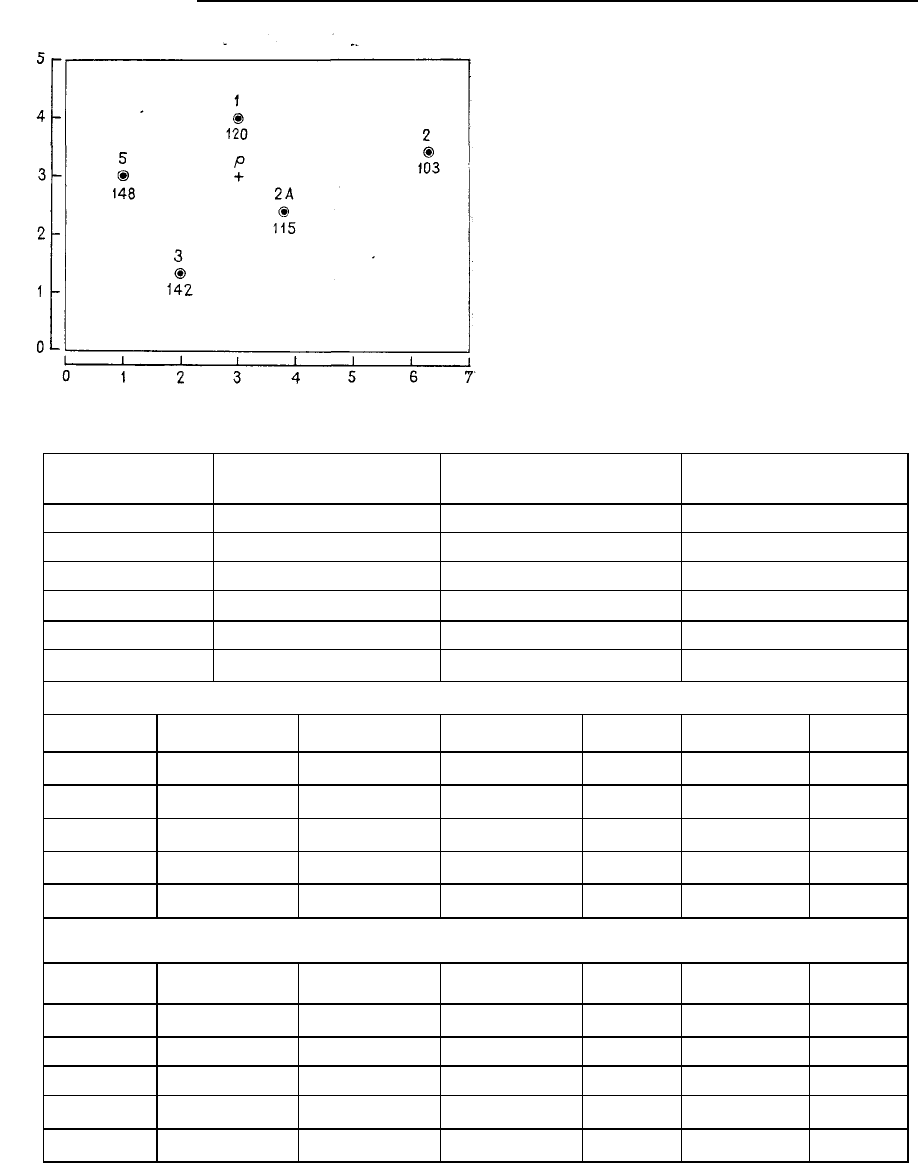
Канзасе. На рис. 5.66 изображены положения пяти наблюдательных скважин, которые будут ис-

пользованы для получения оценки дрифта и крайгируемого значения уровня воды в точке р. Пред-

положим теперь, что на рис. 5.64 представлена оценка полувариограммы остатков и что она линейна

по форме с наклоном 4,0 м

/км. Вся основная необходимая информация представлена в табл. 5.14,

которая также включает необходимые полувариограммы.

Для оценки уровня воды в точке р должно быть решено уравнение















































0,8

0,4

9,7

3,13

0,4

00006,07,14,00,1

00008,00,13,30

00011111

00,2105,119,73,219,8

6,08,015,1104,88,102,7

7,10,119,74,801,195,11

4,03,313,218,101,1904,13

0,1019,82,75,114,130





Решая это уравнение, получаем восемь коэффициентов, первые пять из которых представ-

ляют собой веса крайгинга:





























0229,0

0660,0

7245,0

0957,0

4126,0

0934,0

0137,0

4119,0

Оценка уровня воды (в м) в точке р следующая:

9,122)148(0957,0)115(4126,0)142(0934,0)103(0137,0)120(4119,0 Y ,

что лишь немногим отличается от результатов, полученных из трех наблюдений без предположения

о дрифте. Оценка ошибки дисперсии может быть вычислена в точности так же, как если бы дрифт

отсутствовал, т.е. с помощью умножения слева вектора правой части [В] на транспонированный

вектор решения [W]. Оценка дисперсии ошибки равна 8,1 м

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Рис. 5.66. Карта, на которой представлены

уровни воды (в м) в 5 наблюдательных

скважинах. Оценки уровней воды получены

методом универсального крайгинга в точке р и

в юго-западном углу карты

Таблица 5.14. Наблюдения, проведенные в скважинах, используемых для оценки уровня

воды и дрифта в точке р

Скважина

Координата Х

Координата X

Уровень воды

1 3,0 4,0 120

6,3

3,4

103

2,0

1,3

142

2А

3,8

2,4

115

1,0

3,0

148

Точка р

Расстояния между скважинами и точкой р

Скважина

1 2 3 2А 5 p

0 3,35 2,88 1,79 2,24 1,00

0 4,79 2,69 5,32 3,32

0 2,11 1,97 1,97

0 2,86 1,00

0 2,00

Полудисперсии для расстояний между скважинами и точкой p

Скважина

1 2 3 2А 5 p

0 13,42 11,52 7,16 8,94 4,00

19,14

10,77

21,26

13,30

8,44

7,89

0 11,45 4,00

0 8,00

Этот пример показывает, что нет большого различия между простым точечным крайгингом

и универсальным крайгингом с дрифтом, так как в этом примере эти две процедуры дают почти

идентичные оценки. Однако точечный крайгинг, как и другие методы взвешенного усреднения, не

может экстраполироваться за область влияния множества контрольных точек. Это значит, что

большая часть оцененных значений будет лежать на наклонных участках поверхности, и точки наи-

высших и наинизших значений на поверхности обычно будут определены контрольными точками.

Предположим, что мы оценили уровень воды в точке, причем оказалось, что поверхность вышла за

пределы интервала, определяемого наблюдаемыми скважинами. Оказывается, что уровень воды из-

меняется с запада на восток, падая почти на 40 м между наблюдениями в скважинах 2 и 3. Если это

падение продолжить, то мы можем ожидать уровни воды выше 142 м в точках западнее наблюдае-

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

мой скв. 3, и уровни ниже 103 м в точках восточнее скв. 2.

Мы можем оценить уровень воды в юго-западном углу карты в точке с координатами X

= 0,

= 0. Сначала используем простой точечный крайгинг и множество из пяти скважин. Это дает

следующую систему весов:





























3895,0

0307,0

7523,0

0110,0

1221,0

Оценим уровень воды (в м):

4,174)148(3895,0)115(0307,0)142(7523,0)103(0110,0)120(1221,0 Y .

Как следовало ожидать, оценка базируется полностью на ближайших скважинах, но нахо-

дится в интервале, определенном наибольшим и наименьшим наблюденными значениями. Оценка

дисперсии ошибки равна s



= 17,3 м

Предполагая дрифт первой степени, получаем коэффициенты универсального крайгинга





























1795,4

7940,1

3832,26

4030,0

1451,0

3133,1

3020,0

5594,0





Используя эти веса, получаем оценку уровня воды (в м):

6,164)148(4030,0)115(1451,0)142(3133,1)103(3020,0)120(5594,0 Y ,

что намного превышает наибольшее контрольное значение. Универсальный крайгинг предназначен

для определения изменения уровня воды или дрифта в пределах локальной окрестности и проекти-

рует его в крайгируемую точку. Оценка дисперсии ошибки равна s



= 26,8 м

, что много больше

чем неопределенность как в оценке дрифта, так и в оценке самой регионализованной переменной.

Вычисление дрифта

Наблюдения, выбираемые для получения оценки крайгинга с некоторой точке р, располага-

ются в зоне влияния вокруг точки р. Крайгинг дает множество весов, которые позволяют прирав-

нять взвешенную сумму полудисперсий между наблюдениями и полудисперсии между наблюде-

ниями и точкой р. Предположим, однако, что все доступные наблюдения вышли за пределы области

влияния. Полувариограммы



iр

между точкой р и некоторым удаленным наблюдением i будут

идентичны для всех наблюдений и равны дисперсии регионализованной переменной (или, при на-

личии дрифта, равны дисперсии остатков от дрифта), т. е. первые n элементов вектора правой части

системы крайгинга будут содержать значения S

, а не значения



iр

. Так как регионализованная пе-

ременная в точке р была статистически независимой от ее значений в каждой из точек наблюдения,

то мы не могли предсказать локальное значение поверхности. Вместо этого оценка, которую мы по-

лучали, решая систему уравнений крайгинга, была основана на глобальных или усредненных свой-

ствах регионализованной переменной. Иными словами, мы оценивали только дрифт.

Мы можем вычислить дрифт в точке р даже в том случае, если используемые наблюдения

расположены в некоторой окрестности, меньшей чем область влияния точки р. Все, что необходимо,

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

– это замена полудисперсий в правой части уравнений крайгинга на полудисперсии, которые на-

блюдались бы в том случае, если бы точка р была расположена так далеко от контрольных точек,

что была бы независимой от них. Так как полудисперсия для всех расстояний вне области влияния

равна дисперсии остатков, то члены в правой части можно приравнять дисперсии остатков, S

. К

сожалению, мы снова зацикливаемся, так как мы не знаем значения S

до тех пор, пока дрифт не

вычислен. К счастью, структурный анализ позволяет нам сделать априорную оценку дрифта, так как

он равен полудисперсии в точке максимума или области влияния.

Следует отметить, что дрифт – это произвольная, но удобная конструкция, необходимая для

того, чтобы удовлетворить требованиям стационарности регионализованной переменной. Может

существовать много различных комбинаций модели дрифта, размера окрестности и оценки полува-

риограммы, которые удовлетворительно представят структуру регионализованной переменной. Вы-

бор некоторой специфической комбинации зависит от степени доступности данных, удобства вы-

числений и других факторов. Продолжим рассмотрение нашего простого примера, предполагая, что

дрифт в данных по уровню воды линеен и что полувариограмма остатков также линейна. Из струк-

турного анализа можно заключить, что область влияния регионализованной переменной распро-

страняется на 30 км. Так как наклон полувариограммы равен 4 м

/км, то дисперсия вне области

влияния должна быть около 4х30 или 120 м

При вычислении дрифта в точке р правая часть матрицы крайгинга имеет следующий вид

 















120

При вычислении крайгинга левая часть [А] остается неизменной, поэтому все, что требуется

для оценки дрифта, – это умножить обратную к [А] матрицу на [С]. Это дает множество из пяти ве-

сов М

, которые используются для вычисления дрифта, плюс три постоянных члена, которые дают

вклад в оценку ошибки дисперсии дрифта. Вектор решения [М] есть

 

















4935,0

9048,0

2283,109

4372,0

1587,0

2202,0

3702,0

1311,0

Дрифт (в м) в точке р находится умножением уровней в наблюдательных скважинах на под-

ходящие коэффициенты дрифта и суммированием:

6,131)148(4372,0)115(1587,0)142(2202,0)103(3702,0)120(1311,0 M .

Ошибка оценки находится как дисперсия умножением слева [С] на транспонированную

матрицу [M]. Например, 3,229



s м

. Как и ранее, стандартная ошибка оценки равна квадратно-

му корню из оценки дисперсии, или 1,153,229 

s м.

Снова предполагая нормальность, можно сделать вероятностные утверждения о доверитель-

ном интервале для истинного значения дрифта. Например, вероятность того, что линейный дрифт

лежит внутри интервала 131,6±30,2 м или между 199,0 и 259,4, равна 95%. (Необходимо напомнить,