Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Подождите немного. Документ загружается.

2/32

035,0070,0

s 



(5.30)

В этой аппроксимации р есть периметр прямоугольной карты. Заметим, что если карта не имеет

краев, как это имело место на торе, то р равно нулю, и эти уравнения тождественны уравнениям

(5.24) и (5.26).

Ожидаемые и наблюденные средние значения расстояний по методу ближайшего соседа мо-

гут быть использованы для построения индекса пространственной схемы. Отношение



/dR 

(5.31)

есть статистика ближайшего соседа и изменяется от 0,0 для распределения, в котором все точки

совпадают и разделены расстояниями, равными нулю, до значения 1,0 для случайного распределе-

ния точек, т. е. до максимального значения 2,15. Последнее значение характеризует распределение,

в котором среднее расстояние до ближайшей окрестности максимизировано. Распределение имеет

форму регулярной шестиугольной схемы, в которой каждая точка равноудалена от шести других

точек. На рис. 5.14 представлены множества точек с различными значениями статистики ближайше-

го соседа, причем все имеют одну и ту же точечную плотность.

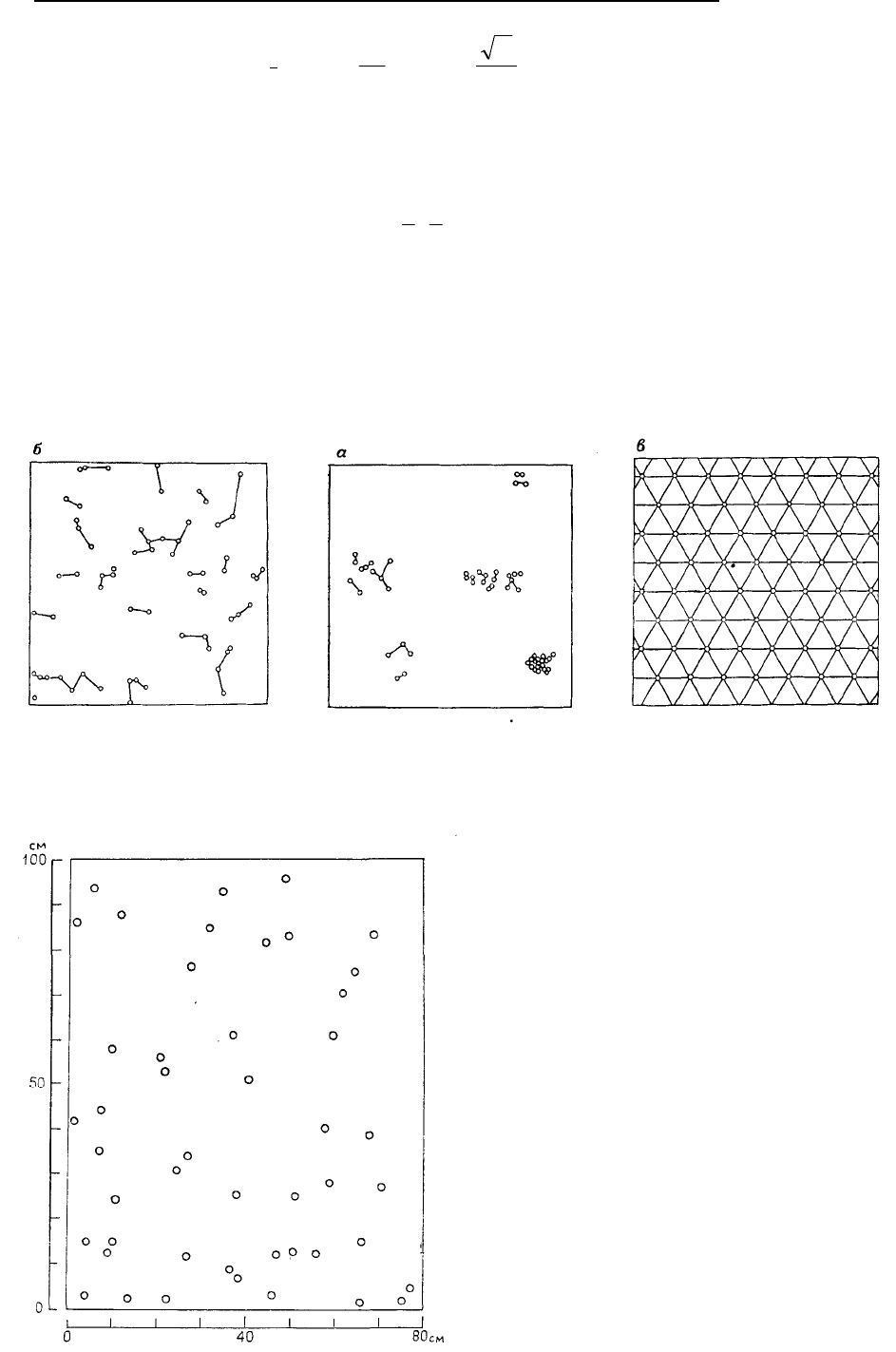
Рис. 5.14. Значения статистик метода ближайшего соседа R для различных схем расположения точек на

картах (по Р. А. Ома, 1984): а – точки сгруппированы в пять групп, R=0,34; б – точки рассеяны случайно,

R=0,91; в – точки размещены по шестиугольной сети, R=2,15. Плотность точек



одинакова для всех схем

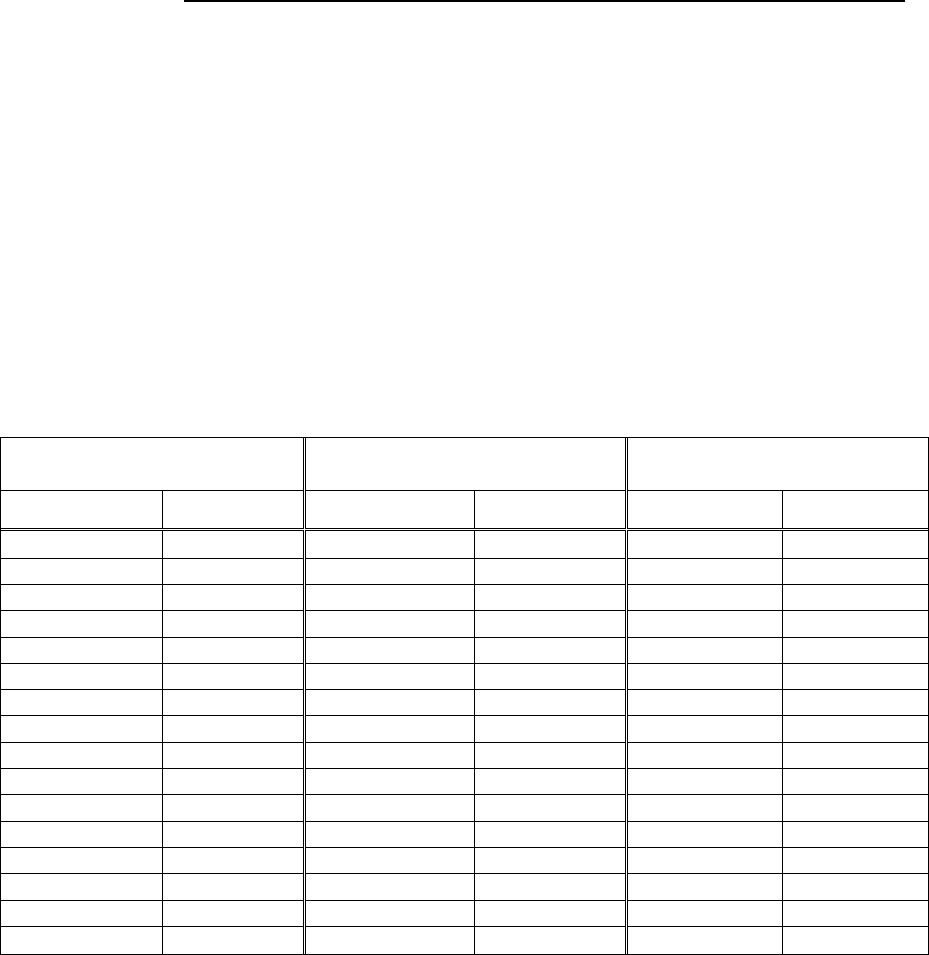
Рис. 5.15. Схематическое представление поли-

рованной плиты анортозита, на которой по-

казано расположение кристаллов магнетита

Проиллюстрируем применение ме-

тода ближайшего соседа, используя «карту»,

изображенную на рис. 5.15. Эта «карта» в

действительности представляет собой поли-

рованную поверхность каменной облицовки

фасада здания банка в университетском го-

родке и служит интересным примером пет-

рологического изучения изверженных по-

род. Это черный анортозит, который содер-

жит мелкие рассеянные кристаллы магнети-

та. Преподаватели нередко используют эти

плиты как наглядное пособие для различной

тематики, включая и применение математи-

ческих методов в петрографии. При этом

обычно постулируется, что положение пли-

ты совпадает с ее природной ориентацией.

Таким образом, рассматривается вертикаль-

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

ная поверхность, нижней части которой соответствует нижний обрез плиты. Так называемая «карта»

характеризует положение всех наблюдаемых на этой поверхности зерен магнетита. В табл. 5.4 при-

ведены значения координат этих точек в сантиметрах, отсчитываемых от левого нижнего угла пли-

ты. В данном случае задача заключается в получении ответа на вопрос: равномерно ли распределе-

ны зерна на поверхности плиты или же они обладают тенденцией к группировке? Кроме того, если

распределение зерен неравномерно, спрашивается, можно ли считать плотность зерен у нижнего

края плиты превышающей плотность у верхнего края. Получение ответа на подобные вопросы игра-

ет существенную роль при решении различных задач петрогенезиса изверженных пород. Рассмат-

риваемые в этой главе методы анализа данных могут оказаться весьма полезными. Проверку гипоте-

зы о равномерном случайном распределении зерен магнетита можно провести с помощью одного из

рассматриваемых ранее способов – разделения на более дробные участки или же с помощью метода

ближайшего соседа. Вычисления можно проделать вручную, измерив расстояния прямо на рис. 5.15,

или вычислив их с помощью координат в табл. 5.4. Риплай [65] (стр. 175 – 181) дает исчерпываю-

щий анализ этих данных, используя различные методы.

Таблица 5.4 Координаты магнетитовых зерен на полированном анортозитовом слое

Расстояние от нижнего левого

угла слоя, см

Расстояние от нижнего левого

угла слоя, см

Расстояние от нижнего левого

угла слоя, см

Горизонтальное

Вертикальное

Горизонтальное

Вертикальное

Горизонтальное Вертикальное

1 86 27 34 50 13

27 12 49 96

РАСПРЕДЕЛЕНИЕ ПРЯМЫХ

Некоторые естественно встречающиеся в природе схемы составлены из линий, таких, как

линеаменты, видимые со спутников, следы трещин на выветренной поверхности гранитов, или мик-

роскопические структуры, наблюдаемые в шлифах деформированной породы. Так же, как множест-

во точек может образовывать схему, которая изменяется от равномерной до кластеризованной с

прочными связями, так и множество прямых может обладать различными свойствами. Конечно, ли-

нии более сложны, чем точки, так как они обладают длиной, ориентацией и местоположением. Со-

ответственно их анализ более труден, и статистические методы, пригодные для изучения множеств

линий, менее развиты, чем методы, предназначенные для исследования схем точек. Изучению рас-

пределения длин линий посвящено мало работ. Исключение составляют работы по логно-

нормальному распределению [2]. Очень небольшое число ученых исследовали распределение про-

странства между линиями в заданной схеме, т. е. решали задачу, аналогичную методу ближайшего

соседа, в анализе точечных распределений [59, 19]. Значительно полнее освещен вопрос об ориента-

ции линий, который будет рассмотрен в следующем параграфе.

Случайную схему линий можно определить как такую схему, в которой каждое положение

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

равновероятно может быть пересечено некоторой линией и любая ориентация секущей линии также

равновероятна. Такие случайные схемы можно генерировать различными способами; одна из таких

процедур состоит в выборе двух пар координат из таблицы случайных чисел и последующем прове-

дении через соответствующие точки прямой. Другой способ состоит в выборе произвольного угла

на плоскости, проведении произвольного радиуса внутри этого угла, проведении на произвольном

расстоянии от вершины угла прямой, перпендикулярной к выбранному радиусу. Повторяя эту про-

цедуру достаточное число раз, получаем в результате схему статистически неразличимых линий.

Мы можем определить меру плотности линий, аналогичную ранее определенной точечной

плотности:







(5.32)

Величина



l – общая длина линий на карте, имеющей площадь A;



– параметр, который

определяет форму пуассоновского распределения; как и следовало ожидать, пуассоновская модель

описывает распределение многих параметров схемы, образованной случайными линиями.

Распределение расстояний между парами линий можно исследовать с помощью метода бли-

жайшего соседа. Сначала произвольно выберем по одной точке на линиях карты. Из каждой точки

по перпендикуляру к ближайшей линии вычисляется расстояние до нее. Среднее этих расстояний до

ближайших соседей

есть среднее этих измерений. Эта процедура проиллюстрирована на рис.

5.16.

Дэси [19] определил среднее расстояние



по методу ближайшего соседа для схемы слу-

чайных линий следующим образом:



/31831,0 (5.33)

а также дисперсию этого среднего:

/10132,0





 (5.34)

Используя эту дисперсию и число линий в схеме, можно найти стандартное отклонение на-

шей оценки среднего расстояния по методу ближайшего соседа. Стандартное отклонение определе-

но формулой





 (5.35)

Она позволяет нам вычислить простую Z-статистику для проверки значимости разности между

ожидаемым и наблюденным средним расстоянием, вычисленным по методу ближайшего соседа:







(5.36)

Критерий является двусторонним. Если величина Z не значима, то можно заключить, что наблю-

денная схема линий неотличима от схемы, порожденной случайным (пуассоновским) распределени-

ем. Мы можем также ввести индекс ближайшего соседа, идентичный тому, который использовался

для точечных схем, взяв отношение наблюденного и ожидаемого среднего расстояний по методу

ближайшего соседа, или



. Индекс интерпретируется совершенно аналогично индексу для то-

чечных схем.

Этот критерий пригоден для множеств как прямых, так и искривленных линий при условии,

что эти линии не часто меняют направление. Значит, линии должны быть по крайней мере в полтора

раза длиннее, чем среднее расстояние между ними. Если число линий на одной карте мало, то оце-

ненную плотность рекомендуется снабдить множителем nn /)1(



, где n – число линий в схеме.

Оценка плотности линий поэтому такова:







)1(



(5.37)

Простой метод исследования множества линий на карте состоит в преобразовании двумер-

ной схемы в одномерную последовательность. Мы можем сделать это, проведя случайно линию на

карте и отмечая точки, в которых эта линия пересекает линии заданного множества. Распределение

интервалов между точками пересечения вдоль проведенной линии дает информацию о пространст-

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

венной схеме. Мы можем применить к исследованию этой одномерной последовательности методы,

изложенные в гл. 4. Если одна секущая не даст достаточного количества пересечений для того, что-

бы можно было применить одномерные критерии, то можно провести некоторую другую случайно

ориентированную линию и т.д. (рис. 5.17). Извилистый путь секущей линии напоминает случайное

блуждание, и последовательность пересечений может рассматриваться как последовательность,

расположенная вдоль одной прямой линии. Этот и другие методы исследования плотности схемы

линий рассмотрены в работе [29].

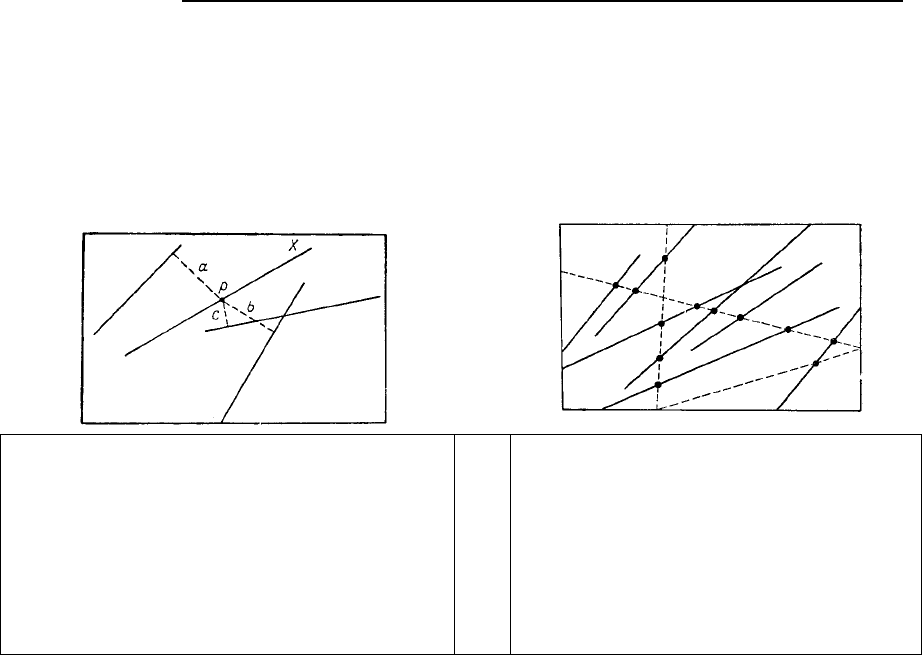
Рис. 5.16. Вычисление расстояний между л

и-

ниями по методу ближайшего соседа. Точка р

выбрана случайно на линии X. Пунктирные линии

а, b и с – это перпендикуляры, проведенные из

точки р к ближайшим линиям. Кратчайшая из них

с – расстояние до ближайшего соседа линии X.

Процесс повторяется с целью нахождения рас-

стояний по методу ближайшего соседа для всех

линий

Рис. 5.17. Случайное расположение линий

опробования (пунктир), секущих схему

линий на карте. Пересечения последними

линий опробования образуют последова-

тельность интервалов, для которых можно

проверить гипотезу о случайности

АНАЛИЗ НАПРАВЛЕННЫХ ДАННЫХ

Направленные данные – важная категория геологической информации. Все объекты, такие,

как плоскости напластований, складчатые поверхности и трещины, характеризуются залеганием,

выраженным простиранием пластов и их наклоном. Ледниковые трещины, маркирующие горизон-

ты, ископаемые раковины и отшлифованная водой галька имеют преобладающие направления ори-

ентации. Фотографии, полученные с воздуха и спутников, также показывают наличие ориентиро-

ванных линейных схем. Указанные объекты могут быть исследованы количественными методами,

наподобие измерений других геологических свойств, однако необходимо использовать специальные

статистики, отражающие циклическую (или сферическую) природу направленных данных.

Учитывая практику географов, мы должны различать направленные и ориентированные

объекты. Предположим, что автомобиль движется на север вдоль шоссе; движение автомобиля име-

ет направление, в то время как шоссе само имеет только ориентацию север – юг. Простирания слоев

пород и прослеживание складок – примеры ориентированных геологических наблюдений, в то вре-

мя как друмлины и некоторые ископаемые, такие, как сильно скрученные гастроподы, имеют ярко

выраженные направленные характеристики.

Мы можем также выделить наблюдения, которые удобно изображать точками на окружно-

сти, или наблюдения, естественно представленные на сфере, например, метаморфические структу-

ры. Первые из упомянутых данных удобно изображать на диаграмме, имеющей форму циклической

гистограммы, вторые – изображаются точками в проекции на полусферу. Хотя геологи многие годы

представляют направленные данные в таком виде, они не разработали формальных статистических

процедур для проверки истинности заключений, которые извлекались из этих диаграмм. Такое по-

ложение достойно сожаления не только потому, что эти критерии полезны сами по себе, но и пото-

му, что развитие многих из этих методов было инспирировано первоначально проблемами наук о

Земле.

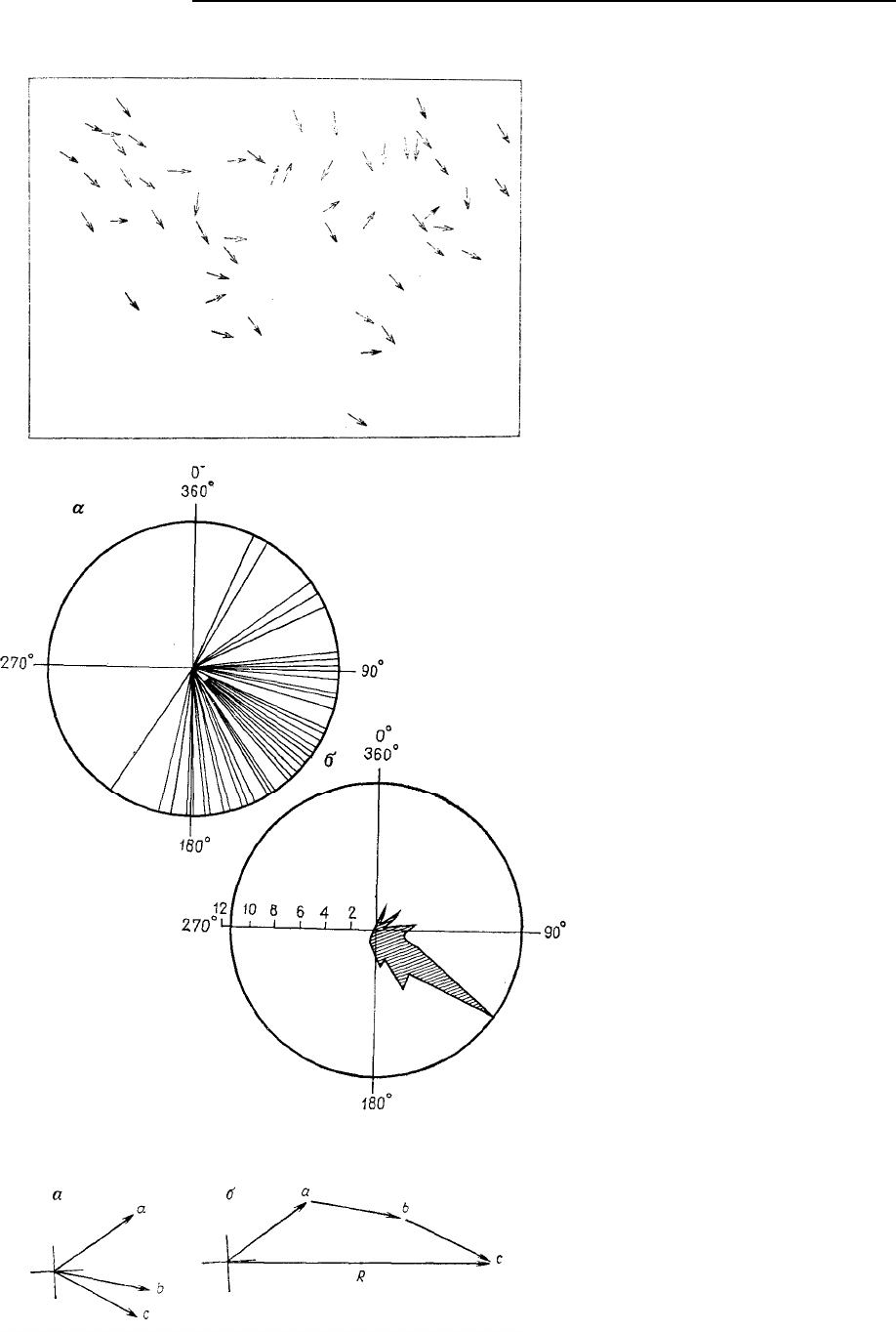
На рис. 5.18 представлена карта трещиноватости ледников, измеренной на малой площади в

Южной Финляндии (табл. 5.5). Направления, указанные штрихами, можно изобразить единичными

векторами или же на окружности единичного радиуса (рис. 5.19, а). Если окружность разбить на

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

сегменты и подсчитать число векторов в каждом сегменте, то результат можно представить в виде

розы или циклической гистограммы (см. рис. 5.19, б). Однако для того, чтобы вычислить статисти-

ки, которые дают характеристики всего множества векторов, мы должны работать непосредственно

с самими измерениями. (Необходимо отметить, что, следуя соглашению между геологами, мы изме-

ряем углы против часовой стрелки от положительного направления оси Y, т.е. от направления на

север). В большинстве работ по статистике направленных данных углы измеряются против часовой

стрелки от положительного направления оси X, т.е. направления на восток.

Таблица 5.5. Вектор направлений штриховки ледника, измеренный на

площади в Южной Финляндии (значения даны в градусах, отсчет вел-

ся против часовой стрелки, начиная с севера)

125

132

146

172

100

126

132

153

179

105

126

132

155

181

113

126

134

155

186

113

127

135

155

190

114

127

137

157

212

117

128

144

163

121

128

145

165

123

129

145

171

Главное направление в некотором множестве векторов можно найти, вычисляя результи-

рующий вектор – результант. Пусть Х и Y – координаты конца единичного вектора, направление

которого задается углом 9:



cos ,



sin (5.38)

Такие три вектора представлены на рис. 5.20. Также показан результирующий вектор, полу-

ченный суммированием синусов и косинусов индивидуальных векторов:





cos







sin



(5.39)

Из результирующего вектора можно получить среднее направление



, которое является уг-

ловым средним всех векторов выборки. Оно совершенно аналогично среднему значению множества

скалярных измерений:

 

 





iirr

1 1

)cos/sin(tan)/(tan



(5.40)

Очевидно, величина или длина результирующего вектора зависит отчасти от вклада диспер-

сии выборки векторов, но также и от числа векторов. Для сравнения результирующих векторов вы-

борок различного объема их необходимо привести к стандартному виду путем деления координат

результирующего вектора на число наблюдений:







cos









sin



(5.41)

Заметим, что эти координаты также определяют центроид конечных точек заданных единичных

векторов.

Результирующий вектор дает информацию не только о среднем направлении некоторого

множества векторов, но и о расположении векторов относительно среднего. На рис. 5.21,а представ-

лены три вектора, которые только немного отклоняются от среднего направления. Результирующий

вектор по длине почти равен сумме длин трех этих векторов. Наоборот, три вектора, представлен-

ные на рис. 5.21, б, сильно разбросаны; их результирующий вектор очень короткий. Длина резуль-

тирующего вектора, обозначаемая R, определена по теореме Пифагора:







irr

YXR

)sin()cos(



(5.42)

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Рис. 5.18. Карта, представляющая на-

правления штриховки ледника в юж-

ной части Финляндии (51 измерение)

на площади 35 км

Рис. 5.19. Направления штрихов-

ки ледника, изображенные на рис.

5.18: а – направления, представлен-

ные как единичные векторы; б –

направления, представленные как

роза-диаграмма, на которой указаны

числа векторов внутри последова-

тельных 10-градусных интервалов

Рис. 5.20. Определение среднего направ-

ления множества единичных векторов: а

– три вектора, взятые с рис. 5.18; б – вектор

R, полученный комбинированием трех

единичных векторов. Порядок комбиниро-

вания несуществен.

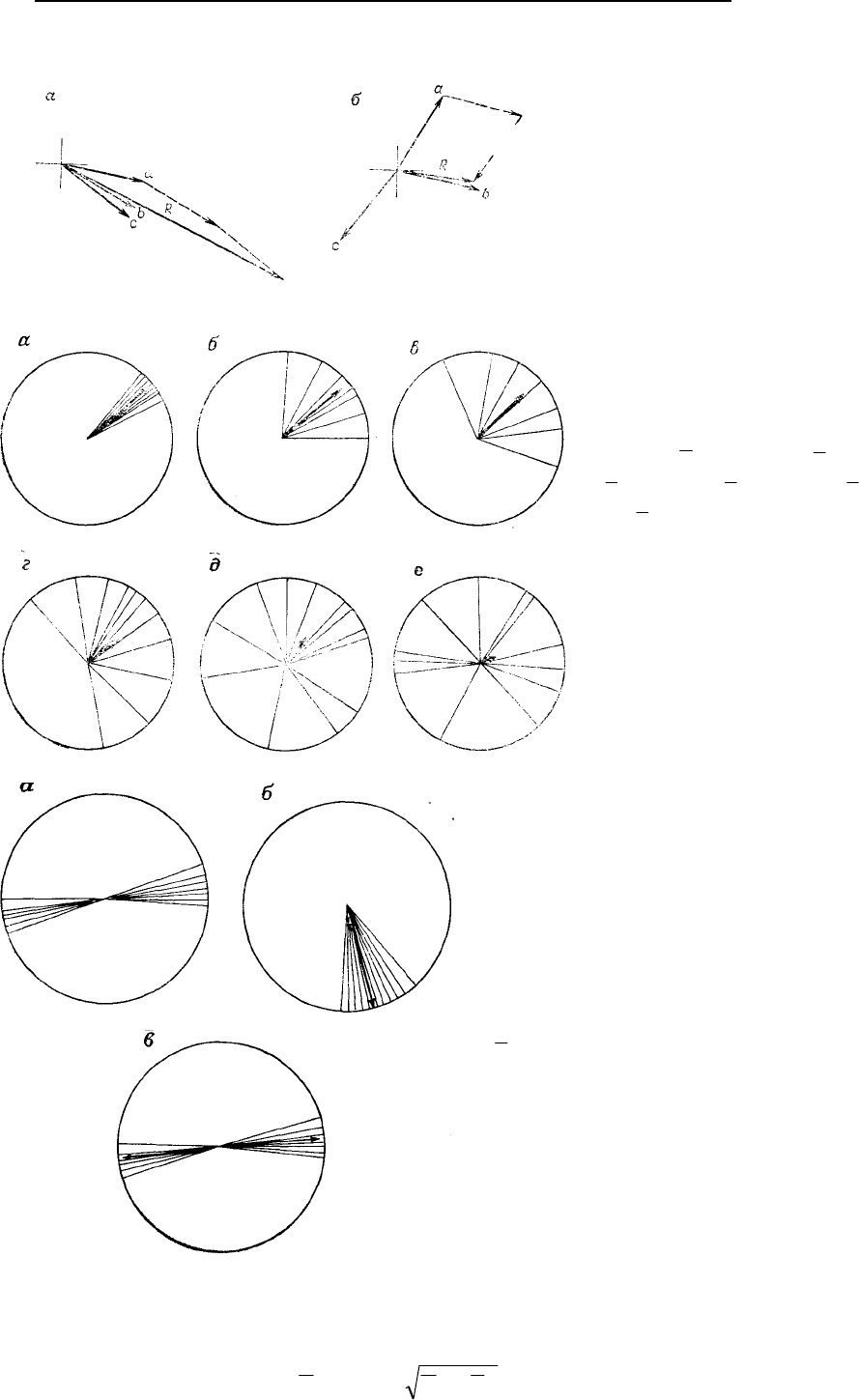
Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Рис. 5.21. Использование длины

вектора R для выражения диспер-

сии некоторого набора единичных

векторов: а – три вектора, располо-

женных в узком пучке вокруг общего

направления; вектор R относительно

длинный, близкий к числу n; б – три

широко рассеянных вектора; R имеет

длину, меньшую единицы

Рис. 5.22. Множества единичных

векторов, иллюстрирующие значе-

ние, получаемое при различном

расположении векторов во всех

примерах, среднее направление –

52°: a –

997,0R

; б –

90,0R

; в –

75,0R

; г –

55,0R

; д –

40,0R

;

е –

10,0R

Рис. 5.23. Удвоение угла с целью вычисления

средней ориентации: а – ориентация измерении,

представленных как векторные направления; ре-

зультант R среднего направления равен 285° и

близок к нулевому по длине (R=0,08); б – ориента-

ция измерений, представленных как векторы на-

правлений после удвоения углов. Распределение

более не является бимодальным; вектор R отража-

ет правильный тренд удвоенных углов и близок к

единице по длине (среднее направление – 120°;

97,0R

); в – ориентации вновь нанесены как ис-

ходные углы и истинное направление вектора R

(81°) находится делением пополам направления R

в «б»

Длину результирующего вектора можно стандартизировать делением на число наблюдений.

Стандартизованный результирующий вектор по длине равен также квадратному корню из суммы

квадратов стандартизованных координат концевых точек:

/ SCnRR  (5.43)

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Величина

называется средней длиной результирующего вектора и изменяется от нуля до

единицы. Эта мера аналогична дисперсии, но в некотором смысле противоположна ей. Большие

значения

указывают на то, что наблюденные векторы находятся в узком пучке с малой дисперси-

ей, а значения

, близкие к нулю, указывают на большой разброс векторов. На рис. 5.22 представ-

лены множества векторов, имеющих различные значения

. Для того, чтобы иметь меру диспер-

сии, которая увеличивается с увеличением рассеяния, R иногда заменяют на его дополнение, назы-

ваемое циклической дисперсией:

nRnRs /)(1

 (5.44)

Можно вычислить и другие направленные статистики, включая циклические аналоги стан-

дартного отклонения, моды, медианы. Их определения приведены в удобной таблице Гейлом и Бер-

том [28].

Ориентация данных может быть изменена до вычисления средних направлений или мер рас-

сеяния. Так как ориентация может иметь одно из двух противоположных значений, то во избежание

ошибок в определении дисперсии необходимо принять некоторые соглашения. На примере ориен-

тации речной гальки Крамбейн [47] предлагает новое решение этой задачи. Если все измеренные

углы удвоить, будет записан тот же угол, независимо от того, какая ориентация была использована.

В качестве примера рассмотрим шарнир складки, которая простирается с северо-востока на юго-

запад. Его ориентация будет одинаковой независимо от того, задать ли угол равным 45° или 225°.

Если удвоить углы, мы получим

оо

90245 

оо

4502225 

, что составляет

ооо

90360450 

Среднее направление, длина среднего результирующего вектора и циклическая дисперсия

могут быть найдены обычным образом после того, как ориентированные утлы были удвоены. Для

нахождения истинной средней ориентации разделим вычисленный угол среднего направления на

два. Это проиллюстрировано на рис. 5.23.

Проверка гипотез о циклически распределенных данных

Для проверки статистических гипотез о циклически распределенных данных мы должны

иметь некоторую вероятностную модель, соответствующую изучаемому параметру. Существуют

циклические аналоги одномерных распределений, которые мы обсудили в гл. 2, однако наиболее по-

лезно из них распределение фон Мизеса. Это – циклический эквивалент нормального распределения,

также обладающий двумя параметрами: средним направлением



и параметром концентрации k.

Распределение фон Мизеса унимодально и симметрично относительно среднего направления. По ме-

ре увеличения параметра концентрации вероятность получения направленного измерения, очень

близкого к среднему направлению, увеличивается. Если к равно нулю, все направления равновероят-

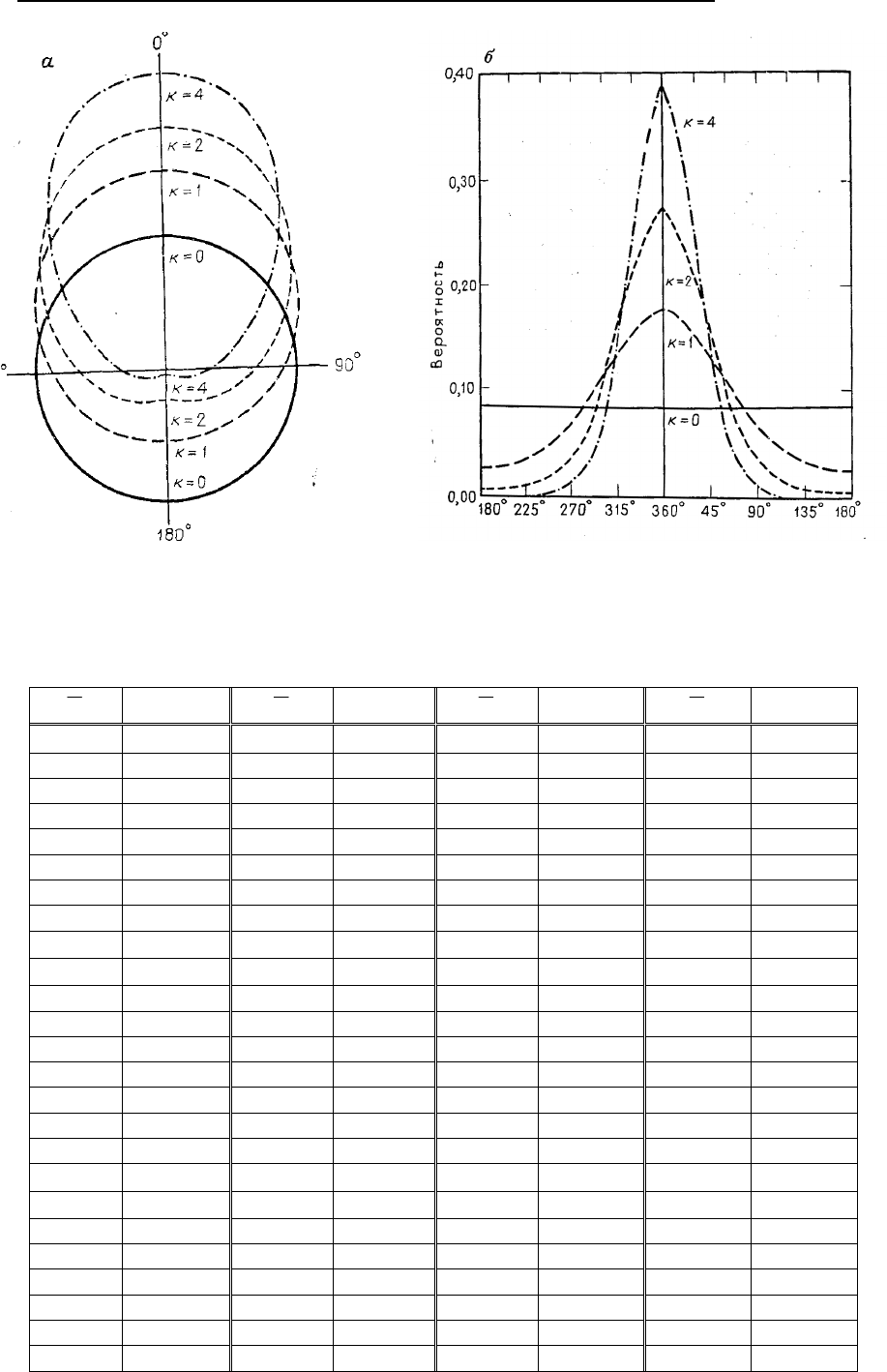
ны и распределение становится циклическим равномерным. На рис. 5.24, а представлена форма рас-

пределения фон Мизеса для некоторых значений k. Это распределение может быть также представ-

лено в условной форме (рис. 5.24, 6).

Прямое определение параметру концентрации затруднительно, но его можно оценить через

, если допустить, что данные являются выборкой из совокупности, имеющей распределение фон

Мизеса. В табл. 5.6 приведены оценки максимального правдоподобия для параметра k, соответст-

вующие некоторому вычисленному

. В некоторых приводимых ниже статистических критериях

мы будем использовать эти оценки параметра k.

Критерии проверки случайности.

Простейшая гипотеза, которую можно проверить статистическими методами, это гипотеза о

случайности направленных наблюдений. Это эквивалентно утверждению о том, что нет предпочти-

тельных направлений или же что вероятность любого направления одинакова. Если предположить,

что наблюдения представляют выборку из совокупности с распределением фон Мизеса, то соответ-

ствующая гипотеза эквивалентна утверждению, что параметр концентрации к равен нулю, так как

при k=0 распределение циклически равномерно. Иными словами, нулевая гипотеза и альтернатива

таковы: H

:k=0, H

:k>0.

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Рис. 5.24. Распределения фон Мизеса, имеющие различные параметры концентрации [33]:

a – распределение, представленное в полярной форме; б – распределение, представленное как ус-

ловное. Интервал измерения соответствует полной окружности

Таблица 5.6. Оценка максимума правдоподобия параметра концентрации k для вычислен-

ных значении R [5, 33]

0,00 0,00000

0,25

0,51649

0,50

1,15932

0,75

2,36930

0,01

0,02000

0,26

0,53863

0,51

1,19105

0,76

2,45490

0,02

0,04001

0,27

0,56097

0,52

1,22350

0,77

2,54686

0,03

0,06003

0,58350

0,53

1,25672

0,78

2,64613

0,04

0,08006

0,29

0,60625

0,54

1,29077

0,79

2,75382

0,05

0,10013

0,30

0,62922

0,55

1,32570

0,80

2,87129

0,06

0,12022

0,31

0,65242

0,56

1,36156

0,81

3,00020

0,07

0,14034

0,32

0,67587

0,57

1,39842

0,82

3,14262

0,08

,16051

0,33 0,69958

0,58

1,43635

0,83

3,30114

0,09

0,18073

0,34 0,72356

0,59

1,47543

0,84

3,47901

0,10

0,20101

0,35

0,74783

0,60

1,51574

0,85

3,68041

0,11

0,22134

0,36

0,77241

0,61

1,55738

0,86

3,91072

0,12

0,24175

0,37

0,79730

0,62

1,60044

0,87

4,1770

0,13

0,26223

0,38

0,82253

0,63

1,64506

0,88

4,48876

0,14

0,28279

0,39

0,84812

0,64

1,69134

0,89

4,85871

0,15

0,30344

0,40

0,87408

0,65

1,73945

0,90

5,3047

0,16

0,32419

0,41

0,90043

0,66

1,78953

0,91

5,8522

0,17

0,34503

0,42

0,92720

0,67 1,84177

0,92

6,5394

0,18

0,36599

0,43

0,95440

0,68 1,89637

0,93

7,4257

0,19

0,38707

0,44

0,98207

0,69

1,95357

0,94

8,6104

0,20

0,40828

0,45

1,01022

0,70

2,01363

0,95

10,2716

0,21

0,42692

0,46

1,03889

0,71

2,07685

0,96

12,7661

0,22

0,45110

0,47

1,06810

0,72

2,1435

0,97

16,9266

0,23

0,47273

0,48

1,09788

0,73

2,21425

0,98

25,2522

0,24

0,49453

0,49

1,12828

0,74

2,28930

0,99

50,2421

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Критерий крайне прост и требует лишь вычисления значения

по формуле (5.43). Затем

эта статистика сравнивается с критическим значением

для заданного уровня значимости. Если

наблюдения извлечены из циклического равномерного распределения, то можно ожидать, что

будет мало (см. рис. 5.22, е). Однако если вычисленная статистика превышает критическое значе-

ние, то нулевая гипотеза должна быть отклонена, и можно предположить, что наблюдения получены

из совокупности, имеющей предпочтительную ориентацию. Этот критерий был получен лордом Ре-

леем в начале столетия; современное изложение соответствующих вопросов принадлежит Мардиа

[51]. В табл. 5.7 приведены критические значения

для различных объемов выборки и уровней

значимости.

Таблица 5.7. Критическое значение

критерия Релея о наличии

предпочтительного тренда [51]

Число

наблюдений n

Уровень значимости



, %

10 5 2,5 1

0,768

847

0,905

0,960

0,677

0,754

0,816

0,879

0,618

0,690

0,753

0,825

0,572

0,642

0,702

0,771

0,535

0,602

0,660

0,725

0,504

0,569

0,624

0,687

0,478

0,540

0,594

0,655

0,456

0,516

0,567

0,627

0,437

0,494

0,544

0,602

0,420

0,475

0,524

0,580

0,405

0,458

0,505

0,560

0,391

0,443

0,489

0,542

0,379

0,429

0,474

0,525

0,367

0,417

0,460

0,510

0,357

0,405

0,447

0,496

0,348

0,394

0,436

0,484

0,339

0,385

0,425

0,472

0,331

0,375

0,415

0,461

0,323

0,367

0,405

0,4

0,316

0,359

0,397

0,441

0,309

0,351

0,389

0,432

0,303

0,344

0,381

0,423

0,277

0,315

0,348

0,387

0,256

0,292

0,323

0,359

0,240

0,273

0,302

0,336

0,226

0,267

0,285

0,318

50 0,124 0,244 0,270 0,301

Напомним, что критерий Релея основан на предположении, что наблюденные векторы из-

влечены из совокупности с распределением фон Мизеса, т.е. совокупность векторов либо имеет

равномерное распределение, если k=0, либо имеет единственную моду или предпочтительное на-

правление. Если же в действительности векторы извлечены из бимодального распределения, такого,

например, как изображено на рис. 5.23, то этот критерий дает ошибочные результаты.

Проверим, не имеют ли предпочтительного направления штриховки ледника в Финляндии

при уровне значимости 5%. Так как имеется 50 наблюдений, то табл. 5.7 дает критическое значение

244,0

05,0;50

R . Проверяемая статистика – это просто нормализованное значение

. Сумма коси-

нусов векторов равна Х

= –25,793 и сумма синусов равна Y

=31,637. Длина есть

819,40)637,31()793,25(

R