Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

Подождите немного. Документ загружается.

211

Продолжение табл. 6.39. Матрица сходства, собственные значения и два первых соб-

ственных вектора, вычисленных для данных по случайным блокам; перечислены

факторные нагрузки R- и Q-метода соответствия на первые два фактора

Вектор

Собственные

значения

Общее сходство

(%)

Общее сходство

(кумулятивные %)

1 0,1213 70,8332 70,8332

0,0359

20,9437

91,7769

0,0110

6,4431

98,2201

0,0029

1,6891

99,9091

0,0001

0,0837

99,9928

0,0000

0,0072

100,0000

7 0,0000 0,0000 100,0000

Собственный вектор

Переменная

I II

0,1922 –0,0538

0,2783

–

0,2

148

0,4961

0,4085

0,3109

–

0,0447

–

0,4126

–

0,1458

–

0,4710

–

0,2967

–0,3883 0,8203

Нагрузки, на оси в методе соответствия

R-метод Q-метод

Переменная I II Блок I II

0,1555 –0,0237

а –0,5814

0,0088

0,2747

–

0,1153

–

0,1290

–

0,1257

0,6980

0,3126

0,4855

0,0899

0,2219

–

0,0173

0,6570

0,1459

–

0,3809

–

0,0732

0,1998

–

0,0955

–

0,3793

–

0,1299

–

0,1507

–

0,0214

–0,5467 0,6280 g –0,8040

0,5665

h 0,3164

–0,0467

–

0,2322

–

0,2435

–

0,3215

–

0,0086

–

0,2

154

–

0,0698

0,3782

0,0457

0,1067

0,1565

–

0,2370

0,2185

–

0,2046

0,7453

–

0,0421

–

0,0861

–

0,0520

–

0,2084

0,1873

–

0,0313

–

0,2654

–

0,0455

–

0,0217

0,0662

–

0,2393

–

0,2097

0,4181

0,0395

0,5015

0,2009

0,1477

0,0399

0,5008

0,0539

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

212

Таблица 6.40. Данные по блокам: каждая исходная переменная представлена тремя группами (L –

низкие, М – средние, Н – высокие значения); в результате получается матрица исходных данных

порядка 2125

Блок

321

NML

321

NML

321

NML

321

NML

321

NML

321

NML

321

NML

1 0 0

0 1 0

1 0 0

0 0 1

1 0

0 0 1

0 1 0

1 0 0

0 0 1

0 1 0

1 0 0

0 1 0

0 0 1

0 1 0

1 0 0

0 1 0

0 0 1

0 1 0

0 0 1

1 0 0

0 0 1

0 1 0

0 0 1

1 0 0

0 1 0

1 0 0

0 1 0

1 0 0

0 1 0

1 0

1 0 0

0 1 0

0 0 1

0 1 0

0 0 1

1 0 0

0 0 1

1 0 0

0 1

0 0 1

1 0 0

0 0 1

1 0 0

0 1 0

0 0 1

0 1 0

0 0 1

1 0 0

0 1 0

1 0 0

1 0

0 1 0

1 0 0

0 1 0

1 0 0

0 1 0

1 0 0

0 1 0

1 0 0

0 1 0

1 0 0

0 1 0

1 0 0

0 0

0 0 1

1 0 0

0 0 1

1 0 0

0 0 1

0 1 0

0 0 1

1 0 0

0 1 0

1 0 0

0 1 0

1 0

0 1 0

1 0 0

0 1 0

1 0 0

0 1 0

1 0 0

0 0 1

1 0 0

0 0 1

1 0 0

0 0 1

1 0

0 1 0

0 0 1

1 0 0

0 1 0

1 0 0

0 1 0

1 0 0

0 1 0

1 0 0

0 0 1

1 0 0

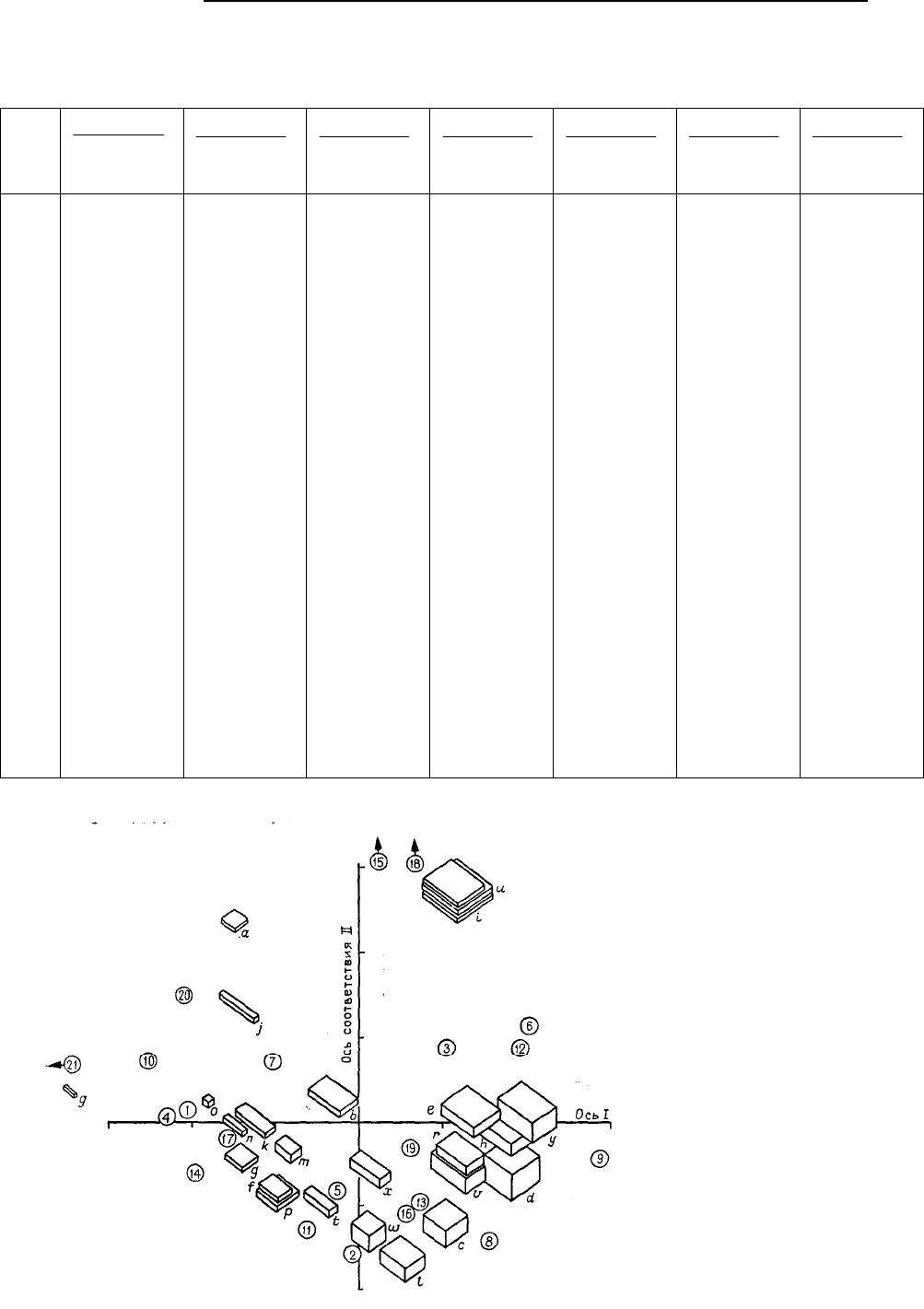
Рис. 6.47. Представление

нагрузок R- и Q-методов на

первые две оси соответст-

вия для данных по блокам в

порядке возрастания их

объемов. Цифры в кружках –

нагрузки R-метода (см. табл.

6.40. Значения 15, 18 и 21 –

вне области диаграммы)

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

213

Рис. 6.46. Представление нагрузок R- и Q-методов анализа соответствия на

первые две оси для данных по блокам

СОВМЕСТНЫЙ R- И Q-ФАКТОРНЫЙ АНАЛИЗ

Хотя теорема Эккарта–Юнга утверждает, что R- и Q-методы дают эквивалентные решения,

на практике это не всегда так. Достаточно взглянуть на рис. 6.38 и 6.39, чтобы убедиться в том, что

факторные метки R-метода выглядят иначе, чем факторные нагрузки Q-метода. Напомним, что ре-

шение R-метода получается из симметричной матрицы-произведения [W]'[W], имеющей меньший

порядок, в то время как решение Q-метода получается из произведения матриц [W][W]', имеющего

больший порядок. К сожалению, шкалирование, используемое для получения матрицы [W] из мат-

рицы необработанных данных [X], не одинаково в этих двух методах. Например, глазные компонен-

ты содержат преобразование каждого элемента матрицы [X], состоящее в делении на стандартное

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

214

отклонение столбцов, что приводит к шкалированной матрице данных [W]. Q-метод факторного

анализа использует стандартизацию, состоящую в делении каждого элемента [X] на квадратный ко-

рень из суммы квадратов строк, что приводит к шкалированной матрице [W]. Однако матрица [W] в

анализе главных компонент не идентична матрице [W], полученной на первом шаге Q-метода фак-

торного анализа. Различие в шкалировании ухудшает решение в одном методе по отношению к дру-

гому.

Имеется несколько подходов к этой задаче. Очевидно, если не проводится никакого шкали-

рования, то собственные векторы и собственные значения для [X]'[X] такие же, как и для [X][X]',

исключая лишь то различие, что одна из этих матриц имеет дополнительные нулевые собственные

значения. Факторные метки R-метода будут пропорциональны нагрузкам Q-метода, и наоборот.

Кроме того, R- и Q-факторные нагрузки располагаются в том же пространстве, что и факторные

оси, поэтому их можно нанести на одну и ту же диаграмму, как это представлено на рис. 6.48.

К сожалению, использование необработанной матрицы непарных произведений имеет

большие неудобства. Так как при этом не проводится никакого шкалирования, то результаты анали-

за очень чувствительны к выбору единиц измерения и могут просто отражать средние величины пе-

ременных, а не свойства дисперсий и ковариаций. Хотя, по-видимому, такой метод – наиболее про-

стой способ получения факторов R- и Q-методов. он почти никогда не используется на практике.

Второй подход состоит в шкалирова-

нии матрицы [X] так, чтобы строки и столбцы

можно было трактовать одинаковым образом.

В анализе соответствия это делается путем де-

ления каждого элемента на произведение квад-

ратных корней из сумм по строкам и столбцам.

Хотя этот метод очень чувствителен, его не-

достатки менее заметны, если мы имеем дело с

условными таблицами и если применяем его к

результатам измерений.

Третий подход – это поиск способа та-

кого шкалирования строк, который дал бы со-

держательную меру взаимных связей между

строками матрицы [W], и в то же время полу-

чалась бы содержательная мера взаимосвязей

между столбцами. Эта задача оказывается не

столь сложной, как кажется на первый взгляд,

и это является базисом по меньшей мере двух

практических методов одновременного нахож-

дения факторов R- и Q-методов.

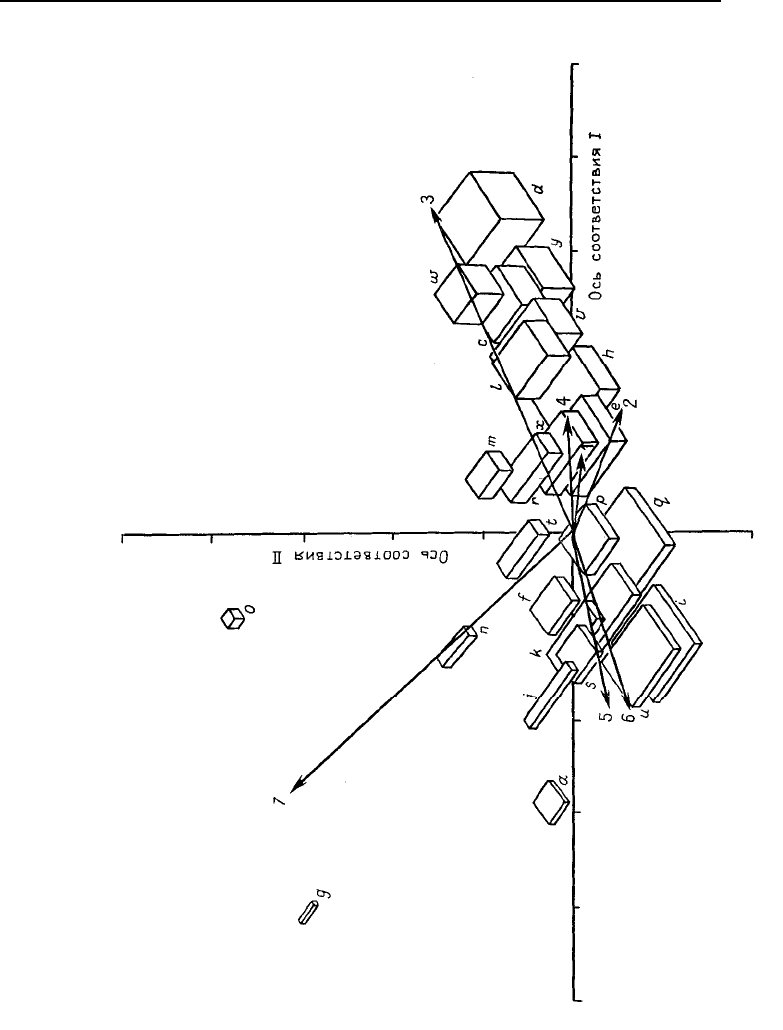
Рис. 6.48. Представление нагрузок R- и Q-

методов на две первые факторныеоси для дан-

ных по блокам, вычисленных для матрицы не-

обработанных сумм квадратов и попарных про-

изведений [X]'[X]. Блоки представлены как объек-

ты, характеризуемые нагрузками Q-метода; пере-

менные – как векторы, определенные нагрузкам R-

метода. Конец оси Х

находится за пределами диа-

граммы в направлении оси X

; конец оси Х

– за

пределами диаграммы в направлении оси X

Элементы матрицы [X] стандартизуются с помощью вычитания средних столбца (перемен-

ной) и деления на квадратный корень из п числа наблюдений, т.е.

nxxw

ijij

)(  (6.93)

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

215

Тогда меньшая матрица-произведение [W]'[W] будет содержать дисперсии и ковариации перемен-

ных. В то же время большая матрица-произведение [W][W]' эквивалентна матрице главных коорди-

нат Q, когда сходство между объектами определяется евклидовым расстоянием, т.е.

)(

ijij

ddddq



 (6.94),

и d

– элемент матрицы расстояний [D]:







jkikij

nxxd

)( (6.95)

С другой стороны, можно стандартизовать элементы матрицы: [X], вычитая среднее по столбцу (пе-

ременной) и выполняя деление на произведение стандартных отклонений и квадратного, корня из n:







(6.96)

Меньшая матрица-произведение [W]'[W] будет теперь содержать дисперсии и ковариации перемен-

ных в стандартизованной форме, которые есть не что иное как коэффициенты корреляции между

переменными.

Снова большая матрица-произведение [W][W]' эквивалентна одной из версий матрицы глав-

ных координат [Q]. Теперь, однако, матрица расстояний [D] содержит евклидовы расстояния между

наблюдениями, как определено стандартизованными переменными, или





















jkik

(6.97)

Чтобы осуществить совместный R- и Q-факторный анализ, мы сначала вычислим меньшую

матрицу-произведение [W]'[W] после шкалирования по формулам (6.93) или (6.96). Затем вычислим

собственные векторы и собственные значения, а также R-факторные нагрузки, умножая каждый

элемент собственного вектора на соответствующее сингулярное значение или квадратный корень из

его собственного значения. Если матрицу собственных векторов обозначить через [U], то будем

иметь

][][][  UA

(6.98)

где снова  – диагональная матрица сингулярных значений [W]'[W]. Далее вычислим Q-факторные

нагрузки, которые находятся как произведение шкалированной матрицы данных на матрицы собст-

венных векторов:

][][][ UWA

 (6.99)

Конечно, можно также найти факторные метки, R-факторные метки находятся умножением шкали-

рованной матрицы данных на матрицу R-факторных нагрузок:

][][][

AWS  (6.100)

Q-факторные нагрузки находятся по формуле

]][[][][][][ UWWAWS







 (6.101)

Так как R-факторные нагрузки [A

] дают координаты переменных как точки факторного

пространства и Q-факторные нагрузки [A

] дают координаты объектов как точки того же факторно-

го пространства, то обе совокупности факторных нагрузок можно нанести на одни и те же фактор-

ные диаграммы. Переменные, которые нанесены близко друг к другу, очень похожи. Теорема Эк-

карта–Юнга дает соотношение между переменными и объектами. Уравнение (6.40) может быть пе-

реписано в виде

][][]][[

WAA









(6.102)

Элемент матрицы [W], таким образом, равен





waa



(6.103)

Значение w

, которое является шкалированным значением переменной j, наблюдаемой на объекте i,

можно рассматривать как произведение вектора нагрузок объекта [a

] и вектора нагрузок перемен-

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

216

ной [a

], умноженного на



1 . Величина векторного произведения, как указывалось в гл. 5 (см.

гл. 5), обратным образом связана с расстоянием между концами двух векторов. Таким образом, сила

связи между объектом и переменной в факторной диаграмме прямо выражается как расстояние ме-

жду точкой объекта и переменной точкой.

Хотя между факторными метками существуют эквивалентные соотношения, все же они не

очень хорошо выражаются в терминах сходства. Наилучший способ изображения результатов одно-

временного R- и Q-факторного

анализа – это представление

двух множеств факторных на-

грузок в проекции на фактор-

ные оси. Это сделано для дан-

ных по случайным блокам на

рис. 6.49. Как для R-метода, так

и для метода главных компо-

нент, критические матрицы бу-

дут одинаковыми (см. табл.

6.21).

Двойственность между

анализом главных компонент и

анализом главных координат,

основанном на использовании

евклидова расстояния, была

впервые указана Говером [20].

Однако эта двойственность до

недавнего времени не исполь-

зовалась, хотя множество про-

грамм факторного анализа ис-

пользует сингулярное разложе-

ние матриц, которое является

следствием теоремы Эккарта–

Юнга.

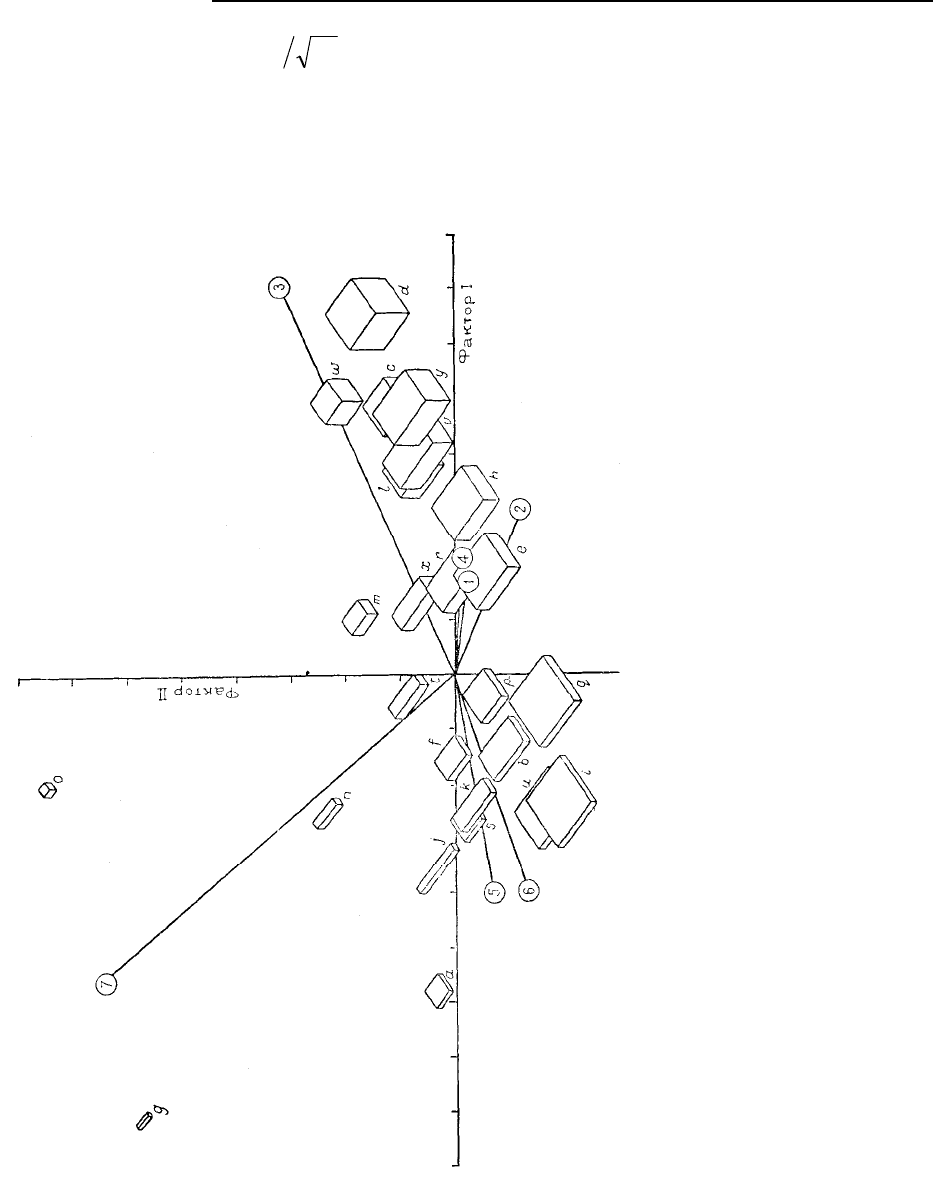
Рис. 6.49. Представление нагру-

зок R- и Q-методов на первые

две факторные оси для данных

по блокам, вычисленных из мат-

рицы дисперсии и ковариации

[W]'[W]. Блоки представлены как

объекты, соответствующие нагруз-

кам Q-метода. Переменные пред-

ставлены векторами, характери-

зующимися нагрузками R-метода

Математическое обоснование одновременного R- и Q-факторного анализа дано Зу, Чангом и

Девисом [66], которые также приводят большое число примеров его использования в геологии.

В табл. 6.41 содержатся измерения, сделанные по профилю через небольшой высокорадио-

актизный кварц-монцонитовый плутон, интрудированный в хлорит-актинолитовый сланец вблизи

Береа, штат Виргиния. По этому профилю анализировались на содержание радиоактивных урана,

тория и калия 22 образца из буровых скважин. В тех же местах вдоль профиля были сделаны воз-

душные радиометрические измерения. Цель исследования, первоначально проведенного Шерманом,

Банкером и Вашем [57], состояла в установлении связи между содержаниями радиоактивных эле-

ментов и радиометрическими измерениями.

Данные были проанализированы Зу, Чангом и Девисом [66] с использованием шкалирования

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

217

по формуле (6.96). В табл. 6.42 приведены матрица коэффициентов корреляции, собственные значе-

ния, R- и Q-факторные нагрузки. На рис. 6.50 представлены R- и Q-факторные нагрузки на первые

две оси в факторном пространстве. Очевидно различие между пробами, взятыми из плутона, и про-

бами, собранными в сланцах материнской породы и аллювиального покрытия.

Таблица 6.41. Содержания урана, тория и калия и интенсивность результатов

воздушной радиометрической разведки (ВР), проведенной вдоль разреза ин-

трузии кварцевых монцонитов вблизи Берея, штат Виргиния [57]

Номер ВР* U, г/т Th, г/т К, %

1 240 0,63 2,05 0,13

360

2,18

5,31

0,31

420

2,26

5,61

0,34

500

1,71

6,44

0,70

580

2,38

7,99

1,73

700

3,83

8,32

4,26

600

3,79

9,46

1,53

650

4,09

14,71

3,11

770

4,21

12,00

1,90

930

4,72

12,78

2,92

1020

6,24

16,31

2,29

1000

5,24

14,51

1,88

1000

4,73

15,79f

4,64

1040

4,67

10,30

4,17

1150

5,08

13,11

3,97

1000

5,27

13,40

4,36

960

5,61

10,31

2,05

420

2,33

6,83

0,47

370

2,64

,88

0,58

400

2,29

6,02

0,34

480

2.32

6,14

0,32

22 730 5,94 12,86 1,35

* Воздушные радиометрические измерения в расчете на 1 с.

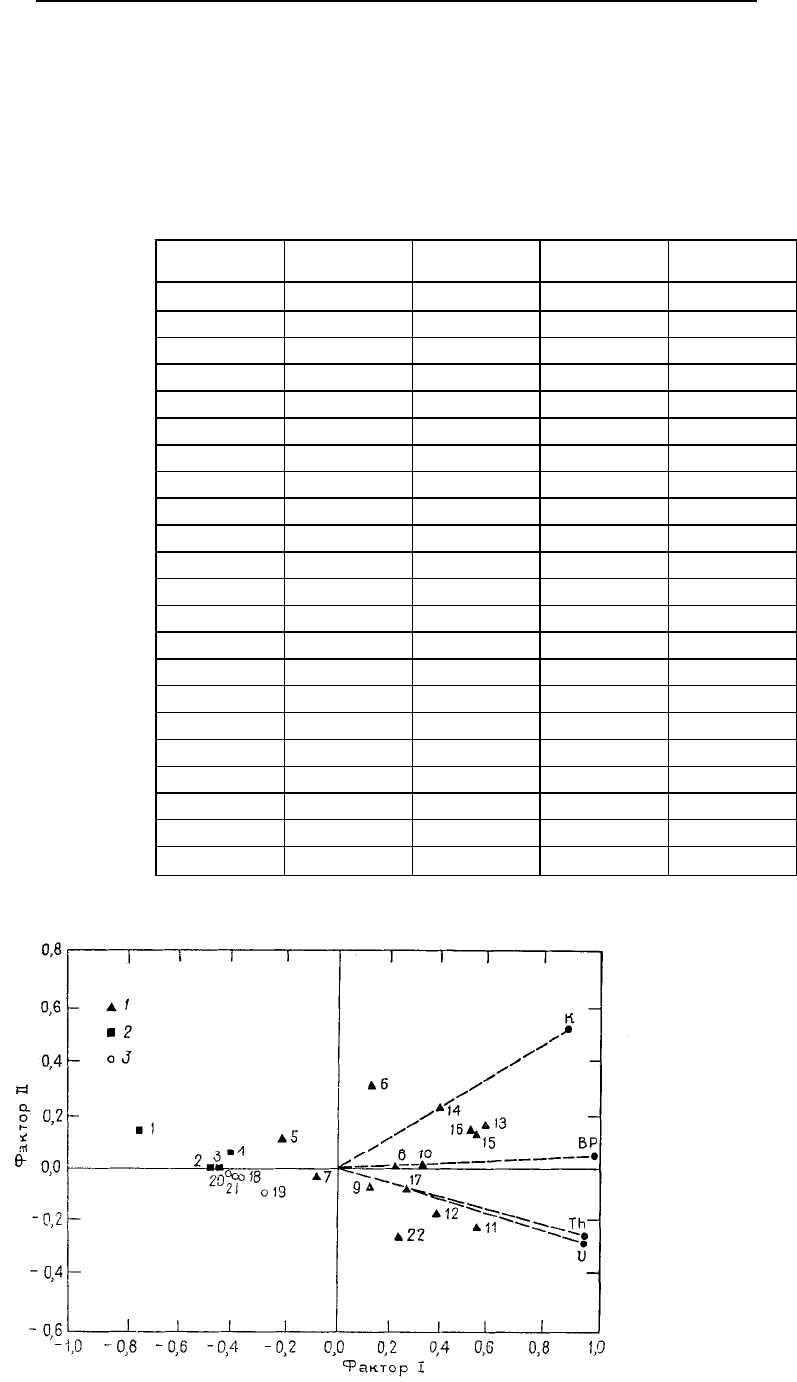
Рис. 6.50. Представление нагру-

зок R- и Q-методов на две пер-

вые факторные оси для данных

Береа, вычисленных из кова-

риационной матрицы (см. табл.

6.42) [65]. Пунктирные линии –

нагрузки R-метода; 1 – кварце-

вый монцонит; 2 – кристалличе-

ский сланец; 3 – песок и гравий

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

218

Таблица 6.42. Матрица коэффициентов корреляции, собственные

значения, R- и Q-факторные нагрузки по данным состава и радио-

метрическим данным из Береа, штат Виргиния

Матрица коэффициентов корреляции порядка 44

ВР U Th К

BP 1,00

U 0,89

1,00

Th 0,82

0,89

1,00

K 0,82

0,67

0,69

1,00

Собственные значения

Факторы

I II III IV



3,39

0,39

0,15

0,06

% 84,81

9,76

3,87

1,55

, %

84,81

94,57

98,45

100,0

Нагрузки Q-метода

Факторы

I II III IV

BP 0,96

0,05

–0,22

–0,16

U 0,94

–0,27

–0,13

0,17

Th 0,92

–0,25

0,28

–0,07

K 0,86

0,51

0,09

0,07

Нагрузки Q-метода

Факторы

I II III IV

1 –0,75

0,12

–0,03

–0,01

2 –0,49

–0,02

0,03

3 –0,45

–0,02

–0,04

0,00

4 –0,41

0,04

–0,00

–0,08

5 –0,22

0,09

0,03

–0,05

6 0,11

0,29

–0,00

0,12

7 –0,08

–0,05

0,00

0,04

8 0,21

0,00

0,23

0,03

9 0,12

–0,08

0,02

–0,03

10 0,31

0,00

–0,01

–0,03

11 0,51

–0,23

0,00

–0,01

12 0,35

–0,18

–0,03

–0,09

13 0,53

0,14

–0,04

14 0,36

0,21

–0,11

–0,00

15 0,50

0,11

–0,08

–0,07

16 0,49

0,13

0,01

0,03

17 0,26

–0,09

–0,19

0,04

18 –0,40

–0,04

0,01

–0,00

19 –0,31

–0,11

0,15

0,01

20 –0,44

––0,03

–0,01

0,0

21 –0,41

–0,03

–0,05

–0,03

22 0,21

–0,26

–0,03

0,12

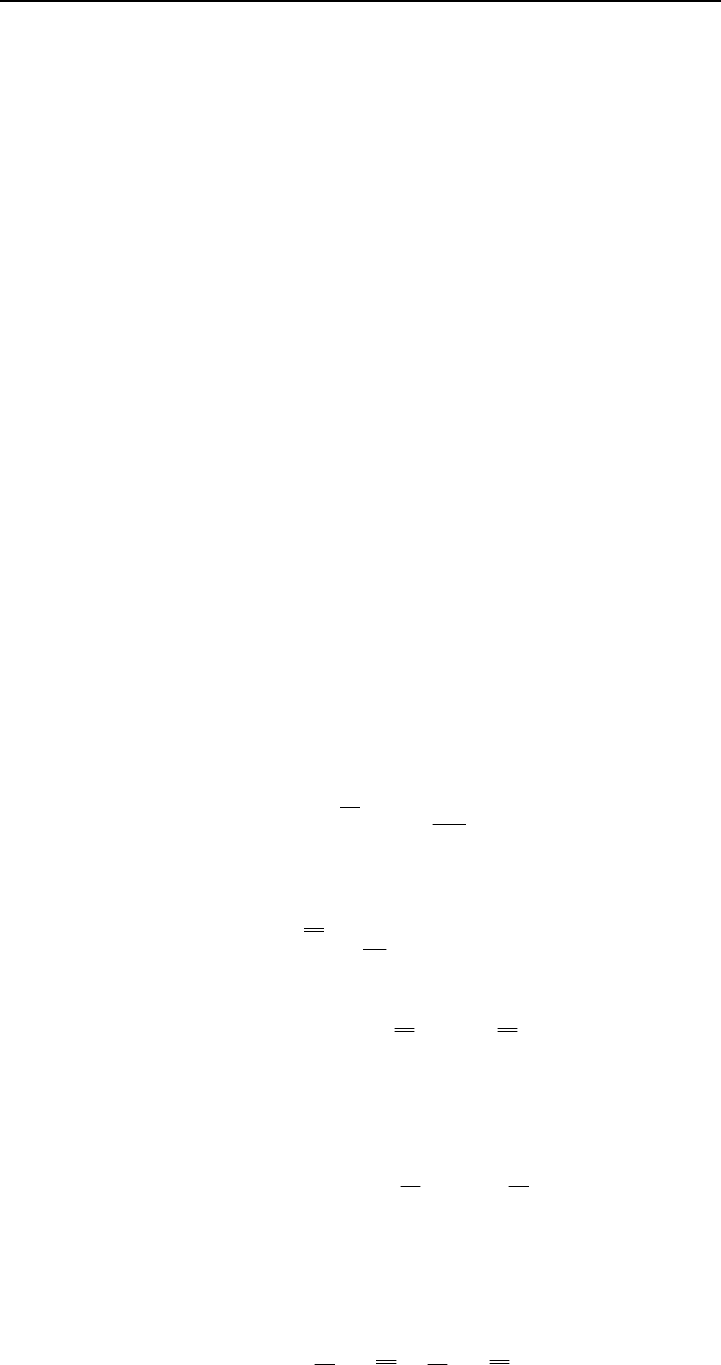
Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

219

МНОГОГРУППОВЫЕ ДИСКРИМИНАНТНЫЕ ФУНКЦИИ

Многогрупповой дискриминантный анализ вобрал в себя наиболее ценные черты дисперси-

онного анализа и связанные с ними вычислительные процедуры факторного анализа. Эта задача яв-

ляется обобщением уже рассмотренной процедуры дискриминантного анализа, связанной с разбие-

нием на две группы. В качестве примера рассмотрим задачу из палеонтологии, связанную с изуче-

нием полового диморфизма гастропод по образцам, взятым из нескольких различных мест. По мяг-

кой части их тел исследователь легко отличит самку от самца. Особи можно классифицировать как

самцы из совокупности A, самки из совокупности А, самцы из совокупности В и т.д. Многомерные

измерения, сделанные на раковинах, используются в дискриминантном анализе для нахождения

комбинаций измерений, которые позволяют различить как их пол, так и совокупности, из которых

они взяты. К счастью, различия пола оказываются более ярко выраженными, чем различия между

совокупностями. Этот метод дает возможность выделить характеристики раковин гастропод и клас-

сифицировать ископаемые останки раковин в соответствии с их полом.

Аналогия с дисперсионным анализом состоит в том, как дисперсии и ковариации разделяют-

ся на категории или группы. Вспомним, как в гл. 2 в одномерном дисперсионном анализе общая

сумма квадратов SS

равнялась сумме квадратов в каждой группе SS

плюс сумма квадратов между

группами SS

. Точно такая же структура удобна и в дискриминантном анализе.

Обозначения многогруппового дискриминантного анализа достаточно сложны, так как тре-

буется рассмотреть не только объекты и переменные, но и группы, в которых лежат эти объекты. В

силу этого нужно сначала использовать обозначения с тремя индексами, например, x

ijk

обозначает t-

ю переменную, измеренную на j-м объекте внутри группы k. Дело осложняется тем, что не все

группы содержат одинаковое число объектов, поэтому необходимо ввести обозначение для числа

объектов в k-й группе – n

. Предположим, что наблюдения классифицируются в g различных групп.

Если собрать все группы вместе, то мы найдем, что во всем множестве имеется всего





объектов, каждый из которых характеризуется некоторым набором переменных.

Среднее i-й переменной в k-й группе есть









ijk

(6.104)

Общее среднее i-й переменной есть среднее всех наблюдений переменной i, несмотря на группы, в

которых находятся наблюдения. Это общее среднее равно



 





ijk

1 1

(6.105)

Коэффициент ковариации между переменными i и l для всех объектов, несмотря на группы, равен



 





ijk

ijkij

XxXxs

1 1

))((

(6.106)

Если вычислить эту меру для всех возможных пар переменных, то получим симметрическую матри-

цу [S] порядка рр, которая будет называться матрицей общих сумм произведений. Вычислим так-

же меру ковариации между переменными i и l внутри g групп по формуле



 





ijk

ijkil

XxXxw

1 1

))((

(6.107)

Для всех возможных пар переменных эти коэффициенты образуют матрицу [W], которая

представляет сумму произведений между группами. Эта матрица эквивалентна сумме матриц [SPA]

и [SPB], используемых в простом дискриминантном анализе для двух групп. Наконец, выразим

дисперсию между группами:









ikliki

XXXXb

))(( (6.108)

Это также матрица [В] порядка рр, которая содержит межгрупповые суммы произведений.

Дж. С. Дэвис. Статистический анализ данных в геологии. Книга 2

220

Как и в обычном дисперсионном анализе, внутригрупповые и межгрупповые суммы квадра-

тов, сложенные вместе, дают общую сумму произведений

[S] = [B] + [W] (6.109)

Желательно, чтобы отношение [В]/[W] было по возможности велико. Легко убедиться, что это от-

ношение является многомерным аналогом отношения F, заданного по формуле F = МS

/МS

, ис-

пользуемого для проверки различия между группами в дисперсионном анализе. Если это отношение

велико, то это значит, что группы широко разбросаны, в то время как наблюдения внутри групп

плотно собраны вокруг своих средних.

Задача дискриминантного анализа состоит в нахождении множества линейных весов для пе-

ременных так, чтобы это отношение было максимальным. Если считать, что это множество весов

образует вектор [A

], то дискриминантный анализ можно трактовать как задачу нахождения элемен-

тов этого вектора [A

] таким образом, чтобы отношение

]][[][

AWA

ABA



достигало максимума. Конечно, на вектор [A

] необходимо наложить некоторые ограничения. В

дискриминантном анализе обычно накладывается следующее ограничение: знаменатель этого вы-

ражения должен быть равен единице, т.е. 1]][[][





AWA .

При выполнении этого условия отношение будет достигать максимума тогда, когда [A

] –

собственный вектор матрицы [W]

-1

[B] соответствует наибольшему собственному значению. Можно

найти второе множество линейных весов [A

], которые являются элементами собственного вектора,

соответствующего второму по величине собственному значению. Аналогично можно найти третье

множество весов, четвертое и т.д. Таким образом, мы вычислим последовательность дискриминант-

ных функций, которые дают разделение на заранее заданные группы настолько хорошо, насколько

это возможно. В силу природы собственных векторов они ортогональны друг другу, и каждый сле-

дующий является вектором, дающим наилучшее разделение. Можно вычислить дискриминантную

функцию для каждого положительного собственного значения. В общем случае число положитель-

ных собственных значений будет равно наименьшему из чисел g–1 или р. К сожалению, матрица,

полученная по формуле [W]

-1

[B], не является симметричной, и поэтому ее собственные векторы на-

ходятся нелегко. В некоторых программах дискриминантного анализа собственные векторы нахо-

дятся итерационными методами, основанными на процессе, называемом разложением на особые

значения [7]. Другие программы сначала преобразовывают матрицу в симметричную форму, а затем

находится множество собственных векторов, которое в свою очередь преобразуется в требуемое

множество. Этот метод описан в [19], критические шаги пояснены в [47].

Наблюдения, используемые в вычислении дискриминантной функции, можно спроектиро-

вать на пространство, определенное дискриминантными осями. Это делается с помощью матрично-

го умножения

][][ XAZ





(6.110)

где [X] – исходная матрица данных порядка Np; [A] – матрица порядка pt, столбцы которой со-

стоят из t собственных векторов, соответствующих наибольшим собственным значениям, которые

используются в дискриминантных функциях. Центроиды g групп можно спроектировать на дискри-

минантное пространство по формуле

][][][

XAZ



 (6.111)

где матрица [Х

] имеет порядок gp и состоит из средних всех переменных для каждой группы. Ог-

раничим свое внимание на парах дискриминантных функций (обычно это первая и вторая) и нане-

сем наблюдения и центроиды групп на диаграмму рассеяния. Обычно предварительно данные шка-

лируются. В некоторых программах производится стандартизация, а из каждого наблюдения вычи-

тается общее среднее и результат делится на стандартное отклонение, вычисленное по всему мно-

жеству данных. В других программах деление производится на объединенные внутригрупповые

стандартные отклонения. Мараскилло и Левин [46] дают поучительное сравнение различных подхо-

дов.

Очевидно, наблюдение неизвестного происхождения можно спроектировать на дискрими-

нантное пространство, просто умножая его слева на транспозицию матрицы [А]. Групповая принад-

лежность нового наблюдения становится очевидной из его положения на диаграмме рассеяния, од-