Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

SECTION 21.7 THE MEET AND JOIN OF BLADES 539

3. Compute the dual of the delta product: S = (AM B)

∗

. A threshold  may be used to

suppress ﬂoating-point noise when computing the delta product (speciﬁcally, when

determining what is the top grade part of ABthat is not zero).

4. Factorize S into factors s

5. Compute the required grade of the

meet and join ((21.5) and (21.6)).

6. Set M ← 1, J ← I

denotes the pseudoscalar of the total space).

7. For each of the factors s

(a) Compute the projection p

and rejection r

of s

and A:

= (s

A)A

−1

= s

− p

(b) If the projection is not zero, then wedge it to the meet: M ← M ∧ p

.Ifthe

new grade of M is the required grade of the

meet, then compute the join using

(21.7), and break the loop. Otherwise continue with s

i+1

join: J ← r

J. If the new

grade of J is the required grade of the

join, then compute the meet using

(21.8), and break the loop. Otherwise continue with s

i+1

8. Output: A ∩ B and A ∪ B.

For added efﬁciency, step 4 could be integrated into the main loop of the algorithm (i.e.,

only ﬁnd factors of S as required).

Note that the algorithm returns both A ∩ B and A ∪ B at the same time, while only one

of them may be required. However, benchmarks have shown that this algorithm is more

efﬁcient than an algorithm that searches speciﬁcally for either the

meet or the join,asit

will terminate as soon as it ﬁnds either of them. The returned

join and meet are based

on the same factorization, so we can use relationships of (21.7) and (21.8) to compute

one given the other.

The number of loop cycles in the algorithm is n−1 in the worst case, where n is the dimen-

sion of the vector space. This can be understood by analyzing the following worst-case

scenario,

A = e

, B = e

in which case

M B = 1, S = (A M B)

∗

= e

∧ e

∧···∧e

The algorithm w ill start by projecting and rejecting e

.Theprojectionwillbezero,sothe

M w ill not grow towards the actual

meet (likewise for e

···e

n−1

). When the projection

is zero, the rejection is obviously nonzero, so each of the rejections is removed from the

J. While this brings J closer and closer to the actual

join, J has to shrink all the way until

it is of grade 1, which will not happen until all e

···e

n−1

have been processed, leading to

O(n) cycles of the loop.

540 FUNDAMENTAL ALGORITHMS FOR NONLINEAR PRODUCTS CHAPTER 21

We should note, however, that when the inputs A and B are in general position, the

projection and rejection are likely to be nonzero in each cycle of the loop. In that case

the required number of cycles is min(grade(

meet),grade(join)) ≤ n/2. For numeri-

cal stability, we should require that the projections and rejections have some minimum

weight, which will increase the number of cycles (because some projections and rejections

will not be used for computation).

21.8 STRUCTURAL EXERCISES

1. For A = e

+ e

∧ e

, compute A

−1

, then verify that



−1

and AA

−1

indeed behave

differently under the test in the algorithm of Section 21.5.

2. Prove that f ≡ (cB)/B isafactorofB (if nonzero) so that B = f ∧ B

for some blade

. Give an expression for a possible B

(it is not unique).

SPECIALIZING THE

STRUCTURE FOR

EFFICIENCY

This chapter describes an approach to efﬁciently implementing geometric algebra. By

“efﬁcient” we mean that if you wr ite a program that uses geometric algebra to do some

geometry, it should be about as fast as a similar program that uses a traditional opti-

mized method to do the same geometry. For example, the homogeneous model in geo-

metric algebra (Chapter 11) should perform on par with a traditional implementation of

homogeneous coordinates in linear algebra. We will demonstrate that this is possible with

benchmarks of a ray tracer. The ray tracer itself is described in the next chapter.

We assume that you have read the preceding implementation chapters, as our goal here is

to implement efﬁciently what is described there. The approach we take is largely inde-

pendent of a speciﬁc programming language, as long as the language has some con-

cepts of object orientation (i.e., classes). Some examples of actual C++ code generated

Gaigen 2 are given to make the approach more tangible.

22.1 ISSUES IN EFFICIENT IMPLEMENTATION

By now, we hope we have convinced you that geometric algebra is a structured and elegant

mathematical framework for geometry. In computer science, better structure and g reater

elegance often help to simplify the implementation of problems and to avoid errors.

541

542 SPECIALIZING THE STRUCTURE FOR EFFICIENCY CHAPTER 22

However, when geometric algebra is ﬁrst presented to a computer scientist or

programmer, the question arises how an implementation of geometric algebra can ever

be as efﬁcient as the current way of implementing geometry (based in linear algebra with

various extensions). Many features of geometric algebra seem to work against efﬁciency:

coordinates are required to represent a multivector for an n-dimensional space, the

conformal model of 3-D space requires a 5-D algebra (with its 32-D basis), there appear

to be many products and operations, and so on.

All initial geomet ric algebra implementations (like [43, 47]) seemed to conﬁrm this, for

they were st ructurally pretty but unacceptably slow for practical applications on high vol-

ume data. They were not designed with efﬁciency in mind. This is a pity, for the structure

of geometric algebr a actually offers many opportunities to home in on the essential com-

putations that need to be done in an application. Effectively, these permit its practical use

as a high-level programming language that computes efﬁciently.

Three issues will recur in the attempt to make an efﬁcient implementation: multivectors,

metrics, and operations.

•

Multivectors are the fundamental elements of computation in geometric algebra,

but they are big (2

coordinates for n-D). So although it is mathematically attractive

that all elements can be considered as multivectors, you would rather not base an

implementation on it.

Fortunately, most geometrically sensible elements of computation use only limited

grades, and in a particular manner. This suggests deﬁning a ﬁxed, specialized multi-

vector type for a variable whenever possible, to reduce storage and processing. Such

a multivector type is an indication of its geometrical meaning, immediately imply-

ing a more limited use of grades or basis blades. Examples of specialized multivector

types in the programming examples of Part I and II abound:

vector, translator,

and

circle,tonameafew.

In a large group of geometric algorithms and applications, we can naturally im-

pose such ﬁxed multivector types on variables without compromising our solutions.

(And if in some application we cannot, we can always revert to the multivectors.)

•

The metric is a very fundamental feature of a geometric algebra, affecting the most

basic products. Many different metrics are useful and need to be allowed, yet looking

up the metric at run-time (e.g., from a table) is too costly. We should therefore not

just implement a general geometric algebra and use it in a particular situation; for

efﬁciency, we need a special implementation for every metrically different geometric

algebra.

•

The number of basic operations on multivectors is quite large, and e very opera-

tion can be applied on every element. Written out in coordinates, the operations

are not complicated, but precisely because the execution of each individual prod-

uct or operation requires relatively few computations, any overhead imposed by

the implementation (such as a conditional branch due to looping) will result in a

signiﬁcant degradation of performance.

SECTION 22.2 GENERATIVE PROGRAMMING 543

As a consequence, expressions consisting of multiple products and operations can

often be executed much more efﬁciently by folding them into one calculation, rather

than executing them one by one through a series of generic function calls.

This suggests programming things out explicitly for each operation and each multi-

vector type, with the danger of a combinatorial explosion in the volume of the code.

These considerations lead to the conclusion that for efﬁcient performance, the elegant

universal and unifying structure of geometr ic algebra needs to be broken up. Multivec-

tors are general but too big, metrics are unifying but too basic to be variables, and the

operations are simple and universal but too slow when not specialized and optimized.

Building such an optimized implementation of a particular geometric algebra is a lot of

administrative work. It may be possible to do it by hand in limited, low-dimensional cases,

but even then it is tedious and error-prone.

Fortunately, we do not need to do it ourselves. We should use the actual algebra to convert

its coordinate-free expressions into low-level, coordinate-based code that can be directly

executed by a processor. Used in that way, geometric algebra can be the engine of an auto-

matic code generator, which can take a high-level speciﬁcation of a solution for a geometric

problem and automatically generate efﬁcient implementations.

With such a tool, we never again have to write the error-prone, low-level code that directly

manipulates coordinates. Instead, we just w rite our algorithms in the high-level language,

conﬁdent that this will automatically lead to correct and efﬁcient code.

22.2 GENERATIVE PROGRAMMING

Generative programming [11] is the craft of developing programs that synthesize other

programs. One of its uses is to connect software components (such as algebra implemen-

tations) without loss of performance. Ideally, each component adapts dynamically to its

context. In our case, we would like to use generative programming to transform the spec-

iﬁcation of a geometric algebra into an optimized implementation that is tailored to the

needs of the rest of the program.

There are several points in the tool-chain (illustrated in Figure 22.1) from source code to

fully linked and running program where this transformation can take place. Here we list

three obvious examples, but other approaches (or hybrids) are also possible:

1. The most explicit approach is generating an implementation of the algebra before

the actual compilation of the program takes place. This is the way classical code gen-

erators like

lex and yacc work. Advantages are that generated code is directly avail-

able to the user as a library, and that this method does not cause interference with

the rest of the chain. The main disadvantage is that it does not integrate well, since

a separate program is required to generate the code. Another disadvantage is that

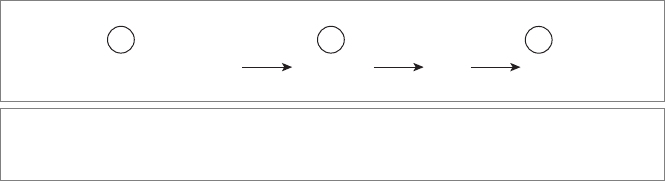
544 SPECIALIZING THE STRUCTURE FOR EFFICIENCY CHAPTER 22

Source code Compile Link Run

1 2

Figure 22.1: Basic tool-chain from source code to running application with three possible

points where code generation can take place (see text).

some form of feedback from the ﬁnal, running program (i.e., proﬁling) is required

to allow the implementation to adapt itself to the context, and this may require an

extra code generation pass. The geometric algebra implementations

Gaigen and

Gaigen 2 take this approach.

2. The transformation can also take place at compile-time, if the programming

language permits this. This is called meta-programming, where the algebra imple-

mentation is set up such that the compiler generates parts of it at compile time.

For example, in C++ this is possible through the use of the templates feature

that was originally added to the language for generic programming. The deﬁnite

advantage of this method is the good integr ation with the language. A disadvan-

tage is the limited number of mainstream programming languages that support

meta-programming. Disadvantages speciﬁc to the C++ programming language

are the complicated template syntax, hard-to-decipher compiler error messages

(for both user of the library and its developer), and the long compile times. The

boost::math::clifford library [61] uses this approach.

3. A third option is to delay code generation until the program is up and running. The

program would generate the code as soon as it is required (e.g., the ﬁrst time a func-

tion of the algebra is called with speciﬁc arguments). The advantages are that the

algebra implementation can adapt itself to the actual input and the actual hardware

that it runs on (e.g., available instruction set extensions, the speed of registers com-

pared to cache compared to main memory, etc. [5]). Disadvantages are the slower

startup time of the ﬁnal program (due to the run-time code generation) and the

fact that the method is rather nonconventional and hard to implement. At the time

of writing, we are not aware of such a geometric algebra implementation.

The geometric algebra implementation described below can in principle be realized

through each of these generative programming methods, so below we simply call it the

code generator, regardless of the precise details.

22.3 RESOLVING THE ISSUES

The overall goals of our implementation can be stated as follows:

1. Waste as little memory as possible (i.e., store each variable as compactly as possible).

SECTION 22.3 RESOLVING THE ISSUES 545

2. Implement functions over the algebra most efﬁciently. To do this you need several

things:

(a) Process as few zero coordinates as possible (which coincides with Goal 1),

(b) Minimize (unpredictable) memory access. This coincides w ith Goal 1 and

Goal 2a, but also demands avoiding lookup from tables, and so on.

tional branch, a large number of processor cycles is lost.

(d) Unroll loops (e.g., over the dimension of the algebra or the grade of a blade)

whenever possible. This avoid branches and also allows you to apply further

optimizations.

(e) Optimize nontrivial expressions. Avoid implementing them as a series of func-

tion calls.

When we hold our (purposely naive) reference implementation based on Chapters 19

to 21 up to this list of demands, we see that it violates all but one of them. It wastes mem-

or y due to the bookkeeping required for per-coordinate compression, looks up the metric

from tables, uses many conditional branches due to looping, does not unroll loops, and

processes operations one by one. The only thing that it does right is minimizing the pro-

cessing of zero coordinates.

22.3.1 THE APPROACH

Through generative programming, we can resolve each of the issues listed in Section 22.1

in a way that satisﬁes these goals. We ﬁrst sketch how the issues can be resolved, followed

by a more detailed description in the next section.

•

As we indicated, the problem that multivectors are too general can be resolved by

generating classes for speciﬁc multivector types. These classes store only the nonzero

coordinates for that speciﬁc type (e.g., the 3-D vector class only stores the e

-, e

and e

-coordinates, as all other coordinates are always 0). We can also generate

classes that represent useful constants (such as e

, I, and o ∧∞). These classes are

used mostly as symbolic tokens, as they will be optimized away when they are used in

expressions. The combination of these two ideas leads to a hybrid where only some

coordinates are constant. For example, the o-coordinate of a normalized homoge-

neous point is always 1.

•

Using generative programming, the metric of the algebr a can now be hard-coded

directly into the implementation by the code generator, taking very little effort from

the user. Likewise, the large implementation effort due to the combinatorial explo-

sion caused by the large number of products/operations and multivector types is no

longer an issue, as the code generator does the tedious work for us (note that not

every function should be generated for every combination of arguments, but only

those that are actually used by the program).

546 SPECIALIZING THE STRUCTURE FOR EFFICIENCY CHAPTER 22

•

Finally, by optimizing functions over the algebra, the code generator can fully

optimize equations consisting of multiple products and operations, because it can

oversee the whole context.

The approach is built on top of Chapters 19 and 20. First, it can be seen as an optimization

of the list of basis blades approach from Section 20.2. The optimization is to generate a

separate class for each type of list (i.e., multivector type) that we expect to encounter in

our program, thus avoiding the need for explicit bookkeeping of the list. Second, to write

out expressions (involving products and operations) on a basis, we need Chapter 19. The

nonlinear functions from Chapter 21 are not essential to the approach, but most of them

are suitable candidates for optimization, as described in Section 22.4.6.

22.4 IMPLEMENTATION

We now describe the implementation in some more detail, starting with the speciﬁca-

tion of the algebra, followed by a description of the classes and functions that should be

generated.

22.4.1 ALGEBRA SPECIFICATION

The speciﬁcation of the algebr a is the starting point for the code generator. It speciﬁes at

least the following:

•

The dimension of the algebra;

•

The metric of the algebra;

•

Deﬁnition of the specialized types;

•

Deﬁnition of constants.

We brieﬂy discuss these terms before moving on to their implementation.

Dimension of the Algebra

The geometric algebra of R

has the dimensionalit y n, which should be speciﬁed. Within

it is convenient to specify a basis (not necessarily orthonormal; see below). Since geo-

metric algebra is too new to have a standardized notation, it is sensible to permit the user

to choose the names of the basis vectors. This results in more readable code, and output

in a recognizable format.

Metric

The metric should allow for a nondiagonal metric matrix, even though an equivalent

metric with a diagonal metric matrix always exists. The reason for this is that in certain

models, it may be more intuitive and efﬁcient to deﬁne the metric in an off-diagonal

manner. For example, in the conformal model of Euclidean geometry, ∞ and o are more

fundamental than the vectors e and

e (see (13.5) for the relationships of these bases.

SECTION 22.4 IMPLEMENTATION 547

The increased efﬁciency of this basis is obvious when we write out the coordinates of

a conformal line A relative to each basis. Using the o,∞-basis we get

A = A

1o∞

+ A

2o∞

+ A

3o∞

12∞

+ A

13∞

+ A

23∞

while the e,

e-basis results in

A = A

+ A

− A

12e

+ A

− A

13e

+ A

− A

23e

(here we use shorthand to denote the coordinates A

...

and the basis elements e

...

, i.e.,

13∞

= e

∧ e

∞

, etc.). So, storing a line requires six coordinates on the o,∞-basis

compared to nine coordinates on the e,

e-basis, three of which are duplicates (A

= A

12e

= A

13e

, and A

= A

23e

Specialized Types

The deﬁnition of each specialized type should list the basis blades required to represent it.

The deﬁnition could also include whether the type is a blade or a versor, so that run-time

checks can be made (e.g., in debug mode) to verify the validity of the value.

Preferably, the deﬁnitions should also allow certain coordinates to be deﬁned as constant.

For example, a normalized point has a constant o-coordinate, so there is no need to store

it. It may also be useful to have the ability to specify the order in which coordinates are

stored. This can simplify and optimize connections to other libr aries, which may expect

coordinates to be in a certain order.

Specialized types for matrix representations of outermorphisms are also an option. For

example, in connection with OpenGL it is useful to have a special type to contain the

outermorphism matrix representation that can be applied directly to a grade 1 blade (a

4×4 matrix). In our programming examples, we have used such a type in Sections 11.13.2,

12.5.1, and 13.10.3.

Constants

Important constant multivector values inside a program can be encoded as constants.

Examples are basis vectors such as e

and o or the pseudoscalar I. We should include the

constants in the algebra speciﬁcation and generate special types for them, in such a way

that their use in expressions can be optimized away by the code generator or the compiler.

22.4.2 IMPLEMENTATION OF THE GENERAL

MULTIVECTOR CLASS

In our approach, an implementation of the general (nonspecialized) multivector is

always required. The specialized types approach works best when the multivector ty pe

548 SPECIALIZING THE STRUCTURE FOR EFFICIENCY CHAPTER 22

of each variable in a program is ﬁxed. This assumption often holds, but also cripples

one of the amazing abilities of geometric algebra: many equations work regardless of

the multivector type of their input. For some programs (e.g., those dealing with noisy

input or interactive input), the multivector type of variables may change at run-time.

This prevents the use of specialized multivector types at compile-time, and hence for

such programs we should provide a fallback option that may not be efﬁcient, but at

least works.

Coordinate Compression

An important issue when implementing the general multivector class is compression of

the coordinates. The coordinates of the gener al multivector could be stored naively (all

of them), but to increase performance, compression can be used to proﬁt from the

inherent sparseness of geometric algebra. By compression, we mean reducing the number

of zero coordinates that are stored.

•

Per-Coordinate Compression. The most straightforward compression method is

per-coordinate compression. Each coordinate is tagged with the basis blade it refers

to, and the coordinates are stored in a list. Zero coordinates are not stored in this

list. We already encountered this type of compression in Section 20.2.

•

Per-Grade Compression. Multivectors are typically sparse in a per-grade fashion:

blades, by deﬁnition, have only one nonzero grade part. Likewise, versors are either

even or odd, implying that at least half their grade parts are null. This suggests

grouping coordinates that belong to the same grade part: when a grade part is not

used by a multivector, the entire group of coordinates for that grade is not stored.

Instead of signaling the presence of each individual coordinate, we signal the pres-

ence of the entire group.

For low-dimensional spaces, per-grade compression is a good balance between per-

coordinate compression and no compression at all. Per-coordinate compression is

slow b ecause each coordinate has to be processed individually, leading to excessive

conditional branching, which slows down modern processors. No compression at

all is slow because lots of zero coordinates are processed needlessly. Per-grade com-

pression reduces the number of zero coordinates while still allowing sizable groups

of coordinates to be processed without conditional branching.

•

Per-Group Compression. Per-grade compression does miss some signiﬁcant com-

pression opportunities. For example, a ﬂat point in the conformal model (a 2-blade)

requires only four coordinates, while the grade 2 part of 5-D multivectors requires

10 coordinates in general. Thus per-grade compression stores at least six zero coor-

dinates for each ﬂat point. As the dimension and structure of the algebra increases,

this storage of zero coordinates becomes more of an issue. A more reﬁned grouping

method may alleviate this problem, but what the groups are depends heavily on

the speciﬁc use of the algebra. For example, in the conformal model for Euclidean

geometry, one could group coordinates based on the presence of ∞ in the basis