Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

SECTION 2.3 ORIENTED AREA ELEMENTS 27

a + b

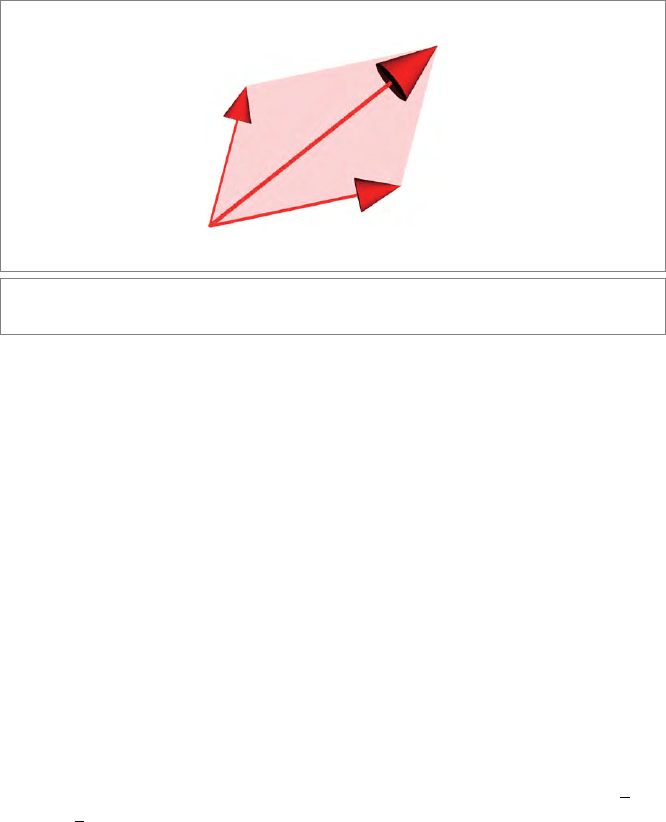
Figure 2.2: Imagining vector addition.

to generate the ﬁgures. But you should think and feel that vector addition is geometric: it

completes the parallelogram of a and b, and algebraically there is no need to go lower than

the notation a+ b, which has all the properties you need. After you have loaded Figure 2.2

GAViewer, you can drag a and b, and see the resulting change in a + b, in 3-D. That

conveys precisely this coordinate-free feeling. Playing with this and the other ﬁgures will

aid your intuition. It will help you dare to leave coordinates behind, and think about the

algebra at the proper level of geometric primitives.

2.3 ORIENTED AREA ELEMENTS

2.3.1 PROPERTIES OF PLANES

A plane through the origin is a 2-D homogeneous subspace of the vector space R

.Itmay

be determined by two linearly independent vectors, a and b, in the sense that any vector

x in the plane can be written as

x = λa + μb.

This speciﬁcation is not unique. For instance, replacing a and b by (a + b)/

√

2 and

(a − b)/

√

2 gives the same set of vectors, as do many other linear combinations on a and

b. We should think about replacing the speciﬁcation with something more appropriate,

which will make it easier to verify whether two speciﬁcations refer to the same plane.

Moreover, just like the homogeneous line, a homogeneous plane has more properties than

just being a set of vectors. We list those properties, illustrated in Figure 2.1(c):

•

A homogeneous plane has an att itude in the surrounding n-dimensional space

. This is its “subspace aspect” of being a par ticular planar carrier. In 3-D, this

is the property traditionally characterized by a normal vector for the plane, with

28 SPANNING ORIENTED SUBSPACES CHAPTER 2

any weight or orientation. But such a characterization by a vector is insufﬁcient for

a planar subspace of an n-dimensional space. (Another defect is that it character-

izes the nonmetric concept of a particular 2-D subspace by a metric construction

involving perpendicularity.)

•

A plane may be considered to have an orientation, in the sense that the plane

determined by two vectors a and b would have the opposite orientation of a plane

determined by the vectors b and a. We use this often when we specify angles, speak-

ing of the angle from a to b as being of opposite sign to the angle from b to a.The

sign of the angle should be referred to more properly as relative to the orientation

of the plane in which its deﬁning vectors reside.

•

A plane has a measure of area, which we shall call its weight. The plane determined by

the vectors 2a and b has twice the weight (or double the area measure) of the plane

determined by the vectors a and b. As with vectors, this weight is for now only a

relative measure within planes of the same attitude. (We would need a metric to

compare areas within different planes.)

In linear algebra, the orientation and the area measure are both well represented by the

determinant of a matrix made of the two spanning vectors a and b of the plane: the ori-

entation is its sign, the area measure its weight (both relative to orientation and area mea-

sure of the basis used to specify the coordinates of a and b). In 2-D, this speciﬁes an area

element of the plane. In 3-D, such an area element would be incomplete without a speciﬁ-

cation of the attitude of the plane in which it resides. Of course we would prefer to have a

single algebraic element that contains all this geometric information about the plane.

2.3.2 INTRODUCING THE OUTER PRODUCT

We now introduce a product between vectors to aid in the speciﬁcation of the plane con-

taining the two vectors a and b. Its deﬁnition should allow us to retrieve all geometrical

properties of the plane. We denote this algebraic product by a ∧ b.

The algebraic consequence of our geometrical desire to give the plane an orientation is

that a∧b should be opposite in sign to b∧a, so that a∧b = −b∧a. When b coincides with

a, this would give the somewhat unusual algebraic result a ∧a = −a∧a. This suggests that

the square of a, using this product, must be zero. Geometrically, this is very reasonable:

the vector a does not span a planar element with itself, and we may encode that as a planar

element with weight zero.

When we decrease the angle between a and b, the area spanned by a and b gets smaller as

they become more parallel. In fact, in a space with a Euclidean metric you would expect

the measure of area associated with the planar element a ∧ b to be ab sin ␾, with

␾ the angle between them. However, we should not make such an explicit property part

of the deﬁnition of a ∧ b—it involves just too many extraneous concepts like norm and

2 We use “span” here informally, and different from the use in some linear algebra texts, where the span of two

identical vectors would still be their common 1-D subspace rather than zero. That span is not very well-behaved;

it is not even linear. In Chapter 5, its geometry will be encoded by the

join product.

SECTION 2.3 ORIENTED AREA ELEMENTS 29

angle, which are moreover intrinsically metr ic. Instead, we try to deﬁne the product so

that this metric area formula is a consequence of more basic axioms. We note that the area

measure increases linearly in the magnitude of each of the vector factors of the product.

So let us at least make the product bilinear, giving it proper scaling and distributivity

relative to the constituent vectors.

Bilinearity and antisy mmetry are already enough to deﬁne the product a ∧ b completely.

We call the result the outer product of a and b. In view of the above, its deﬁning proper-

ties are:

Antisymmetry: a ∧ b = −b ∧ a

Scaling: a ∧ (β b) = β (a ∧ b)

Distributivity : a ∧ (b + c) = (a ∧ b) + (a ∧ c)

We pronounce a ∧ b as “a wedge b.” The outcome of the outer product a ∧ b of two

vectors is called a bivector or, more properly, 2-blade (we explain the difference between

these terms in Section 2.9.3). It is an element of the algebra we are developing that is

different from the scalars and vectors we have seen so far. Since the outer product is linear,

its outcomes are elements of a linear space, the “bivector space.” If we denote that space



, the outer product is a mapping ∧ : R

× R

→



You may think of a∧b as the span of a and b, in a quantitative manner, or as an oriented area

element of a particular homogeneous plane. Let us verify that that geometric interpretation

is indeed consistent with its algebraic properties. If we take a basis {e

} in the subspace

with the same attitude as a ∧ b, we can write a = a

+ a

and b = b

+ b

Then, using the deﬁnition, we develop the outer product to a recognizable form:

a ∧ b = (a

+ a

) ∧ (b

+ b

)

= a

∧ e

+ a

∧ e

+ a

∧ e

+ a

∧ e

= (a

− a

) e

∧ e

(2.2)

since the antisymmetry implies that e

∧ e

= −e

∧ e

,soitmustbeequalto0—as is

any outer product of parallel vectors.

We can write the ﬁnal result in terms of a determinant by introducing the matrix [[ ab]]

with, as its columns, the coefﬁcients of a and b on the {e

}-basis. This yields

a ∧ b = det([[ab]] ) e

∧ e

This determinant you know from linear algebra as a relative measure for the oriented

area spanned by a and b relative to the area spanned by the basis vectors e

and e

.Its

value is what we called the relative weight of a plane element. The other part of the result,

∧ e

, can then be consistently interpreted as the geometrical unit in which area in this

plane is measured (i.e., the amount of standard area with the correct attitude, in the plane

spanned by the basis vectors e

and e

). The orientation of the plane, and hence the relative

orientation of a ∧ b, is speciﬁed by the order of e

and e

30 SPANNING ORIENTED SUBSPACES CHAPTER 2

The outcome of a ∧ b neatly contains all three geomet ric properties in one algebr aic

element of computation, as we had hoped. If you want to see what happens when you

have a Euclidean metric in the plane, do structural exercise 1.

In summary, we have the following algebraic representation of the geometry of homoge-

neous planes:

a ∧ b is a weighted, oriented area element of the 2-D subspace spanned by a and b

(or other vectors producing the same attitude)

(see Figure 2.1(c), which also denotes a piece of the inﬁnite homogeneous plane of which

a ∧ b is a part). This element a ∧ b maybecomezerowhena and b are parallel, or when

either vector has zero norm, in agreement with our geometrical intuition that no planar

element is spanned in those cases.

When we have multiple area elements in different planes in space, we cannot choose inde-

pendent bases for each of them. Yet it is still possible to decompose a ∧ b on a bivector

basis for the whole space. We demonstrate this in a 3-D space

with a totally arbi-

trary basis {e

} (not necessarily orthonormal). Let the coefﬁcients of a and b on

this basis be a

and b

, respectively. Then we compute, using the deﬁnition of the outer

product:

a ∧ b = (a

+ a

) ∧ (b

+ b

)

= a

∧ e

) + a

∧ e

) + a

∧ e

) +

∧ e

) + a

∧ e

) + a

∧ e

) +

∧ e

) + a

∧ e

) + a

∧ e

)

(2.3)

= (a

− a

) e

∧ e

+ (a

− a

) e

∧ e

+ (a

− a

) e

∧ e

This cannot be simpliﬁed further. We see that an outer product of two vectors in 3-D

space can be written as a scalar-weighted sum of three standard elements e

∧ e

, e

∧ e

. Their weighting coefﬁcients are obviously 2-D determinants, which we know

represent directed area measures, now of the components of the original plane on the

coordinate planes of the basis. The formula is then consistent with the interpretation

of these three elements as standard area elements for the coordinate planes of the basis

vectors.

It is a pleasant surprise that area elements in 3-D have such a decomposable struc-

ture as a weig hted sum over a basis. Mathematically, this means that they reside

in their own bivector space of



, of three dimensions, with basis elements

≡ e

∧ e

, e

≡ e

∧ e

, e

≡ e

∧ e

3 This bivector space satisﬁes the mathematical axioms of a vector space, but it would be geometrically confusing

to call its elements vectors. We will reserve the term vector exclusively for the elements of

SECTION 2.3 ORIENTED AREA ELEMENTS 31

Any area element of the form a ∧ b can be decomposed onto a basis of standard

area elements.

In 3-D space, the converse also holds: a weighted sum of basis 2-blades is an area element

that can be factorized by the outer product in the form a ∧ b. But that property does

not hold in n-dimensional space; you cannot in general make factorizable 2-blades of the

form a ∧ b simply by adding basis bivectors w ith arbitrary weights. We get back to this

important issue in Section 2.9.

With the outer product, we can generate additional structure from our initial 3-D vector

space

and its real scalars R. You already know from linear algebra that determinants

of 2 × 2 matrices with 2-D vectors as columns are scalar areas, and that determinants of

3 × 3 matrices of 3-D vectors are scalar volumes; now we also have 2-D-oriented areas

spanned by 3-D vectors as a 3-D linear space of 2-D determinants. Subspaces and their

measures are beginning to fall into a new pattern.

2.3.3 VISUALIZING BIVECTORS

The algebraic properties of a bivector in 3-D are equivalent to those of a directed area

element. It is good to get a mental picture of such area elements, and of their interac-

tion using addition, that stays close to their algebraic properties. This will help us to “see”

bivectors in problems and their solutions.

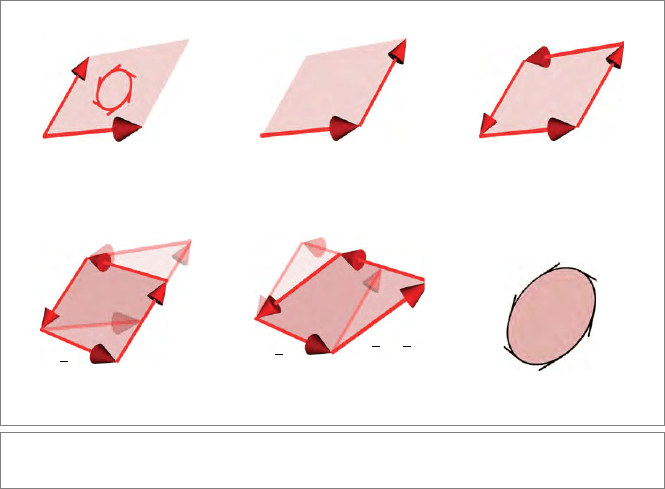
A ﬁrst attempt might be Figure 2.3(a): a∧b as the parallelogram spanned by a and b. Since

that does not convey the orientation (it looks commutative rather than anticommutative),

we need to denote this orientation by something extra, such as by the oriented circular

arc inside. We could also use a representation like Figure 2.3(b), in which the orientation

follows naturally from the order of the arrows. We can extend this to show some more of

the anticommutativity of the construction, which implies a ∧b = (−b ∧ a) = b ∧ (−a) =

(−a) ∧(−b) by showing all of those four vectors along the border, as in Figure 2.3(c). This

shows that none of the vertices of the parallelog ram can be seen as an anchor. Therefore

the depiction of the bivector is free to move translationally within its carrier plane, thoug h

we will prefer drawing it near the origin. Also, since a ∧ a = 0, we have to remember that

drawing the corresponding parallelogram is equivalent to drawing nothing at all, r ather

than some ﬂattened shape.

Not only can we imagine sliding the bivector out of the origin, but we can also reshape it in

some ways without changing its algebraic value. Anticommutativity of the outer product

implies, for instance, that (a −

b) ∧ b = a ∧ b = (a −

b) ∧ (

a +

b). Therefore, we

are allowed to reshape the parallelogram geomet rically by sliding the arrows along any

of its parallel sides (Figure 2.3(d, e)), obtaining another faithful depiction of the same

bivector a ∧b. If you have a coordinate system, there may be an advantage to redrawing the

bivector to have sides to be alig ned with the coordinate vectors. But you should realize that

there is no unique way of doing this; since a∧b = (2a) ∧(b/2) , and so on, the magnitudes

of the components are adjustable (as long as area and orientation remain the same).

32 SPANNING ORIENTED SUBSPACES CHAPTER 2

a ∧ b

−b

−a

a ∧ b

a ∧

a ∧ b

a −

a ∧ b

(a) (b) (c)

(d) (e) (f)

Figure 2.3: Bivector representations.

In fact, as soon as we have computed a bivector quantity, we have lost the identity of the

vectors that generated it. We may therefore prefer to denote it by a circular area in the

plane, as in Figure 2.3(f) (as long as we realize that even this circular shape is arbitrary).

We cannot emphasize enough that these redrawings all represent the same element. The

algebraic bivector is not speciﬁc on shape; geometrically, it is an amount of oriented area

in a speciﬁc plane, that’s all. Initially, this may appear too vague to be useful; but we will

soon see that this “reshapeability” is a strength, not a weakness.

2.3.4 VISUALIZING BIVECTOR ADDITION

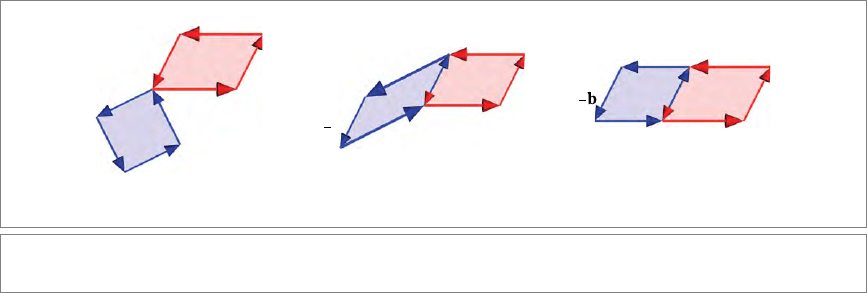
We can also make a geometrical representation of bivector addition. In the same plane,

addition of bivectors can be done by reshaping them until they can be added visually,

preserving both magnitude and orientation of their area during the reshaping, (see Fig-

ure 2.4). To add c ∧d to a∧b (assumed to be in the same plane!), ﬁrst reshape c∧d to be of

the form (γc) ∧( −b); see Figure 2.4(b). Place them side to side so that the (−b) side of the

ﬁrst bivector matches the b side of the second. Then reshape the area again, so that c ∧ d

is ﬁnally of the form αa ∧ b, as in Figure 2.4(c). Now the result is obviously (1 + α)a ∧ b.

But of course, you could change the order of the arguments and do not really need to do

the reshaping at all. It is just a matter of putting oriented areas together and algebraically

it is handled automatically by adding their coefﬁcients relative to a bivector basis.

SECTION 2.4 ORIENTED VOLUME ELEMENTS 33

a∧b

c∧d

a ∧ b

c ∧ d

γc

a ∧ b

∧ d

aαa

(a) (b) (c)

Figure 2.4: Imagining bivector addition in 2-D space.

Now consider the addition of two bivectors in R

. In 3-D space, two homogeneous planes

intersect in at least a homogeneous line, so two bivectors must have some vector in com-

mon. Calling this vector e, we can then reshape the two addends to have e asafactor.

Then they are both aligned with e, and the bivector addition reduces to vector addition.

For example, we compute (3e

∧e

)+ (e

∧e

) (as illustrated in Figure 2.5(a)) by factoring

out e = e

and adding 3e

and e

(Figure 2.5(b)). You have to be a bit careful, since you

may have to change the sign of one of the vectors before adding (Figures 2.5(c, d)) due to

the antisymmetry of the outer product.

In higher-dimensional spaces, this geometric construction is likely to fail, since in general

you will not be able to ﬁnd a common 1-D direction for two planes. Algebraically this

corresponds to the fact that not all bivectors can be factored as the outer product of two

vectors; we call the ones that can 2-blades. The algebraic difference between bivectors and

2-blades will be treated in detail in Section 2.9.3.

2.4 ORIENTED VOLUME ELEMENTS

2.4.1 PROPERTIES OF VOLUMES

We now consider representations of oriented volumes. By analogy with homogeneous

lines and planes, volumes can be treated as 3-D homogeneous subspaces of a vector space

. They have the geometric properties we found for lines and planes, illustrated by anal-

ogy in Figure 2.1(d).

•

Although it is somewhat hard to visualize for us 3-D beings, volumes have an atti-

tude in spaces of more than three dimensions, denoting the 3-D subspace that con-

tains them. In a 3-D space there is, of course, only one choice—all volumes are

proportional to the volume of the unit cube.

34 SPANNING ORIENTED SUBSPACES CHAPTER 2

∧ e

∧ 3e

∧ e

(a)

(b)

(c)

−3e

∧ e

(−3e

+ e

) ∧ e

∧ e

−3e

(d)

(3e

+ e

) ∧ e

Figure 2.5: Bivector addition in 3-D space: orientation matters. (a),(b): (3e

∧ e

)

+ (e

∧ e

) = (3e

+ e

) ∧ e

; (c),(d): (e

∧ 3e

) + (e

∧ e

) = (−3e

+ e

) ∧ e

, which is a different

bivector.

SECTION 2.4 ORIENTED VOLUME ELEMENTS 35

•

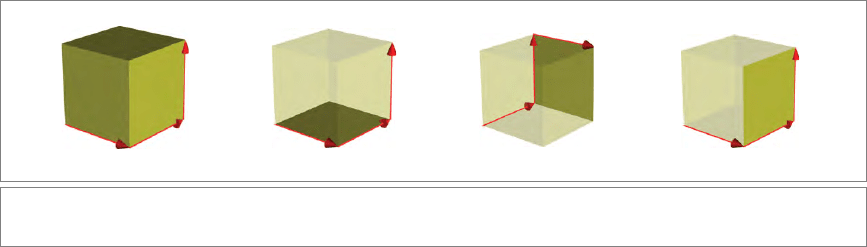
The volume has an orientation, usually referred to as handedness. In the 3-D space

of our example, the volume spanned by e

, e

(in that order), has opposite orien-

tation from that spanned by e

, e

, −e

(in that order); use a mirror in the (e

∧e

)

plane to see this. The latter has the same orientation as the volume spanned by

, e

(in that order—use two more mirrors), and of any odd permutation of

, e

). Orientation of volumes is thus an antisymmetric propert y, and there-

fore there exist only two different orientations (a glove can be right-handed or left-

handed—that’s all).

•

Volume has a scalar weight. It is well known from linear algebra that in 3-D space the

signed magnitude of the volume spanned by a, b, and c is proportional to the deter-

minant of the coefﬁcient matrix [[ abc]] with a, b, and c as columns. It is therefore

an antisymmetric linear function of the vectors.

We should try to ﬁnd an algebraic product to represent these geometric properties of

volumes.

2.4.2 ASSOCIATIVITY OF THE OUTER PRODUCT

The antisymmetry we signaled in the classical characterization of volume measures is a

clue to its representation in our new algebra. We simply attempt to extend the “span”

operation of the outer product to more than two terms. Algebraically, the most natural

way is to deﬁne the outer product to be associative:

associativity: (a ∧ b) ∧ c = a ∧ (b ∧ c).

We can thus write the volume element as a ∧b ∧c without ambiguity. (You should realize

that the outer product is still pairwise antisymmetric, so that a ∧ b ∧ c = −a ∧ c ∧ b =

c ∧ a ∧ b, etc.) Geometrically, this property would imply that we can span the same

oriented volume in different ways as the span of a planar element and a vector; if that were

not true, this algebraic formalization would be inappropriate. Fortunately, Figure 2.6 con-

ﬁrms the geometric validity of the algebraic associativity. It visualizes the volume a ∧b ∧c

in several equivalent ways, all leading to the same oriented amount of 3-space.

===b

(a ∧ b)∧ c

b ∧ (c ∧ a)

a ∧ (b ∧ c)

Figure 2.6: The associativity of the outer product.

36 SPANNING ORIENTED SUBSPACES CHAPTER 2

We call the element formed as the outer product of three vectors a trivector or 3-blade (the

difference is explained in Section 2.9.3). To verify its interpretation, we may int roduce

an arbitrary basis {e

, e

} in R

. Then the deﬁning properties of the outer product

yield

a ∧ b ∧ c =

= (a

+ a

) ∧ (b

+ b

) ∧ (c

+ c

)

(2.4)

= (a

− a

+ a

− a

+ a

− a

) e

∧ e

Therefore, any trivector in space

is a multiple of the trivector e

∧ e

. The pro-

portionality is the determinant of the spanning vectors on the basis {e

, e

},whichwe

recognize as the (relative) volume and its sign as the orientation relative to e

∧e

.In

linear algebra, we would write that scalar as the determinant det([[abc]] ) of the matrix,

with a, b, and c as columns. So the properties of a volume in the 3-D space

may

be characterized by a scalar, at least if we have agreed upon some convention about the

order of the basis elements (i.e., a handedness of the basis). That is indeed how it is done

classically.

In subtle difference, our algebra of the outer product permits us to treat a volume ele-

ment as a single trivector. This is tidier, since it requires no bookkeeping of an extraneous

convention: as the handedness of the basis changes, the trivector coefﬁcient automatically

changes its orientation appropriately. It is also clearly different from a scalar, even in 3-D

space, because it has the geometrical unit volume as part of its value. We can therefore

clearly express what happens when that is chosen differently (for instance, with a left-

handed rather than right-handed orientation). Moreover, this representation of volume

elements as the outer product of three vectors carries over unchanged to spaces of arbi-

trary dimensionality, and those will be surprisingly important, even for computations on

3-D space.

2.4.3 VISUALIZATION OF TRIVECTORS

In our geometric veriﬁcation of associativity, we met the obvious v isualization of a 3-blade

a ∧ b ∧ c in Figure 2.6, relating it to its vector factors a, b, and c.

Of course, this amount of oriented volume may be sheared (similar to what we did to

bivectors) as long as you do not change magnitude or orientation. If you have a basis, it is

sometimes convenient to align it with the basis vectors. If there are no vectors available,

just a trivector, you could draw it as a spherical volume, with some convention on how to

denote its orientation.

, the algebraic addition of trivectors is just a matter of adding their signed scalar

magnitudes. Since that has no aspects of geometrical attitude, explicit visualization of

trivector addition in 3-D is not really useful.